Selamat datang di salah satu kuliah di CS231n: Jaringan Syaraf Konvolusional untuk Pengenalan Visual .

Isi

• Tinjauan Arsitektur
• Lapisan dalam jaringan saraf convolutional
  - lapisan konvolusional
  - Lapisan subsampling
  - Lapisan normalisasi
  - Lapisan yang terhubung sepenuhnya
  - Konversi lapisan yang terhubung sepenuhnya ke lapisan convolutional
• Arsitektur Jaringan Syaraf Konvolusional
  - Lapisan template
  - Pola ukuran layer
  - Studi Kasus (LeNet, AlexNet, ZFNet, GoogLeNet, VGGNet)
  - Aspek komputasi
• Bacaan lebih lanjut

Jaringan Syaraf Tiruan Convolutional (CNN / ConvNets)

Jaringan saraf konvolusional sangat mirip dengan jaringan saraf biasa yang kami pelajari pada bab terakhir (merujuk pada bab terakhir dari kursus CS231n): mereka terdiri dari neuron, yang, pada gilirannya, berisi bobot dan perpindahan variabel. Setiap neuron menerima beberapa data input, menghitung produk skalar dan, secara opsional, menggunakan fungsi aktivasi nonlinear. Seluruh jaringan, seperti sebelumnya, adalah satu-satunya fungsi evaluasi yang dapat dibedakan: dari set piksel awal (gambar) di satu ujung ke distribusi probabilitas milik kelas tertentu di ujung lainnya. Jaringan ini masih memiliki fungsi kehilangan (misalnya, SVM / Softmax) pada lapisan terakhir (terhubung penuh), dan semua tips dan rekomendasi yang diberikan pada bab sebelumnya mengenai jaringan saraf biasa juga relevan untuk jaringan saraf convolutional.

Jadi apa yang telah berubah? Arsitektur jaringan saraf convolutional secara eksplisit melibatkan memperoleh gambar pada input, yang memungkinkan kita untuk mempertimbangkan sifat-sifat tertentu dari data input dalam arsitektur jaringan itu sendiri. Properti ini memungkinkan Anda untuk mengimplementasikan fungsi distribusi langsung secara lebih efisien dan sangat mengurangi jumlah parameter dalam jaringan.

Tinjauan Arsitektur

Kami mengingat jaringan saraf biasa. Seperti yang kita lihat pada bab sebelumnya, jaringan saraf menerima data input (satu vektor) dan mengubahnya dengan "mendorong" melalui serangkaian lapisan tersembunyi . Setiap lapisan tersembunyi terdiri dari sejumlah neuron tertentu, yang masing-masing terhubung ke semua neuron dari lapisan sebelumnya dan di mana neuron pada setiap lapisan sepenuhnya independen dari neuron lain pada tingkat yang sama. Lapisan yang terhubung sepenuhnya terakhir disebut "lapisan keluaran" dan dalam masalah klasifikasi adalah distribusi nilai berdasarkan kelas.

Jaringan saraf konvensional tidak dapat melakukan skala dengan baik untuk gambar yang lebih besar . Dalam set data CIFAR-10, gambar berukuran 32x32x3 (tinggi 32 piksel, lebar 32 piksel, 3 saluran warna). Untuk memproses gambar seperti itu, neuron yang terhubung penuh di lapisan tersembunyi pertama dari jaringan saraf normal akan memiliki bobot 32x32x3 = 3072. Jumlah ini masih dapat diterima, tetapi menjadi jelas bahwa struktur seperti itu tidak akan bekerja dengan gambar yang lebih besar. Sebagai contoh, gambar yang lebih besar - 200x200x3, akan menyebabkan jumlah bobot menjadi 200x200x3 = 120.000. Selain itu, kita akan membutuhkan lebih dari satu neuron tersebut, sehingga jumlah total bobot dengan cepat akan mulai tumbuh. Menjadi jelas bahwa konektivitasnya berlebihan dan sejumlah besar parameter akan dengan cepat mengarahkan jaringan ke pelatihan ulang.

Representasi 3D neuron . Jaringan saraf convolutional menggunakan fakta bahwa data input adalah gambar, sehingga membentuk arsitektur yang lebih sensitif untuk tipe data ini. Secara khusus, tidak seperti jaringan saraf biasa, lapisan dalam jaringan saraf convolutional mengatur neuron dalam 3 dimensi - lebar, tinggi, kedalaman ( Catatan : kata "kedalaman" mengacu pada dimensi ke-3 dari neuron aktivasi, dan bukan kedalaman jaringan saraf itu sendiri diukur dalam jumlah layer). Misalnya, gambar input dari dataset CIFAR-10 adalah data input dalam representasi 3D, dimensi yang 32x32x3 (lebar, tinggi, kedalaman). Seperti yang akan kita lihat nanti, neuron dalam satu lapisan akan dikaitkan dengan sejumlah kecil neuron di lapisan sebelumnya, bukannya terhubung ke semua neuron sebelumnya di lapisan. Selain itu, lapisan output untuk gambar dari set data CIFAR-10 akan memiliki dimensi 1 × 1 × 10, karena ketika mendekati akhir jaringan saraf kita akan mengurangi ukuran gambar menjadi vektor perkiraan kelas yang terletak di sepanjang kedalaman (dimensi 3).

Visualisasi:

Jaringan saraf standar	Jaringan Saraf Konvolusional

Sisi kiri: jaringan saraf 3 lapis standar.
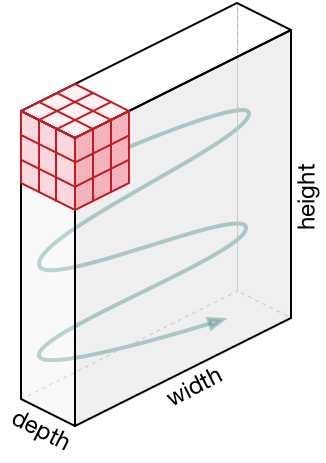
Di sisi kanan: jaringan saraf convolutional memiliki neuron dalam 3 dimensi (lebar, tinggi, kedalaman), seperti yang ditunjukkan pada salah satu lapisan. Setiap lapisan jaringan saraf konvolusional mengubah representasi 3D dari input menjadi representasi 3D dari output sebagai neuron aktivasi. Dalam contoh ini, lapisan input merah berisi gambar, sehingga ukurannya akan sama dengan ukuran gambar, dan kedalamannya adalah 3 (tiga saluran - merah, hijau, biru).

Jaringan saraf convolutional terdiri dari beberapa lapisan. Setiap lapisan adalah API sederhana: mengubah representasi 3D input menjadi representasi 3D output dari fungsi terdiferensiasi, yang mungkin atau mungkin tidak mengandung parameter.

Lapisan digunakan untuk membangun jaringan saraf convolutional

Seperti yang telah kami jelaskan di atas, jaringan saraf konvolusional sederhana adalah seperangkat lapisan, di mana setiap lapisan mengubah satu representasi menjadi yang lain menggunakan fungsi terdiferensiasi. Kami menggunakan tiga jenis utama lapisan untuk membangun jaringan saraf convolutional: lapisan konvolusional , lapisan subsampling , dan lapisan yang sepenuhnya terhubung (sama seperti yang kami gunakan dalam jaringan saraf normal). Kami mengatur lapisan ini secara berurutan untuk mendapatkan arsitektur SNA.

Contoh Arsitektur: Gambaran Umum. Di bawah ini kita akan membahas rinciannya, tetapi untuk sekarang, untuk dataset CIFAR-10, arsitektur jaringan saraf convolutional kami mungkin [INPUT -> CONV -> RELU -> POOL -> FC] . Sekarang lebih terinci:

• INPUT [32x32x3] akan berisi nilai asli piksel gambar, dalam kasus kami gambar tersebut berukuran lebar 32px, tinggi 32px, dan 3 saluran warna R, G, B.
• Lapisan CONV akan menghasilkan satu set neuron keluaran yang akan dikaitkan dengan area lokal dari gambar sumber input; setiap neuron tersebut akan menghitung produk skalar di antara bobotnya dan bagian kecil dari gambar aslinya yang terkait dengannya. Nilai output dapat berupa representasi 3D 323212 , jika, misalnya, kami memutuskan untuk menggunakan 12 filter.
• Lapisan RELU akan menerapkan fungsi aktivasi elemen max(0, x) . Konversi ini tidak akan mengubah dimensi data - [32x32x12] .
• Lapisan POOL akan melakukan operasi pengambilan sampel gambar dalam dua dimensi - tinggi dan lebar, yang sebagai hasilnya akan memberi kita representasi 3D baru [161612] .
• Lapisan FC (sepenuhnya terhubung lapisan) akan menghitung nilai berdasarkan kelas, dimensi yang dihasilkan akan [1x1x10] , di mana masing-masing dari 10 nilai akan sesuai dengan nilai kelas tertentu di antara 10 kategori gambar dari CIFAR-10. Seperti dalam jaringan saraf konvensional, setiap neuron dari lapisan ini akan dikaitkan dengan semua neuron dari lapisan sebelumnya (representasi 3D).

Ini adalah bagaimana jaringan saraf convolutional mengubah gambar asli, lapis demi lapis, dari nilai piksel awal ke estimasi kelas akhir. Perhatikan bahwa beberapa layer berisi opsi, dan beberapa tidak. Secara khusus, lapisan CONV/FC melakukan transformasi, yang tidak hanya fungsi yang tergantung pada data input, tetapi juga tergantung pada nilai internal dari bobot dan perpindahan dalam neuron itu sendiri. RELU/POOL , RELU/POOL lain, menggunakan fungsi non-parameter. Parameter dalam lapisan CONV/FC akan dilatih oleh gradient descent sehingga input menerima label output yang benar.

Untuk meringkas:

• Arsitektur jaringan saraf convolutional, dalam representasi yang paling sederhana, adalah seperangkat lapisan terurut yang mengubah representasi gambar menjadi representasi lain, misalnya, perkiraan keanggotaan kelas.
• Ada beberapa jenis lapisan (CONV - lapisan konvolusional, FC - sepenuhnya terhubung, fungsi aktivasi RELU, POOL - lapisan subsampel - yang paling populer).
• Setiap lapisan input menerima representasi 3D, mengubahnya menjadi representasi 3D output menggunakan fungsi terdiferensiasi.
• Setiap lapisan mungkin dan mungkin tidak memiliki parameter (CONV / FC - memiliki parameter, RELU / POOL - no).
• Setiap lapisan mungkin dan mungkin tidak memiliki parameter hyper (CONV / FC / POOL - have, RELU - no)

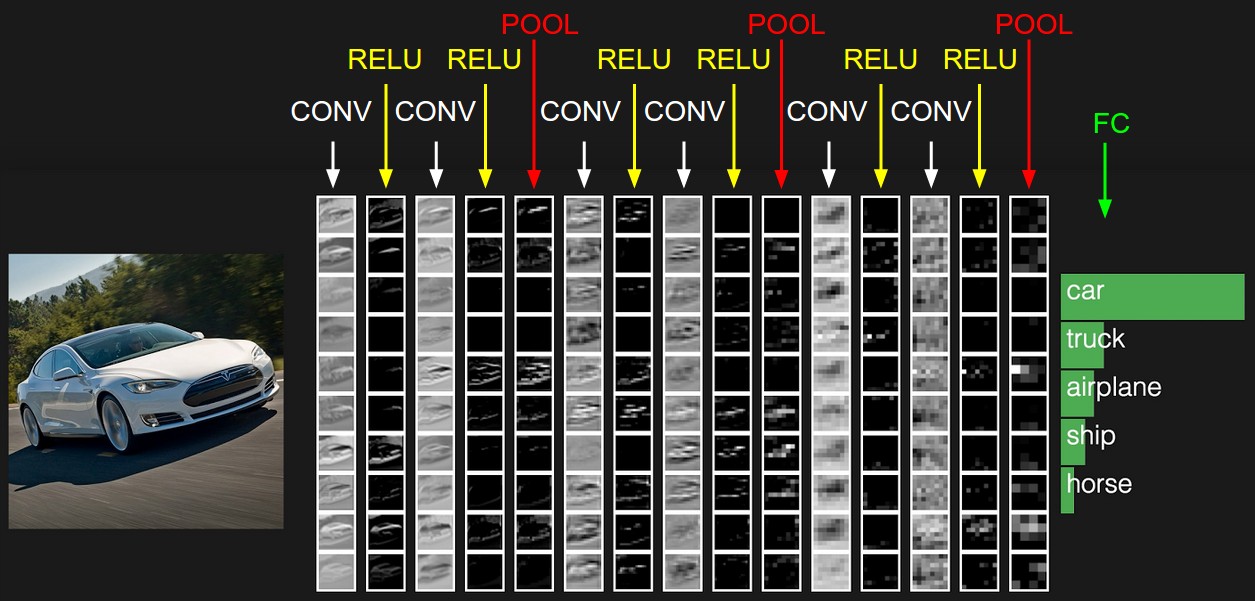
Representasi awal berisi nilai-nilai piksel dari gambar (di sebelah kiri) dan perkiraan untuk kelas-kelas yang menjadi objek objek di dalam gambar (di sebelah kanan). Setiap transformasi tampilan ditandai sebagai kolom.

Lapisan konvolusional

Lapisan convolutional adalah lapisan utama dalam pembangunan jaringan saraf convolutional.

Gambaran umum tanpa menyelam ke fitur otak. Mari kita pertama-tama mencoba mencari tahu apa yang lapisan CONV masih hitung tanpa membenamkan dan menyentuh subjek otak dan neuron. Parameter lapisan convolutional terdiri dari seperangkat filter terlatih. Setiap filter adalah kotak kecil sepanjang lebar dan tinggi, tetapi memanjang di seluruh kedalaman representasi input.

Misalnya, filter standar pada lapisan pertama dari jaringan saraf convolutional dapat memiliki dimensi 5x5x3 (lebar dan tinggi 5px, 3 - jumlah saluran warna). Selama pass langsung, kami memindahkan (tepatnya - kami runtuh) filter sepanjang lebar dan tinggi representasi input dan menghitung produk skalar antara nilai filter dan nilai yang sesuai dari representasi input di titik mana pun. Dalam proses memindahkan filter sepanjang lebar dan tinggi representasi input, kami membentuk peta aktivasi 2 dimensi yang berisi nilai-nilai menerapkan filter ini untuk masing-masing bidang representasi input. Secara intuitif, menjadi jelas bahwa jaringan akan mengajarkan filter untuk mengaktifkan ketika mereka melihat tanda visual tertentu, misalnya, garis lurus pada sudut tertentu atau representasi berbentuk roda di tingkat yang lebih tinggi. Sekarang kami telah menerapkan semua filter kami ke gambar asli, misalnya, ada 12. Sebagai hasil dari menerapkan 12 filter, kami menerima 12 kartu aktivasi dimensi 2. Untuk menghasilkan representasi output, kami menggabungkan kartu-kartu ini (berurutan dalam dimensi 3) dan mendapatkan representasi Dimensi [WxHx12].

Ikhtisar yang kami sambungkan ke otak dan neuron Jika Anda adalah penggemar otak dan neuron, Anda dapat membayangkan bahwa setiap neuron "melihat" bagian besar dari representasi input dan mentransfer informasi tentang bagian ini ke neuron tetangga. Di bawah ini kita akan membahas detail konektivitas neuron, lokasinya di ruang angkasa, dan mekanisme untuk berbagi parameter.

Konektivitas lokal. Ketika kita berurusan dengan input data dengan sejumlah besar dimensi, misalnya, seperti dalam kasus gambar, maka, seperti yang telah kita lihat, sama sekali tidak perlu untuk menghubungkan neuron dengan semua neuron pada lapisan sebelumnya. Sebagai gantinya, kami hanya akan menghubungkan neuron ke area lokal dari representasi input. Derajat konektivitas spasial adalah salah satu dari hiper-parameter dan disebut bidang reseptif (bidang reseptif neuron adalah ukuran filter / inti konvolusi yang sama). Tingkat konektivitas sepanjang dimensi ke-3 (kedalaman) selalu sama dengan kedalaman representasi asli. Sangat penting untuk fokus pada hal ini lagi, memperhatikan bagaimana kita mendefinisikan dimensi spasial (lebar dan tinggi) dan kedalaman: koneksi neuron adalah lebar dan tinggi lokal, tetapi selalu meluas ke seluruh kedalaman representasi input.

Contoh 1. Bayangkan bahwa representasi input memiliki ukuran 32x32x3 (RGB, CIFAR-10). Jika ukuran filter (bidang reseptif neuron) adalah 5 × 5, maka setiap neuron dalam lapisan konvolusional akan memiliki bobot di wilayah 5 × 5 × 3 dari representasi asli, yang pada akhirnya akan mengarah pada pembentukan 5 × 5 × 3 = 75 ikatan (bobot) + 1 parameter offset. Harap dicatat bahwa tingkat keterhubungan secara mendalam harus sama dengan 3, karena ini adalah dimensi dari representasi aslinya.

Contoh 2. Bayangkan bahwa representasi input memiliki ukuran 16x16x20. Dengan menggunakan sebagai contoh bidang reseptif dari neuron ukuran 3x3, setiap neuron lapisan konvolusional akan memiliki 3x3x320 = 180 koneksi (bobot) + 1 parameter perpindahan. Perhatikan bahwa konektivitas lokal memiliki lebar dan tinggi, tetapi kedalaman penuh (20).

# 1	# 2

Dari sisi kiri: representasi input ditampilkan dengan warna merah (misalnya, gambar berukuran 32x332 CIFAR-10) dan contoh representasi neuron di lapisan konvolusional pertama. Setiap neuron dalam lapisan konvolusional hanya dikaitkan dengan area lokal dari representasi input, tetapi sepenuhnya mendalam (dalam contoh, di sepanjang semua saluran warna). Harap dicatat bahwa ada banyak neuron dalam gambar (dalam contoh - 5) dan mereka berada di sepanjang dimensi ke-3 (kedalaman) - penjelasan mengenai pengaturan ini akan diberikan di bawah ini.
Di sisi kanan: neuron dari jaringan saraf masih tetap tidak berubah: mereka masih menghitung produk skalar antara bobot dan input data, menerapkan fungsi aktivasi, tetapi konektivitas mereka sekarang dibatasi oleh area lokal spasial.

Lokasi spasial. Kami telah menemukan konektivitas masing-masing neuron di lapisan konvolusional dengan representasi input, tetapi belum membahas berapa banyak neuron ini atau bagaimana mereka berada. Tiga parameter hiper mempengaruhi ukuran tampilan output: kedalaman , langkah, dan perataan .

1. Kedalaman representasi output adalah parameter hiper: itu sesuai dengan jumlah filter yang ingin kita terapkan, yang masing-masing mempelajari sesuatu yang lain dalam representasi asli. Misalnya, jika lapisan konvolusional pertama menerima gambar sebagai input, maka neuron yang berbeda di sepanjang dimensi ke-3 (kedalaman) dapat diaktifkan dengan adanya orientasi garis yang berbeda di area tertentu atau kelompok warna tertentu. Himpunan neuron yang "melihat" pada area yang sama dari representasi input, kita akan memanggil kolom yang dalam (atau "serat" - serat).
2. Kita perlu menentukan langkah (ukuran offset dalam piksel) dengan mana filter akan bergerak. Jika langkahnya 1, maka kami menggeser filter dengan 1 piksel dalam satu iterasi. Jika langkahnya 2 (atau, yang bahkan lebih jarang digunakan, 3 atau lebih), maka offset terjadi untuk setiap dua piksel dalam satu iterasi. Langkah yang lebih besar menghasilkan representasi output yang lebih kecil.
3. Seperti yang akan segera kita lihat, kadang-kadang perlu untuk melengkapi representasi input di sepanjang tepi dengan nol. Ukuran perataan (jumlah kolom / baris nol empuk) juga merupakan parameter hiper. Fitur bagus menggunakan alignment adalah kenyataan bahwa alignment akan memungkinkan kita untuk mengontrol dimensi representasi output (paling sering kita akan menjaga dimensi asli tampilan - menjaga lebar dan tinggi representasi input dengan lebar dan tinggi representasi output).

Kita dapat menghitung dimensi akhir dari representasi output dengan menghadirkannya sebagai fungsi dari ukuran representasi input ( W ), ukuran bidang reseptif dari neuron pada lapisan konvolusional ( F ), langkah ( S ) dan ukuran alignment ( P ) di perbatasan. Anda dapat melihat sendiri bahwa rumus yang tepat untuk menghitung jumlah neuron dalam representasi output adalah sebagai berikut (W - F + 2P) / S + 1 . Misalnya, untuk representasi input ukuran 7x7 dan ukuran filter 3x3, langkah 1 dan penyelarasan 0, kita mendapatkan representasi output berukuran 5x5. Pada langkah 2, kita akan mendapatkan representasi output 3x3. Mari kita lihat contoh lain, kali ini diilustrasikan secara grafis:

Ilustrasi pengaturan ruang. Dalam contoh ini, hanya satu dimensi spasial (sumbu x), satu neuron dengan bidang reseptif F = 3 , ukuran representasi input W = 5 dan perataan P = 1 . Di sisi kiri : bidang reseptif neuron bergerak dengan langkah S = 1 , yang sebagai hasilnya memberikan ukuran representasi output (5 - 3 + 2) / 1 + 1 = 5. Di sisi kanan : neuron menggunakan bidang reseptif ukuran S = 2 , yang pada hasilnya adalah ukuran representasi output (5 - 3 + 2) / 2 + 1 = 3. Perhatikan bahwa ukuran langkah S = 3 tidak dapat digunakan, karena dengan ukuran langkah ini bidang reseptif tidak akan menangkap bagian dari gambar. Jika kita menggunakan rumus kita, maka (5 - 3 + 2) = 4 bukan kelipatan 3. Bobot neuron dalam contoh ini adalah [1, 0, -1] (seperti yang ditunjukkan pada gambar paling kanan), dan offsetnya adalah nol. Bobot ini dibagi oleh semua neuron kuning.

Menggunakan perataan . Perhatikan contoh di sebelah kiri, yang berisi 5 elemen pada output dan 5 elemen pada output. Ini berhasil karena ukuran bidang reseptif (filter) adalah 3 dan kami menggunakan perataan P = 1 . Jika tidak ada keselarasan, maka ukuran representasi output akan sama dengan 3, karena justru banyak neuron yang cocok di sana. Secara umum, pengaturan ukuran pelurusan P = (F - 1) / 2 dengan langkah yang sama dengan S = 1 memungkinkan Anda untuk mendapatkan ukuran representasi keluaran yang sama dengan representasi input. Pendekatan serupa menggunakan penyelarasan sering diterapkan dalam praktek, dan kami akan membahas alasan di bawah ini ketika kita berbicara tentang arsitektur jaringan saraf convolutional.

Batas ukuran langkah . Harap dicatat bahwa parameter-hiper yang bertanggung jawab untuk pengaturan spasial juga terkait dengan keterbatasan. Misalnya, jika representasi input memiliki ukuran W = 10 , P = 0 dan ukuran bidang penerima F = 3 , maka menjadi tidak mungkin untuk menggunakan ukuran langkah sama dengan S = 2 , karena (W - F + 2P) / S + 1 = (10 - 3 + 0) / 2 + 1 = 4.5 , yang memberikan nilai integer dari jumlah neuron. Dengan demikian, konfigurasi parameter hiper dianggap tidak valid dan perpustakaan untuk bekerja dengan jaringan saraf convolutional akan mengeluarkan pengecualian, memaksa penyelarasan, atau bahkan memotong representasi input. Seperti yang akan kita lihat di bagian selanjutnya dari bab ini, definisi parameter-hiper dari lapisan konvolusional masih merupakan sakit kepala yang dapat dikurangi dengan menggunakan rekomendasi tertentu dan "aturan nada yang baik" ketika merancang arsitektur jaringan saraf convolutional.

Contoh kehidupan nyata . Arsitektur jaringan saraf convolutional Krizhevsky et al. , yang memenangkan kompetisi ImageNet pada 2012, menerima 227x227x3 gambar. Pada lapisan konvolusional pertama, ia menggunakan bidang reseptif ukuran F = 11 , langkah S = 4, dan ukuran penyelarasan P = 0 . Sejak (227 - 11) / 4 + 1 = 55, dan lapisan konvolusional adalah K = 96 , dimensi output dari presentasi adalah 55x55x96. Setiap neuron 55x55x96 dalam representasi ini dikaitkan dengan wilayah berukuran 11x11x3 dalam representasi input. Selain itu, semua 96 neuron di kolom dalam dikaitkan dengan wilayah 11x11x3 yang sama, tetapi dengan bobot yang berbeda. Dan sekarang sedikit humor - jika Anda memutuskan untuk berkenalan dengan dokumen asli (belajar), maka perhatikan bahwa dokumen tersebut menyatakan bahwa input menerima 224x224 gambar, yang tidak mungkin benar, karena (224 - 11) / 4 + 1 sama sekali tidak memberikan nilai integer. Situasi seperti ini sering membingungkan orang dalam cerita dengan jaringan saraf convolutional. Dugaan saya adalah bahwa Alex menggunakan ukuran pelurusan P = 3 , tetapi lupa menyebutkan ini dalam dokumen.

Opsi berbagi. Mekanisme untuk berbagi parameter di lapisan konvolusional digunakan untuk mengontrol jumlah parameter. Perhatikan contoh di atas, seperti yang Anda lihat ada 55x55x96 = 290.400 neuron pada lapisan konvolusional pertama dan masing-masing neuron memiliki 11x11x3 = 363 bobot + 1 nilai offset. Secara total, jika kita mengalikan dua nilai ini, kita mendapatkan 290400x364 = 105 705 600 parameter hanya pada lapisan pertama dari jaringan saraf convolutional. Jelas, ini sangat penting!

Ternyata adalah mungkin untuk mengurangi jumlah parameter secara signifikan dengan membuat satu asumsi: jika beberapa properti yang dihitung dalam posisi (x, y) penting bagi kami, maka properti ini yang dihitung dalam posisi (x2, y2) juga penting bagi kami. Dengan kata lain, menunjukkan kedalaman dua dimensi "lapisan" sebagai "lapisan dalam" (misalnya, tampilan [55x55x96] berisi 96 lapisan dalam, masing-masing berukuran 55x55), kami akan membangun neuron secara mendalam dengan bobot dan perpindahan yang sama. Dengan skema berbagi parameter ini, lapisan konvolusional pertama dalam contoh kita sekarang akan berisi 96 set bobot unik (masing-masing set untuk setiap lapisan kedalaman), secara total akan ada 96x11x11x3 = 34.848 bobot unik atau 34.944 parameter (+96 offset). Selain itu, semua neuron 55x55 di setiap lapisan dalam sekarang akan menggunakan parameter yang sama. Dalam praktiknya, selama propagasi balik, setiap neuron dalam representasi ini akan menghitung gradien untuk bobotnya sendiri, tetapi gradien ini akan dijumlahkan pada setiap lapisan kedalaman dan memperbarui hanya satu set bobot di setiap level.

Perhatikan bahwa jika semua neuron dalam lapisan dalam yang sama menggunakan bobot yang sama, maka untuk propagasi langsung melalui lapisan konvolusional, konvolusi antara nilai-nilai bobot neuron dan data input akan dihitung. Itulah sebabnya lazim untuk memanggil satu set bobot - filter (inti) .

Contoh filter yang diperoleh dengan melatih model Krizhevsky et al. Masing-masing dari 96 filter yang ditampilkan di sini berukuran 11x11x3 dan masing-masing dibagikan oleh semua neuron 55x55 dari satu lapisan dalam. Harap perhatikan bahwa asumsi berbagi bobot yang sama masuk akal: jika deteksi garis horizontal penting di satu bagian gambar, maka secara intuitif jelas bahwa deteksi semacam itu penting di bagian lain gambar ini. Oleh karena itu, tidak masuk akal untuk melatih ulang setiap waktu untuk menemukan garis horizontal di setiap 55x55 tempat gambar yang berbeda di lapisan convolutional.

Harus diingat bahwa asumsi parameter berbagi mungkin tidak selalu masuk akal. Misalnya, jika gambar dengan struktur terpusat diumpankan ke input dari jaringan saraf convolutional, di mana kami ingin dapat mempelajari satu properti di satu bagian gambar dan properti lain di bagian lain gambar. Contoh praktisnya adalah gambar wajah terpusat. Dapat diasumsikan bahwa tanda mata atau rambut yang berbeda dapat diidentifikasi pada area gambar yang berbeda, oleh karena itu, dalam hal ini, relaksasi bobot digunakan dan lapisan tersebut disebut terhubung secara lokal .

Contoh-contoh kotor . Diskusi sebelumnya harus ditransfer ke bidang spesifik dan pada contoh dengan kode. Bayangkan representasi input adalah array numpy X Lalu:

• Kolom dalam ( utas ) pada posisi (x,y) akan direpresentasikan sebagai berikut X[x,y,:] .
• Lapisan dalam , atau seperti yang kita sebut lapisan sebelumnya - peta aktivasi pada kedalaman d akan direpresentasikan sebagai berikut X[:,:,d] .

Contoh lapisan konvolusional . , X X.shape: (11,11,4) . , P=1 , () F=5 S=1 . 44, — (11-5)/2+1=4. ( V ), ( ):

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

, numpy , * . , W0 b0 . W0 W0.shape: (5,5,4) , 5, 4. . , , 2 ( ). :

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
• V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (, y )
• V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (, )

— W1 b1 . , V . , , , ReLU , . .

. :

• W1 x H1 x D1
• 4 -:
  
  • K ,
  • F ,
  • S ,
  • P .
• W2 x H2 x D2 ,
  
  • W2 = (W1 — F + 2P)/S + 1
  • H2 = (H1 — F + 2P)/S + 1
  • D2 = K
• F x F x D1 , (F x F x D1) x K K .
• , d - ( W2 x H2 ) d - S d -.

- F = 3, S = 1, P = 1 . . " ".

. . 3D- ( — , — , — ), — . W1 = 5, H1 = 5, D1 = 3 , K = 2, F = 3, S = 2, P = 1 . , 33, 2. (5 — 3 + 2)/2 + 1 = 3. , , P = 1 . , () , .

( , html+css , )

. (). :

1. im2col . , 227x227x3 11113 4, 11113 = 363 . , 4 , (227 — 11) / 4 + 1 = 55 , X_col 3633025, 3025. , , , (), .
2. . , 96 11113, W_row 96363.
3. — np.dot(W_row, X_col) , . 963025.
4. 555596.

, , — , . , , — (, BLAS API). , im2col , .

. ( ) ( , ) ( - ). , .

11 . 11, Network in Network . , 11, , . , 2- , 11 ( ). , , 3- , . , 32323, 11, , , 3 (R, G, B — , ).

. - . . , . w 3 x : w[0] x[0] + w[1] x[1] + w[2] x[2] . 0. 1 : w[0] x[0] + w[1] x[2] + w[2] x[4] . "" 1 . , . , 2 33, , 55 ( 55 ). .

— . , , . , MAX. 22 2, 2 , 75% . MAX 22. . , :

• W1 x H1 x D1
• 2 -:
  
  • F ,
  • S ,
• W2 x H2 x D2 , :
  
  • W2 = (W1 — F)/S + 1
  • H2 = (H1 — F)/S + 1
  • D2 = D1
• ,
• (zero-padding ).

, : F=3, S=2 ( ), — F=2, S=2 . - .

. , , , L2-. , , .

# 1	# 2

. : 22422464 22 2, 11211264. , . : — (max-pooling), 2. 4 ( 22)

. , max(a,b) — . , ( ), .

. , . , : , . . , (VAEs) (GANs). , - , .

, , . , , . .

, . .

, , ( ). - , . , :

• , . , , , , , .
• , . , K=4096 ( ), 7712 - F=7, P=0, S=1, K=4096 . , 114096, .

. , . , 2242243 77512 ( AlexNet, , 5 , 7 — 224/2/2/2/2/2 = 7). AlexNet 4096 , , 1000 , . :

• , "" 77512, F=7 , 114096.
• F=1 , 114096.
• F=1 , 111000.

, , ( ) W . , "" () .

, 224224 , 77512 — 32 , 384384 1212512, 384/32 = 12. , , , 661000, (12 — 7)/1 + 1 = 6. , 111000 66 384384 .

( ) 384384, 224244 32 , , .

, , 36 , 36 . , , . .

, , 32 ? ( ). , 16 , 2 : 16 .

, , 3 : , ( , ) . ReLU , - . .

CONV-RELU-, POOL- , . - . , , . , :

 INPUT -> [[CONV -> RELU]*N -> POOL?] * M -> [FC -> RELU]*K -> FC 

* , POOL? . , N >= 0 ( N <= 3 ), M >= 0 , K >= 0 ( K < 3 ). , , :

• INPUT -> FC , . N = M = K = 0 .
• INPUT -> CONV -> RELU -> FC
• INPUT -> [CONV -> RELU -> POOL] * 2 -> FC -> RELU -> FC , .
• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL] * 3 -> [FC -> RELU] * 2 -> FC . 2 . , , .

. 3 33 ( RELU , ). "" 33 . "" 33 , — 55. "" 33 , — 77. , 33 77. "" 77 ( ) , . -, , 3 , . -, C , , 77 (C(77)) = 49xxC , 33 3((33)) = 27 . , , . — , .

. , , Google, Microsoft. .

: , ImageNet. , , 90% . — " ": , , , ImageNet — , . .

-, . , :

( ) 2 . 32 (, CIFAR-10), 64, 96 (, STL-10), 224 (, ImageNet), 384 512.

(, 33 , 55), S=1 , , , . , F=3 P=1 . F=5, P=2 . F , P=(F-1)/2 . - ( 77), .

. 22 ( F=2 ) 2 ( S=2 ). , 75% (- , ). , , 33 ( ) 2 ( ). 33 , . .

. , , . , 1 , , .

1 ? . , 1 ( ), .

? , . , , , .

. ( ), , . , 64 33 1 2242243, 22422464. , , 10 , 72 ( , ). GPU, . , 77 2. , AlexNet, 1111 4.

. :

• LeNet . Yann LeCun 1990. LeNet , ZIP-, .
• AlexNet . , , Alex Krizhevsky, Ilya Sutskever Geoff Hinton. AlexNet ImageNet ILSVRC 2012 ( : 16% 26%). LeNet, , ( ).
• ZFNet . ILSVRC 2013 Matthew Zeiler Rob Fergus. ZFNet. AlexNet, -, .
• GoogLeNet . ILSVRC 2014 Szegedy et al. Google. Inception-, (4 60 AlexNet). , , . , — Inveption-v4.
• VGGNet . 2014 ILSVRC Karen Simonyan Andrew Zisserman, VGGNet. , . 16 + (33 22 ). . VGGNet — (140). , , , .
• ResNet . Residual- Kaiming He et al. ILSVRC 2015. . . ( 2016).

VGGNet . VGGNet . VGGNet , 33, 1 1, 22 2. ( ) :

 INPUT: [224x224x3] memory: 224*224*3=150K weights: 0 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*3)*64 = 1,728 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*64)*64 = 36,864 POOL2: [112x112x64] memory: 112*112*64=800K weights: 0 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*64)*128 = 73,728 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*128)*128 = 147,456 POOL2: [56x56x128] memory: 56*56*128=400K weights: 0 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*128)*256 = 294,912 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 POOL2: [28x28x256] memory: 28*28*256=200K weights: 0 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*256)*512 = 1,179,648 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 POOL2: [14x14x512] memory: 14*14*512=100K weights: 0 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 POOL2: [7x7x512] memory: 7*7*512=25K weights: 0 FC: [1x1x4096] memory: 4096 weights: 7*7*512*4096 = 102,760,448 FC: [1x1x4096] memory: 4096 weights: 4096*4096 = 16,777,216 FC: [1x1x1000] memory: 1000 weights: 4096*1000 = 4,096,000 TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd) TOTAL params: 138M parameters 

, , ( ) , . 100 140 .

. GPU 3/4/6 , GPU — 12 . , :

• : , ( ). , . , .
• : , , . , , 3 .
• , , ..

(, ), . , 4 ( 4 , — 8), 1024 , , . " ", , .

… call-to-action — , share :)
YouTube
Telegram
VKontakte