☕️ 👨🏾‍✈️ 🔻 Dunia hipersphere tiga dimensi. Penelusuran sinar geodesik di alam semesta tertutup dengan geometri bola 👩🏿‍🚒 🎮 👲🏼

Apakah Anda ingin melihat dunia melalui mata makhluk hidup di alam semesta yang tertutup rapat dengan geometri bola? Lihat dunia tanpa malam? Dunia di mana kutub lain planet ini terlihat di langit? Dunia di mana tidak ada perbedaan antara gerhana matahari dan bulan? Selamat datang di kucing!

Pendahuluan Dunia tertutup dua dimensi

Untuk lebih memahami apa yang akan terjadi selanjutnya, bayangkan Anda adalah makhluk dua dimensi dan hidup di dunia dua dimensi yang mewakili bola. Bagaimana Anda memandang dunia Anda? Mari kita mulai dengan menentukan posisi tubuh. Anda dapat mendeklarasikan titik di mana Anda adalah "pusat alam semesta", pilih dua vektor satuan yang saling tegak lurus dan gunakan sistem koordinat Kartesius yang dihasilkan di sekitar "pusat alam semesta".

Namun, ketika Anda menjauh dari "pusat alam semesta" hal-hal aneh akan mulai terjadi. Apa yang Anda anggap sebagai garis tegak lurus, dengan jarak tertentu dari "pusat alam semesta" berubah menjadi apa yang Anda anggap sebagai garis paralel ...

... Dan garis paralel berpotongan.

Alasannya sederhana - apa yang Anda anggap sebagai garis lurus sebenarnya adalah lingkaran besar - garis geodesik bola. Karena itu, sistem koordinat Kartesius tidak cocok untuk menentukan posisi tubuh di dunia Anda - ketika Anda menjauh dari "pusat alam semesta", sistem itu kehilangan maknanya.

Anda harus memilih yang lain, lebih cocok untuk digunakan di dunia Anda, sistem koordinat - kutub . Sistem koordinat ini alami dan konsisten. Memang - sudut antara sumbu kutub dan arah ke tubuh tetap konstan terlepas dari jarak ke tubuh.

Mampu menentukan posisi tubuh, kami dapat menjelajahi dunia Anda secara mental dan menggambarkan beberapa efek yang muncul saat Anda menjauh dari "pusat alam semesta" dan karena kenyataan bahwa dunia Anda adalah bola.

Perspektif sebaliknya . Biasanya, ketika sebuah benda menjauh dari "pusat alam semesta," ukuran sudutnya berkurang. Namun, pada jarak lebih dari seperempat panjang garis geodesik dari "pusat alam semesta" dengan pengangkatan tubuh, ukuran sudutnya akan meningkat. Efek ini disebabkan oleh fakta bahwa jarak antara garis geodesik dari bola ke ekuator meningkat, dan setelah ekuator berkurang. Sebuah benda jarak jauh dengan jarak yang sama dari khatulistiwa akan memiliki ukuran sudut yang sama, terlepas dari sisi mana ia berada dari khatulistiwa. Dan ukuran sudut ini akan lebih besar dari ukuran sudut tubuh di garis katulistiwa.

Meregangkan tubuh di langit. Di sini istilah seluruh langit digunakan dalam arti - seluruh bidang pandangan makhluk dua dimensi (atas dan bawah atau depan dan belakang). Jika tubuh berada di dekat titik yang berlawanan dengan "pusat alam semesta", maka ke mana pun Anda melihat, Anda akan bertemu dengan tubuh ini. Tubuh tidak akan memiliki titik yang tidak dapat dilihat - setiap titik memiliki tempat di langit. Ini adalah kasus utama dari efek perspektif terbalik.

Transformasi simetris tel. Jika tubuh berada pada jarak lebih dari setengah panjang garis geodetik dari "pusat alam semesta", maka Anda akan melihat tubuh ini diubah secara simetris - sisi kiri dan kanan tubuh akan mengubah tempat. Biasanya sinar kiri dan kanan yang dipancarkan dari "pusat alam semesta" jatuh di sisi kiri dan kanan tubuh. Namun, pada jarak setengah panjang garis geodesik dari "pusat alam semesta", sinar berpotongan dan setelah menyeberang jatuh ke sisi yang berlawanan dari tubuh.

Perspektif maju dan mundur kedua. Efek ini juga diamati jika tubuh berada pada jarak yang lebih besar dari setengah panjang garis geodesik dari "pusat alam semesta." Pada jarak dari setengah hingga tiga perempat dari panjang garis geodesik dari "pusat alam semesta," dengan penghapusan tubuh, ukuran sudutnya akan berkurang lagi (perspektif langsung). Pada jarak dari tiga perempat ke seluruh panjang garis geodesik dari "pusat alam semesta", ketika tubuh bergerak menjauh, ukuran sudutnya akan meningkat lagi (perspektif terbalik). Efek ini, serta efek perspektif terbalik, dikaitkan dengan perubahan jarak antara garis geodesik bola - dalam perjalanan kembali ke "pusat alam semesta", jarak antara garis geodetik bola ke khatulistiwa meningkat, dan menurun setelah khatulistiwa.

Ganda. Setiap tubuh di dunia Anda akan memiliki dobel - jika Anda melihat tubuh di depan Anda, kemudian berbalik Anda dapat melihat sisi yang berlawanan (dobel). Sinar yang dipancarkan di sepanjang jalan panjang mengelilingi dunia Anda dan memasuki bagian belakang tubuh. Perlu dicatat bahwa permukaan ganda akan menjadi bagian dari permukaan yang tidak Anda lihat di depan Anda, dan itu akan diubah secara simetris. Di sini, istilah permukaan digunakan dalam arti - batas benda dua dimensi yang dirasakan oleh makhluk dua dimensi - seperti yang diterapkan pada sebuah lingkaran, itu sebenarnya adalah busur lingkaran yang dirasakan oleh makhluk dua dimensi sebagai sebuah segmen, namun, untuk kejelasan, kita akan menyoroti tidak hanya busur, tetapi juga bagian dari lingkaran yang berada di belakangnya.

Bagian tubuh melalui titik yang berlawanan dengan "pusat alam semesta." Karena efek meregangkan tubuh ke seluruh langit sangat tidak biasa, kami akan mempertimbangkannya secara lebih rinci. Dalam gambar: lingkungan titik berlawanan dengan "pusat alam semesta."

Terlihat bahwa:

pertama, permukaan tubuh di depan Anda bertambah (dicat biru), dan yang di belakang Anda berkurang (dicat biru); pada saat yang sama, kedua permukaan memiliki dimensi sudut yang sama - yaitu, permukaan tubuh yang terletak di depan Anda berkontraksi (sebagian besar permukaan terletak pada setiap derajat), dan permukaan yang terletak di belakang Anda ditarik (semua bagian permukaan yang lebih kecil terletak pada setiap derajat)
ketika tubuh menyentuh titik berlawanan dengan "pusat alam semesta" ukuran sudut dari kedua permukaan adalah 180 derajat - satu setengah dari langit (di depan Anda) menempati seluruh permukaan tubuh, dan bagian kedua dari langit (di belakang Anda) ditempati oleh titik yang terletak di belakang tubuh
sementara pusat tubuh disejajarkan dengan titik yang berlawanan dengan "pusat alam semesta", proses menarik mundur dan peregangan
ketika tubuh terletak pada titik yang berlawanan dengan "pusat alam semesta", permukaannya tidak terdistorsi membentang di seluruh langit
tubuh meluncur dari titik yang berlawanan dengan "pusat alam semesta" terlihat serupa

Cakrawala ganda. Bayangkan Anda hidup di planet dua dimensi. Melihat ke bawah, Anda melihat permukaan sisi planet Anda, dan melihat ke atas, Anda melihat ... permukaan bagian belakang planet ini. Selain itu, itu akan sangat ketat - Anda dapat melihat permukaan bagian belakang planet ini dan bagian permukaan sisi planet Anda yang berada di belakang punggung Anda di belakang cakrawala - Anda dapat melihat semua ini di atas kepala Anda. Langit akan disajikan dalam bentuk strip sempit seperti benang, diapit dari atas dan bawah oleh cakrawala sisi Anda dan sebaliknya dari planet ini. Ini adalah kombinasi dari efek peregangan tubuh di seluruh langit dan efek ganda. Secara umum, di dunia Anda, jika tidak ada yang mengganggu pandangan Anda, maka tepat di depan Anda, Anda dapat melihat tengkuk Anda ... tengkuk yang sangat sehat, dalam semua detailnya ... diperluas ke seluruh langit)

Dunia tanpa malam. Bayangkan bahwa planet dua dimensi tempat Anda hidup berputar di sekitar bintang dua dimensi. Cahaya yang dipancarkan oleh bintang di jalur pendek jatuh di sisi siang hari planet ini. Pada saat yang sama, cahaya yang dipancarkan oleh bintang di sepanjang jalan panjang mengelilingi dunia Anda dan jatuh di sisi malam planet ini. Malam tidak ada lagi. Yang tersisa hanyalah matahari terbenam dan matahari terbit yang akan terjadi secara bersamaan - ketika sisi bintang yang menghadap Anda mulai melampaui cakrawala, sisi belakang bintang akan mulai naik di belakang Anda dari balik cakrawala. Tentu saja, Anda dapat menyorot matahari terbenam dan fajar yang sebenarnya di sepanjang jalan setapak yang dilewati cahaya, tetapi akan hampir mustahil untuk membedakannya dari ganda.

Ada juga kasus ekstrem. Jika planet ini bernasib sial dan berada di titik bintang yang berseberangan, maka bintang itu akan terentang ke seluruh langit, tetapi akan menjadi masalah untuk mengaguminya, karena semua cahaya yang dipancarkan oleh bintang itu akan jatuh di planet tersebut (jika tidak ada penyerapan cahaya dan hamburan oleh media antarplanet).

Gerhana matahari dan bulan. Bayangkan bahwa satelit alami dua dimensi berputar di sekitar planet dua dimensi tempat Anda tinggal. Ketika satelit menjadi antara planet dan bintang, bayangannya jatuh di planet ini. Di sisi lain, pada saat yang sama, planet ini menjadi antara cahaya yang dipancarkan bintang sepanjang jalur panjang dan satelit, yaitu bayangan planet jatuh pada satelit. Terjadi gerhana matahari dan bulan secara simultan. Tentu saja, adalah mungkin untuk membedakan gerhana matahari dan bulan yang sebenarnya di sepanjang lintasan yang dilewati cahaya, tetapi secara praktis tidak mungkin untuk membedakan mereka dari kembar. Jatuh ke bayangan yang jatuh di planet ini dan satelitnya selama gerhana adalah satu-satunya cara untuk berada dalam kegelapan di dunia Anda)

Dunia tertutup tiga dimensi

Di atas, kami memeriksa dunia yang indah dari makhluk dua dimensi. Bagaimana dengan kita makhluk tiga dimensi? Apa geometri alam semesta ? Sayangnya, sains belum dapat menjawab pertanyaan ini. Terutama sifat-sifat dan ukuran Semesta yang mengganggu. Mari kita coba bantu sains. Kami memilih sebagai kandidat, alam semesta tertutup yang paling menarik dengan geometri bola dan memeriksanya secara visual. Akankah ada efek yang ditemukan oleh kami untuk analog dua dimensi? Mungkin kita akan belajar sesuatu yang baru? Sesuatu yang tidak Anda harapkan tahu? Atau bahkan melihat apa yang kita lihat setiap hari, tetapi tidak memperhatikannya? Seperti apakah jagat raya itu?

Model

Kita akan menjelajahi dunia, yang merupakan hypersphere tiga dimensi (3-sphere) - yaitu, sebuah bola yang terletak di ruang empat dimensi. Kami memilih satu jenis objek untuk visualisasi - bola (bola 2 milik bola 3).

Konsep dan hubungan dasar

Koordinat kartesius dalam ruang empat dimensi - kita akan menyatakannya sebagai

$(x_0, x_1, x_2, x_3)$ - ini sebenarnya

$(x, y, z, w)$ .

Koordinat hipersferis dalam ruang empat dimensi (kita hanya menggunakan sudut, karena jari-jari dunia kita akan konstan) - kita akan menyatakannya sebagai

$(a_0, a_1, a_2)$ - ini sebenarnya

$(\ phi, \ theta, \ psi)$ .

3 bola yang berpusat pada titik asal - satu set titik yang radius vektornya memiliki panjang sama dengan jari-jari bola 3

$R$ Apakah dunia kita

$\ quad \ quad x_0 ^ 2 + x_1 ^ 2 + x_2 ^ 2 + x_3 ^ 2 = R ^ 2$

2-bola milik 3-bola - seperangkat titik yang radius vektornya memiliki panjang sama dengan jari-jari 3-bola

$R$ dan bentuk dengan vektor jari-jari pusat 2-bola

$c$ sudut sama dengan jari-jari sudut bola-2

$r_a$ Adalah objek visualisasi kami

$\ quad \ quad x_0 c_0 + x_1 c_1 + x_2 c_2 + x_3 c_3 = R ^ 2 \ cos r_a$

dimana

$\ quad \ quad r_a = r / R$

$\ quad \ quad r$ - Jari-jari geodesik dari 2-bola

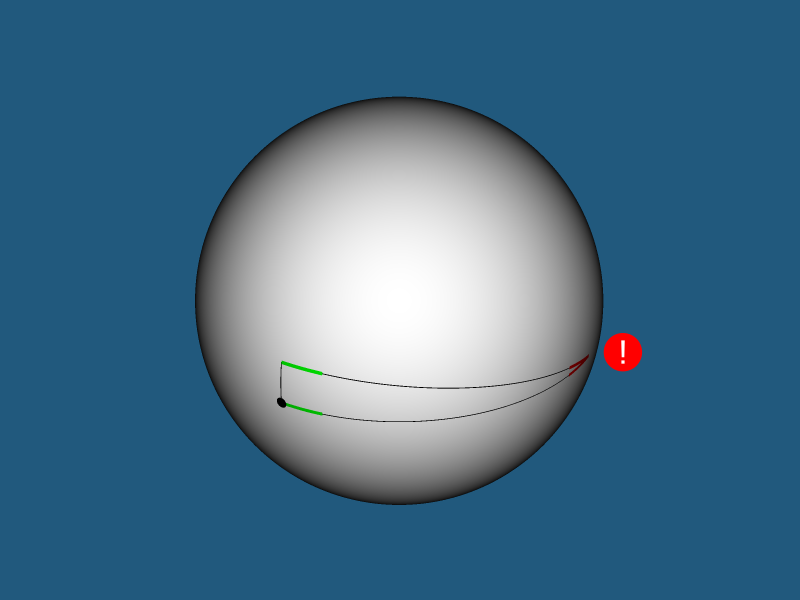
Jari - jari geodesik, sudut dan bersyarat - untuk lebih memahami apa itu, pertimbangkan analog dua dimensi dari bola-2 yang dimiliki bola-3 - sebuah lingkaran yang dimiliki bola.

Busur merah pada gambar adalah jari-jari geodesik dari lingkaran

$r$ . Sudut merah di sisi kanan gambar adalah jari-jari sudut lingkaran

$r_a = r / R$ . Ketinggian segitiga di sisi kanan gambar adalah jari-jari bersyarat dari lingkaran

$r_n = R \ sin r_a$ .

Transisi dari koordinat hipersferis

$(a_0, a_1, a_2)$ ke kartesian

$(x_0, x_1, x_2, x_3)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

dimana

$\ quad \ quad a_0$ bervariasi dari

$0$ sebelumnya

$2 \ pi$

$\ quad \ quad a_1$ bervariasi dari

$0$ sebelumnya

$\ pi$

$\ quad \ quad a_2$ bervariasi dari

$0$ sebelumnya

$\ pi$

Perpotongan garis geodesik dari bola 3 dengan bola 2 milik bola 3.
Rasio ini akan digunakan untuk penelusuran sinar. Biarkan ada garis geodesik memanjang dari kutub 3-bola

$(0, 0, 0, R)$ dalam arah yang ditentukan oleh sudut

$a_0$ dan

$a_1$ - sudut ini bertepatan dengan sudut yang menentukan arah dalam ruang tiga dimensi di sekitar kutub 3-bola

$(0, 0, 0, R)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

penyederhanaan yang kita miliki (1)

$\ quad \ quad x_0 = r_0 \ sin a_2$

$\ quad \ quad x_1 = r_1 \ sin a_2$

$\ quad \ quad x_2 = r_2 \ sin a_2$

$\ quad \ quad x_3 = r_3 \ cos a_2$

dimana

$\ quad \ quad r_0 = R \ sin a_1 \ cos a_0$

$\ quad \ quad r_1 = R \ sin a_1 \ sin a_0$

$\ quad \ quad r_2 = R \ cos a_1$

$\ quad \ quad r_3 = R$

mengganti (1) dalam persamaan 2-bola dan menyederhanakan yang kita miliki (2)

$\ quad \ quad A \ sin a_2 + B \ cos a_2 = C$

dimana

$\ quad \ quad A = r_0 c_0 + r_1 c_1 + r_2 c_2$

$\ quad \ quad B = r_3 c_3$

$\ quad \ quad C = R ^ 2 \ cos r_a$

mengganti (1) dalam persamaan 3-bola dan menyederhanakan yang kita miliki (3)

$\ quad \ quad D \ sin ^ 2 a_2 + E \ cos ^ 2 a_2 = F$

dimana

$\ quad \ quad D = r_0 ^ 2 + r_1 ^ 2 + r_2 ^ 2$

$\ quad \ quad E = r_3 ^ 2$

$\ quad \ quad F = R ^ 2$

mengungkapkan dari (2)

$\ cos a_2$ kami punya

$\ quad \ quad \ cos a_2 = (C - A \ sin a_2) / B$

mengganti (3)

$\ cos a_2$ kami punya

$\ quad \ quad D \ sin ^ 2 a_2 + E / B ^ 2 (C - A \ sin a_2) ^ 2 = F$

menyederhanakan yang kita miliki

$\ quad \ quad a \ sin ^ 2 a_2 + b \ sin a_2 + c = 0$

dimana

$\ quad \ quad m = E / B ^ 2$

$\ quad \ quad a = m A ^ 2 + D$

$\ quad \ quad b = -2 m A C$

$\ quad \ quad c = m C ^ 2 - F$

Suatu titik pada kelanjutan dari garis geodesik dari bola 3 yang melewati dua titik.
Relasi ini akan digunakan untuk menemukan koordinat tekstur dan normal eksternal pada titik arbitrer dari 2-bola milik 3-bola. Biarkan

$\ quad \ quad O$ - Pusat 3-bola

$\ quad \ quad A$ - pusat 2-bola

$\ quad \ quad B$ Merupakan titik arbitrer dari 2-bola

$\ quad \ quad C$ - titik yang diinginkan terletak pada kelanjutan dari garis geodetik

$AB$ pada jarak sudut kecil

$\ delta$ dari titik

$B$

$\ quad \ quad D$ - titik persimpangan garis

$AB$ dan

$OC$

$\ quad \ quad E$ - titik persimpangan garis yang melewati titik

$D$ tegak lurus ke lurus

$AB$ dan garis melewati titik

$O$ sejajar dengan lurus

$AB$

$\ quad \ quad r_a$ - radius sudut 2-bola

$\ quad \ quad a = (\ pi - r_a) / 2$

$\ quad \ quad b = a - \ delta$
Jika

$r_a> \ pi$ maka harus diletakkan

$r_a = 2 \ pi - r_a$ , dan

$\ delta = - \ delta$
Akan menemukan

$\ vec {OD}$

$\ quad \ quad \ vec {OD} = \ vec {OA} + \ vec {AB} / | \ vec {AB} | \ cdot | \ vec {AD} |$

dimana

$\ quad \ quad | \ vec {AD} | = | \ vec {AB} | / 2 + | \ vec {OE} |$

$\ quad \ quad | \ vec {OE} | = | \ vec {DE} | / \ tan b$

$\ quad \ quad | \ vec {DE} | = R \ sin a$

akan menemukan

$\ vec {OC}$

$\ quad \ quad \ vec {OC} = \ vec {OD} / | \ vec {OD} | \ cdot R$

Pencahayaan

Kami akan menggunakan dua model pencahayaan.

Model pencahayaan sederhana. Dalam model ini, kecerahan titik permukaan tergantung pada kosinus sudut antara normal eksternal ke permukaan dan arah ke pengamat. Kami akan menggunakannya saat membuat gambar untuk materi penjelasan. Bahkan, ini adalah model dengan sumber cahaya titik yang terletak di mana pengamat berada, di mana kecerahan titik permukaan tidak tergantung pada jarak ke sumber cahaya.

Model pencahayaan realistis. Model ini akan memiliki sumber cahaya khusus. Kami akan menggunakannya ketika membangun gambar yang realistis. Model ini dapat memperhitungkan pengaruh area muka gelombang terhadap kecerahan titik permukaan (pada kenyataannya, pengaruh jarak ke sumber cahaya). Dalam alam semesta tertutup dengan geometri bola, area muka gelombang berbanding lurus dengan kuadrat dari jari-jari bersyarat bola dengan jari-jari geodesi yang sama dengan jarak dari titik permukaan ke sumber cahaya. Dengan jarak dari sumber cahaya, area muka gelombang ke khatulistiwa meningkat (sinar menyimpang), dan setelah khatulistiwa berkurang (sinar cahaya menyatu, fokus). Setelah melewati titik yang berlawanan dengan "pusat alam semesta", proses sebaliknya terjadi: sinar cahaya pertama menyimpang, dan kemudian bertemu kembali. Selain itu, model ini dapat memperhitungkan kekhasan persepsi akun ( hukum Weber - Fechner ).

Untuk membangun gambar, kita akan menggunakan tracing ray terbalik . Agar model menjadi interaktif (kita akan memeriksa dunia kita dan bergerak di dalamnya), gambar harus dibangun secara real time. Oleh karena itu, kami akan melakukan perhitungan dalam fragmen shader (kami menggunakan WebGL). Kami mengimplementasikan antarmuka dalam JavaScript.

Tekstur

Tekstur earth.jpg dari sini

Tekstur moon.jpg dari sini

Tekstur sun.png dari sini

Kenalan pertama

Kita akan menciptakan dunia tertutup tiga dimensi dengan panjang garis geodesik 100 - sehingga akan lebih mudah bagi kita untuk menavigasi - khatulistiwa dunia kita akan terletak pada jarak 25 (seperempat panjang garis geodesik), dan kutub yang berlawanan dari dunia kita - pada jarak 50 (setengah panjang garis geodesik). Kami menempatkan sebuah planet di dunia kami dan mengecat bagian permukaannya dengan warna tergantung pada oktan mana mereka jatuh:

Oktan	Tanda X	Tanda Y	Tanda Z	Warna
Saya	+	+	+	Merah (red)
II	-	+	+	Hijau ( G reen)
III	-	-	+	Biru ( B lue)
IV	+	-	+	Oranye
V	+	+	-	Biru ( C yan)
VI	-	+	-	Ungu ( M agenta)
VII	-	-	-	Kuning ( Y ellow)
VIII	+	-	-	Putih

Sebagai tekstur utama, kita akan menggunakan tekstur papan catur 3x6, yaitu setiap paralel dan meridian akan melewati 12 sel. Sebagai tekstur alternatif, kita akan menggunakan tekstur globe. Di bawah ini adalah gambar-gambar flyby pembiasaan dari planet kita.

Cuplikan dari Kutub Utara. Sumbu X diarahkan ke kanan, sumbu Y diarahkan ke atas, sumbu Z diarahkan pada kami. Saat menerapkan tekstur alternatif, Anda dapat melihat:

di sebelah kanan adalah Samudra Pasifik
Di atas - Amerika Utara
kiri - Samudra Atlantik
bawah - Eurasia

Foto penerbangan dari Kutub Utara ke khatulistiwa dan dari khatulistiwa ke Kutub Selatan.

Snapshot dari Kutub Selatan. Sumbu X diarahkan ke kanan, sumbu Y diarahkan ke bawah, sumbu Z diarahkan menjauh dari kita. Saat menerapkan tekstur alternatif, Anda dapat melihat:

Kanan - Samudra Pasifik, Selandia Baru, Australia
dari atas - Samudra Hindia
kiri - Samudera Atlantik, Afrika
bawah - Amerika Selatan

Studi visual

Kami akan melakukan studi visual dari dunia kami untuk menemukan analog dari efek yang kami temukan di dunia tertutup dua dimensi.

Ganda. Seperti pada analog dua dimensi, setiap tubuh di dunia kita akan memiliki dua kali lipat - jika kita melihat Kutub Utara di depan kita, maka berbaliklah kita dapat melihat ... Kutub Selatan. Kontraksi permukaan ganda terlihat karena fakta bahwa kita cukup dekat dengan planet ini.

Eksperimen di mana pengamat bergerak menjauh dari planet (gambar di sudut kiri atas setiap gambar adalah jarak antara pengamat dan planet).

Terlihat bahwa:

awalnya ukuran sudut planet berkurang - ini adalah perspektif langsung yang biasa
kemudian, ketika planet telah melewati garis khatulistiwa dari dunia kita (jarak lebih dari 25), ukuran sudutnya meningkat - ini adalah efek dari perspektif berlawanan yang akrab bagi kita
ketika merangkak ke kutub yang berlawanan dari dunia kita, kita melihat permukaan terbatas (jarak 46.875)
ketika planet ini berada di kutub yang berlawanan dari dunia kita (jarak 50) ia membentang ke seluruh langit
ketika meluncur dari kutub yang berlawanan dari dunia kita, kita melihat permukaan yang terbentang (jarak 53.125)
setelah planet ini melewati kutub yang berlawanan dari dunia kita, ia tampak berubah secara simetris - oktan merah telah berubah dengan warna biru dan seterusnya
kemudian, ukuran sudut planet berkurang (jarak dari 50 ke 75), dan kemudian meningkat (jarak dari 75 ke 100) - ini adalah efek yang dikenal baik dari perspektif maju dan mundur kedua

Artefak. Saat menggunakan model, diketahui bahwa selama perjalanan planet ini melalui titik-titik yang terletak dari pengamat pada jarak 25, 50 dan 75, artefak dapat muncul - wol dapat "tumbuh" di planet ini atau bahkan mungkin "hancur". Rupanya matematika saya tidak memperhitungkan sesuatu)

Gambar planet di sekitar kutub yang berlawanan dari dunia kita ("lensa" sudut lebar digunakan). Permukaan planet di depan kita sangat menyempit - Anda tidak hanya dapat melihat seluruh Belahan Bumi Utara, tetapi juga bagian dari Belahan Bumi Selatan di belakang khatulistiwa. Permukaan planet di belakang kita ini sangat memanjang - Kutub Selatan terlihat jelas. Kedua permukaan membentang ke arah satu sama lain, mencoba untuk membungkus kita dalam cangkang bola dan mengungkapkan kepada kita gambar sebuah planet yang membentang di langit.

Eksperimen di mana pengamat melihat ke atas (angka di sudut kiri atas setiap gambar adalah sudut antara arah ke bawah dan pandangan).

Dalam gambar:

pertama kali muncul cakrawala sisi planet kita
kemudian, kita melihat cakrawala kedua di atasnya, di mana kita menemukan apa yang terletak di sisi planet kita di belakang punggung kita di belakang cakrawala
melihat ke atas, kita melihat bagian belakang planet ini

Gambar cakrawala ganda ("lensa" sudut lebar digunakan). Jalur langit cukup besar karena kita berada di ketinggian sekitar 50 km.

Gambar langit di atas kepala ("lensa" sudut lebar digunakan)

Dunia tanpa malam.
Selanjutnya, untuk kesederhanaan, kita akan menyebut planet kita Bumi, satelit alaminya - Bulan, dan bintang di sekitar mana mereka berputar - Matahari. Proporsi ukuran Matahari, Bumi, Bulan dan orbitnya untuk kejelasan tidak akan diamati.
Dalam gambar: perbatasan antara sisi siang dan malam planet melewati Samudera Atlantik. Pada saat yang sama, Bumi yang memudar dan terus tumbuh terlihat. Orang-orang yang duduk di pangkalan lunar di dunia kita melihat gambaran yang kira-kira sama)

Pada animasi: pergerakan perbatasan antara sisi siang dan malam Bumi. Anda dapat melihat tumpang tindih Matahari dengan piringan Bumi yang diterangi oleh sinar Matahari yang dilepaskan di sepanjang jalan panjang.

Gerhana matahari dan bulan.
Foto: Bulan muncul dari bayang-bayang Bumi. Batas-batas antara sisi siang dan malam Bumi dan Bulan terlihat.

Pada animasi: gerhana matahari dan bulan.

Terlihat bahwa:

pertama, bumi melemparkan bayangan di bulan, dan bulan melemparkan bayangan di bumi
lalu bulan keluar dari bayang-bayang bumi, dan bayang-bayang bulan meninggalkan permukaan bumi
lalu bayangan bulan kembali ke permukaan bumi dan bulan kembali memasuki bayangan bumi
batas antara sisi siang dan malam bulan tidak terlihat ketika bulan ditutupi oleh cakram bumi karena sisi bulan yang menghadap kita masih dalam bayang-bayang Bumi

Pada animasi: pergerakan batas antara sisi siang dan malam Bumi dan Bulan dikombinasikan dengan gerhana matahari dan bulan. Orang-orang yang melayani observatorium di titik Lagrange L ₂ di dunia kita melihat kira-kira gambar yang sama) Tentu saja, jika kita mengabaikan rotasi Bumi)

Foto: fajar tentang ISS di dunia kita)

Kesimpulan

Untuk apa semua ini)? Saya hanya benar-benar ingin melihat dunia melalui mata makhluk yang hidup di alam semesta yang tertutup rapat dengan geometri bola. Untuk mengetahui dunia yang indah ini tanpa simbol-simbol Christoffel dan hal-hal sejenisnya sambil tetap berada dalam kerangka kursus umum matematika yang lebih tinggi. Hasilnya ada di depan Anda. Segalanya tampak berhasil. Semoga Anda memiliki hari yang menarik dan menyenangkan!

Kode sumber .

Model yang berfungsi (buka di PC, bukan untuk perangkat seluler).

Bagi mereka yang tertarik pada subjek, ada artikel yang luar biasa yang berbicara tentang fenomena luar biasa yang dapat diamati di Alam Semesta yang sebenarnya: Cara menggambar lubang hitam. Penelusuran sinar geodesik dalam ruang-waktu melengkung .

Dunia hipersphere tiga dimensi. Penelusuran sinar geodesik di alam semesta tertutup dengan geometri bola

Pendahuluan Dunia tertutup dua dimensi

Dunia tertutup tiga dimensi

Model

Kenalan pertama

Studi visual

Kesimpulan

More articles: