🈶 👻 🤦🏻 Logistik aksi untuk pengumpulan terpisah barang daur ulang 🌞 👨‍🎓 🙎🏻

Alih-alih bergabung

Ketika proses pengumpulan dan pengolahan limbah sepenuhnya disesuaikan di Rusia, tidak mudah untuk mengatakannya, tetapi saya ingin tidak berpartisipasi dalam pengisian kembali tempat pembuangan akhir sekarang. Oleh karena itu, di banyak kota besar, dengan satu atau lain cara, ada gerakan sukarela yang terlibat dalam pengumpulan terpisah.

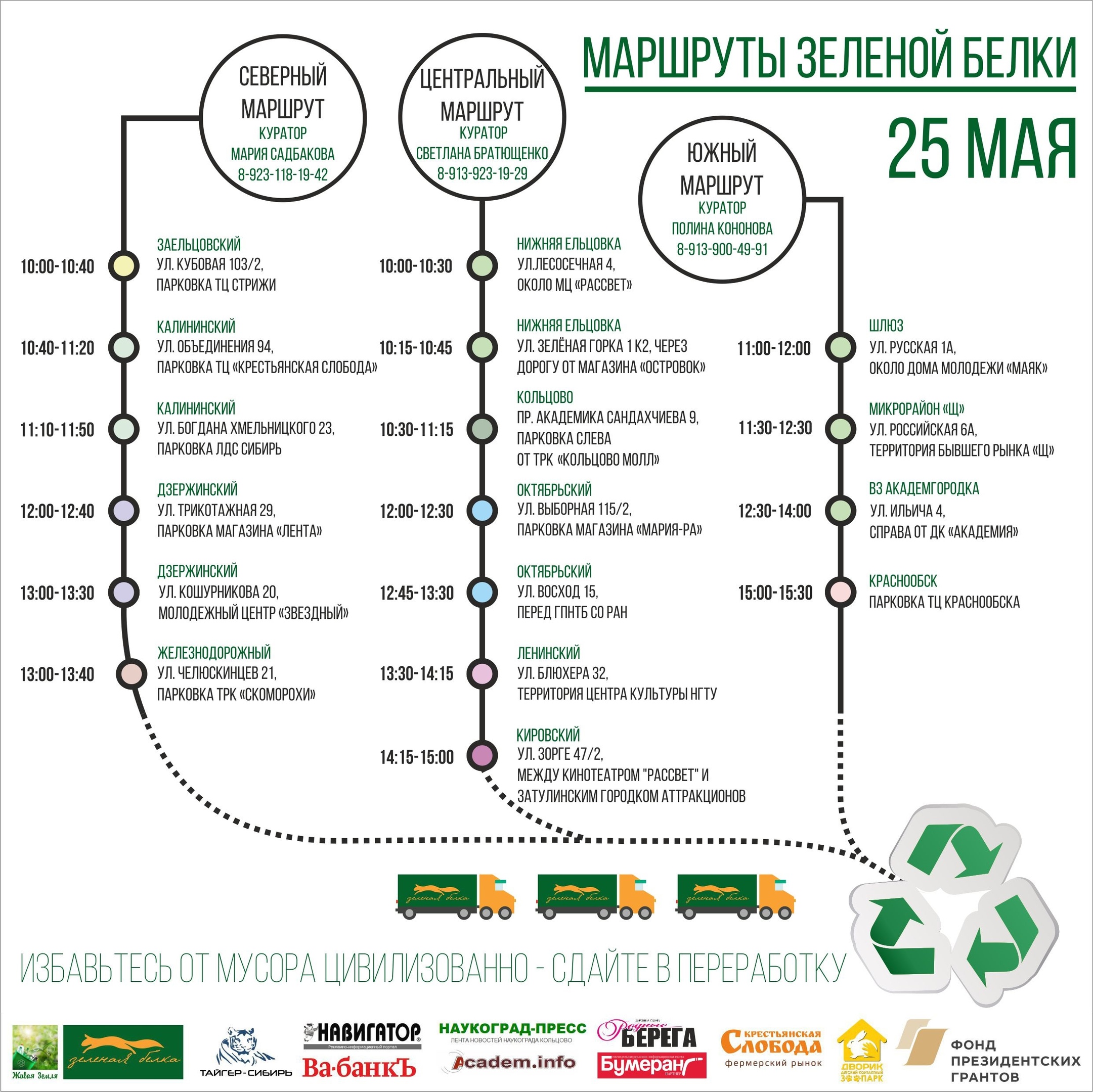
Di Novosibirsk, kegiatan semacam itu dibentuk di sekitar kampanye Green Squirrel, dalam rangka yang sebulan sekali, warga kota yang khawatir tentang lingkungan membawa akumulasi sampah rumah tangga yang dapat didaur ulang ke tempat-tempat yang telah ditentukan pada waktu tertentu. Pada saat yang sama, sebuah truk sewaan tiba di sana, yang membawa barang-barang yang dikumpulkan dan disortir ke lokasi, dari mana ia didistribusikan kembali di antara berbagai perusahaan pemrosesan. Tindakan ini telah ada sejak 2014, dan sejak saat itu jumlah titik pengumpulan untuk daur ulang, serta volumenya, telah meningkat secara signifikan. Untuk rute truk, hanya tatapan saja tidak cukup, dan kami mulai mengembangkan model optimisasi untuk meminimalkan biaya transportasi. Yang pertama dari model ini adalah subjek dari artikel ini.

Di bagian 1, saya akan menjelaskan secara rinci dan dengan ilustrasi skema untuk mengatur tindakan. Selanjutnya, dalam Bagian 2, tugas meminimalkan biaya transportasi akan diformalkan sebagai tugas rute kendaraan heterogen, masalah rute kendaraan armada dengan jendela waktu. Bagian 3 dikhususkan untuk memecahkan masalah ini menggunakan paket yang didistribusikan secara bebas untuk menyelesaikan masalah pemrograman matematika linear integer GLPK.

1. Aksi "Tupai Hijau"

Sejak 2014, kelompok inisiatif Bumi Hidup telah melakukan kampanye bulanan untuk memisahkan koleksi Tupai Hijau daur ulang di Novosibirsk. Pada saat penulisan, daur ulang dengan sejumlah pemesanan diterima limbah plastik berlabel PET, PE, PP, PS, kaca, aluminium, besi, peralatan rumah tangga, kertas limbah dan banyak lagi. Lebih dari 50 relawan berpartisipasi dalam persiapan dan pelaksanaan aksi. Tindakan ini tidak komersial, partisipasi di dalamnya gratis dan tidak menyiratkan hadiah uang.

Poin

Aksi ini diadakan di 17 titik kota, terletak satu sama lain pada jarak yang ditempuh oleh mobil dalam periode 15 hingga 90 menit. Salah satu poin di foto ini: tas di sebelah kiri di sepanjang dinding untuk mengumpulkan berbagai pecahan plastik, di sebelah kanan - sebuah truk, di mana semuanya dimuat di masa depan, dan di tengah - seorang sukarelawan dengan telinga.

gambar

Semua aktivitas pada saat ini diatur oleh kurator yang memiliki batasan waktu di mana mereka siap untuk memenuhi tugas mereka. Ketika merencanakan suatu tindakan, kurator melaporkan interval waktu di mana tindakan harus dilewati pada titik mereka.

Ada juga data tentang volume rata-rata daur ulang yang dikumpulkan di setiap titik.

Rute

Poin diatur dalam rute yang berturut-turut digerakkan oleh truk. Pergerakan truk dipantau oleh pengawas rute yang memantau lingkungan operasional dan membuat keputusan tentang penanganan acara khusus.

gambar

Truk

Apakah disewa secara umum dalam kerangka proposal untuk sewa kendaraan angkutan per jam. Tidak mungkin memadatkan plastik pada tempatnya, oleh karena itu parameter utama yang mencirikan truk adalah volume bak. Daya dukung dalam kasus kami bukan merupakan faktor pembatas.

Biaya utama tindakan terkait dengan pembayaran sewa truk, oleh karena itu, pengurangannya sangat penting untuk keberadaan dan pengembangan bagian kami, yang memperoleh signifikansi institusional dalam arti membentuk gagasan tentang konsumsi yang bertanggung jawab. Selanjutnya, pendekatan untuk memecahkan masalah ini akan dijelaskan, berdasarkan penerapan metode optimasi diskrit, yaitu, pemrograman matematika.

2. Formalisasi

Dalam membangun model matematika, kita akan tetap berada dalam kerangka program linear-integer campuran, yang pemahaman pengetahuan aljabar kelas 7 sudah cukup.

Satu-satunya kesulitan dapat dikaitkan dengan penggunaan notasi abstrak dan tanda penjumlahan dalam formula. Saya harap ini tidak menakut-nakuti pembaca yang jarang bertemu dengan teks matematika.

Dalam model optimisasi, empat komponen dapat dibedakan:

pembentukan kelompok titik yang membentuk rute terpisah;
definisi skema jalan memutar untuk masing-masing kelompok;
memenuhi persyaratan untuk saat kedatangan truk di setiap titik;
penentuan jenis truk yang dibutuhkan untuk melayani setiap rute.

Kami mempertimbangkan masing-masing bagian, memperkenalkan notasi yang diperlukan sebagaimana diperlukan.

Pengelompokan poin

Biarkan

V = \ {1, \ dots, n \}

$V = \ {1, \ dots, n \}$ ada banyak indeks titik pengumpulan untuk bahan-bahan yang dapat didaur ulang, dan situs tempat pengumpulan yang dapat didaur ulang kemudian diangkut - kita akan menyebutnya depot - memiliki indeks 0. Masukkan

\ bar {V} = V \ cup \ {0 \}

$\ bar {V} = V \ cup \ {0 \}$

Setiap kelompok titik membentuk rute terpisah. Melalui

R

$R$ menunjukkan himpunan nomor rute.

Biarkan kuantitasnya

z_{i r}, i d i I, r d i R

$z_ {ir}, i \ di I, r \ di R$ sama dengan satu jika intinya

i

$i$ termasuk dalam rute dengan nomor tersebut

r

$r$ , dan nol jika tidak. Maka syarat itulah intinya

i d a l a m V

$i \ dalam V$ harus memasukkan salah satu rute yang dapat ditulis sebagai

s u m_{r d a l a m R} z_{i r} = z_{i 1} + z_{i 2} + d o t s + z_{i n} = 1.

$\ sum_ {r \ dalam R} z_ {ir} = z_ {i1} + z_ {i2} + \ dots + z_ {in} = 1.$

Depot harus memasukkan semua rute:

z_{0 r} = 1, r d a l a m R

$z_ {0r} = 1, r \ dalam R$

Kehalusan

Sayangnya, catatan seperti itu menciptakan masalah komputasi yang terkait dengan simetri wilayah yang diizinkan. Ini dapat dihilangkan dengan menambahkan sejumlah pembatasan memastikan pilihan dekomposisi minimal leksikografis. Anda dapat membaca lebih lanjut tentang ini dalam bahasa Rusia, misalnya, di sini .

1 - z_{i r} l e q s u m_{j = 1}^{i - 1} k i r i (1 - s u m_{k = 1}^{r - 1} z_{j k} k a n a n) + s u m_{k = 1}^{r - 1} z_{i k}, q u a d i d i I, r d i R, r l e q i .

$1-z_ {ir} \ leq \ sum_ {j = 1} ^ {i-1} \ kiri (1- \ sum_ {k = 1} ^ {r-1} z_ {jk} \ kanan) + \ sum_ { k = 1} ^ {r-1} z_ {ik}, \ quad i \ di I, r \ di R, r \ leq i.$

Definisi jalan memutar

Rute adalah urutan titik dan persimpangan yang bergantian di antara keduanya. Secara resmi, mereka semua mulai di salah satu titik set

V

$V$ dan berakhir di depot, bagaimanapun, akan lebih mudah untuk mengasumsikan bahwa semua rute bersifat siklik. Asumsi ini tidak mengubah esensi, tetapi membuat semua simpul sama: dalam hal ini tidak ada simpul ujung, mereka semua transit.

Untuk poin

i, j i n b a r V

$i, j \ in \ bar {V}$ dan rute

r i n R

$r \ in R$ mengatur variabel

x_{i j r}

$x_ {ijr}$ sama dengan satu jika dalam rute dengan angka

r

$r$ truk bergerak dari titik

i

$i$ to the point

j

$j$ , dan nol jika tidak.

Maka kita perlu, pertama, bahwa truk bergerak di sepanjang rute

r i n R

$r \ in R$ mengunjungi titik

i d a l a m V

$i \ dalam V$ jika dia, setelah membaginya menjadi kelompok-kelompok, jatuh ke dalam kelompok dengan nomor tersebut

r

$r$ :

s u m_{j d a l a m b a r V} x_{j i r} = z_{i r}, q u a d i i n b a r V, r d a l a m R .

$\ sum_ {j \ dalam \ bar {V}} x_ {jir} = z_ {ir}, \ quad i \ in \ bar {V}, r \ dalam R.$

Kedua, truk setelah sampai di titik

i i n b a r V

$i \ in \ bar {V}$ harus meninggalkannya.

s u m_{j d i b a r V} x_{j i r} = s u m_{j i n b a r V} x_{i j r}, q u a d i d i b a r V, r d a l a m R .

$\ sum_ {j \ di \ bar {V}} x_ {jir} = \ sum_ {j \ in \ bar {V}} x_ {ijr}, \ quad i \ di \ bar {V}, r \ dalam R .$

Anda mungkin memperhatikan bahwa pembatasan ini memungkinkan kuantitas

x_{i j r}

$x_ {ijr}$ Tentukan rute yang merupakan himpunan loop terpisah. Rute seperti ini, tentu saja, tidak masuk akal, dan sejumlah pembatasan diperlukan untuk menghindarinya.

Tentang menghilangkan sub-sepeda

Salah satu cara bisa dengan memperkenalkan jumlah non-negatif tambahan

f_{i j r}, i, j d i b a r V, r d a l a m R

$f_ {ijr}, i, j \ di \ bar {V}, r \ dalam R$ Himpunan relasi yang direkam menggunakan kuantitas ini menghilangkan kombinasi nilai

x_{i j r}

$x_ {ijr}$ mendefinisikan rute yang bukan merupakan loop yang terhubung.

s u m_{i i n V} f_{0 j r} = s u m_{i i n V} z_{i r}, q u a d r d a l a m R,

$\ sum_ {i \ in V} f_ {0jr} = \ sum_ {i \ in V} z_ {ir}, \ quad r \ dalam R,$

f_{i j r} l e q n x_{i j r}, q u a d i i n b a r V, j i n b a r V, r d a l a m R,

$f_ {ijr} \ leq nx_ {ijr}, \ quad i \ in \ bar {V}, j \ in \ bar {V}, r \ dalam R,$

s u m_{j i n b a r V} f_{j i r} = s u m_{j i n b a r V} f_{i j r} + z_{i r}, q u a d i d a l a m V, r i n R .

$\ sum_ {j \ in \ bar {V}} f_ {jir} = \ sum_ {j \ in \ bar {V}} f_ {ijr} + z_ {ir}, \ quad i \ dalam V, r \ in R.$

Rasio-rasio ini menentukan aliran dari depot ke seluruh titik rute. Pada setiap titik tengah, satu unit aliran diserap, sehingga agar jaringan memiliki aliran daya yang sama dengan jumlah titik minus satu, rute harus dihubungkan.

Memenuhi persyaratan pada saat kedatangan truk di setiap titik

Dengan kata lain, Anda harus mengunjungi titik hanya di dalam jendela waktu yang ditunjukkan oleh kurator. Melalui

B_{i}

$B_i$ dan

E_{i}

$E_i$ menunjukkan, masing-masing, awal dan akhir interval waktu di mana kurator titik

i

$i$ boleh hadir.

Untuk melacak implementasi pembatasan ini, kami memerlukan informasi tentang waktu yang dihabiskan truk selama halte dan penyeberangan di rute. Melalui

L_{i}, i d a l a m V

$L_i, i \ dalam V$ menunjukkan durasi pemuatan pada titik tersebut

i

$i$ , dan melalui

D_{i j}, i, j i n b a r V

$D_ {ij}, i, j \ in \ bar {V}$ - waktu bergerak dari satu titik

i

$i$ to the point

j

$j$ Kami membuat reservasi itu

D_{0 i} = 0

$D_ {0i} = 0$ untuk semua

i i n b a r V

$i \ in \ bar {V}$ , dan umumnya dapat dilakukan

D_{i j} n e q D_{j i}

$D_ {ij} \ neq D_ {ji}$ untuk apa saja

i n e q j

$i \ neq j$

Kami memperkenalkan variabel non-negatif

a_{i}, i i n b a r V

$a_i, i \ in \ bar {V}$ dan

w_{i r}, i d i b a r V, r d a l a m R

$w_ {ir}, i \ di \ bar {V}, r \ dalam R$ sama dengan waktu kedatangan dan waktu tunggu di titik

i

$i$ saat mengemudi di sepanjang rute

r

$r$ masing-masing. Untuk nilai yang dimasukkan, hubungan berikut harus dipenuhi.

Waktu tunggu tidak kurang dari waktu yang dibutuhkan untuk memuat

w_{i r} g e q L_{i} z_{i r}, q u a d i i n b a r V, r d a l a m R,

$w_ {ir} \ geq L_iz_ {ir}, \ quad i \ in \ bar {V}, r \ dalam R,$

dan sama dengan nol jika titik tersebut bukan milik rute

r

$r$

w_{i r} l e q M z_{i r}, q u a d i i n b a r V, r d a l a m R,

$w_ {ir} \ leq Mz_ {ir}, \ quad i \ in \ bar {V}, r \ dalam R,$

Waktu tiba di titik

j

$j$ dihitung pada waktu yang tepat untuk poin sebelumnya

i

$i$ Berikut adalah konstanta yang cukup besar

M

$M$ digunakan untuk menghilangkan dependensi yang tidak perlu saat berpindah

i

$i$ dan

j

$j$ belum selesai.

a_{i} + s u m_{r i n R} w_{i r} + D_{i j} l e q a_{j} + M (1 - s u m_{r i n R} x_{i j r}), q u a d i i n I, j d a l a m V,

$a_i + \ sum_ {r \ in R} w_ {ir} + D_ {ij} \ leq a_j + M (1 - \ sum_ {r \ in R} x_ {ijr}), \ quad i \ in I, j \ dalam V,$

Kedatangan dan keberangkatan truk harus dalam interval yang ditunjukkan oleh kurator.

a_{i} g e q B_{i}, q u a d i d a l a m V,

$a_i \ geq B_i, \ quad i \ dalam V,$

a_{i} + s u m_{r d a l a m R} w_{i r} l e q E_{i}, q u a d i d a l a m V .

$a_i + \ sum_ {r \ dalam R} w_ {ir} \ leq E_i, \ quad i \ dalam V.$

Menentukan jenis truk yang dibutuhkan untuk melayani setiap rute
Nyatakan banyak jenis truk yang dapat disewa oleh

T

$T$ Jenis truk

t d a l a m T

$t \ dalam T$ ditandai dengan volume tubuh

C_{t}

$C_t$ dan biaya sewa satu jam

P_{t}

$P_t$ Waktu sewa truk minimum

t

$t$ dilambangkan dengan

U_{t}^{0}

$U_t ^ 0$ Jumlah daur ulang yang dikumpulkan pada saat itu

i d a l a m V

$i \ dalam V$ dilambangkan dengan

G_{i}

$G_i$

Kami memperkenalkan variabel

y_{t r}, t d i T, r d a l a m R

$y_ {tr}, t \ di T, r \ dalam R$ sama dengan satu jika jenis truk

t

$t$ ditugaskan ke rute layanan dengan nomor

r

$r$ , dan nol jika tidak.

Variabel integer

u_{t r}, t d i T, r d a l a m R

$u_ {tr}, t \ di T, r \ dalam R$ mengatur waktu menyewa jenis truk

t

$t$ melayani rute dengan nomor

r

$r$
Untuk setiap rute,

r i n R

$r \ in R$ , Anda harus menetapkan jenis truk:

s u m_{t d a l a m T} y_{t r} = 1, q u a d r d a l a m R

$\ sum_ {t \ dalam T} y_ {tr} = 1, \ quad r \ dalam R$

Sesuai dengan rincian titik di antara rute, beberapa rute mungkin menjadi sepele, yaitu hanya berisi depo. Jika rute

r

$r$ non-sepele, maka truk yang ditugaskan kepadanya setidaknya disewa

U_{t}^{0}

$U_t ^ 0$ jam.

u_{t r} g e q U_{t}^{0} (y_{t r} - s u m_{i i n V} z_{i r}), q u a d t d i T, r d a l a m R .

$u_ {tr} \ geq U_t ^ 0 (y_ {tr} - \ sum_ {i \ in V} z_ {ir}), \ quad t \ di T, r \ dalam R.$

Pada saat yang sama, durasi sewa juga harus melebihi total durasi parkir dan bergerak di sepanjang rute.

u_{t r} g e q s u m_{i d i V} s u m_{j i n b a r V} D_{i j} x_{i j r} + s u m_{i d i b a r V} w_{i r} - M (1 - y_{t r}), q u a d r i n R, t i n T .

$u_ {tr} \ geq \ sum_ {i \ di V} \ sum_ {j \ in \ bar {V}} D_ {ij} x_ {ijr} + \ sum_ {i \ di \ bar {V}} w_ { ir} -M (1-y_ {tr}), \ quad r \ in R, t \ in T.$

Tambahkan batasan yang menyediakan properti: jika truk berjenis

t

$t$ tidak ditugaskan ke rute

r

$r$ , waktu sewanya nol.

u_{t r} l e q M y_{t r} .

$u_ {tr} \ leq My_ {tr}.$

Semua daur ulang yang dikumpulkan di titik-titik rute harus sesuai di belakang truk.

s u m_{i d a l a m V} G_{i} z_{i r} l e q s u m_{t d a l a m T} C_{t} y_{t r}, q u a d r d a l a m R .

$\ sum_ {i \ dalam V} G_iz_ {ir} \ leq \ sum_ {t \ dalam T} C_ty_ {tr}, \ quad r \ dalam R.$

Akhirnya, tujuan kami adalah untuk meminimalkan biaya sewa truk, yang, dengan menggunakan sebutan yang diperkenalkan, ditulis sebagai

s u m_{t i n T} s u m_{r i n R} P_{t} u_{t r}

$\ sum_ {t \ in T} \ sum_ {r \ in R} P_tu_ {tr}$

Cari solusinya

Sangat mudah untuk memverifikasi bahwa semua ekspresi yang terlibat dalam model optimasi adalah fungsi linear dari variabel, oleh karena itu, untuk menemukan solusi yang tepat dan perkiraan, Anda dapat menggunakan paket standar untuk menyelesaikan masalah pemrograman bilangan bulat seperti Gurobi , CPLEX , Xpress , ORtools , SCIP , BLIS , dll.
Kami menulis model untuk meminimalkan biaya transportasi dalam bahasa GMPL. Ini akan memungkinkan kita untuk menggunakan paket GLPK gratis untuk tujuan kita. Untuk menulis kode dan men-debug model, akan lebih mudah untuk mengunduh lingkungan pengembangan GUSEK , yang sudah mengandung GLPK dalam komposisinya.

GUSEK terlihat seperti ini:

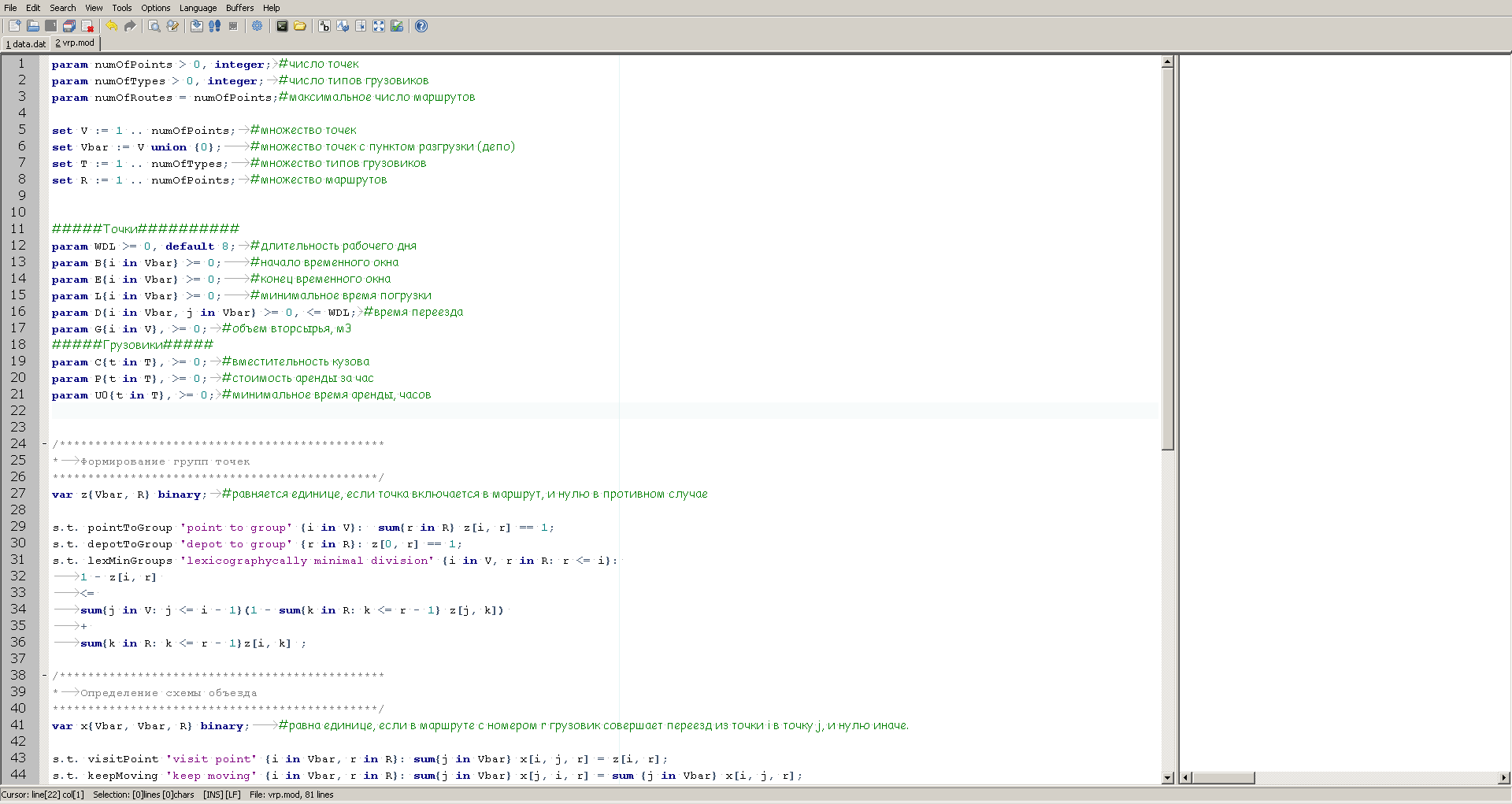
gambar

Di sebelah kiri kita melihat deskripsi model, dan di sebelah kanan ada jendela untuk menampilkan informasi tentang kemajuan perhitungan, yang akan disediakan oleh pemecah setelah peluncuran.

Deskripsi lengkap model

param numOfPoints > 0, integer; #  param numOfTypes > 0, integer; #   param numOfRoutes = numOfPoints;#   set V := 1 .. numOfPoints; #  set Vbar := V union {0}; #     () set T := 1 .. numOfTypes; #   set R := 1 .. numOfPoints; #  ############### param WDL >= 0, default 8; #   param B{i in Vbar} >= 0; #   param E{i in Vbar} >= 0; #   param L{i in Vbar} >= 0; #   param D{i in Vbar, j in Vbar} >= 0, <= WDL; #  param G{i in V}, >= 0; # , 3 ########## param C{t in T}, >= 0; #  param P{t in T}, >= 0; #    param U0{t in T}, >= 0; #  ,  /********************************************** *    **********************************************/ var z{Vbar, R} binary; # ,     ,      st pointToGroup 'point to group' {i in V}: sum{r in R} z[i, r] == 1; st depotToGroup 'depot to group' {r in R}: z[0, r] == 1; st lexMinGroups 'lexicographycally minimal division' {i in V, r in R: r <= i}: 1 - z[i, r] <= sum{j in V: j <= i - 1}(1 - sum{k in R: k <= r - 1} z[j, k]) + sum{k in R: k <= r - 1}z[i, k] ; /********************************************** *    **********************************************/ var x{Vbar, Vbar, R} binary; # ,    c  r      i   j,   . st visitPoint 'visit point' {i in Vbar, r in R}: sum{j in Vbar} x[i, j, r] = z[i, r]; st keepMoving 'keep moving' {i in Vbar, r in R}: sum{j in Vbar} x[j, i, r] = sum {j in Vbar} x[i, j, r]; var f{Vbar, Vbar, R} >= 0; #,  . st flowFromDepot 'flow from depot' {r in R}: sum{i in V} f[0, i, r] == sum{i in V} z[i, r]; st flowAlongActiveArcs 'flow along active arcs' {i in Vbar, j in Vbar, r in R}: f[i, j, r] <= numOfPoints * x[i, j, r]; st flowConservation 'flow conservation' {i in V, r in R}: sum{j in Vbar} f[j, i, r] == sum{j in Vbar} f[i, j, r] + z[i, r]; var a{i in V} >= 0; #     var w{i in Vbar, r in R} >= 0; #     st wait 'wait'{i in Vbar, r in R}: w[i, r] >= L[i] * z[i, r]; st dontWait 'dont wait'{i in Vbar, r in R}: w[i, r] <= (E[i] - B[i]) * z[i, r]; st arrivalTime 'arrival time' {i in V, j in V}: a[i] + sum{r in R}w[i, r] + D[i,j] <= a[j] + 3 * WDL * (1 - sum{r in R} x[i, j, r]); st arriveAfter 'arrive after' {i in V}: a[i] >= B[i]; st departBefore 'depart before' {i in V}: a[i] + sum{r in R}w[i, r] <= E[i]; /********************************************** *   ,       **********************************************/ var y{t in T, r in R}, binary; # ,    t       r,   . var u{t in T, r in R}, integer, >= 0; #    t,     rst assignVehicle 'assign vehicle' {r in R}: sum{t in T} y[t,r] == 1; st rentTime 'rent time' {r in R, t in T}: u[t, r] >= sum{i in V, j in Vbar}D[i, j] * x[i, j, r] + sum{i in Vbar}w[i, r] - WDL * (1 - y[t, r]); st minRentTime 'minimal rent time' {r in R, t in T}: u[t, r] >= U0[t] * (y[t, r] - sum{i in V}z[i, r]); st noRent 'no rent' {t in T, r in R}: u[t, r] <= WDL * y[t, r]; st fitCapacity 'fit capacity' {r in R}: sum{i in V} G[i] * z[i, r] <= sum{t in T} C[t] * y[t, r]; minimize rentCost: sum{t in T, r in R} P[t] * u[t, r]; solve; /********************************************** *     **********************************************/ printf{i in V, r in R} (if 0.1 < z[i,r] then "point %s to group %s\n" else ""), i, r, z[i,r]; printf{r in R, i in Vbar, j in Vbar} (if 0.1 < x[i, j, r] then "route %s: %s -> %s\n" else ""), r, i, j; printf{i in V} "point %s arrive between %s and %s (actual = %s)\n", i, B[i], E[i], a[i]; end;

Untuk memulai lebih cepat, saya juga akan menambahkan data yang diambil dari kepala saya yang disiapkan untuk digunakan dalam model:

Masukkan data

 data; param numOfPoints := 9; #  param numOfTypes := 6; #   ############### param : B E L := 0 0 8 1 1 0 8 1 2 0 8 1 3 0 8 1 4 0 8 1 5 0 8 1 6 0 8 1 7 0 8 1 8 0 8 1 9 0 8 1; param D default 0 : 0 1 2 3 4 5 6 7 8 9 := 0 . . . . . . . . . . 1 0.1 0.3 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 2 0.3 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 3 0.4 0.3 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 4 0.4 0.4 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 5 0.1 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 6 0.5 0.5 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 7 0.3 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 8 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 9 0.5 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1; param G := 1 1 2 2 3 1 4 2 5 1 6 2 7 1 8 2 9 1; ########## param : C P := 1 8 500 2 10 500 3 14 600 4 18 650 5 25 700 6 35 800; param U0 default 2; #  ,  end;

Setelah menyalin kode model ke file dengan nama, misalnya, model.mod, dan memasukkan data ke file data.dat, semuanya siap dijalankan. Kami menetapkan batas pada waktu perhitungan 100 detik (ini dilakukan dengan menggunakan kunci --tmlim [waktu dalam detik]), mentransfer path ke file dengan data input (menggunakan key -d [path file]),

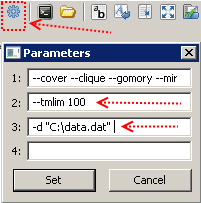
gambar

dan tekan F5. Jika berhasil, pesan akan muncul di jendela di sebelah kanan, dan setelah seratus detik kita akan memiliki solusi terbaik yang berhasil ditemukan GLPK dalam waktu yang ditentukan.

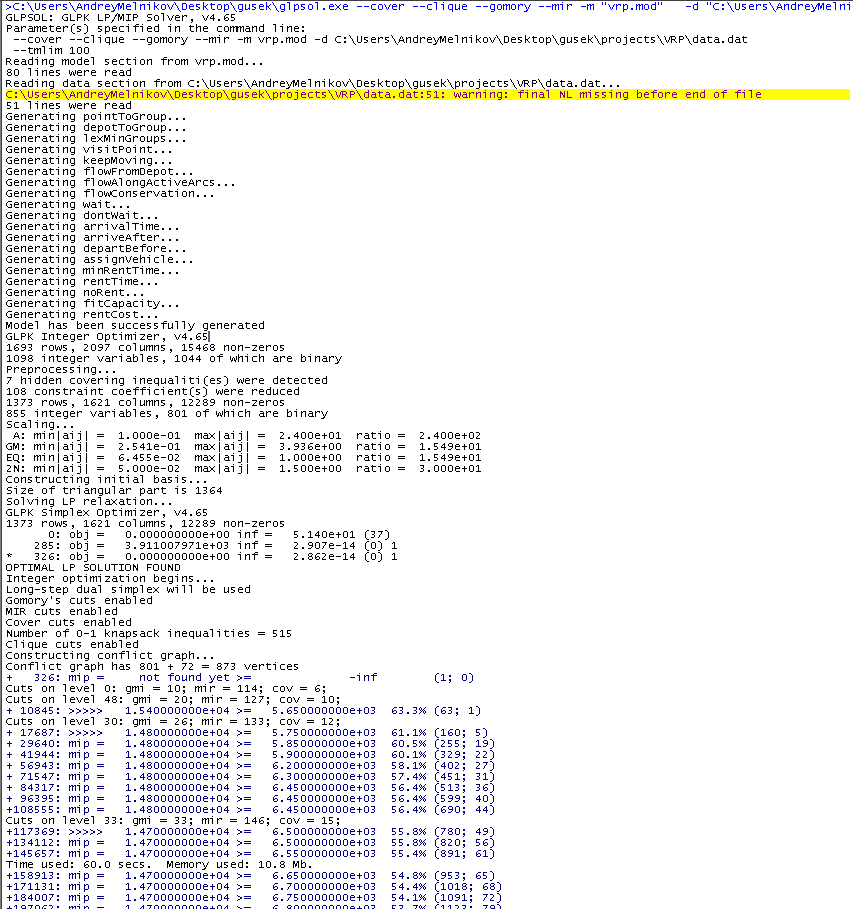
gambar

Dalam teks biru, kami tertarik pada makna setelah tulisan "mip =". Seperti yang Anda lihat, itu berkurang dari waktu ke waktu. Semua solusi baru sedang dalam proses kerja, nilai biaya transportasi yang terbaik ditampilkan di kolom ini (ada 14700 sejauh ini). Angka berikutnya adalah batas bawah untuk solusi terbaik yang ada, yaitu solusi optimal . Awalnya, perkiraan ini secara signifikan diremehkan, tetapi disempurnakan dari waktu ke waktu, yaitu meningkat. Nilai-nilai di sebelah kiri dan di sebelah kanan adalah konvergen, dan kesenjangan relatif di antara mereka pada saat screenshot adalah 54,1%. Segera setelah angka ini menjadi nol, algoritma akan membuktikan bahwa solusi terbaik yang ditemukan adalah yang terbaik. Tidak selalu dibenarkan untuk menunggu acara ini dalam praktek, dan tidak hanya karena itu adalah waktu yang lama, tetapi penting untuk membuat reservasi bahwa, sebagai suatu peraturan, solusi yang baik relatif cepat, dan biaya waktu utama dikaitkan dengan penyempurnaan estimasi yang diperlukan untuk membuktikan yang terbaik.

Alih-alih sebuah kesimpulan

Masalah rute sangat kompleks secara komputasi, dan dengan peningkatan jumlah titik yang perlu dikunjungi, waktu yang diperlukan bagi seorang pemecah untuk menemukan solusi dan membuktikan optimalitasnya berkembang pesat. Namun, untuk contoh yang cukup kecil, dalam jumlah waktu yang wajar, pemecah mampu membangun serangkaian rute yang sukses dan dapat digunakan untuk mendukung pengambilan keputusan. Analisis opsi perutean yang diusulkan oleh model membantu kami menemukan peluang signifikan untuk pengurangan biaya, dan ini sangat penting untuk keberadaan dan pengembangan stok.

Upaya kami selanjutnya menuju pekerjaan dengan ketidakpastian dalam volume daur ulang yang dikumpulkan di titik-titik tersebut. Kami sedang mengembangkan sejumlah model pemrograman stokastik untuk membuat keputusan strategis dan operasional dalam rute truk. Jika topiknya ternyata relevan dan membangkitkan minat, saya akan menulis tentang hal ini juga, karena sebentar lagi kita semua harus secara signifikan menyelami lebih dalam isu-isu lingkungan, yang ingin saya sukseskan.

Logistik aksi untuk pengumpulan terpisah barang daur ulang

Alih-alih bergabung

1. Aksi "Tupai Hijau"

2. Formalisasi

Cari solusinya

Alih-alih sebuah kesimpulan

More articles: