Jaringan saraf dan pembelajaran mendalam, bab 1: menggunakan jaringan saraf untuk mengenali angka tulisan tangan

Catatan

Berikut ini adalah terjemahan buku online gratis Michael Nielsen, Neural Networks dan Deep Learning, yang didistribusikan di bawah Lisensi Creative Commons Attribution-NonCommercial 3.0 Unported . Motivasi untuk penciptaannya adalah pengalaman sukses menerjemahkan buku teks pemrograman, JavaScript Ekspresif . Buku tentang jaringan saraf juga cukup populer, penulis artikel berbahasa Inggris secara aktif mengutipnya. Saya tidak menemukan terjemahannya, kecuali terjemahan awal bab pertama dengan singkatan .

Mereka yang ingin berterima kasih kepada penulis buku dapat melakukan ini di halaman resminya , dengan mentransfer melalui PayPal atau Bitcoin. Untuk mendukung penerjemah di Habré ada formulir "untuk mendukung penulis".

Pendahuluan

Tutorial ini akan memberi tahu Anda secara rinci tentang konsep-konsep seperti:

• Jaringan saraf - paradigma perangkat lunak yang sangat baik, dibuat di bawah pengaruh biologi, dan memungkinkan komputer untuk belajar berdasarkan pengamatan.
• Pembelajaran mendalam adalah seperangkat teknik pelatihan jaringan saraf yang kuat.

Neural networks (NS) dan deep learning (GO) saat ini memberikan solusi terbaik untuk banyak masalah di bidang pengenalan gambar, suara dan pemrosesan bahasa alami. Tutorial ini akan mengajarkan Anda banyak konsep kunci yang mendukung NS dan GO.

Tentang apa buku ini

NS adalah salah satu paradigma perangkat lunak terbaik yang pernah ditemukan oleh manusia. Dengan pendekatan pemrograman standar, kami memberi tahu komputer apa yang harus dilakukan, memecah tugas-tugas besar menjadi banyak tugas kecil, dan secara tepat menentukan tugas yang akan dilakukan dengan mudah oleh komputer. Dalam kasus Majelis Nasional, sebaliknya, kami tidak memberi tahu komputer bagaimana menyelesaikan masalah. Dia sendiri belajar ini berdasarkan "pengamatan" data, "menciptakan" solusi sendiri untuk masalah tersebut.

Pembelajaran berbasis data otomatis terdengar menjanjikan. Namun, hingga 2006, kami tidak tahu bagaimana melatih Majelis Nasional sehingga mereka dapat melampaui pendekatan yang lebih tradisional, dengan pengecualian beberapa kasus khusus. Pada tahun 2006, teknik pelatihan disebut deep neural networks (GNS). Sekarang teknik ini dikenal dengan deep learning (GO). Mereka terus dikembangkan, dan hari ini GNS dan GO telah mencapai hasil luar biasa dalam banyak tugas penting yang terkait dengan visi komputer, pengenalan ucapan, dan pemrosesan bahasa alami. Dalam skala besar, mereka dikerahkan oleh perusahaan seperti Google, Microsoft dan Facebook.

Tujuan buku ini adalah untuk membantu Anda menguasai konsep-konsep kunci jaringan saraf, termasuk teknik GO modern. Setelah bekerja dengan tutorial, Anda akan menulis kode yang menggunakan NS dan GO untuk memecahkan masalah pengenalan pola yang kompleks. Anda akan memiliki dasar untuk menggunakan NS dan pertahanan sipil dalam pendekatan untuk menyelesaikan masalah Anda sendiri.

Pendekatan Berbasis Prinsip

Salah satu keyakinan yang mendasari buku ini adalah bahwa lebih baik memperoleh pemahaman yang kuat tentang prinsip-prinsip utama Majelis Nasional dan Masyarakat Sipil daripada mengambil pengetahuan dari daftar panjang berbagai ide. Jika Anda memiliki pemahaman yang baik tentang ide-ide kunci, Anda akan dengan cepat memahami materi baru lainnya. Dalam bahasa programmer, kita dapat mengatakan bahwa kita akan mempelajari sintaks dasar, pustaka, dan struktur data dari bahasa baru. Anda mungkin mengenali hanya sebagian kecil dari keseluruhan bahasa - banyak bahasa memiliki pustaka standar yang sangat besar - namun, Anda dapat memahami pustaka dan struktur data baru dengan cepat dan mudah.

Jadi, buku ini jelas bukan materi pendidikan tentang cara menggunakan perpustakaan tertentu untuk Majelis Nasional. Jika Anda hanya ingin belajar cara bekerja dengan perpustakaan - jangan membaca buku! Temukan perpustakaan yang Anda butuhkan dan kerjakan dengan materi pelatihan dan dokumentasi. Namun perlu diingat: walaupun pendekatan ini memiliki keuntungan dalam memecahkan masalah secara instan, jika Anda ingin memahami apa yang sebenarnya terjadi di dalam Majelis Nasional, jika Anda ingin menguasai ide-ide yang relevan dalam beberapa tahun, maka tidak akan cukup bagi Anda untuk hanya mempelajari semacam perpustakaan mode. Anda perlu memahami ide-ide jangka panjang yang andal dan mendasari pekerjaan Majelis Nasional. Teknologi datang dan pergi, dan gagasan bertahan lama.

Pendekatan praktis

Kami akan mempelajari prinsip-prinsip dasar dengan contoh tugas tertentu: mengajar komputer untuk mengenali angka tulisan tangan. Menggunakan pendekatan pemrograman tradisional, tugas ini sangat sulit untuk diselesaikan. Namun, kita dapat menyelesaikannya dengan cukup baik dengan NS sederhana dan beberapa lusin baris kode, tanpa perpustakaan khusus. Selain itu, kami secara bertahap akan meningkatkan program ini, secara konsisten termasuk di dalamnya semakin banyak gagasan utama tentang Majelis Nasional dan Pertahanan Sipil.

Pendekatan praktis ini berarti bahwa Anda akan memerlukan beberapa pengalaman pemrograman. Tetapi Anda tidak harus menjadi programmer profesional. Saya menulis kode python (versi 2.7) yang harus jelas bahkan jika Anda belum menulis program python. Dalam proses belajar, kami akan membuat perpustakaan kami sendiri untuk Majelis Nasional, yang dapat Anda gunakan untuk eksperimen dan pelatihan lebih lanjut. Semua kode dapat diunduh di sini . Setelah menyelesaikan buku, atau dalam proses membaca, Anda dapat memilih salah satu perpustakaan yang lebih lengkap untuk Majelis Nasional, disesuaikan untuk digunakan dalam proyek-proyek ini.

Persyaratan matematika untuk memahami materi cukup rata-rata. Sebagian besar bab memiliki bagian matematika, tetapi biasanya mereka adalah aljabar dasar dan grafik fungsi. Kadang-kadang saya menggunakan matematika yang lebih maju, tetapi saya menyusun materi sehingga Anda dapat memahaminya, bahkan jika beberapa detail menghindari Anda. Sebagian besar matematika digunakan dalam bab 2, yang memerlukan sedikit matanalisis dan aljabar linier. Bagi mereka yang belum mereka kenal, saya memulai Bab 2 dengan pengantar matematika. Jika Anda merasa kesulitan, lewati saja bab ini sampai pembekalan. Bagaimanapun, jangan khawatir tentang ini.

Buku jarang berorientasi pada pemahaman prinsip-prinsip dan pendekatan praktis. Tetapi saya percaya bahwa lebih baik belajar berdasarkan ide-ide dasar Majelis Nasional. Kami akan menulis kode kerja, dan tidak hanya mempelajari teori abstrak, dan Anda dapat menjelajahi dan memperluas kode ini. Dengan cara ini, Anda akan memahami dasar-dasarnya, baik teori maupun praktik, dan akan dapat belajar lebih lanjut.

Latihan dan Tugas

Penulis buku teknis sering memperingatkan pembaca bahwa ia hanya perlu menyelesaikan semua latihan dan menyelesaikan semua masalah. Ketika membaca peringatan seperti itu kepada saya, mereka selalu tampak sedikit aneh. Akankah sesuatu yang buruk terjadi pada saya jika saya tidak melakukan latihan dan menyelesaikan masalah? Tidak, tentu saja Saya hanya akan menghemat waktu dengan pemahaman yang kurang mendalam. Terkadang itu sepadan. Terkadang tidak.

Apa yang pantas dilakukan dengan buku ini? Saya menyarankan Anda untuk mencoba menyelesaikan sebagian besar latihan, tetapi jangan mencoba untuk menyelesaikan sebagian besar tugas.

Sebagian besar latihan perlu diselesaikan karena ini adalah pemeriksaan dasar untuk pemahaman materi yang tepat. Jika Anda tidak dapat melakukan latihan dengan relatif mudah, Anda harus melewatkan sesuatu yang mendasar. Tentu saja, jika Anda benar-benar terjebak dalam suatu jenis latihan - jatuhkan, mungkin ini adalah semacam kesalahpahaman kecil, atau mungkin saya memiliki sesuatu yang buruk dirumuskan. Tetapi jika sebagian besar latihan menyebabkan Anda kesulitan, maka kemungkinan besar Anda perlu membaca ulang materi sebelumnya.

Tugas adalah masalah lain. Mereka lebih sulit daripada latihan, dan dengan beberapa Anda akan mengalami kesulitan. Ini menjengkelkan, tetapi tentu saja kesabaran dalam menghadapi kekecewaan seperti itu adalah satu-satunya cara untuk benar-benar memahami dan menyerap subjek.

Jadi saya tidak menyarankan menyelesaikan semua masalah. Lebih baik lagi - ambil proyek Anda sendiri. Anda mungkin ingin menggunakan NS untuk mengklasifikasikan koleksi musik Anda. Atau untuk memprediksi nilai saham. Atau yang lainnya. Tetapi temukan proyek yang menarik untuk Anda. Dan kemudian Anda dapat mengabaikan tugas-tugas dari buku, atau menggunakannya murni sebagai inspirasi untuk mengerjakan proyek Anda. Masalah dengan proyek Anda sendiri akan mengajarkan Anda lebih dari bekerja dengan sejumlah tugas. Keterlibatan emosional adalah faktor kunci dalam penguasaan prestasi.

Tentu saja, sementara Anda mungkin tidak memiliki proyek seperti itu. Ini normal. Selesaikan tugas yang membuat Anda merasakan motivasi intrinsik. Gunakan bahan dari buku untuk membantu Anda menemukan ide untuk proyek kreatif pribadi.

Bab 1

Sistem visual manusia adalah salah satu keajaiban dunia. Pertimbangkan urutan nomor tulisan tangan berikut:



Kebanyakan orang akan membacanya dengan mudah, seperti 504192. Tetapi kesederhanaan ini menipu. Di setiap belahan otak, seseorang memiliki korteks visual primer , juga dikenal sebagai V1, yang berisi 140 juta neuron dan puluhan miliar koneksi di antara mereka. Pada saat yang sama, tidak hanya V1 yang terlibat dalam penglihatan manusia, tetapi seluruh rangkaian wilayah otak - V2, V3, V4 dan V5 - yang terlibat dalam pemrosesan gambar yang semakin kompleks. Kami membawa di kepala kami sebuah superkomputer yang ditala oleh evolusi selama ratusan juta tahun, dan diadaptasi dengan sempurna untuk memahami dunia yang terlihat. Mengenali nomor tulisan tangan tidaklah mudah. Hanya saja kita, orang-orang, luar biasa, sangat baik, mengenali apa yang mata kita tunjukkan kepada kita. Tetapi hampir semua pekerjaan ini dilakukan secara tidak sadar. Dan biasanya kami tidak menganggap penting tugas yang sulit diselesaikan oleh sistem visual kami.

Kesulitan mengenali pola visual menjadi jelas ketika Anda mencoba menulis program komputer untuk mengenali angka-angka seperti yang di atas. Apa yang tampaknya mudah dalam eksekusi kami tiba-tiba ternyata sangat kompleks. Konsep sederhana tentang bagaimana kita mengenali bentuk - "kesembilan memiliki lingkaran di atas dan bar vertikal di kanan bawah" - sama sekali tidak begitu sederhana untuk ekspresi algoritmik. Dengan mencoba mengartikulasikan aturan-aturan ini dengan jelas, Anda dengan cepat terjebak dalam rawa pengecualian, perangkap, dan acara-acara khusus. Tugas itu tampaknya tidak ada harapan.

Pendekatan NS untuk memecahkan masalah dengan cara yang berbeda. Idenya adalah untuk mengambil banyak angka tulisan tangan yang dikenal sebagai contoh pengajaran,



dan kembangkan sistem yang dapat belajar dari contoh-contoh ini. Dengan kata lain, Majelis Nasional menggunakan contoh untuk secara otomatis membuat aturan pengakuan angka tulisan tangan. Selain itu, dengan menambah jumlah contoh pelatihan, jaringan dapat mempelajari lebih lanjut tentang angka tulisan tangan dan meningkatkan akurasinya. Jadi, walaupun saya telah mengutip di atas hanya 100 studi kasus, mungkin kita dapat membuat sistem pengenalan tulisan tangan yang lebih baik menggunakan ribuan atau bahkan jutaan dan milyaran studi kasus.

Dalam bab ini kita akan menulis sebuah program komputer yang mengimplementasikan pembelajaran NS untuk mengenali angka tulisan tangan. Program ini akan hanya sepanjang 74 baris, dan tidak akan menggunakan perpustakaan khusus untuk Majelis Nasional. Namun, program singkat ini akan dapat mengenali angka tulisan tangan dengan akurasi lebih dari 96%, tanpa memerlukan campur tangan manusia. Selain itu, dalam bab-bab selanjutnya kami akan mengembangkan gagasan yang dapat meningkatkan akurasi hingga 99% atau lebih. Bahkan, NS komersial terbaik melakukan pekerjaan dengan baik sehingga digunakan oleh bank untuk memproses cek, dan layanan pos untuk mengenali alamat.

Kami berkonsentrasi pada pengenalan tulisan tangan, karena ini merupakan prototipe tugas untuk mempelajari NS. Prototipe seperti itu sangat ideal bagi kami: ini adalah tugas yang sulit (mengenali nomor tulisan tangan bukanlah tugas yang mudah), tetapi tidak begitu rumit sehingga membutuhkan solusi yang sangat kompleks atau daya komputasi yang sangat besar. Selain itu, ini adalah cara yang bagus untuk mengembangkan teknik yang lebih kompleks, seperti GO. Karena itu, dalam buku ini kita akan terus kembali ke tugas pengenalan tulisan tangan. Nanti kita akan membahas bagaimana ide-ide ini dapat diterapkan pada tugas-tugas lain dari visi komputer, pengenalan suara, pemrosesan bahasa alami dan bidang lainnya.

Tentu saja, jika tujuan bab ini hanya untuk menulis program untuk mengenali angka tulisan tangan, maka bab itu akan jauh lebih pendek! Namun, dalam prosesnya, kami akan mengembangkan banyak ide kunci yang terkait dengan NS, termasuk dua jenis neuron buatan ( perceptron dan sigmoid neuron), dan algoritma pembelajaran NS standar, keturunan gradien stokastik . Dalam teks, saya berkonsentrasi menjelaskan mengapa semuanya dilakukan dengan cara ini, dan pada pembentukan pemahaman Anda tentang Majelis Nasional. Ini membutuhkan percakapan yang lebih lama daripada jika saya baru saja mempresentasikan mekanika dasar tentang apa yang terjadi, tetapi membutuhkan pemahaman yang lebih dalam yang akan Anda miliki. Di antara kelebihan lainnya - di akhir bab ini Anda akan memahami apa pertahanan sipil dan mengapa pertahanan itu begitu penting.

Perceptrons

Apa itu jaringan saraf? Untuk memulai, saya akan berbicara tentang satu jenis neuron buatan yang disebut perceptron. Perceptrons diciptakan oleh ilmuwan Frank Rosenblatt pada 1950-an dan 60-an, terinspirasi oleh karya awal Warren McCallock dan Walter Pitts . Saat ini, model lain dari neuron buatan lebih sering digunakan - dalam buku ini, dan sebagian besar karya modern di NS terutama menggunakan model sigmoid dari neuron. Kami akan segera bertemu dengannya. Tetapi untuk memahami mengapa neuron sigmoid didefinisikan dengan cara ini, perlu menghabiskan waktu menganalisis perceptron.

Jadi bagaimana cara kerja perceptrons? Perceptron menerima beberapa angka biner x ₁ , x ₂ , ... dan memberikan satu angka biner:



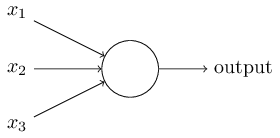
Dalam contoh ini, perceptron memiliki tiga angka input, x ₁ , x ₂ , x ₃ . Secara umum, mungkin ada lebih atau kurang dari mereka. Rosenblatt mengusulkan aturan sederhana untuk menghitung hasilnya. Dia memperkenalkan bobot, w ₁ , w ₂ , bilangan real, yang menyatakan pentingnya bilangan input yang sesuai untuk hasil. Output dari neuron, 0 atau 1, ditentukan oleh apakah jumlah tertimbang kurang atau lebih dari ambang tertentu [ambang batas] $$$\ sum_j w_jx_j$ . Seperti bobot, ambang adalah bilangan real, parameter dari neuron. Dalam istilah matematika:

$$

$$output = \ begin {cases} 0 ~ if ~ \ sum_j w_jx_j \ leq threshold \\ 1 ~ jika ~ \ sum_j w_jx_j> threshold \ end {cases} \ tag {1}$$

Itulah keseluruhan deskripsi perceptron!

Ini adalah model matematika dasar. Sebuah perceptron dapat dianggap sebagai pengambil keputusan dengan menimbang bukti. Biarkan saya memberi Anda contoh yang tidak terlalu realistis, tetapi sederhana. Katakanlah akhir pekan akan datang, dan Anda mendengar bahwa festival keju akan diadakan di kota Anda. Anda suka keju, dan mencoba memutuskan apakah akan pergi ke festival atau tidak. Anda dapat mengambil keputusan dengan menimbang tiga faktor:

1. Apakah cuacanya bagus?
2. Apakah pasangan Anda ingin pergi dengan Anda?
3. Apakah festival jauh dari transportasi umum? (Anda tidak punya mobil).

Ketiga faktor ini dapat direpresentasikan sebagai variabel biner x ₁ , x ₂ , x ₃ . Misalnya, x ₁ = 1 jika cuacanya bagus, dan 0 jika cuacanya buruk. x ₂ = 1 jika pasangan Anda ingin pergi, dan 0 jika tidak. Sama untuk x ₃ .

Sekarang, katakanlah Anda penggemar berat keju sehingga Anda siap untuk pergi ke festival, bahkan jika pasangan Anda tidak tertarik padanya dan sulit untuk mendapatkannya. Tapi mungkin Anda hanya membenci cuaca buruk, dan jika cuaca buruk, Anda tidak akan pergi ke festival. Anda dapat menggunakan perceptrons untuk memodelkan proses pengambilan keputusan seperti itu. Salah satu caranya adalah dengan memilih bobot w ₁ = 6 untuk cuaca, dan w ₂ = 2, w ₃ = 2 untuk kondisi lainnya. Nilai lebih besar dari w1 berarti bahwa cuaca lebih penting bagi Anda daripada apakah pasangan Anda akan bergabung dengan Anda atau kedekatan festival untuk berhenti. Akhirnya, misalkan Anda memilih ambang batas 5 untuk perceptron. Dengan opsi ini, perceptron mengimplementasikan model keputusan yang diinginkan, memberikan 1 ketika cuaca bagus dan 0 saat buruk. Keinginan pasangan dan kedekatan berhenti tidak mempengaruhi nilai output.

Dengan mengubah bobot dan ambang, kita bisa mendapatkan model pengambilan keputusan yang berbeda. Sebagai contoh, katakanlah kita mengambil ambang batas 3. Kemudian perceptron memutuskan bahwa Anda perlu pergi ke festival, baik ketika cuaca bagus, atau ketika festival berada di dekat halte bus dan pasangan Anda setuju untuk pergi bersama Anda. Dengan kata lain, modelnya berbeda. Menurunkan ambang berarti Anda ingin lebih ke festival.

Jelas, perceptron bukanlah model pengambilan keputusan manusia yang lengkap! Tetapi contoh ini menunjukkan bagaimana perceptron dapat menimbang berbagai jenis bukti untuk membuat keputusan. Tampaknya mungkin bahwa jaringan perceptron yang kompleks dapat membuat keputusan yang sangat kompleks:



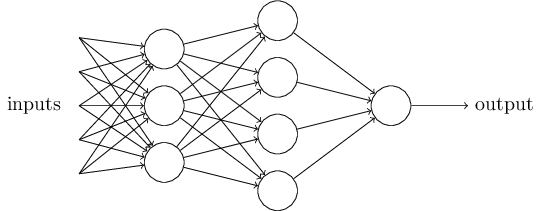
Dalam jaringan ini, kolom pertama dari perceptrons - yang kita sebut lapisan pertama perceptrons - membuat tiga keputusan yang sangat sederhana, menimbang bukti input. Bagaimana dengan perceptrons dari lapisan kedua? Masing-masing dari mereka membuat keputusan, menimbang hasil dari lapisan pengambilan keputusan pertama. Dengan cara ini, perceptron dari lapisan kedua dapat membuat keputusan pada tingkat yang lebih kompleks dan abstrak dibandingkan dengan perceptron dari lapisan pertama. Dan bahkan keputusan yang lebih kompleks dapat dibuat oleh perceptrons di lapisan ketiga.Dengan cara ini, jaringan perceptron yang lebih berlapis dapat menangani keputusan yang rumit.

Omong-omong, ketika saya menentukan perceptron, saya mengatakan bahwa ia hanya memiliki satu nilai output. Tetapi dalam jaringan di atas, perceptrons terlihat seperti mereka memiliki beberapa nilai output. Padahal, mereka hanya punya satu jalan keluar. Banyak panah keluaran hanya cara mudah untuk menunjukkan bahwa keluaran perceptron digunakan sebagai input dari beberapa perceptron lainnya. Ini kurang rumit daripada menggambar keluar bercabang tunggal.

Mari sederhanakan deskripsi perceptrons. Ketentuan$$Σ j dari w j x j > t r e s h o l d canggung, dan kita bisa menyepakati dua perubahan untuk rekaman kesederhanaannya. Yang pertama adalah merekam$\sum_j w_jx_j > treshold$$$∑ j w j x j sebagai produk skalar,$\sum_j w_jx_j$$$w ⋅ x = ∑ j w j x j , di mana w dan x adalah vektor yang komponennya masing-masing adalah bobot dan data input. Yang kedua adalah untuk mentransfer ambang batas ke bagian lain dari ketidaksetaraan, dan menggantinya dengan nilai yang dikenal sebagai perceptron displacement [bias],$w \cdot x = \sum_j w_jx_j$$$$b \equiv −threshold$ . Menggunakan perpindahan alih-alih ambang batas, kita dapat menulis ulang aturan perceptron:

$$

$$output = \begin{cases} 0 ~ if ~ w \cdot x + b \leq 0 \\ 1 ~ if ~ w \cdot x + b > 0 \end{cases} \tag{2}$$

Offset dapat direpresentasikan sebagai ukuran betapa mudahnya untuk mendapatkan nilai 1 pada output dari perceptron. Atau, dalam istilah biologis, perpindahan adalah ukuran seberapa mudahnya untuk mengaktifkan perceptron. Sebuah perceptron dengan bias yang sangat besar sangat mudah untuk diberikan 1. Tetapi dengan bias negatif yang sangat besar, ini sulit dilakukan. Jelas, pengenalan bias adalah perubahan kecil dalam deskripsi perceptrons, tetapi kemudian kita akan melihat bahwa itu mengarah pada penyederhanaan lebih lanjut dari rekaman. Oleh karena itu, lebih lanjut kami tidak akan menggunakan ambang, tetapi akan selalu menggunakan offset.

Saya menggambarkan perceptrons dalam hal metode menimbang bukti untuk pengambilan keputusan. Metode lain penggunaannya adalah perhitungan fungsi logis elementer, yang biasanya kita anggap sebagai perhitungan utama, seperti AND, OR dan NAND. Misalkan, misalnya, kita memiliki perceptron dengan dua input, bobot masing-masing adalah -2, dan offsetnya adalah 3. Ini dia: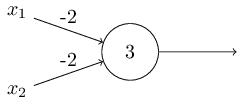



Input 00 memberikan output 1, karena (−2) ∗ 0 + (- 2 ) ∗ 0 + 3 = 3 lebih besar dari nol. Perhitungan yang sama mengatakan bahwa input 01 dan 10 memberikan 1. Tetapi 11 pada input memberikan 0 pada output, karena (−2) ∗ 1 + (- 2) ∗ 1 + 3 = −1, kurang dari nol. Karena itu, perceptron kami mengimplementasikan fungsi NAND!

Contoh ini menunjukkan bahwa perceptrons dapat digunakan untuk menghitung fungsi logika dasar. Bahkan, kita dapat menggunakan jaringan perceptron untuk menghitung fungsi logis apa saja secara umum. Faktanya adalah bahwa gerbang logika NAND bersifat universal untuk perhitungan - dimungkinkan untuk membangun perhitungan apa pun pada dasarnya. Misalnya, Anda dapat menggunakan gerbang NAND untuk membuat sirkuit yang menambahkan dua bit, x ₁ dan x ₂ . Untuk melakukan ini, hitung jumlah bitwise$$x 1 ⊕ x 2 , sertaflag carry, yaitu 1 ketika x₁dan x₂adalah 1 - yaitu, flag carry hanyalah hasil penggandaan bitwise x₁x₂:Untuk mendapatkan jaringan yang setara dari perceptrons, kami mengganti semua Gerbang NAND adalah perceptrons dengan dua input, berat masing-masing adalah -2, dan dengan offset 3. Berikut ini adalah jaringan yang dihasilkan. 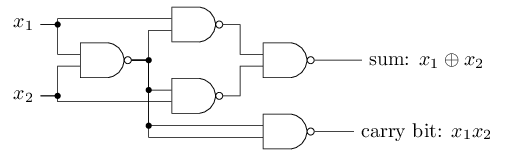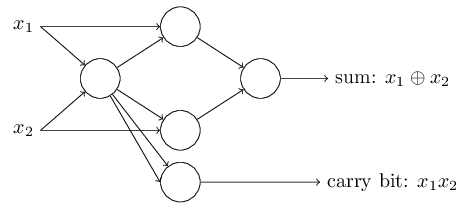Perhatikan bahwa saya memindahkan perceptron yang sesuai dengan katup kanan bawah, hanya untuk membuatnya lebih mudah untuk menggambar panah:$x_1 \oplus x_2$







Satu aspek penting dari jaringan perceptron ini adalah bahwa output dari jaringan yang paling kiri digunakan dua kali sebagai input ke bagian bawah. Mendefinisikan model perceptron, saya tidak menyebutkan diterimanya skema keluar ganda di tempat yang sama. Padahal, itu tidak terlalu penting. Jika kita tidak ingin mengizinkan ini, kita cukup menggabungkan dua garis dengan bobot -2 menjadi satu dengan bobot -4. (Jika ini tidak terlihat jelas bagi Anda, berhentilah dan buktikan sendiri). Setelah perubahan ini, jaringan terlihat sebagai berikut, dengan semua bobot yang tidak terisi sama dengan -2, semua offset sama dengan 3, dan satu bobot -4 ditandai:



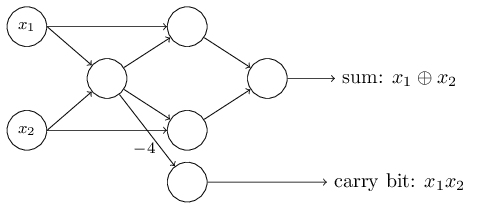Catatan perceptron yang memiliki output tetapi tidak ada input:



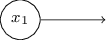hanyalah sebuah singkatan. Ini tidak berarti bahwa dia tidak memiliki input. Untuk memahami ini, anggaplah kita memiliki perceptron tanpa input. Kemudian tertimbang jumlah Σ _j dari w _j x _j akan selalu menjadi nol, sehingga Perceptron akan menghasilkan 1 untuk b> 0 dan 0 untuk b ≤ 0. Artinya, Perceptron hanya akan memberi nilai tetap, tetapi tidak perlu bagi kita (x ₁ Contoh di atas). Lebih baik untuk mempertimbangkan input perceptrons bukan sebagai perceptrons, tetapi sebagai unit khusus yang hanya didefinisikan sehingga menghasilkan nilai yang diinginkan x ₁ , x ₂ , ...

Contoh penambah menunjukkan bagaimana jaringan perceptron dapat digunakan untuk mensimulasikan rangkaian yang berisi banyak gerbang NAND. Dan karena gerbang ini bersifat universal untuk perhitungan, maka perceptron bersifat universal untuk perhitungan.

Fleksibilitas komputasi dari perceptrons cukup menggembirakan dan mengecewakan. Ini menggembirakan, memastikan bahwa jaringan perceptron dapat sekuat perangkat komputasi lainnya. Mengecewakan, memberi kesan bahwa perceptrons hanyalah tipe baru dari gerbang logika NAND. Penemuan begitu-begitu!

Namun, situasinya sebenarnya lebih baik. Ternyata kita dapat mengembangkan algoritma pelatihan yang dapat secara otomatis menyesuaikan bobot dan perpindahan jaringan dari neuron buatan. Penyesuaian ini terjadi sebagai respons terhadap rangsangan eksternal, tanpa intervensi langsung dari seorang programmer. Algoritma pembelajaran ini memungkinkan kita untuk menggunakan neuron buatan dengan cara yang sangat berbeda dari gerbang logika biasa. Alih-alih secara eksplisit mendaftarkan sirkuit dari gerbang NAND dan lainnya, jaringan saraf kita dapat dengan mudah belajar bagaimana menyelesaikan masalah, kadang-kadang yang sangat sulit untuk secara langsung merancang sirkuit reguler.

Neuron Sigmoid

Algoritma pembelajaran sangat bagus. Namun, bagaimana cara mengembangkan algoritma seperti itu untuk jaringan saraf? Misalkan kita memiliki jaringan perceptron yang ingin kita gunakan untuk melatih kita dalam memecahkan suatu masalah. Misalkan input ke jaringan mungkin piksel dari gambar yang dipindai dari digit tulisan tangan. Dan kami ingin jaringan mengetahui bobot dan offset yang dibutuhkan untuk mengklasifikasikan angka-angka dengan benar. Untuk memahami bagaimana pelatihan semacam itu dapat bekerja, mari kita bayangkan bahwa kita sedikit mengubah bobot (atau bias) tertentu dalam jaringan. Kami ingin perubahan kecil ini mengarah ke perubahan kecil dalam output jaringan. Seperti yang akan segera kita lihat, properti ini memungkinkan pembelajaran. Secara skematis, kami ingin yang berikut ini (jelas, jaringan seperti itu terlalu sederhana untuk mengenali tulisan tangan!):



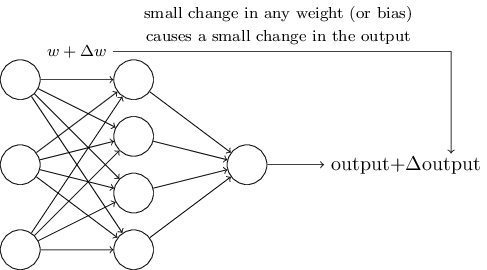
Jika perubahan kecil dalam berat (atau bias) akan menyebabkan perubahan kecil dalam hasil output, kita bisa mengubah bobot dan bias sehingga jaringan kita berperilaku sedikit lebih dekat dengan apa yang kita inginkan. Misalnya, katakanlah jaringan secara tidak benar menetapkan gambar ke "8", meskipun seharusnya "9". Kita bisa mencari cara bagaimana membuat perubahan kecil dalam berat dan perpindahan sehingga jaringan menjadi sedikit lebih dekat dengan mengklasifikasikan gambar sebagai "9". Dan kemudian kita akan mengulangi ini, mengubah bobot dan bergeser lagi dan lagi untuk mendapatkan hasil terbaik dan terbaik. Jaringan akan belajar.

Masalahnya adalah bahwa jika ada perceptrons di jaringan, ini tidak terjadi. Perubahan kecil dalam bobot atau perpindahan perceptron apa pun kadang-kadang dapat menyebabkan perubahan dalam outputnya menjadi sebaliknya, katakanlah, dari 0 menjadi 1. Balik seperti itu dapat mengubah perilaku sisa jaringan dengan cara yang sangat rumit. Dan bahkan jika sekarang "9" kita dikenali dengan benar, perilaku jaringan dengan semua gambar lain mungkin telah sepenuhnya berubah dengan cara yang sulit dikendalikan. Karena itu, sulit untuk membayangkan bagaimana kita dapat secara bertahap menyesuaikan bobot dan offset sehingga jaringan secara bertahap mendekati perilaku yang diinginkan. Mungkin ada beberapa cara pintar untuk mengatasi masalah ini. Tetapi tidak ada solusi sederhana untuk masalah mempelajari jaringan perceptrons.

Masalah ini dapat diatasi dengan memperkenalkan jenis baru neuron buatan yang disebut neuron sigmoid. Mereka mirip dengan perceptrons, tetapi dimodifikasi sehingga perubahan kecil dalam bobot dan offset hanya menghasilkan perubahan kecil pada output. Ini adalah fakta dasar yang akan memungkinkan jaringan neuron sigmoid untuk belajar.

Biarkan saya menggambarkan neuron sigmoid. Kami akan menggambar mereka dengan cara yang sama seperti perceptrons:



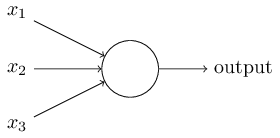
Ini memiliki input yang sama x ₁ , x ₂ , ... Tetapi alih-alih sama dengan 0 atau 1, input ini dapat memiliki nilai apa pun dalam kisaran dari 0 hingga 1. Misalnya, nilai 0,638 akan menjadi input yang valid untuk neuron sigmoid (CH). Sama seperti perceptron, SN memiliki bobot untuk setiap input, w ₁ , w ₂ , ... dan total bias b. Tetapi nilai outputnya tidak akan 0 atau 1. Ini akan menjadi σ (w⋅x + b), di mana σ adalah sigmoid.

By the way, σ kadang-kadang disebut fungsi logistik , dan kelas neuron ini disebut neuron logistik. Sangat berguna untuk mengingat terminologi ini, karena istilah ini digunakan oleh banyak orang yang bekerja dengan jaringan saraf. Namun, kami akan mematuhi terminologi sigmoid.

Fungsi didefinisikan sebagai berikut:

$$

$$\ sigma (z) \ equiv \ frac {1} {1 + e ^ {- z}} \ tag {3}$$

Dalam kasus kami, nilai output dari neuron sigmoid dengan data input x ₁ , x ₂ , ... dengan bobot w ₁ , w ₂ , ... dan offset b akan dianggap sebagai:

$$

$$\ frac {1} {1 + exp (- \ sum_j w_jx_j - b)} \ tag {4}$$

Pada pandangan pertama, CH tampak sama sekali tidak seperti neuron. Tampilan aljabar dari sigmoid mungkin tampak membingungkan dan tidak jelas jika Anda tidak terbiasa dengannya. Sebenarnya, ada banyak kesamaan antara perceptrons dan SN, dan bentuk aljabar dari sigmoid ternyata lebih merupakan detail teknis daripada hambatan serius untuk memahami.

Untuk memahami kesamaan dengan model perceptron, anggaplah bahwa z ≡ w ⋅ x + b adalah angka positif yang besar. Maka e - z ≈ 0, oleh karena itu, σ (z) ≈ 1. Dengan kata lain, ketika z = w ⋅ x + b adalah besar dan positif, hasil SN adalah sekitar 1, seperti dalam perceptron. Misalkan z = w ⋅ x + b besar dengan tanda minus. Kemudian e - z → ∞, dan σ (z) ≈ 0. Jadi untuk z besar dengan tanda minus, perilaku SN juga mendekati perceptron. Dan hanya ketika w ⋅ x + b memiliki ukuran rata-rata, penyimpangan serius dari model perceptron diamati.

Bagaimana dengan bentuk aljabar σ? Bagaimana kita memahaminya? Sebenarnya, bentuk persis σ tidak begitu penting - bentuk fungsi pada grafik itu penting. Ini dia:



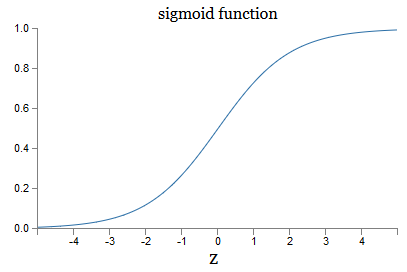
Ini adalah versi lancar dari fungsi langkah:



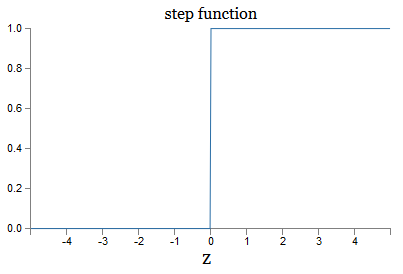
Jika σ adalah stepwise, maka SN akan menjadi perceptron, karena itu akan memiliki 0 atau 1 output tergantung pada tanda w ⋅ x + b (well, pada kenyataannya, pada z = 0, perceptron memberikan 0, dan fungsi langkah - 1 , jadi pada titik itu, fungsinya harus diubah).

Menggunakan fungsi nyata σ, kita mendapatkan perceptron yang dihaluskan. Dan hal utama di sini adalah kelancaran fungsi, bukan bentuk pastinya. Kelancaran berarti bahwa perubahan kecil dengan bobot dan offset willb akan memberikan perubahan kecil put keluaran output. Aljabar memberi tahu kita bahwa putoutput diperkirakan dengan baik sebagai berikut:

$$

$$\ Delta output \ approx \ sum_j \ frac {\ output parsial} {\ partial w_j} \ Delta w_j + \ frac {\ output parsial} {\ partial b} \ Delta b \ tag {5}$$

Jika penjumlahannya melebihi semua bobot _wj , dan ∂output / ∂w _j dan ∂output / ∂b masing-masing menunjukkan turunan parsial dari output sehubungan dengan _j dan b, masing-masing. Jangan panik jika Anda merasa tidak aman di perusahaan turunan pribadi! Meskipun rumusnya terlihat rumit, dengan semua turunan parsial ini, ia sebenarnya mengatakan sesuatu yang sangat sederhana (dan bermanfaat): putoutput adalah fungsi linier tergantung pada bobot dan bias Δw _j dan Δb. Lineritasnya membuatnya mudah untuk memilih perubahan kecil dalam bobot dan offset untuk mencapai bias output kecil yang diinginkan. Jadi, meskipun SN mirip dengan persepsi dalam perilaku kualitatif, mereka membuatnya lebih mudah untuk memahami bagaimana output dapat diubah dengan mengubah bobot dan perpindahan.

Jika bentuk umum σ penting bagi kita, dan bukan bentuk tepatnya, lalu mengapa kita menggunakan rumus seperti itu (3)? Bahkan, nanti kita kadang-kadang akan mempertimbangkan neuron yang outputnya adalah f (w ⋅ x + b), di mana f () adalah beberapa fungsi aktivasi lainnya. Hal utama yang berubah ketika fungsi berubah adalah nilai turunan parsial dalam persamaan (5). Ternyata ketika kita menghitung turunan parsial ini, penggunaan σ sangat menyederhanakan aljabar, karena eksponen memiliki sifat yang sangat bagus ketika membedakan. Bagaimanapun, σ sering digunakan dalam bekerja dengan jaringan saraf, dan paling sering dalam buku ini kita akan menggunakan fungsi aktivasi seperti itu.

Bagaimana menafsirkan hasil kerja CH? Jelas, perbedaan utama antara perceptrons dan CH adalah bahwa CH tidak hanya memberikan 0 atau 1. Outputnya dapat berupa bilangan real dari 0 hingga 1, sehingga nilai seperti 0,173 atau 0,689 valid. Ini dapat bermanfaat, misalnya, jika Anda ingin nilai output menunjukkan, misalnya, kecerahan rata-rata piksel gambar yang diterima pada input NS. Tapi kadang-kadang bisa merepotkan. Misalkan kita ingin keluaran jaringan mengatakan bahwa "gambar 9 adalah input" atau "input gambar bukan 9". Jelas, akan lebih mudah jika nilai output 0 atau 1, seperti perceptron. Namun dalam praktiknya, kita dapat sepakat bahwa nilai output minimal 0,5 akan berarti "9" pada input, dan nilai apa pun yang kurang dari 0,5 akan berarti bahwa itu "bukan 9". Saya akan selalu secara eksplisit menunjukkan keberadaan perjanjian tersebut.

Latihan

• CH mensimulasikan perceptrons, bagian 1

Misalkan kita mengambil semua bobot dan offset dari jaringan perceptrons, dan mengalikannya dengan konstanta positif c> 0. Tunjukkan bahwa perilaku jaringan tidak berubah.

• CH mensimulasikan perceptrons, bagian 2

Misalkan kita memiliki situasi yang sama seperti pada masalah sebelumnya - jaringan perceptrons. Juga anggaplah bahwa input data untuk jaringan dipilih. Kami tidak membutuhkan nilai tertentu, yang utama adalah tetap. Misalkan bobot dan perpindahan sedemikian rupa sehingga w⋅x + b ≠ 0, di mana x adalah nilai input dari setiap perceptron jaringan. Sekarang kita mengganti semua perceptrons dalam jaringan dengan SN, dan gandakan bobot dan perpindahan dengan konstanta positif c> 0. Tunjukkan bahwa dalam batas c → ∞ perilaku jaringan dari SN akan persis sama dengan jaringan perceptrons. Bagaimana pernyataan ini dilanggar jika untuk salah satu dari perceptrons w⋅x + b = 0?

Arsitektur jaringan saraf

Pada bagian selanjutnya, saya akan memperkenalkan jaringan saraf yang mampu mengklasifikasikan angka tulisan tangan dengan baik. Sebelum itu, ada baiknya menjelaskan terminologi yang memungkinkan kita untuk menunjuk ke bagian jaringan yang berbeda. Katakanlah kita memiliki jaringan berikut:



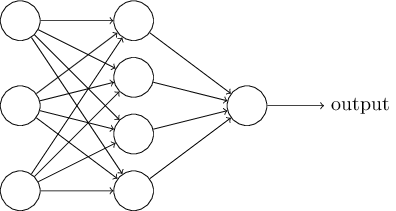
Seperti yang saya sebutkan, lapisan paling kiri dalam jaringan disebut lapisan input, dan neuronnya disebut neuron input. Lapisan paling kanan, atau keluaran, berisi neuron keluaran, atau, seperti dalam kasus kami, satu neuron keluaran. Lapisan tengah disebut tersembunyi, karena neuronnya bukan input maupun output. Istilah "tersembunyi" mungkin terdengar sedikit misterius - ketika saya pertama kali mendengarnya, saya memutuskan bahwa itu harus memiliki kepentingan filosofis atau matematika yang mendalam - namun, itu hanya berarti "tidak masuk atau keluar." Jaringan di atas hanya memiliki satu lapisan tersembunyi, tetapi beberapa jaringan memiliki beberapa lapisan tersembunyi. Misalnya, dalam jaringan empat lapis berikut ini ada dua lapisan tersembunyi:



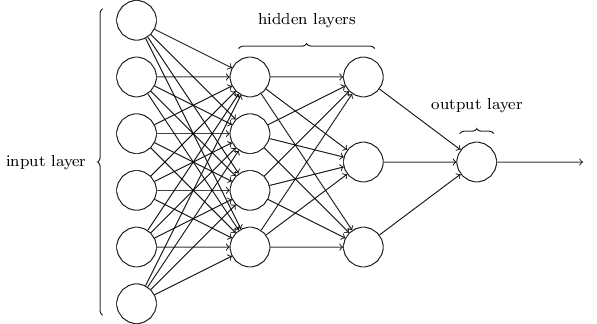
Ini mungkin membingungkan, tetapi karena alasan historis, jaringan multi-layer seperti itu kadang-kadang disebut multilayer perceptrons, MLPs, meskipun mereka terdiri dari neuron sigmoid daripada perceptron. Saya tidak akan menggunakan terminologi seperti itu karena membingungkan, tetapi saya harus memperingatkan tentang keberadaannya.

Mendesain layer input dan output terkadang merupakan tugas yang sederhana. Sebagai contoh, katakanlah kita mencoba menentukan apakah angka tulisan tangan berarti "9" atau tidak. Sirkuit jaringan alami akan menyandikan kecerahan piksel gambar dalam neuron input. Jika gambar hitam dan putih dengan ukuran 64x64 piksel, maka kita akan memiliki 64x64 = 4096 neuron input, dengan kecerahan dalam kisaran dari 0 hingga 1. Lapisan output hanya akan berisi satu neuron, yang nilainya kurang dari 0,5 akan berarti bahwa "pada input bukan 9 ", tetapi nilai lebih akan berarti bahwa" input adalah 9 ".

Dan sementara mendesain layer input dan output seringkali merupakan tugas yang sederhana, mendesain layer tersembunyi bisa menjadi seni yang sulit. Secara khusus, tidak mungkin untuk menggambarkan proses pengembangan lapisan tersembunyi dengan beberapa aturan praktis sederhana. Para peneliti Majelis Nasional telah mengembangkan banyak aturan heuristik untuk desain lapisan tersembunyi yang membantu untuk mendapatkan perilaku jaringan saraf yang diinginkan. Misalnya, heuristik semacam itu dapat digunakan untuk memahami bagaimana mencapai kompromi antara jumlah lapisan tersembunyi dan waktu yang tersedia untuk melatih jaringan. Nanti kita akan menemui beberapa aturan ini.

Sejauh ini, kita telah membahas NS di mana output dari satu layer digunakan sebagai input untuk layer berikutnya. Jaringan semacam itu disebut jaringan saraf distribusi langsung. Ini berarti bahwa tidak ada loop dalam jaringan - informasi selalu maju, dan tidak pernah memberi umpan balik. Jika kita memiliki loop, kita akan menghadapi situasi di mana input sigmoid akan bergantung pada output. Akan sulit untuk dipahami, dan kami tidak mengizinkan loop seperti itu.

Namun, ada model lain dari NS buatan di mana dimungkinkan untuk menggunakan loop umpan balik. Model-model ini disebut jaringan saraf berulang (RNS). Gagasan dari jaringan-jaringan ini adalah bahwa neuron-neuron mereka diaktifkan untuk periode waktu yang terbatas. Aktivasi ini dapat merangsang neutron lain, yang dapat diaktifkan sedikit kemudian, juga untuk waktu yang terbatas. Ini mengarah pada aktivasi neuron-neuron berikut, dan seiring berjalannya waktu kita mendapatkan kaskade neuron teraktivasi. Loop dalam model seperti itu tidak menimbulkan masalah, karena output neuron mempengaruhi pemasukannya di lain waktu, dan tidak langsung.

RNS tidak berpengaruh seperti NS distribusi langsung, khususnya karena algoritma pelatihan untuk RNS sejauh ini memiliki potensi lebih kecil. Namun, RNS tetap sangat menarik. Dalam semangat kerja, mereka lebih dekat ke otak daripada NS distribusi langsung. Ada kemungkinan bahwa RNS akan dapat memecahkan masalah penting yang dapat diselesaikan dengan kesulitan besar dengan bantuan distribusi langsung NS. Namun, untuk membatasi ruang lingkup penelitian kami, kami akan berkonsentrasi pada NS distribusi langsung yang lebih banyak digunakan.

Jaringan klasifikasi tinta sederhana

Setelah mendefinisikan jaringan saraf, kami akan kembali ke pengenalan tulisan tangan. Tugas mengenali nomor tulisan tangan dapat dibagi menjadi dua subtugas. Pertama, kami ingin menemukan cara untuk membagi gambar yang mengandung banyak digit ke dalam urutan masing-masing gambar, yang masing-masing berisi satu digit. Sebagai contoh, kami ingin membagi gambar



menjadi enam yang terpisah



Kita manusia dapat dengan mudah menyelesaikan masalah segmentasi ini, tetapi sulit bagi program komputer untuk membagi gambar dengan benar. Setelah segmentasi, program perlu mengklasifikasikan setiap digit individu. Jadi, misalnya, kami ingin program kami mengenali angka pertama



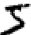
ini 5.

Kami akan berkonsentrasi pada pembuatan program untuk memecahkan masalah kedua, klasifikasi angka individu. Ternyata masalah segmentasi tidak begitu sulit untuk dipecahkan segera setelah kami menemukan cara yang baik untuk mengklasifikasikan digit individu. Ada banyak pendekatan untuk memecahkan masalah segmentasi. Salah satunya adalah mencoba berbagai cara segmentasi gambar menggunakan penggolong dari masing-masing digit, mengevaluasi setiap upaya. Segmentasi uji coba sangat dihargai jika penggolong digit individu yakin dalam klasifikasi semua segmen, dan rendah jika memiliki masalah dalam satu segmen atau lebih. Idenya adalah bahwa jika penggolong memiliki masalah di suatu tempat, ini kemungkinan besar berarti bahwa segmentasi tidak benar. Gagasan ini dan opsi lainnya dapat digunakan untuk solusi yang baik untuk masalah segmentasi. Jadi, alih-alih mengkhawatirkan segmentasi, kami akan berkonsentrasi pada pengembangan NS yang mampu menyelesaikan tugas yang lebih menarik dan kompleks, yaitu, mengenali angka tulisan tangan individu.

Untuk mengenali masing-masing digit, kami akan menggunakan NS dari tiga lapisan:



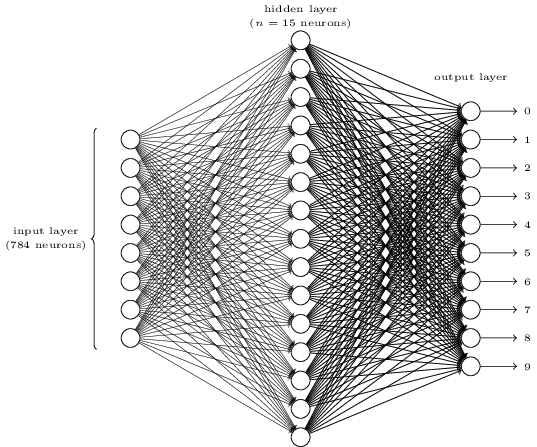
Lapisan jaringan input berisi neuron yang mengkodekan berbagai nilai piksel input. Seperti yang akan ditunjukkan pada bagian selanjutnya, data pelatihan kami akan terdiri dari banyak gambar digit tulisan tangan yang dipindai berukuran 28x28 piksel, sehingga lapisan input berisi 28x28 = 784 neuron. Untuk kesederhanaan, saya tidak menunjukkan sebagian besar 784 neuron dalam diagram. Pixel yang masuk berwarna hitam dan putih, dengan nilai 0,0 mengindikasikan putih, 1,0 mengindikasikan hitam, dan nilai tengah menunjukkan semakin banyak nuansa abu-abu yang semakin gelap.

Lapisan kedua jaringan disembunyikan. Kami menunjukkan jumlah neuron di lapisan ini n, dan kami akan bereksperimen dengan nilai n yang berbeda. Contoh di atas menunjukkan lapisan kecil yang tersembunyi yang hanya mengandung n = 15 neuron.

Ada 10 neuron di lapisan output jaringan. Jika neuron pertama diaktifkan, yaitu, nilai outputnya adalah ≈ 1, ini menunjukkan bahwa jaringan percaya bahwa inputnya adalah 0. Jika neuron kedua diaktifkan, jaringan percaya bahwa inputnya adalah 1. Dan seterusnya. Sebenarnya, kami menomori neuron output dari 0 hingga 9, dan melihat mana di antara mereka yang memiliki nilai aktivasi maksimum. Jika ini, katakanlah, neuron No. 6, maka jaringan kami percaya bahwa inputnya adalah nomor 6. Dan seterusnya.

Anda mungkin bertanya-tanya mengapa kita perlu menggunakan sepuluh neuron. Lagi pula, kami ingin tahu digit mana dari 0 hingga 9 yang sesuai dengan gambar input. Wajar jika hanya menggunakan 4 neuron output, yang masing-masing akan mengambil nilai biner, tergantung pada apakah nilai outputnya lebih dekat ke 0 atau 1. Empat neuron akan cukup, karena 2 ⁴ = 16, lebih dari 10 nilai yang mungkin. Mengapa jaringan kami menggunakan 10 neuron? Apakah ini tidak efektif? Dasar untuk ini adalah empiris; kita dapat mencoba kedua varian jaringan, dan ternyata untuk tugas ini, jaringan dengan 10 neuron output lebih terlatih untuk mengenali angka daripada jaringan dengan 4. Namun, pertanyaannya tetap, mengapa 10 neuron keluaran lebih baik. Apakah ada heuristik yang akan memberitahu kita sebelumnya bahwa 10 neuron output harus digunakan, bukan 4?

Untuk memahami alasannya, penting untuk memikirkan apa yang dilakukan jaringan saraf. Pertama, pertimbangkan opsi dengan 10 neuron output. Kami fokus pada neuron keluaran pertama, yang mencoba memutuskan apakah gambar yang masuk adalah nol. Dia melakukan ini dengan menimbang bukti yang diperoleh dari lapisan tersembunyi. Apa yang dilakukan neuron tersembunyi? Misalkan neuron pertama dalam lapisan tersembunyi menentukan apakah ada sesuatu seperti ini pada gambar:



Ia dapat melakukan ini dengan menetapkan bobot besar ke piksel yang cocok dengan gambar ini, dan bobot kecil untuk sisanya. Dengan cara yang sama, anggaplah bahwa neuron kedua, ketiga dan keempat dalam lapisan tersembunyi mencari apakah ada fragmen yang serupa dalam gambar:



Seperti yang mungkin sudah Anda duga, keempat fragmen ini memberikan gambar 0, yang kita lihat sebelumnya:



Jadi, jika empat neuron tersembunyi diaktifkan, kita dapat menyimpulkan bahwa angkanya adalah 0. Tentu saja, ini bukan satu-satunya bukti bahwa 0 ditampilkan di sana - kita bisa mendapatkan 0 dengan banyak cara lain (dengan sedikit menggeser gambar-gambar ini atau sedikit mengubah mereka). Namun, kita dapat mengatakan dengan pasti bahwa, setidaknya dalam kasus ini, kita dapat menyimpulkan bahwa ada 0 pada input.

Jika kita mengasumsikan bahwa jaringan bekerja seperti ini, kita dapat memberikan penjelasan yang masuk akal mengapa lebih baik menggunakan 10 neuron output daripada 4. Jika kita memiliki 4 neuron output, maka neuron pertama akan mencoba untuk memutuskan apa yang paling signifikan dari digit yang masuk. Dan tidak ada cara mudah untuk mengasosiasikan bit paling signifikan dengan bentuk sederhana yang diberikan di atas. Sulit membayangkan alasan historis mengapa bagian-bagian dari bentuk digit entah bagaimana terkait dengan bit paling signifikan dari output.

Namun, semua hal di atas hanya didukung oleh heuristik. Tidak ada yang mendukung fakta bahwa jaringan tiga lapis harus bekerja seperti yang saya katakan, dan neuron tersembunyi harus menemukan komponen bentuk yang sederhana. Mungkin algoritma pembelajaran yang rumit akan menemukan beberapa bobot yang akan memungkinkan kita untuk menggunakan hanya 4 neuron keluaran. Namun, sebagai heuristik, metode saya berfungsi dengan baik, dan dapat menghemat waktu Anda dalam mengembangkan arsitektur NS yang baik.

Latihan

• , . , . . , 3 , ( ) 0,99, 0,01.

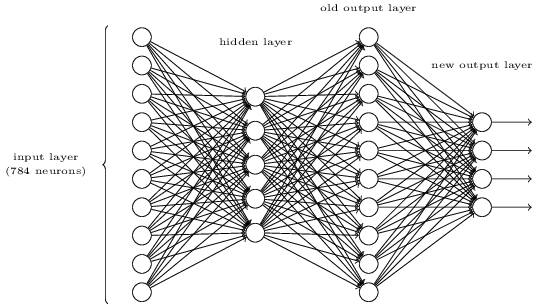Jadi, kami memiliki skema NA - cara belajar mengenali angka? Hal pertama yang kita butuhkan adalah data pelatihan, yang disebut set data pelatihan. Kami akan menggunakan kit MNIST yang berisi puluhan ribu gambar pindaian angka tulisan tangan, dan klasifikasi yang benar. Nama MNIST diterima karena fakta bahwa itu adalah himpunan bagian dari dua set data yang dikumpulkan oleh NIST , Institut Standar dan Teknologi Nasional AS. Berikut adalah beberapa gambar dari MNIST:



Ini adalah angka yang sama yang diberikan pada awal bab sebagai tugas pengenalan. Tentu saja, ketika memeriksa NS, kami akan memintanya untuk mengenali gambar yang salah yang sudah ada di set pelatihan!

Data MNIST terdiri dari dua bagian. Yang pertama berisi 60.000 gambar yang dimaksudkan untuk pelatihan. Ini adalah naskah yang dipindai dari 250 orang, setengah di antaranya adalah karyawan Biro Sensus AS, dan setengah lainnya adalah siswa sekolah menengah. Gambar berwarna hitam dan putih, berukuran 28x28 piksel. Bagian kedua dari dataset MNIST adalah 10.000 gambar untuk menguji jaringan. Ini juga merupakan gambar hitam dan putih 28x28 piksel. Kami akan menggunakan data ini untuk mengevaluasi seberapa baik jaringan telah belajar mengenali angka. Untuk meningkatkan kualitas penilaian, angka-angka ini diambil dari 250 orang lain yang tidak berpartisipasi dalam rekaman set pelatihan (meskipun ini juga karyawan Biro dan siswa sekolah menengah). Ini membantu kami memastikan bahwa sistem kami dapat mengenali tulisan tangan orang-orang yang tidak bertemu selama pelatihan.

Input pelatihan akan dilambangkan dengan x. Akan lebih mudah untuk memperlakukan setiap input gambar x sebagai vektor dengan 28x28 = 784 pengukuran. Setiap nilai di dalam vektor menunjukkan kecerahan satu piksel dalam gambar. Kami akan menunjukkan nilai output sebagai y = y (x), di mana y adalah vektor sepuluh dimensi. Misalnya, jika gambar pelatihan x tertentu berisi 6, maka y (x) = (0,0,0,0,0,0,1,0,0,0,0) ^T akan menjadi vektor yang kita butuhkan. T adalah operasi transpos yang mengubah vektor baris menjadi vektor kolom.

Kami ingin menemukan algoritma yang memungkinkan kami mencari bobot dan offset sedemikian rupa sehingga output jaringan mendekati y (x) untuk semua input pelatihan x. Untuk menghitung perkiraan tujuan ini, kami mendefinisikan fungsi biaya (kadang-kadang disebut fungsi kerugian); dalam buku ini kita akan menggunakan fungsi biaya, tetapi perlu diingat nama lain):

$$

$$C(w, b) = \frac{1}{2n} \sum_x || y(x) – a ||^2 \tag{6}$$

Di sini w menunjukkan seperangkat bobot jaringan, b adalah seperangkat offset, n adalah jumlah data input pelatihan, a adalah vektor data output ketika x adalah input data, dan jumlah melewati semua input pelatihan x. Outputnya, tentu saja, tergantung pada x, w dan b, tetapi untuk kesederhanaan saya tidak menunjuk ketergantungan ini. Notasi || v || berarti panjang vektor v. Kami akan menyebut C fungsi biaya kuadratik; kadang-kadang juga disebut kesalahan standar, atau MSE. Jika Anda mengamati C dengan seksama, Anda dapat melihat bahwa itu tidak negatif, karena semua anggota penjumlahan itu tidak negatif. Selain itu, biaya C (w, b) menjadi kecil, yaitu, C (w, b) ≈ 0, tepatnya ketika y (x) kira-kira sama dengan vektor output a untuk semua data input pelatihan x. Jadi algoritma kami bekerja dengan baik jika kami berhasil menemukan bobot dan offset sehingga C (w, b) ≈ 0. Dan sebaliknya, itu bekerja dengan buruk ketika C (w,b) besar - ini berarti bahwa y (x) tidak cocok dengan output untuk sejumlah besar input. Ternyata tujuan dari algoritma pelatihan adalah untuk meminimalkan biaya C (b, b) sebagai fungsi dari bobot dan offset. Dengan kata lain, kita perlu menemukan satu set bobot dan offset yang meminimalkan nilai biaya. Kami akan melakukan ini menggunakan algoritma yang disebut gradient descent.

Mengapa kita membutuhkan nilai kuadratik? Bukankah kita terutama tertarik pada jumlah gambar yang dikenali dengan benar oleh jaringan? Apakah mungkin untuk memaksimalkan angka ini secara langsung, dan tidak meminimalkan nilai tengah dari nilai kuadratik? Masalahnya adalah bahwa jumlah gambar yang dikenali dengan benar bukanlah fungsi yang mulus dari bobot dan offset jaringan. Sebagian besar, perubahan kecil pada bobot dan offset tidak akan mengubah jumlah gambar yang dikenali dengan benar. Karena itu, sulit untuk memahami bagaimana mengubah bobot dan bias untuk meningkatkan efisiensi. Jika kita menggunakan fungsi biaya yang lancar, akan mudah bagi kita untuk memahami bagaimana membuat perubahan kecil dalam bobot dan offset untuk meningkatkan biaya. Oleh karena itu, pertama-tama kita akan fokus pada nilai kuadrat, dan kemudian kita akan mempelajari keakuratan klasifikasi.

Bahkan mengingat bahwa kami ingin menggunakan fungsi biaya yang lancar, Anda mungkin masih tertarik mengapa kami memilih fungsi kuadrat untuk persamaan (6)? Apakah tidak mungkin untuk memilihnya secara sewenang-wenang? Mungkin jika kita memilih fungsi yang berbeda, kita akan mendapatkan satu set yang sama sekali berbeda untuk meminimalkan bobot dan offset? Sebuah pertanyaan yang masuk akal, dan nanti kita akan kembali memeriksa fungsi biaya dan membuat beberapa perbaikan untuk itu. Namun, fungsi biaya kuadrat berfungsi baik untuk memahami hal-hal dasar dalam mempelajari NS, jadi untuk sekarang kita akan tetap berpegang pada itu.

Untuk meringkas: tujuan kami dalam pelatihan NS adalah untuk menemukan bobot dan offset yang meminimalkan fungsi biaya kuadratik C (b, b). Tugasnya cukup baik, tetapi sejauh ini ia memiliki banyak struktur yang mengganggu - penafsiran w dan b sebagai bobot dan penyeimbang, fungsi σ tersembunyi di latar belakang, pilihan arsitektur jaringan, MNIST, dan sebagainya. Ternyata kita bisa mengerti banyak, mengabaikan sebagian besar struktur ini, dan hanya berkonsentrasi pada aspek minimisasi. Jadi untuk sekarang, kita akan melupakan bentuk khusus fungsi biaya, komunikasi dengan Majelis Nasional, dan sebagainya. Sebaliknya, kita akan membayangkan bahwa kita hanya memiliki fungsi dengan banyak variabel, dan kami ingin menguranginya. Kami akan mengembangkan teknologi yang disebut gradient descent, yang dapat digunakan untuk menyelesaikan masalah tersebut. Dan kemudian kita kembali ke fungsi tertentu,yang kami ingin meminimalkan untuk Majelis Nasional.

Baiklah, katakanlah kita mencoba untuk meminimalkan beberapa fungsi C (v). Ini bisa berupa fungsi apa pun dengan nilai nyata dari banyak variabel v = v ₁ , v ₂ , ... Perhatikan bahwa saya mengganti notasi w dan b dengan v untuk menunjukkan bahwa itu bisa berupa fungsi apa pun - kita tidak lagi terobsesi dengan HC. Sangat berguna untuk membayangkan bahwa fungsi C hanya memiliki dua variabel - v ₁ dan v ₂ :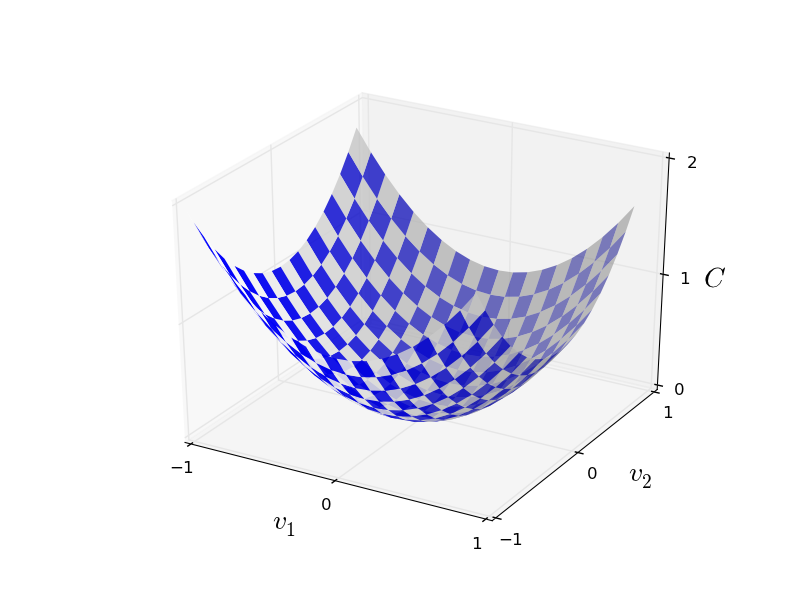



Kami ingin menemukan di mana C mencapai minimum global. Tentu saja, dengan fungsi yang digambarkan di atas, kita dapat mempelajari grafik dan menemukan minimum. Dalam hal ini, saya mungkin telah memberi Anda fungsi yang terlalu sederhana! Dalam kasus umum, C dapat menjadi fungsi kompleks dari banyak variabel, dan biasanya tidak mungkin untuk hanya melihat grafik dan menemukan minimum.

Salah satu cara untuk memecahkan masalah adalah dengan menggunakan aljabar untuk menemukan minimum secara analitis. Kita dapat menghitung turunan dan mencoba menggunakannya untuk menemukan ekstrem. Jika kita beruntung, ini akan berfungsi ketika C adalah fungsi dari satu atau dua variabel. Tetapi dengan sejumlah besar variabel, ini berubah menjadi mimpi buruk. Dan untuk NS kita sering membutuhkan lebih banyak variabel - untuk NS terbesar, fungsi biaya dengan cara yang kompleks tergantung pada miliaran bobot dan perpindahan. Menggunakan aljabar untuk meminimalkan fungsi-fungsi ini akan gagal!

(Setelah menyatakan bahwa akan lebih nyaman bagi kita untuk menganggap C sebagai fungsi dari dua variabel, saya mengatakan dua kali dalam dua paragraf “ya, tetapi bagaimana jika itu adalah fungsi dari variabel yang jauh lebih besar?” Saya minta maaf. dua variabel, hanya saja kadang-kadang gambar ini berantakan, itulah sebabnya dua paragraf sebelumnya diperlukan. ZYA.)

Oke, itu artinya aljabar tidak akan bekerja. Untungnya, ada analogi yang bagus yang menawarkan algoritma yang berfungsi dengan baik. Kami membayangkan fungsi kami seperti lembah. Dengan jadwal terbaru, tidak akan terlalu sulit untuk dilakukan. Dan kita membayangkan sebuah bola menggelinding di sepanjang lereng lembah. Pengalaman kami memberi tahu kami bahwa bola pada akhirnya akan meluncur ke bagian paling bawah. Mungkin kita bisa menggunakan ide ini untuk menemukan fungsi minimum? Kami secara acak memilih titik awal untuk bola imajiner, dan kemudian mensimulasikan pergerakan bola, seolah-olah itu bergulir ke dasar lembah. Kita dapat menggunakan simulasi ini hanya dengan menghitung turunan (dan, mungkin, turunan kedua) dari C - mereka akan memberi tahu kita segala sesuatu tentang bentuk lokal lembah, dan karenanya tentang bagaimana bola kita akan bergulir.

Berdasarkan apa yang Anda tulis, Anda mungkin berpikir bahwa kami akan menuliskan persamaan gerak Newton untuk bola, mempertimbangkan efek gesekan dan gravitasi, dan sebagainya. Faktanya, kita tidak akan begitu dekat dengan analogi ini dengan bola - kita sedang mengembangkan algoritma untuk meminimalkan C, dan bukan simulasi yang tepat dari hukum fisika! Analogi ini harus merangsang imajinasi kita, dan tidak membatasi pemikiran kita. Jadi alih-alih menyelam ke detail fisika yang kompleks, mari kita ajukan pertanyaan: jika kita ditunjuk sebagai dewa untuk satu hari, dan kita akan membuat hukum fisika kita sendiri, memberi tahu bola cara menggulung hukum mana atau hukum gerak yang akan kita pilih, sehingga bola selalu bergulir ke atas bawah lembah?

Untuk mengklarifikasi masalah ini, kami akan memikirkan tentang apa yang terjadi jika kami memindahkan bola sedikit 1v ₁ ke arah v ₁, dan jarak kecil Δv ₂ ke arah v ₂ . Aljabar memberi tahu kita bahwa C berubah sebagai berikut:

$$

$$\Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2 \tag{7}$$

Kami akan menemukan cara untuk memilih Δv ₁ dan Δv ₂ sehingga ΔC kurang dari nol; yaitu, kami akan memilih mereka sehingga bola bergulir ke bawah. Untuk memahami bagaimana melakukan ini, penting untuk mendefinisikan asv sebagai vektor perubahan, yaitu, Δv ≡ (Δv ₁ , 2v ₂ ) ^T , di mana T adalah operasi transpos yang mengubah vektor baris menjadi vektor kolom. Kami juga mendefinisikan vektor gradien C sebagai derivatif parsial (∂S / ∂v ₁ , ∂S / ∂v ₂ ) ^T . Kami menunjukkan vektor gradien oleh ∇:

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2})^T \tag{8}$$

Segera kami akan menulis ulang perubahan ΔC hingga Δv dan gradien ∇C. Sementara itu, saya ingin mengklarifikasi sesuatu, karena itu orang sering bergantung pada gradien. Ketika mereka pertama kali bertemu dengan ∇C, orang kadang-kadang tidak mengerti bagaimana mereka harus memahami simbol ∇. Apa artinya secara khusus? Bahkan, Anda dapat dengan aman mempertimbangkan ∇C sebagai objek matematika tunggal - vektor yang telah ditentukan sebelumnya - yang hanya ditulis menggunakan dua karakter. Dari sudut pandang ini, ∇ seperti mengibarkan bendera yang menginformasikan bahwa "∇C adalah vektor gradien." Ada beberapa sudut pandang yang lebih maju dari mana ∇ dapat dianggap sebagai entitas matematika independen (misalnya, sebagai operator diferensiasi), tetapi kami tidak membutuhkannya.

Dengan definisi seperti itu, ekspresi (7) dapat ditulis ulang sebagai:

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{9}$$

Persamaan ini membantu menjelaskan mengapa ∇C disebut vektor gradien: ia menghubungkan perubahan v dengan perubahan C, sama seperti yang diharapkan dari entitas yang disebut gradien. [eng. gradient - deviasi / kira-kira. terjemahan.] Namun, lebih menarik bahwa persamaan ini memungkinkan kita untuk melihat bagaimana memilih Δv sehingga ΔC negatif. Katakanlah kita memilih

$$

$$\Delta v = - \eta \nabla C \tag{10}$$

di mana η adalah parameter positif kecil (kecepatan belajar). Kemudian persamaan (9) memberi tahu kita bahwa ΔC ≈ - η ∇C ⋅ ∇C = - η || ∇C || ² . Sejak || ∇C || ² ≥ 0, ini memastikan bahwa ΔC ≤ 0, yaitu, C akan berkurang sepanjang waktu jika kita mengubah v, sebagaimana ditentukan dalam (10) (tentu saja, sebagai bagian dari perkiraan dari persamaan (9)). Dan inilah yang kita butuhkan! Oleh karena itu, kita mengambil persamaan (10) untuk menentukan "hukum gerak" bola dalam algoritma gradient descent kami. Artinya, kita akan menggunakan persamaan (10) untuk menghitung nilai Δv, dan kemudian kita akan memindahkan bola ke nilai ini:

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{11}$$

Kemudian kami kembali menerapkan aturan ini untuk langkah selanjutnya. Melanjutkan pengulangan, kami akan menurunkan C hingga, semoga, kami mencapai minimum global.

Kesimpulannya, gradient descent bekerja melalui perhitungan sekuensial dari gradien ∇ C, dan perpindahan selanjutnya dalam arah yang berlawanan, yang mengarah pada “jatuh” di sepanjang lereng lembah. Ini dapat divisualisasikan sebagai berikut: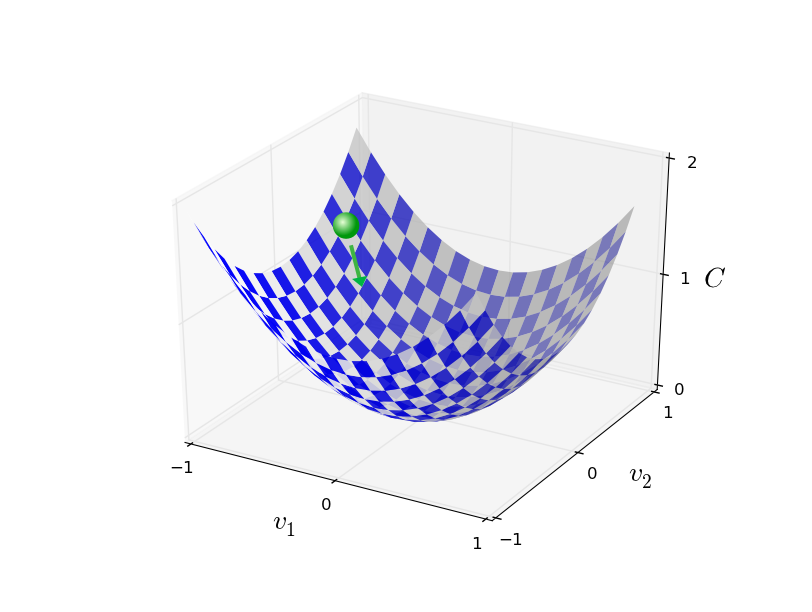



Perhatikan bahwa dengan aturan ini, gradient descent tidak mereproduksi gerak fisik nyata. Dalam kehidupan nyata, bola memiliki dorongan yang memungkinkan bola bergulir melewati lereng, atau bahkan menggulung selama beberapa waktu. Hanya setelah pekerjaan gaya gesekan, bola dijamin akan bergulir ke bawah lembah. Aturan seleksi kami Δv hanya mengatakan "turun". Aturan yang cukup bagus untuk menemukan minimum!

Agar gradient descent berfungsi dengan benar, kita perlu memilih nilai kecepatan pembelajaran yang cukup kecil η sehingga persamaan (9) adalah perkiraan yang baik. Kalau tidak, mungkin akan menghasilkan ΔC> 0 - tidak ada yang baik! Pada saat yang sama, η tidak perlu terlalu kecil, karena perubahan Δv akan menjadi kecil, dan algoritme akan bekerja terlalu lambat. Dalam prakteknya, η berubah sehingga persamaan (9) memberikan perkiraan yang baik, dan algoritma tidak bekerja terlalu lambat. Nanti kita akan lihat cara kerjanya.

Saya menjelaskan gradient descent ketika fungsi C hanya bergantung pada dua variabel. Tetapi semuanya bekerja dengan cara yang sama jika C adalah fungsi dari banyak variabel. Misalkan dia memiliki variabel m, v ₁ , ..., v _m. Maka perubahan ΔC yang disebabkan oleh perubahan kecil dalam Δv = (Δv ₁ , ..., Δv _m ) ^T akan menjadi

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{12}$$

di mana gradien ∇C adalah vektor

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1},…, \frac{\partial C}{\partial v_m})^T \tag{13}$$

Seperti halnya dua variabel, kita dapat memilih

$$

$$\Delta v = - \eta \nabla C \tag{14}$$

dan memastikan bahwa perkiraan kami (12) untuk ΔC negatif. Ini memberi kita cara untuk menjalankan gradien ke minimum, bahkan ketika C adalah fungsi dari banyak variabel, menerapkan aturan pembaruan berulang-ulang.

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{15}$$

Aturan pembaruan ini dapat dianggap sebagai algoritma penurunan gradien pendefinisian. Ini memberi kita metode berulang kali mengubah posisi v dalam mencari minimum fungsi C. Aturan ini tidak selalu berfungsi - beberapa hal bisa salah, mencegah gradien keturunan menemukan minimum global C - kita akan kembali ke titik ini dalam bab-bab berikut. Namun dalam praktiknya, gradient descent sering bekerja dengan sangat baik, dan kita akan melihat bahwa di Majelis Nasional ini adalah cara yang efektif untuk meminimalkan fungsi biaya, dan karenanya, melatih jaringan.

Dalam arti tertentu, gradient descent dapat dianggap sebagai strategi pencarian minimum yang optimal. Misalkan kita sedang mencoba memindahkan tov ke posisi untuk meminimalkan C. Ini sama dengan meminimalkan ΔC ≈ ∇C ⋅ Δv. Kami akan membatasi ukuran langkah sehingga || Δv || = ε untuk beberapa konstanta kecil ε> 0. Dengan kata lain, kami ingin memindahkan jarak kecil dari ukuran tetap, dan mencoba menemukan arah gerakan yang mengurangi C sebanyak mungkin. Dapat dibuktikan bahwa pilihan minimv meminimalkan ∇C ⋅ Δv adalah Δv = -η∇C, di mana η = ε / || ∇C || ditentukan oleh batasan || Δv || = ε. Jadi gradient descent dapat dianggap sebagai cara untuk mengambil langkah-langkah kecil ke arah yang paling banyak menurunkan C.

Latihan

• . : — , , , .
• , , . , ? ?

Orang-orang telah mempelajari banyak pilihan untuk gradient descent, termasuk yang lebih akurat mereproduksi bola fisik nyata. Opsi semacam itu memiliki kelebihan, tetapi juga kelemahan besar: kebutuhan untuk menghitung turunan parsial kedua C, yang dapat menghabiskan banyak sumber daya. Untuk memahami hal ini, anggaplah kita perlu menghitung semua turunan parsial kedua ∂ ² C / ∂v _j ∂v _k . Jika variabel _{vj adalah} juta, maka kita perlu menghitung sekitar satu triliun (satu juta kuadrat) dari turunan parsial kedua (sebenarnya, setengah triliun, karena ∂ ² C / ∂v _j ∂v _k = ∂ ² C / ∂v _k ∂v _j. Tetapi Anda menangkap esensinya). Ini akan membutuhkan banyak sumber daya komputasi. Ada trik untuk menghindari ini, dan mencari alternatif untuk gradient descent adalah bidang penelitian aktif. Namun, dalam buku ini kita akan menggunakan gradient descent dan variannya sebagai pendekatan utama untuk mempelajari NS.

Bagaimana kita menerapkan gradient descent pada pembelajaran NA? Kita perlu menggunakannya untuk mencari bobot w _k dan offset b _l yang meminimalkan persamaan biaya (6). Mari kita menulis ulang aturan pembaruan gradient descent dengan mengganti variabel _vj dengan bobot dan offset. Dengan kata lain, sekarang kami "posisi" adalah komponen dari w _k dan b _l , sedangkan vektor gradient ∇C telah komponen ∂C / ∂w sesuai_k dan ∂C / ∂b _l . Setelah menulis aturan pembaruan kami dengan komponen baru, kami mendapatkan:

$$

$$w_k \rightarrow w'_k = w_k - \eta \frac{\partial C}{\partial w_k} \tag{16}$$

$$

$$b_l \rightarrow b'_l = b_l - \eta \frac{\partial C}{\partial b_l} \tag{17}$$

Dengan menerapkan kembali aturan pembaruan ini, kita dapat "meluncur turun" dan, dengan sedikit keberuntungan, menemukan fungsi biaya minimum. Dengan kata lain, aturan ini dapat digunakan untuk melatih Majelis Nasional.

Ada beberapa kendala untuk menerapkan aturan gradient descent. Kami akan mempelajarinya secara lebih rinci dalam bab-bab berikut. Tetapi untuk sekarang, saya hanya ingin menyebutkan satu masalah. Untuk memahaminya, mari kita kembali ke nilai kuadrat dalam persamaan (6). Perhatikan bahwa fungsi biaya ini terlihat seperti C = 1 / n _x C _x , yaitu biaya rata-rata C _x ≡ (|| y (x) −a || ² ) / 2 untuk contoh pelatihan individual. Dalam praktiknya, untuk menghitung gradien ∇C, kita perlu menghitung gradien ∇C _x secara terpisah untuk setiap input pelatihan x, dan kemudian rata-rata, ∇C = 1 / n _{x x} ∇C _x . Sayangnya, ketika jumlah input akan sangat besar, itu akan memakan waktu yang sangat lama, dan pelatihan seperti itu akan lambat.

Untuk mempercepat pembelajaran, Anda dapat menggunakan keturunan gradien stokastik. Idenya adalah untuk kira-kira menghitung gradien ∇C dengan menghitung ∇C _x untuk sampel acak kecil dari input pelatihan. Dengan menghitung rata-rata, kita dapat dengan cepat mendapatkan estimasi yang baik dari gradien sebenarnya ∇C, dan ini membantu mempercepat gradient descent, dan karenanya melatih.

Merumuskan lebih tepat, penurunan gradien stokastik bekerja melalui pengambilan sampel acak dari sejumlah kecil data input pelatihan. Kami akan memanggil data acak ini X ₁ , X ₂ , .., X _m , dan menyebutnya paket mini. Jika ukuran sampel m cukup besar, nilai rata-rata ∇C _{X j} akan cukup dekat dengan rata-rata semua ∇Cx, yaitu.

$$

$$\ frac {\ sum ^ m_ {j = 1} \ nabla C_ {X_j}} {m} \ approx \ frac {\ sum_x \ nabla C_x} {n} = \ nabla C \ tag {18}$$

di mana jumlah kedua melewati seluruh set data pelatihan. Dengan menukar bagian, kita dapatkan

$$

$$\ nabla C \ approx \ frac {1} {m} \ jumlah ^ m_ {j = 1} \ nabla C_ {X_j} \ tag {19}$$

yang mengonfirmasi bahwa kita dapat memperkirakan gradien keseluruhan dengan menghitung gradien untuk minipack yang dipilih secara acak.

Untuk mengaitkan ini langsung dengan pelatihan NS, mari kita asumsikan bahwa _wk dan b _l menunjukkan bobot dan perpindahan NS kita. Kemudian keturunan gradien stokastik memilih paket mini acak dari data input, dan belajar dari mereka

$$

$$w_k \ rightarrow w'_k = w_k - \ frac {\ eta} {m} \ sum_j \ frac {\ partial C_ {X_j}} {\ partial w_k} \ tag {20}$$

$$

$$b_l \ rightarrow b'_l = b_l - \ frac {\ eta} {m} \ sum_j \ frac {\ partial C_ {X_j}} {\ partial b_l} \ tag {21}$$

di mana penjumlahan atas semua contoh pelatihan X _j dalam paket mini saat ini. Kemudian kami memilih satu paket mini acak dan mempelajarinya. Dan seterusnya, sampai kita menghabiskan semua data pelatihan, yang disebut akhir dari era pelatihan. Pada saat ini, kita memulai era baru pembelajaran.

Ngomong-ngomong, perlu dicatat bahwa perjanjian mengenai penskalaan fungsi biaya dan memperbarui bobot dan offset berbeda dalam paket mini. Dalam persamaan (6), kami meningkatkan fungsi biaya 1 / n kali. Kadang-kadang orang menghilangkan 1 / n dengan menambahkan biaya contoh pelatihan individu, bukannya menghitung rata-rata. Ini berguna ketika jumlah total contoh pelatihan tidak diketahui sebelumnya. Ini bisa terjadi, misalnya, ketika data tambahan muncul secara real time. Dengan cara yang sama, aturan pembaruan paket mini (20) dan (21) kadang-kadang menghilangkan anggota 1 / m di depan jumlah. Secara konseptual, ini tidak mempengaruhi apa pun, karena ini setara dengan perubahan dalam kecepatan belajar η. Namun, perlu diperhatikan ketika membandingkan berbagai karya.

Keturunan gradien stokastik dapat dianggap sebagai pemungutan suara politik: jauh lebih mudah untuk mengambil sampel dalam bentuk paket-mini daripada menerapkan gradient descent ke sampel penuh - sama seperti jajak pendapat di pintu keluar dari situs lebih mudah untuk dilakukan daripada pemilihan penuh. Misalnya, jika set pelatihan kami memiliki ukuran n = 60.000, seperti MNIST, dan kami membuat sampel paket mini ukuran m = 10, maka kami akan mempercepat estimasi gradien sebanyak 6000 kali! Tentu saja, estimasi tidak akan ideal - akan ada fluktuasi statistik di dalamnya - tetapi itu tidak perlu ideal: kita hanya perlu bergerak ke arah yang mengurangi C, yang berarti bahwa kita tidak perlu menghitung gradien secara akurat. Dalam praktiknya, penurunan gradien stokastik adalah teknik pengajaran yang umum dan kuat untuk Majelis Nasional, dan basis dari sebagian besar teknologi pengajaran yang akan kami kembangkan sebagai bagian dari buku ini.

Latihan

• Versi ekstrim dari gradient descent menggunakan ukuran paket-mini sama dengan 1. Yaitu, dengan input x kami memperbarui bobot dan offset kami sesuai dengan aturan wk → w ′ _k = w _k - η xC _x / ∂w _k dan b _l → b ′ _L = b _l - η ∂C _x / ∂b _l . Kemudian kami memilih contoh input pelatihan lainnya dan memperbarui bobot dan offset. Dan sebagainya. Prosedur ini dikenal sebagai pembelajaran online, atau tambahan. Dalam pembelajaran online, studi NS berdasarkan pada satu salinan pelatihan dari data input pada suatu waktu (seperti orang). Apa kelebihan dan kekurangan dari pembelajaran online dibandingkan dengan stochastic gradient descent dengan ukuran paket mini 20?

Biarkan saya mengakhiri bagian ini dengan diskusi tentang suatu topik yang kadang-kadang mengganggu orang yang pertama kali mengalami penurunan gradien. Di NS, nilai C adalah fungsi dari banyak variabel - semua bobot dan offset - dan dalam arti tertentu, menentukan permukaan dalam ruang yang sangat multidimensi. Orang-orang mulai berpikir: "Saya harus memvisualisasikan semua dimensi tambahan ini." Dan mereka mulai khawatir: "Saya tidak bisa menavigasi dalam empat dimensi, belum lagi lima (atau lima juta)." Apakah mereka memiliki kualitas istimewa yang dimiliki oleh supermathemik “asli”? Tentu saja tidak. Bahkan matematikawan profesional tidak dapat memvisualisasikan ruang empat dimensi dengan cukup baik - jika sama sekali. Mereka melakukan trik, mengembangkan cara lain untuk mewakili apa yang terjadi. Kami melakukan hal itu: kami menggunakan representasi aljabar (bukan visual) dari ΔC untuk memahami cara bergerak sehingga C berkurang. Orang-orang yang berprestasi baik dengan sejumlah besar dimensi memiliki perpustakaan besar teknik yang sama di benak mereka; trik aljabar kita hanyalah satu contoh. Teknik-teknik ini mungkin tidak sesederhana yang biasa kita lakukan ketika memvisualisasikan tiga dimensi, tetapi ketika Anda membuat perpustakaan teknik yang serupa, Anda mulai berpikir dengan baik dalam dimensi yang lebih tinggi. Saya tidak akan membahas secara terperinci, tetapi jika Anda tertarik, Anda mungkin menyukai diskusi tentang beberapa teknik ini oleh ahli matematika profesional yang terbiasa berpikir dalam dimensi yang lebih tinggi. Meskipun beberapa teknik yang dibahas cukup kompleks, sebagian besar jawaban terbaik bersifat intuitif dan dapat diakses oleh semua orang.

Menerapkan jaringan untuk mengklasifikasikan angka

Ok, sekarang mari kita menulis sebuah program yang belajar mengenali angka tulisan tangan menggunakan stochastic gradient descent dan data pelatihan dari MNIST. Kami akan melakukan ini dengan program pendek dalam python 2.7 yang hanya terdiri dari 74 baris! Hal pertama yang kita butuhkan adalah mengunduh data MNIST. Jika Anda menggunakan git, maka Anda bisa mendapatkannya dengan mengkloning repositori buku ini:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git

Jika tidak, unduh kode dari tautan .

Omong-omong, ketika saya menyebutkan data MNIST sebelumnya, saya mengatakan bahwa mereka dibagi menjadi 60.000 gambar pelatihan dan 10.000 gambar uji. Ini adalah deskripsi resmi dari MNIST. Kami akan memecah data sedikit berbeda. Kami akan membiarkan gambar verifikasi tidak berubah, tetapi kami akan membagi set pelatihan menjadi dua bagian: 50.000 gambar, yang akan kami gunakan untuk melatih Majelis Nasional, dan masing-masing 10.000 gambar untuk konfirmasi tambahan. Meskipun kami tidak akan menggunakannya, tetapi nanti mereka akan berguna bagi kami ketika kami akan memahami konfigurasi beberapa parameter hiper NS - kecepatan belajar, dll. - yang tidak dipilih langsung oleh algoritma kami. Meskipun data yang menguatkan bukan bagian dari spesifikasi MNIST asli, banyak yang menggunakan MNIST dengan cara ini, dan di bidang HC penggunaan data yang menguatkan adalah umum. Sekarang, berbicara tentang "data pelatihan MNIST," maksud saya adalah 50.000 karitnoks kami, bukan 60.000 yang asli.

Selain data MNIST, kita juga membutuhkan pustaka python bernama Numpy untuk perhitungan aljabar linier cepat. Jika Anda tidak memilikinya, Anda dapat mengambilnya dari tautan .

Sebelum memberi Anda seluruh program, izinkan saya menjelaskan fitur utama kode untuk NS. Tempat sentral ditempati oleh kelas Jaringan, yang kami gunakan untuk mewakili Majelis Nasional. Berikut adalah kode inisialisasi untuk objek Jaringan:

 class Network(object): def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] 

Array ukuran berisi jumlah neuron di lapisan yang sesuai. Jadi, jika kita ingin membuat objek Jaringan dengan dua neuron di lapisan pertama, tiga neuron di lapisan kedua, dan satu neuron di lapisan ketiga, maka kita akan menulis seperti ini:

 net = Network([2, 3, 1]) 

Offset dan bobot dalam objek Jaringan diinisialisasi secara acak menggunakan fungsi numpy np.random.randn, yang menghasilkan distribusi Gaussian dengan ekspektasi matematis dari 0 dan standar deviasi 1. Inisialisasi acak ini memberikan algoritma penurunan gradien stochastic kami sebagai titik awal. Dalam bab-bab berikut, kami akan menemukan cara terbaik untuk menginisialisasi bobot dan offset, tetapi untuk saat ini cukup. Perhatikan bahwa kode inisialisasi jaringan mengasumsikan bahwa lapisan pertama neuron akan menjadi input, dan tidak memberikan mereka bias, karena mereka hanya digunakan untuk menghitung output.

Perhatikan juga bahwa offset dan bobot disimpan sebagai array matriks Numpy. Sebagai contoh, net.weights [1] adalah matriks Numpy yang menyimpan bobot yang menghubungkan lapisan neuron kedua dan ketiga (ini bukan lapisan pertama dan kedua, karena dalam python penomoran elemen-elemen array berasal dari awal). Karena akan memakan waktu terlalu lama untuk menulis net.weights [1], kami menyatakan matriks ini sebagai w. Ini adalah suatu matriks yang _wjk adalah bobot hubungan antara neuron k di lapisan kedua dan neuron ke-j di lapisan ketiga. Urutan indeks j dan k seperti itu mungkin tampak aneh - bukankah lebih logis untuk menukar mereka? Tetapi keuntungan besar dari rekaman tersebut adalah bahwa vektor aktivasi dari lapisan ketiga neuron diperoleh:

$$

$$a '= \ sigma (wa + b) \ tag {22}$$

Mari kita lihat persamaan yang cukup kaya ini. a adalah vektor aktivasi lapisan kedua neuron. Untuk mendapatkan ', kita mengalikan a dengan matriks bobot w, dan menambahkan vektor perpindahan b. Kemudian kita menerapkan elemen σ sigmoid demi elemen ke setiap elemen vektor wa + b (ini disebut vektorisasi fungsi σ). Mudah untuk memverifikasi bahwa persamaan (22) memberikan hasil yang sama dengan aturan (4) untuk menghitung neuron sigmoid.

Latihan

• Tulis persamaan (22) dalam bentuk komponen, dan pastikan itu memberikan hasil yang sama dengan aturan (4) untuk menghitung neuron sigmoid.

Dengan semua ini dalam pikiran, mudah untuk menulis kode yang menghitung output dari objek Network. Kita mulai dengan mendefinisikan sigmoid:

 def sigmoid(z): return 1.0/(1.0+np.exp(-z)) 

Perhatikan bahwa ketika parameter z adalah vektor atau array Numpy, Numpy akan secara otomatis menerapkan elemen sigmoid, yaitu dalam bentuk vektor.

Tambahkan metode propagasi langsung ke kelas Jaringan, yang mengambil dari jaringan sebagai input dan mengembalikan output yang sesuai. Diasumsikan bahwa parameter a adalah (n, 1) Numpy ndarray, bukan vektor (n,). Di sini n adalah jumlah neuron input. Jika Anda mencoba menggunakan vektor (n,), Anda akan mendapatkan hasil yang aneh.

Metode ini hanya menerapkan persamaan (22) untuk setiap lapisan:

  def feedforward(self, a): """       "a"""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a 

Tentu saja, pada dasarnya kita dari objek Network membutuhkannya untuk dipelajari. Untuk melakukan ini, kami akan memberi mereka metode SGD, yang mengimplementasikan penurunan gradien stokastik. Ini kodenya. Di beberapa tempat itu agak misterius, tetapi di bawah ini kami akan menganalisisnya lebih detail.

  def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) 

training_data adalah daftar tupel "(x, y)" yang mewakili input pelatihan dan output yang diinginkan. Variabel epochs dan mini_batch_size adalah jumlah zaman untuk dipelajari dan ukuran paket mini yang digunakan. eta - kecepatan belajar, η. Jika test_data disetel, maka jaringan akan dievaluasi terhadap data verifikasi setelah setiap era, dan kemajuan saat ini akan ditampilkan. Ini berguna untuk melacak kemajuan, tetapi secara signifikan memperlambat pekerjaan.

Kode kerjanya seperti ini. Di setiap era, ia mulai dengan secara tidak sengaja mencampurkan data pelatihan, dan kemudian memecahnya menjadi paket mini dengan ukuran yang tepat. Ini adalah cara mudah untuk membuat sampel data pelatihan. Kemudian untuk setiap mini_batch kami menerapkan satu langkah gradient descent. Ini dilakukan oleh kode self.update_mini_batch (mini_batch, eta), yang memperbarui bobot dan offset jaringan menurut satu iterasi dari penurunan gradien menggunakan hanya data pelatihan di mini_batch. Berikut adalah kode untuk metode update_mini_batch:

  def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] 

Sebagian besar pekerjaan dilakukan oleh garis.

  delta_nabla_b, delta_nabla_w = self.backprop(x, y) 

Ini memanggil algoritma backpropagation - cara cepat untuk menghitung gradien dari fungsi biaya. Jadi, update_mini_batch cukup menghitung gradien ini untuk setiap contoh pelatihan dari mini_batch, dan kemudian memperbarui self.weights dan self.biases.

Sejauh ini, saya tidak akan menunjukkan kode untuk self.backprop. Kita akan belajar tentang backpropagation di bab selanjutnya, dan akan ada kode self.backprop. Untuk saat ini, anggaplah berperilaku seperti yang dinyatakan, mengembalikan gradien yang sesuai untuk biaya yang terkait dengan contoh pelatihan x.

Mari kita lihat keseluruhan program, termasuk komentar penjelasan. Dengan pengecualian fungsi self.backprop, program berbicara sendiri - pekerjaan utama dilakukan oleh self.SGD dan self.update_mini_batch. Metode self.backprop menggunakan beberapa fungsi tambahan untuk menghitung gradien, yaitu sigmoid_prime, yang menghitung turunan dari sigmoid, dan self.cost_derivative, yang tidak akan saya jelaskan di sini. Anda bisa mendapatkan ide tentang mereka dengan melihat kode dan komentar. Dalam bab selanjutnya kita akan membahasnya secara lebih rinci. Ingatlah bahwa meskipun programnya tampak panjang, sebagian besar kode adalah komentar yang membuatnya lebih mudah untuk dipahami. Bahkan, program itu sendiri hanya terdiri dari 74 kode non-baris - tidak kosong dan tidak komentar. Semua kode tersedia di GitHub .

 """ network.py ~~~~~~~~~~           .      .     ,    .   ,       . """ ####  #   import random #   import numpy as np class Network(object): def __init__(self, sizes): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].               0    1. ,      ,       ,        . """ self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] def feedforward(self, a): """   ,  ``a`` -  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) #   delta = self.cost_derivative(activations[-1], y) * \ sigmoid_prime(zs[-1]) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """ l      ,      . l = 1    , l = 2 – ,   .    ,   python      .""" for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def evaluate(self, test_data): """    ,      .    –          .""" test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data] return sum(int(x == y) for (x, y) in test_results) def cost_derivative(self, output_activations, y): """    ( C_x /  a)   .""" return (output_activations-y) ####   def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

Seberapa baik program mengenali angka tulisan tangan? Mari kita mulai dengan memuat data MNIST. Kami akan melakukan ini menggunakan program pembantu kecil mnist_loader.py, yang akan saya jelaskan di bawah ini. Jalankan perintah berikut di shell python:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Ini, tentu saja, dapat dilakukan dalam program terpisah, tetapi jika Anda bekerja secara paralel dengan sebuah buku, itu akan lebih mudah.

Setelah mengunduh data MNIST, atur jaringan 30 neuron tersembunyi. Kami akan melakukan ini setelah mengimpor program yang dijelaskan di atas, yang disebut jaringan:

 >>> import network >>> net = network.Network([784, 30, 10]) 

Akhirnya, kami menggunakan keturunan gradien stokastik untuk pelatihan data pelatihan selama 30 era, dengan ukuran paket mini 10, dan kecepatan belajar η = 3.0:

 >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Jika Anda mengeksekusi kode secara paralel dengan membaca buku, perlu diketahui bahwa akan membutuhkan beberapa menit untuk mengeksekusi. Saya sarankan Anda memulai semuanya, terus membaca, dan secara berkala memeriksa apa yang dihasilkan oleh program. Jika Anda terburu-buru, Anda dapat mengurangi jumlah era dengan mengurangi jumlah neuron tersembunyi, atau hanya menggunakan sebagian data pelatihan. Kode kerja terakhir akan bekerja lebih cepat: skrip python ini dirancang untuk membuat Anda memahami cara kerja jaringan, dan tidak berkinerja tinggi! Dan, tentu saja, setelah pelatihan, jaringan dapat bekerja dengan sangat cepat di hampir semua platform komputasi. Misalnya, ketika kami mengajarkan jaringan pilihan bobot dan offset yang baik, jaringan dapat dengan mudah dipindahkan untuk berfungsi pada JavaScript di peramban web, atau sebagai aplikasi asli pada perangkat seluler. Dalam kasus apa pun, kesimpulan yang kira-kira sama dibuat oleh program yang melatih jaringan saraf. Dia menulis jumlah gambar uji yang diakui dengan benar setelah setiap era pelatihan. Seperti yang Anda lihat, bahkan setelah satu era, ia mencapai akurasi 9.129 dari 10.000, dan jumlah ini terus bertambah:

Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000

Ternyata jaringan terlatih memberikan persentase klasifikasi yang benar sekitar 95 - 95,42% maksimal! Upaya pertama yang cukup menjanjikan. Saya memperingatkan Anda bahwa kode Anda tidak harus menghasilkan hasil yang persis sama, karena kami menginisialisasi jaringan dengan bobot dan offset acak. Untuk bab ini, saya telah memilih yang terbaik dari tiga upaya.

Mari kita mulai kembali percobaan dengan mengubah jumlah neuron tersembunyi menjadi 100. Seperti sebelumnya, jika Anda menjalankan kode pada saat yang sama dengan membaca, perlu diketahui bahwa itu membutuhkan banyak waktu (pada mesin saya, setiap era membutuhkan beberapa puluh detik), jadi lebih baik membaca secara paralel dengan eksekusi kode.

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Secara alami, ini meningkatkan hasilnya menjadi 96,59%. Setidaknya dalam kasus ini, menggunakan lebih banyak neuron tersembunyi membantu mendapatkan hasil yang lebih baik.

Umpan balik dari pembaca menunjukkan bahwa hasil percobaan ini sangat bervariasi, dan beberapa hasil pembelajaran jauh lebih buruk. Menggunakan teknik dari Bab 3 untuk secara serius mengurangi keragaman efisiensi kerja dari satu proses ke yang lain.

Tentu saja, untuk mencapai akurasi seperti itu, saya harus memilih sejumlah era untuk belajar, ukuran paket mini dan kecepatan belajar η. Seperti yang saya sebutkan di atas, mereka disebut hyperparameters dari Majelis Nasional kami - untuk membedakan mereka dari parameter sederhana (bobot dan offset) yang disesuaikan oleh algoritma selama pelatihan. Jika kita memilih hyperparameters dengan buruk, kita akan mendapatkan hasil yang buruk. Misalkan, misalnya, bahwa kami telah memilih tingkat pembelajaran η = 0,001:

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data) 

Hasilnya jauh lebih mengesankan:

Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000

Namun, Anda dapat melihat bahwa efisiensi jaringan perlahan-lahan tumbuh seiring waktu. Ini menunjukkan bahwa Anda dapat mencoba meningkatkan kecepatan belajar, misalnya, menjadi 0,01. Dalam hal ini, hasilnya akan lebih baik, yang menunjukkan kebutuhan untuk lebih meningkatkan kecepatan (jika perubahan memperbaiki situasi, ubah lebih lanjut!). Jika Anda melakukan ini beberapa kali, kami akhirnya akan tiba di η = 1.0 (dan kadang-kadang bahkan 3.0), yang dekat dengan eksperimen kami sebelumnya. Jadi, meskipun pada awalnya kami memilih hiperparameter yang buruk, setidaknya kami mengumpulkan informasi yang cukup untuk dapat meningkatkan pilihan parameter kami.

Secara umum, debugging NA adalah masalah yang rumit. Ini khususnya terjadi ketika pilihan hiperparameter awal menghasilkan hasil yang tidak melebihi noise acak. Misalkan kita mencoba menggunakan arsitektur 30 neuron yang berhasil, tetapi ubah kecepatan belajar menjadi 100.0:

 >>> net = network.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data) 

Pada akhirnya, ternyata kami terlalu jauh dan terlalu cepat:

Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000

Sekarang bayangkan kita sedang mendekati tugas ini untuk pertama kalinya. Tentu saja, kita tahu dari percobaan awal bahwa itu benar untuk mengurangi kecepatan belajar. Tetapi jika kita mendekati tugas ini untuk pertama kalinya, kita tidak akan memiliki output yang dapat membawa kita ke solusi yang tepat. Bisakah kita mulai berpikir bahwa mungkin kita telah memilih parameter awal yang salah untuk bobot dan offset, dan sulit bagi jaringan untuk belajar? Atau mungkin kita tidak memiliki data pelatihan yang cukup untuk mendapatkan hasil yang bermakna? Mungkin kita tidak menunggu era yang cukup? Mungkin jaringan saraf dengan arsitektur seperti itu tidak bisa belajar mengenali angka tulisan tangan? Mungkin kecepatan belajarnya terlalu lambat? Saat Anda pertama kali mendekati tugas, Anda tidak pernah memiliki kepercayaan diri.

Dari sini perlu dipelajari pelajaran bahwa men-debug NS bukan tugas yang sepele, dan ini, seperti pemrograman biasa, adalah bagian dari seni. Anda harus mempelajari seni debug ini untuk mendapatkan hasil yang baik dari NS. Secara umum, kita perlu mengembangkan heuristik untuk memilih hyperparameter dan arsitektur yang bagus. Kami akan membahas ini secara rinci dalam buku ini, termasuk bagaimana saya memilih hyperparameters di atas.

Latihan

• Cobalah untuk membuat jaringan hanya dua lapisan - input dan output, tanpa tersembunyi - masing-masing dengan 784 dan 10 neuron. Melatih jaringan dengan penurunan gradien stokastik. Apa akurasi klasifikasi yang Anda dapatkan?

Saya sebelumnya melewatkan detail memuat data MNIST. Itu terjadi cukup sederhana. Ini adalah kode untuk melengkapi gambar. Struktur data dijelaskan dalam komentar - semuanya sederhana, tupel dan larik objek Numpy ndarray (jika Anda tidak terbiasa dengan objek tersebut, anggap sebagai vektor).

 """ mnist_loader ~~~~~~~~~~~~      MNIST.       ``load_data``  ``load_data_wrapper``.  , ``load_data_wrapper`` -  ,     . """ ####  #  import cPickle import gzip #  import numpy as np def load_data(): """  MNIST   ,  ,    . ``training_data``      .    .  numpy ndarray  50 000 .   –     numpy ndarray  784 ,  28 * 28 = 784    MNIST.  –  numpy ndarray  50 000 .   –   0  9   ,    . ``validation_data``  ``test_data`` ,    10 000 .    ,           ``training_data``.    - ``load_data_wrapper()``. """ f = gzip.open('../data/mnist.pkl.gz', 'rb') training_data, validation_data, test_data = cPickle.load(f) f.close() return (training_data, validation_data, test_data) def load_data_wrapper(): """ ,  ``(training_data, validation_data, test_data)``.   ``load_data``,         .  , ``training_data`` -    50 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   . ``y`` -  10- numpy.ndarray,   ,     ``x``. ``validation_data``  ``test_data`` -  ,   10 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   ,  ``y`` -   ,  ,   ( ),  ``x``. ,  ,           .         .""" tr_d, va_d, te_d = load_data() training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]] training_results = [vectorized_result(y) for y in tr_d[1]] training_data = zip(training_inputs, training_results) validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]] validation_data = zip(validation_inputs, va_d[1]) test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]] test_data = zip(test_inputs, te_d[1]) return (training_data, validation_data, test_data) def vectorized_result(j): """ 10-    1.0   j     .      (0..9)     .""" e = np.zeros((10, 1)) e[j] = 1.0 return e 

Saya mengatakan bahwa program kami mencapai hasil yang cukup baik. Apa artinya ini? Bagus dibandingkan dengan apa? Adalah bermanfaat untuk mendapatkan hasil dari beberapa tes dasar yang sederhana yang dengannya Anda dapat membuat perbandingan untuk memahami apa arti "hasil yang baik". Level dasar yang paling sederhana, tentu saja, adalah tebakan acak. Ini dapat dilakukan pada sekitar 10% kasus. Dan kami menunjukkan hasil yang jauh lebih baik!

Bagaimana dengan tingkat dasar yang kurang sepele? Mari kita lihat seberapa gelap gambarnya. Misalnya, gambar 2 biasanya akan lebih gelap daripada gambar 1, hanya karena memiliki lebih banyak piksel gelap, seperti terlihat pada contoh di bawah ini:



Oleh karena itu kita dapat menghitung kegelapan rata-rata untuk setiap digit dari 0 hingga 9. Ketika kita mendapatkan gambar baru, kita menghitung kegelapannya, dan kami menduga itu menunjukkan angka dengan kegelapan rata-rata terdekat. Ini adalah prosedur sederhana yang mudah diprogram, jadi saya tidak akan menulis kode - jika tertarik, itu ada di GitHub . Tapi ini adalah peningkatan yang serius dibandingkan dengan tebakan acak - kode dengan benar mengenali 2.225 dari 10.000 gambar, yaitu memberikan akurasi 22,25%.

Tidak sulit untuk menemukan ide-ide lain yang mencapai akurasi dalam kisaran 20 hingga 50%. Setelah bekerja sedikit lagi, Anda dapat melebihi 50%. Tetapi untuk mencapai akurasi yang jauh lebih besar, lebih baik menggunakan algoritma MO otoritatif. Mari kita coba salah satu algoritma paling terkenal, metode vektor dukungan atau SVM. Jika Anda tidak terbiasa dengan SVM, jangan khawatir, kami tidak perlu memahami detail ini. Kami hanya menggunakan pustaka python bernama scikit-learn, yang menyediakan antarmuka sederhana ke pustaka C cepat untuk SVM, yang dikenal sebagai LIBSVM .

Jika kita menjalankan classifier SVM scikit-belajar pada pengaturan default, maka kita mendapatkan klasifikasi yang benar dari 9.435 dari 10.000 (kode tersedia di tautan) Ini sudah merupakan peningkatan besar atas pendekatan naif mengklasifikasikan gambar berdasarkan kegelapan. Ini berarti SVM bekerja sebaik NS kami, hanya sedikit lebih buruk. Dalam bab-bab berikut kita akan berkenalan dengan teknik-teknik baru yang akan memungkinkan kita untuk meningkatkan NS kita sehingga mereka jauh mengungguli SVM.

Tapi itu belum semuanya.Hasil 9 435 dari 10.000 dari scikit-learn ditentukan untuk pengaturan default. SVM memiliki banyak parameter yang dapat disetel, dan Anda dapat mencari parameter yang meningkatkan hasil ini. Saya tidak akan merinci, mereka dapat dibaca dalam artikel oleh Andreas Muller. Dia menunjukkan bahwa dengan melakukan pekerjaan untuk mengoptimalkan parameter, dimungkinkan untuk mencapai akurasi minimal 98,5%. Dengan kata lain, SVM yang disetel dengan baik hanya membuat satu digit dari 70 kesalahan. Hasil yang bagus! Bisakah NA mencapai lebih banyak?

Ternyata mereka bisa. Saat ini, NS yang telah disesuaikan dengan baik menyalip teknologi lain yang dikenal dalam solusi MNIST, termasuk SVM. Rekam untuk 2013diklasifikasikan dengan benar 9,979 dari 10.000 gambar. Dan kita akan melihat sebagian besar teknologi yang digunakan untuk ini dalam buku ini. Tingkat akurasi ini dekat dengan manusia, dan mungkin bahkan melebihi itu, karena beberapa gambar dari MNIST sulit diuraikan bahkan untuk manusia, misalnya: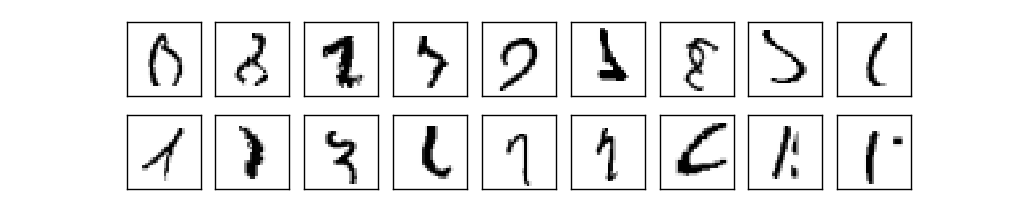



Saya pikir Anda akan setuju bahwa sulit untuk mengklasifikasikannya! Dengan gambar-gambar seperti itu dalam dataset MNIST, mengejutkan bahwa NS dapat dengan benar mengenali semua gambar dari 10.000, kecuali 21. Biasanya, programmer menganggap bahwa algoritma yang kompleks diperlukan untuk menyelesaikan tugas yang sedemikian rumit. Tetapi bahkan NS sedang bekerjapemegang catatan menggunakan algoritma yang cukup sederhana, yang merupakan variasi kecil dari yang kami periksa dalam bab ini. Semua kompleksitas muncul secara otomatis selama pelatihan berdasarkan data pelatihan. Dalam arti tertentu, moral hasil kami dan yang terkandung dalam karya yang lebih kompleks adalah untuk beberapa tugas

algoritme kompleks ≤ algoritma pelatihan sederhana + data pelatihan yang baik

Untuk pembelajaran yang mendalam

Meskipun jaringan kami menunjukkan kinerja yang mengesankan, itu dicapai dengan cara yang misterius. Bobot dan jaringan pencampuran terdeteksi secara otomatis. Jadi, kami tidak memiliki penjelasan siap pakai tentang bagaimana jaringan melakukan apa yang dilakukannya. Apakah ada cara untuk memahami prinsip dasar klasifikasi dengan jaringan angka tulisan tangan? Dan apakah mungkin, mengingat mereka, untuk meningkatkan hasilnya?

Kami merumuskan kembali pertanyaan-pertanyaan ini dengan lebih ketat: mari kita asumsikan bahwa dalam beberapa dekade NS akan berubah menjadi kecerdasan buatan (AI). Akankah kita mengerti bagaimana AI ini bekerja? Mungkin jaringan akan tetap tidak dapat dipahami oleh kami, dengan bobot dan offset mereka, karena mereka ditugaskan secara otomatis. Pada tahun-tahun awal penelitian AI, orang berharap bahwa mencoba membuat AI juga akan membantu kita memahami prinsip-prinsip yang mendasari kecerdasan, dan mungkin bahkan karya otak manusia. Namun, pada akhirnya mungkin kita tidak akan memahami otak atau cara kerja AI!

Untuk mengatasi masalah ini, mari kita ingat interpretasi neuron buatan yang saya berikan di awal bab ini - bahwa ini adalah cara untuk menimbang bukti. Misalkan kita ingin menentukan apakah wajah seseorang ada pada gambar:







Masalah ini dapat didekati dengan cara yang sama seperti pengenalan tulisan tangan: menggunakan piksel gambar sebagai input untuk NS, dan output dari NS akan menjadi satu neuron yang akan mengatakan, "Ya, ini wajah", atau "Tidak, ini bukan wajah ".

Misalkan kita melakukan ini, tetapi tanpa menggunakan algoritma pembelajaran. Kami akan mencoba membuat jaringan secara manual, memilih bobot dan offset yang sesuai. Bagaimana kita bisa mendekati ini? Untuk sesaat, lupa tentang Majelis Nasional, kita dapat membagi tugas menjadi subtugas: apakah gambar mata ada di sudut kiri atas? Apakah ada mata di sudut kanan atas? Apakah ada hidung tengah? Apakah ada mulut di tengah? Apakah ada rambut di bagian atas? Dan sebagainya.

Jika jawaban atas beberapa pertanyaan ini positif, atau bahkan "mungkin ya," maka kami menyimpulkan bahwa gambar tersebut mungkin memiliki wajah. Sebaliknya, jika jawabannya tidak, maka mungkin tidak ada orang.

Ini, tentu saja, adalah perkiraan heuristik, dan memiliki banyak kekurangan. Mungkin ini adalah pria botak, dan dia tidak memiliki rambut. Mungkin kita hanya bisa melihat sebagian wajah, atau wajah miring, sehingga beberapa bagian wajah tertutup. Namun demikian, heuristik menunjukkan bahwa jika kita dapat menyelesaikan submasalah dengan bantuan jaringan saraf, maka mungkin kita dapat membuat NS untuk pengenalan wajah dengan menggabungkan jaringan untuk subtugas. Berikut ini adalah arsitektur yang memungkinkan dari jaringan di mana subnet ditunjukkan oleh persegi panjang. Ini bukan pendekatan yang sepenuhnya realistis untuk memecahkan masalah pengenalan wajah: diperlukan untuk membantu kita secara intuitif memahami kerja jaringan saraf.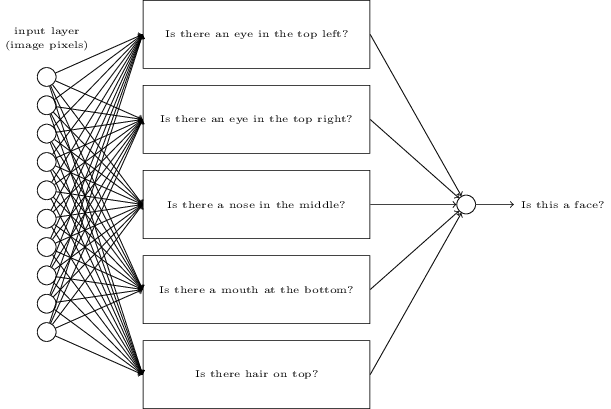


Dalam persegi panjang ada subtugas: apakah gambar mata ada di sudut kiri atas? Apakah ada mata di sudut kanan atas? Apakah ada hidung tengah? Apakah ada mulut di tengah? Apakah ada rambut di bagian atas? Dan sebagainya.

Ada kemungkinan bahwa subnet juga dapat dibongkar menjadi komponen. Ambil pertanyaan tentang memiliki mata di sudut kiri atas. Ini dapat dibedakan menjadi pertanyaan seperti: "Apakah ada alis?", "Apakah ada bulu mata?", "Apakah ada murid?" dan sebagainya. Tentu saja, pertanyaan harus berisi informasi tentang lokasi - "Apakah alis terletak di kiri atas, di atas murid?", Dan seterusnya - tetapi mari kita sederhanakan untuk sekarang. Oleh karena itu, jaringan yang menjawab pertanyaan tentang keberadaan mata dapat dibongkar menjadi komponen:


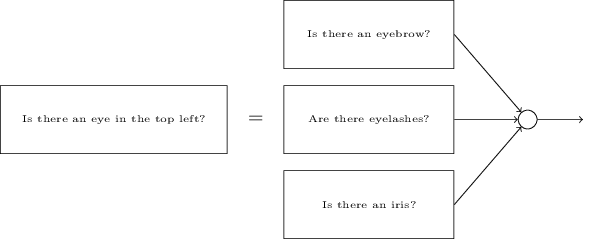"Apakah ada alis?", "Apakah ada bulu mata?", "Apakah ada murid?"

Pertanyaan-pertanyaan ini selanjutnya dapat dipecah menjadi pertanyaan-pertanyaan kecil, dalam langkah-langkah melalui banyak lapisan. Sebagai hasilnya, kami akan bekerja dengan subnet yang menjawab pertanyaan sederhana sedemikian rupa sehingga mudah dibongkar pada tingkat piksel. Pertanyaan-pertanyaan ini mungkin menyangkut, misalnya, ada tidaknya bentuk-bentuk sederhana di tempat-tempat gambar tertentu. Neuron individu yang terkait dengan piksel akan dapat meresponsnya.

Hasilnya adalah jaringan yang memecah pertanyaan yang sangat kompleks - apakah seseorang ada dalam gambar - menjadi pertanyaan yang sangat sederhana yang dapat dijawab pada tingkat piksel individu. Dia akan melakukan ini melalui serangkaian banyak lapisan, di mana lapisan pertama menjawab pertanyaan yang sangat sederhana dan spesifik tentang gambar, dan yang terakhir menciptakan hierarki konsep yang lebih kompleks dan abstrak. Jaringan dengan struktur multilayer - dua atau lebih lapisan tersembunyi - disebut deep neural networks (GNS).

Tentu saja, saya tidak berbicara tentang cara melakukan subnetting rekursif ini. Pasti tidak praktis untuk memilih bobot dan offset secara manual. Kami ingin menggunakan algoritma pelatihan sehingga jaringan secara otomatis mempelajari bobot dan offset - dan melaluinya hierarki konsep - berdasarkan data pelatihan. Para peneliti pada 1980-an dan 1990-an mencoba menggunakan keturunan gradien stokastik dan backpropagation untuk melatih GNS. Sayangnya, dengan pengecualian beberapa arsitektur khusus, mereka tidak berhasil. Jaringan dilatih, tetapi sangat lambat, dan dalam praktiknya terlalu lambat untuk digunakan entah bagaimana.

Sejak 2006, beberapa teknologi telah dikembangkan untuk melatih STS. Mereka didasarkan pada keturunan gradien stokastik dan propagasi kembali, tetapi mereka juga mengandung ide-ide baru. Mereka diizinkan untuk melatih jaringan yang lebih dalam - saat ini orang diam-diam melatih jaringan dengan 5-10 lapisan. Dan ternyata mereka memecahkan banyak masalah jauh lebih baik daripada NS dangkal, yaitu jaringan dengan satu lapisan tersembunyi. Alasannya, tentu saja, adalah bahwa STS dapat menciptakan hierarki konsep yang kompleks. Ini mirip dengan bagaimana bahasa pemrograman menggunakan skema modular dan ide-ide abstraksi sehingga mereka dapat membuat program komputer yang kompleks. Untuk membandingkan NS yang mendalam dengan NS yang dangkal adalah kira-kira bagaimana membandingkan bahasa pemrograman yang dapat membuat panggilan fungsi dengan bahasa yang tidak. Abstraksi di NS tidak terlihat seperti dalam bahasa pemrograman,tetapi memiliki kepentingan yang sama.