Apa itu probabilitas dan bagaimana cara menghitungnya

Biarkan ada beberapa eksperimen abstrak dalam proses yang mungkin terjadi peristiwa tertentu. Eksperimen ini dilakukan lima kali, dan di empat di antaranya acara yang sama terjadi. Kesimpulan apa yang bisa ditarik dari 4/5 ini?



Ada rumus Bernoulli yang memberikan jawaban dengan probabilitas 4 dari 5 yang terjadi dengan probabilitas awal yang diketahui. Tapi itu tidak memberikan jawaban, berapa probabilitas awal jika peristiwa ternyata menjadi 4 dari 5. Mari kita kesampingkan rumus Bernoulli.

Kami akan membuat program kecil sederhana yang mensimulasikan proses probabilitas untuk kasus seperti itu, dan berdasarkan hasil perhitungan kami membuat grafik.

void test1() { uint sz_ar_events = 50; //    uint ar_events[sz_ar_events]; //        for (uint i = 0; i < sz_ar_events; ++i) ar_events[i] = 0; uint cnt_events = 0; //       uint k = 4; // k   n  uint n = 5; //   while (cnt_events < 1000000) { //     // ,   0..1 double probability = get_random_real_0_1(); uint c_true = 0; for (uint i = 0; i < n; ++i) { //     probability, //  n-         bool v = get_true_with_probability(probability); if (v) ++c_true; } //   n-  k- ,      if (c_true == k) { uint idx = lrint(floor(probability*sz_ar_events)); assert( idx < sz_ar_events ); // ,      ++cnt_events; //   ++ar_events[idx]; //      } } //   for (uint i = 0; i < sz_ar_events; ++i) { double p0 = DD(i)/sz_ar_events; //  : //        double v = DD(ar_events[i])/cnt_events / (1.0/sz_ar_events); printf("%4.2f %f\n", p0, v); } } 

Kode untuk program ini dapat ditemukan di sini , bersama dengan fungsi tambahan.

Perhitungan dilemparkan ke Excel dan membuat jadwal.

Versi grafik ini dapat disebut distribusi kepadatan probabilitas dari nilai probabilitas. Luasnya sama dengan unit yang didistribusikan di gundukan ini.

Untuk melengkapi gambar, saya akan menyebutkan bahwa grafik ini sesuai dengan grafik menurut rumus Bernoulli dari parameter probabilitas dan dikalikan dengan N + 1 jumlah percobaan.

Lebih jauh dalam teks, di mana saya menggunakan sebagian kecil dari bentuk k / n dalam artikel, ini bukan divisi, ini adalah k peristiwa dari n percobaan, sehingga tidak menulis k dari n setiap kali.

Selanjutnya Dimungkinkan untuk meningkatkan jumlah percobaan, dan untuk mendapatkan wilayah yang lebih sempit dari lokasi nilai-nilai utama dari nilai probabilitas, tetapi tidak peduli bagaimana mereka ditingkatkan, wilayah ini tidak akan direduksi menjadi wilayah nol dengan probabilitas yang sudah diketahui.

Grafik di bawah ini menunjukkan distribusi untuk 4/5, 7/9, 11/14 dan 24/30. Semakin sempit area, semakin tinggi gundukannya, area yang merupakan unit konstan. Relasi ini dipilih karena semuanya sekitar 0,8, dan bukan karena justru inilah yang dapat muncul pada 0,8 dari probabilitas awal. Dipilih untuk mendemonstrasikan rentang nilai yang mungkin tetap ada dengan 30 percobaan dilakukan.

Kode program untuk grafik ini ada di sini .


Dari sini dapat disimpulkan bahwa dalam kenyataannya probabilitas eksperimental tidak dapat ditentukan secara tepat, tetapi kita hanya dapat mengasumsikan wilayah dari lokasi yang mungkin dari kuantitas tersebut, dengan akurasi tergantung pada berapa banyak pengukuran yang diambil.

Tidak peduli berapa banyak percobaan yang dilakukan, selalu ada kemungkinan bahwa probabilitas awal dapat berubah menjadi 0,0001 dan 0,9999. Untuk kesederhanaan, nilai ekstrim yang tidak mungkin dibuang. Dan kita ambil, katakanlah, misalnya 95% dari area utama dari jadwal distribusi.

Hal seperti itu disebut interval kepercayaan. Saya belum menemukan rekomendasi tentang berapa banyak dan mengapa bunga harus dibiarkan. Untuk perkiraan cuaca, kurangi waktu, untuk meluncurkan layanan antar-jemput ruang angkasa yang lebih banyak. Mereka juga biasanya tidak menyebutkan interval kepercayaan mana yang digunakan untuk probabilitas kejadian dan apakah digunakan sama sekali.

Dalam program saya, perhitungan batas interval kepercayaan dilakukan di sini .

Ternyata probabilitas peristiwa ditentukan oleh kepadatan probabilitas dari nilai probabilitas, dan masih perlu untuk memaksakan persentase area nilai-nilai utama di atasnya sehingga Anda setidaknya bisa mengatakan dengan pasti seperti apa probabilitas kejadian yang diteliti.

Sekarang, tentang percobaan yang lebih nyata.

Biarkan semua orang bosan dengan koin, lempar koin ini, dan dapatkan 4 dari 5 tetes demi tetes - kasus yang sangat nyata. Sebenarnya, ini tidak persis sama dengan yang dijelaskan sedikit lebih tinggi. Apa bedanya dengan eksperimen sebelumnya?

Eksperimen sebelumnya dijelaskan dengan asumsi bahwa probabilitas acara dapat didistribusikan secara merata selama interval dari 0 hingga 1. Dalam program ini, ini ditentukan oleh garis probabilitas ganda = get_random_real_0_1 (); . Tetapi tidak ada koin dengan kemungkinan jatuh, katakanlah, 0,1 atau 0,9 selalu di satu sisi.

Jika Anda mengambil seribu koin berbeda dari biasa hingga yang paling melengkung, dan untuk masing-masing melakukan pengukuran kerugian dengan melemparkannya seribu atau lebih kali, maka itu akan menunjukkan bahwa mereka benar-benar jatuh di satu sisi dalam kisaran 0,4 hingga 0,6 (ini adalah angka acak, saya tidak akan tapi saya mencari 1000 koin dan melemparkan setiap 1000 kali).

Bagaimana fakta ini mengubah program untuk mensimulasikan probabilitas satu koin tertentu, yang menerima 4 dari 5 ekor?

Misalkan distribusi kerugian di satu sisi untuk koin digambarkan sebagai perkiraan terhadap grafik distribusi normal yang diambil dengan parameter rata-rata = 0,5, standar deviasi = 0,1. (dalam grafik di bawah ini ditampilkan dalam warna hitam).

Ketika dalam sebuah program saya mengubah generasi probabilitas awal dari terdistribusi secara merata menjadi terdistribusi sesuai dengan aturan yang ditentukan, saya mendapatkan grafik berikut:


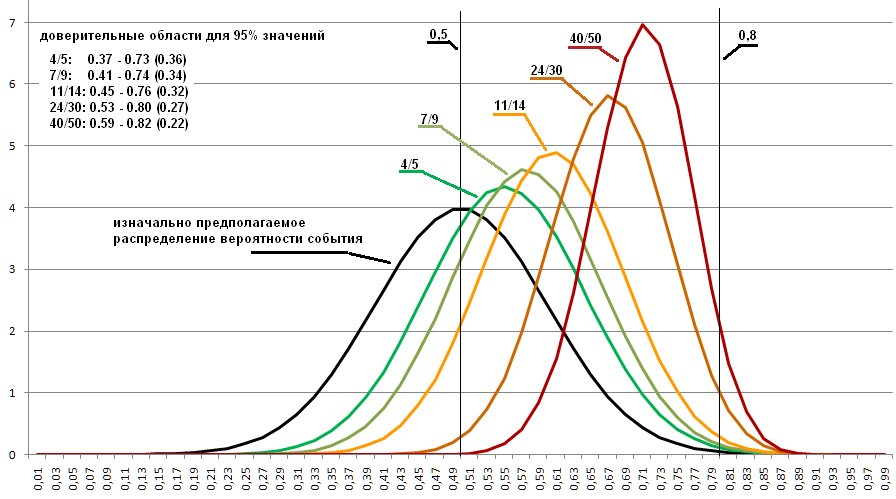
Kode untuk opsi ini ada di sini .

Dapat dilihat bahwa distribusi telah bergeser dengan kuat dan sekarang menentukan wilayah yang sedikit berbeda di mana probabilitas yang diinginkan sangat mungkin. Oleh karena itu, jika diketahui probabilitas apa yang ada untuk hal-hal itu, salah satunya yang ingin kita ukur, maka ini agak dapat meningkatkan hasilnya.

Akibatnya, 4/5 tidak berarti apa-apa, dan bahkan 50 percobaan yang dilakukan tidak terlalu informatif. Ini sangat sedikit informasi untuk menentukan probabilitas seperti apa yang masih mendasari percobaan.

== Perbarui ==

Seperti yang disebutkan dalam komentar, seseorang yang mengenal matematika secara signifikan, grafik ini juga dapat dibangun menggunakan rumus yang tepat. Tetapi tujuan dari artikel ini adalah untuk menunjukkan sejelas mungkin bagaimana apa yang disebut probabilitas setiap orang dalam kehidupan sehari-hari.

Untuk membangunnya menggunakan formula yang tepat, perlu untuk mempertimbangkan data yang tersedia tentang distribusi probabilitas semua koin melalui perkiraan distribusi beta, dan dengan menghitung distribusi, dapatkan perhitungan sudah. Skema semacam itu adalah sejumlah besar penjelasan tentang bagaimana melakukan ini, dan jika saya jelaskan di sini, itu akan menjadi artikel tentang perhitungan matematika, daripada probabilitas sehari-hari.

Cara mendapatkan formula yang dijelaskan kasus khusus dengan koin, lihat komentar dari jzha .