Properti simetri dari hubungan kointegrasi

Tujuan artikel ini adalah untuk berbagi hasil paradoks dalam studi ko-integrasi deret waktu : jika deret waktu $$$A$ terintegrasi dengan yang terdekat $$$B$ baris $$$B$ tidak selalu terintegrasi dengan angka $$$A$ .

Jika kita mempelajari kointegrasi murni secara teoritis, maka mudah untuk membuktikannya jika seri $$$A$ terintegrasi dengan $$$B$ lalu baris $$$B$ terintegrasi dengan $$$A$ . Namun, jika kita mulai mempelajari kointegrasi secara empiris, ternyata perhitungan teoretis tidak selalu dikonfirmasi. Mengapa ini terjadi?

Simetri

Sikap $$$A$ disebut symmetric if $$$A \ subseteq A ^ {- 1}$ dimana $$$A ^ {- 1}$ - rasio terbalik yang ditentukan oleh kondisi: $$$x A ^ {- 1} y$ sama saja dengan $$$yAx$ . Dengan kata lain, jika hubungannya $$$xAy$ lalu hubungannya $$$yAx$ .

Pertimbangkan dua $$$I (1)$ sejumlah $$$x_t$ dan $$$y_t$ , $$$t = 0, \ dots, T$ . Kointegrasi adalah simetris jika $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ mensyaratkan $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ yaitu, jika kehadiran regresi langsung mengarah ke kehadiran kebalikannya.

Pertimbangkan persamaannya $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ , $$$\ beta_1 \ neq 0$ . Tukar sisi kiri dan kanan dan kurangi $$$\ varepsilon_ {1t}$ dari kedua bagian: $$$\ beta_1 x_t = y_t - \ varepsilon_ {1t}$ . Sejak $$$\ beta_1 \ neq 0$ menurut definisi, bagi kedua bagian menjadi $$$\ beta_1$ :

$$

$$x_t = \ frac {1} {\ beta_1} y_t - \ frac {\ varepsilon_ {1t}} {\ beta_1}.$$

Ganti $$$1 / \ beta_1$ pada $$$\ beta_2$ , dan $$$- \ varepsilon_ {1t} / \ beta_1$ pada $$$\ varepsilon_ {2t}$ kita dapatkan $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ . Oleh karena itu, hubungan kointegrasi adalah simetris.

Oleh karena itu jika variabel $$$X$ terkointegrasi dengan variabel $$$Y$ lalu variabelnya $$$Y$ harus diintegrasikan bersama dengan variabel $$$X$ . Namun, tes kointegrasi Angle-Granger tidak selalu mengkonfirmasi properti simetri ini, karena kadang-kadang variabel $$$Y$ tidak terintegrasi dengan variabel $$$X$ menurut tes ini.

Saya menguji properti simetri pada data 2017 dari pertukaran Moskow dan New York menggunakan uji Angle-Granger. Ada 7.975 pasang saham co-terintegrasi di Bursa Moskow. Untuk 7731 (97%) pasangan terkointegrasi, properti simetri dikonfirmasi, untuk 244 (3%) pasangan terkointegrasi properti simetri tidak dikonfirmasi.

Ada 140.903 pasangan saham terintegrasi di New York Stock Exchange. Untuk 136586 (97%) pasangan terkointegrasi, properti simetri dikonfirmasi, untuk 4317 (3%) pasangan terkointegrasi properti simetri tidak dikonfirmasi.

Interpretasi

Hasil ini dapat ditafsirkan oleh daya rendah dan probabilitas kesalahan tinggi dari jenis kedua dari tes Dickey-Fuller, di mana tes Angle-Granger didasarkan. Probabilitas kesalahan jenis kedua dapat dilambangkan dengan $$$\ beta = P (H_0 | H_1)$ maka nilainya $$$1 - \ beta$ disebut kekuatan tes. Sayangnya, tes Dickey-Fuller tidak dapat membedakan antara deret waktu non-stasioner dan dekat-non-stasioner.

Apa itu deret waktu yang hampir tidak stabil? Pertimbangkan deret waktu $$$x_t = \ phi x_ {t-1} + \ varepsilon_t$ . Rangkaian waktu stasioner adalah seri di mana $$$0 <\ phi <1$ . Rangkaian waktu non-stasioner adalah seri di mana $$$\ phi = 1$ . Rangkaian waktu yang hampir tidak stabil adalah seri di mana nilainya $$$\ phi$ dekat dengan satu.

Dalam kasus deret waktu hampir tidak stasioner, kita sering tidak dapat menolak hipotesis nol dari stasioner. Ini berarti bahwa tes Dickey-Fuller memiliki risiko tinggi kesalahan jenis kedua, yaitu, probabilitas tidak menolak hipotesis nol palsu.

Tes KPSS

Sebuah tanggapan yang mungkin terhadap kelemahan dari tes Dickey-Fuller adalah tes KPSS, yang berutang namanya dengan inisial para ilmuwan Kvyatkovsky, Phillips, Schmidt dan Sheen. Meskipun pendekatan metodologis dari tes ini benar-benar berbeda dari pendekatan Dickey-Fuller, perbedaan utama harus dipahami dalam permutasi hipotesis nol dan alternatif.

Dalam tes KPSS, hipotesis nol menyatakan bahwa deret waktu stasioner, versus alternatif tentang keberadaan non-stasioneritas. Rangkaian waktu dekat-non-stasioner, yang sering diidentifikasi sebagai non-stasioner menggunakan tes Dickey-Fuller, dapat diidentifikasi dengan benar sebagai stasioner menggunakan uji KPSS.

Namun, kita harus sadar bahwa setiap hasil pengujian statistik hanyalah probabilistik dan tidak boleh dikacaukan dengan penilaian sejati tertentu. Selalu ada probabilitas nol untuk kita salah. Untuk alasan ini, diusulkan untuk menggabungkan hasil tes Dickey-Fuller dan KPSS sebagai tes ideal untuk non-stasioneritas.



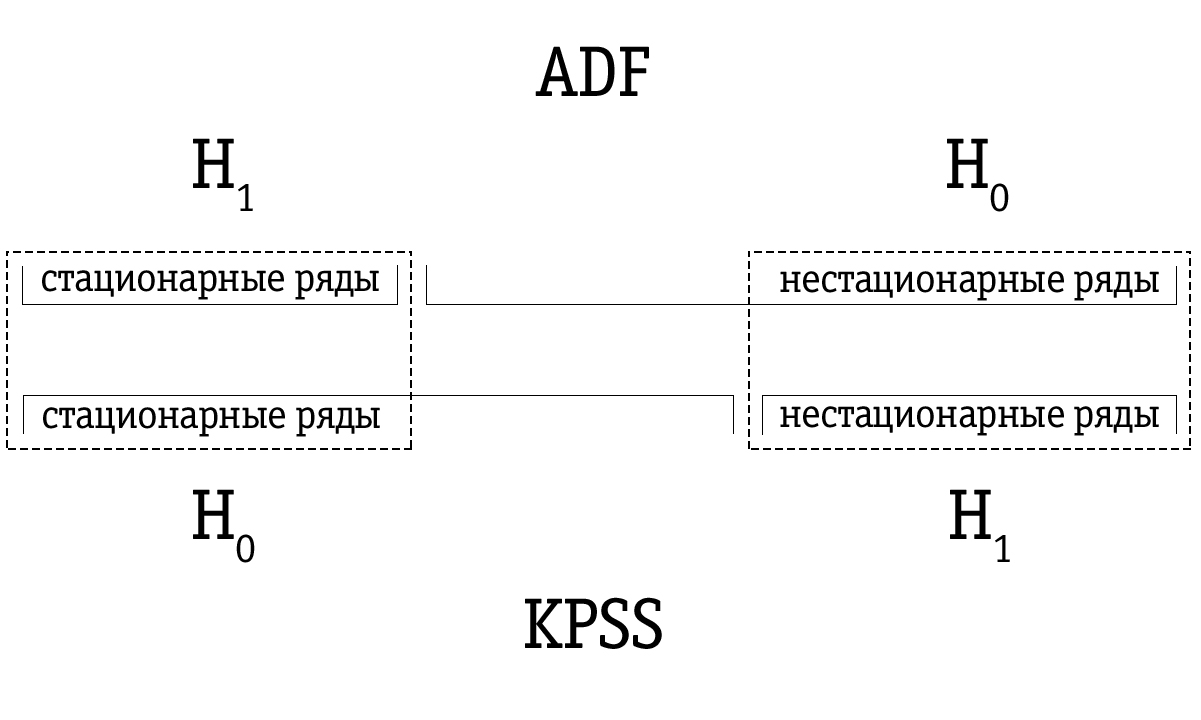
Karena daya yang rendah, tes Dickey-Fuller sering keliru mengidentifikasi seri sebagai non-stasioner, sehingga rangkaian waktu yang dihasilkan diidentifikasi oleh tes Dickey-Fuller sebagai tidak stabil ternyata lebih besar dibandingkan dengan banyak seri waktu yang diidentifikasi sebagai non-stasioner menggunakan tes KPSS. Oleh karena itu, urutan pengujian penting.

Jika deret waktu diidentifikasi sebagai stasioner menggunakan tes Dickey-Fuller, maka kemungkinan besar juga akan diidentifikasi sebagai stasioner menggunakan uji KPSS; dalam hal ini, kita dapat mengasumsikan bahwa seri ini memang stasioner.

Jika rangkaian waktu diidentifikasi tidak stabil menggunakan tes KPSS, maka kemungkinan besar juga akan diidentifikasi sebagai tidak stabil menggunakan uji Dickey-Fuller; dalam hal ini, kita dapat mengasumsikan bahwa seri ini memang tidak stabil.

Namun, sering terjadi bahwa rangkaian waktu yang telah diidentifikasi sebagai non-stasioner menggunakan tes Dickey-Fuller akan ditandai sebagai stasioner menggunakan tes KPSS. Dalam hal ini, kita harus sangat berhati-hati dengan kesimpulan akhir kita. Kita dapat memeriksa seberapa kuat dasar untuk stasioneritas dalam kasus tes KPSS dan ketidakstabilan dalam kasus tes Dickey-Fuller dan membuat keputusan yang tepat. Tentu saja, kita juga dapat meninggalkan pertanyaan tentang stasioneritas dari rangkaian waktu seperti itu yang tidak terselesaikan.

Pendekatan tes KPSS mengasumsikan deret waktu $$$y_t$ diuji untuk stasioneritas relatif terhadap tren dapat diuraikan menjadi jumlah tren deterministik $$$\ beta t$ jalan acak $$$r_t$ dan kesalahan stasioner $$$\ varepsilon_t$ :

$$

$$y_t = \ beta t + r_t + \ varepsilon_t, \\ r_t = r_ {t-1} + u_t,$$

dimana $$$u_t$ - proses normal iid dengan nol mean dan varians $$$\ sigma ^ 2$ ( $$$u_t \ sim N (0, \ sigma ^ 2)$ ) Nilai awal $$$r_0$ diperlakukan sebagai tetap dan memainkan peran sebagai anggota bebas. Kesalahan stasioner $$$\ varepsilon_t$ dapat dihasilkan oleh proses ARMA umum, yaitu, dapat memiliki autokorelasi yang kuat.

Mirip dengan tes Dickey-Fuller, kemampuan untuk memperhitungkan struktur autokorelasi sewenang-wenang $$$\ varepsilon_t$ sangat penting karena kebanyakan deret waktu ekonomi sangat tergantung waktu dan oleh karena itu memiliki autokorelasi yang kuat. Jika kita ingin memeriksa stasioneritas sehubungan dengan sumbu horizontal, maka istilah $$$\ beta t$ hanya dikecualikan dari persamaan di atas.

Dari persamaan di atas maka hipotesis nol $$$H_0$ tentang stasioneritas $$$y_t$ setara dengan hipotesis $$$\ sigma ^ 2 = 0$ , dari mana itu terjadi $$$r_t = r_0$ untuk semua $$$t$ ( $$$r_0$ Apakah konstan). Demikian pula hipotesis alternatif $$$H_1$ non-stasioneritas setara dengan hipotesis $$$\ sigma ^ 2 \ neq 0$ .

Untuk menguji hipotesis $$$H_0$ : $$$\ sigma ^ 2 = 0$ (seri waktu stasioner) versus alternatif $$$H_1$ : $$$\ sigma ^ 2 \ neq 0$ (seri waktu non-stasioner) penulis tes KPSS menerima statistik satu arah dari uji pengali Lagrange. Mereka juga menghitung distribusi asimptotik dan memodelkan nilai kritis asimptotik. Kami tidak mempertimbangkan detail teoretis di sini, tetapi hanya menguraikan secara singkat algoritme pelaksanaan pengujian.

Saat melakukan tes KPSS untuk serangkaian waktu $$$y_t$ , $$$t = 1, \ dots, T$ metode kuadrat terkecil (kuadrat terkecil) digunakan untuk memperkirakan salah satu persamaan berikut:

$$

$$y_t = a_0 + \ varepsilon_t, \\ y_t = a_0 + \ beta t + \ varepsilon_t.$$

Jika kita ingin memeriksa stasioneritas sehubungan dengan sumbu horizontal, kita mengevaluasi persamaan pertama. Jika kami berencana untuk memeriksa stasioneritas sehubungan dengan tren, kami memilih persamaan kedua.

Sisa makanan $$$e_t$ dari persamaan estimasi digunakan untuk menghitung statistik uji pengganda Lagrange. Tes pengali Lagrange didasarkan pada gagasan bahwa ketika hipotesis nol terpenuhi, semua pengali Lagrange harus sama dengan nol.

Tes pengali lagrange

Tes pengali Lagrange dikaitkan dengan pendekatan yang lebih umum untuk estimasi parameter menggunakan metode kemungkinan maksimum (ML). Menurut pendekatan ini, data dianggap sebagai bukti yang terkait dengan parameter distribusi. Bukti dinyatakan sebagai fungsi dari parameter yang tidak diketahui - fungsi kemungkinan:

$$

$$L (X_1, X_2, X_3, \ dots, X_n; \ Phi_1, \ Phi_2, \ dots, \ Phi_k),$$

dimana $$$X_i$ Apakah nilai yang diamati, dan $$$\ Phi_i$ - parameter yang ingin kita evaluasi.

Fungsi kemungkinan maksimum adalah probabilitas gabungan dari pengamatan sampel.

$$

$$L (X_1, X_2, X_3, \ dots, X_n; \ Phi_1, \ Phi_2, \ dots, \ Phi_k) = P (X_1 \ land X_2 \ land X_3 \ dots X_n).$$

Tujuan dari metode kemungkinan maksimum adalah untuk memaksimalkan fungsi kemungkinan. Ini dicapai dengan membedakan fungsi probabilitas maksimum untuk masing-masing parameter yang diestimasi dan menyamakan derivatif parsial ke nol. Nilai parameter di mana nilai fungsi maksimum adalah perkiraan yang diinginkan.

Biasanya, untuk menyederhanakan pekerjaan selanjutnya, logaritma fungsi kemungkinan pertama kali diambil.

Pertimbangkan model linier umum $$$Y = \ beta X + \ varepsilon$ dimana diasumsikan itu $$$\ varepsilon$ terdistribusi secara normal $$$N (0, \ sigma ^ 2)$ itu adalah $$$Y - \ beta X \ sim N (0, \ sigma ^ 2)$ .

Kami ingin menguji hipotesis bahwa sistem $$$q$ ( $$$q <k$ ) kendala linier independen $$$R \ beta = r$ . Di sini $$$R$ - terkenal $$$q \ kali k$ matriks peringkat $$$q$ , dan $$$r$ - terkenal $$$q \ kali 1$ vektor.

Untuk setiap pasangan nilai yang diamati $$$X$ dan $$$Y$ dalam kondisi normal, fungsi kerapatan probabilitas dari bentuk berikut akan ada:

$$

$$f (X_i, Y_i) = \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ kiri (\ frac {Y_i - \ beta X_i} {\ sigma} \ kanan) ^ 2}.$$

Tunduk pada $$$n$ pengamatan bersama $$$X$ dan $$$Y$ probabilitas total untuk mengamati semua nilai dalam sampel sama dengan produk dari nilai individu dari fungsi kepadatan probabilitas. Dengan demikian, fungsi kemungkinan didefinisikan sebagai berikut:

$$

$$L (\ beta) = \ prod \ Limit_ {i = 1} ^ n \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ kiri (\ frac {Y_i - \ beta X_i} {\ sigma} \ kanan) ^ 2}.$$

Karena lebih mudah untuk membedakan jumlah dari produk, logaritma fungsi kemungkinan biasanya diambil, dengan demikian:

$$

$$\ ln L (\ beta) = \ jumlah \ limit_ {i = 1} ^ n \ kiri (\ ln \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} - \ frac {1} { 2 \ sigma ^ 2} (Y_i - \ beta X_i) ^ 2 \ kanan).$$

Konversi yang bermanfaat ini tidak memengaruhi hasil akhir, karena $$$\ ln L$ Merupakan fungsi yang meningkat $$$L$ . Jadi nilainya $$$\ beta$ yang memaksimalkan $$$\ ln L$ juga akan memaksimalkan $$$L$ .

Skor ML untuk $$$\ beta$ dalam regresi dengan batasan ( $$$R \ beta = r$ ) diperoleh dengan memaksimalkan fungsi $$$\ ln L (\ beta)$ tunduk pada $$$R \ beta = r$ . Untuk menemukan perkiraan ini, kami menulis fungsi Lagrange:

$$

$$\ psi (\ beta) = \ ln L (\ beta) - g '(R \ beta - r),$$

dimana lewat $$$g = \ kiri (g_1, \ dots, g_q \ right) '$ vektor bertanda $$$q$ Pengganda lagrange.

Statistik uji pengali lagrange dilambangkan dengan $$$\ eta_ \ mu$ dalam hal stasioneritas sehubungan dengan sumbu horisontal dan melalui $$$\ eta_ \ tau$ dalam hal stasioneritas relatif terhadap tren, itu ditentukan oleh ekspresi

$$

$$\ eta _ {\ mu / \ tau} = T ^ 2 \ frac {1} {s ^ 2 (l)} \ jumlah \ limit_ {t = 1} ^ T S_t ^ 2,$$

dimana

$$

$$S_t = \ jumlah \ limit_ {i = 1} ^ t e_i$$

dan

$$

$$s ^ 2 (l) = T ^ {- 1} \ jumlah \ limit_ {t = 1} ^ T e_t ^ 2 + 2 T ^ {- 1} \ jumlah \ limit_ {1} ^ lw (s, l) \ jumlah \ limit_ {t = s + 1} ^ T e_t e_ {ts},$$

dimana

$$

$$w (s, l) = 1 - \ frac {s} {l + 1}.$$

Dalam persamaan di atas $$$S_t$ - proses saldo parsial $$$e_t$ dari estimasi persamaan; $$$s ^ 2 (l)$ - penilaian dispersi residu jangka panjang $$$e_t$ ; tapi $$$w (s, l)$ - jendela spektral yang disebut Bartlett, di mana $$$l$ - parameter pemotongan lag.

Dalam aplikasi ini, jendela spektral digunakan untuk memperkirakan kerapatan spektral kesalahan untuk interval tertentu (jendela), yang bergerak di sepanjang seluruh rentang seri. Data di luar interval diabaikan, karena fungsi jendela adalah fungsi yang sama dengan nol di luar beberapa interval yang dipilih (jendela).

Estimasi Varians $$$s ^ 2 (l)$ tergantung pada parameternya $$$l$ , dan sejak itu $$$l$ meningkat dan lebih dari 0, skor $$$s ^ 2 (l)$ mulai mempertimbangkan kemungkinan autokorelasi dalam residu $$$e_t$ .

Akhirnya, statistik uji pengali Lagrange $$$\ eta_ \ mu$ atau $$$\ eta_ \ tau$ bandingkan dengan nilai kritis. Jika statistik uji pengali Lagrange melebihi nilai kritis yang sesuai, maka hipotesis nol $$$H_0$ (Rangkaian waktu stasioner) menyimpang mendukung hipotesis alternatif $$$H_1$ (seri waktu non-stasioner). Kalau tidak, kita tidak bisa menolak hipotesis nol $$$H_0$ tentang stasioneritas dari deret waktu.

Nilai kritis asimptotik dan, karenanya, paling cocok untuk ukuran sampel besar. Namun, dalam praktiknya mereka juga digunakan untuk sampel kecil. Selain itu, nilai kritis tidak tergantung pada parameter $$$l$ . Namun, statistik uji pengali Lagrange akan tergantung pada parameter $$$l$ . Penulis tes KPSS tidak menawarkan algoritma umum untuk memilih parameter yang sesuai. $$$l$ . Tes biasanya dilakukan untuk $$$l$ dalam kisaran 0 hingga 8.

Dengan peningkatan $$$l$ kita cenderung menolak hipotesis nol $$$H_0$ tentang stasioneritas, yang sebagian mengarah pada penurunan kekuatan tes dan dapat memberikan hasil yang beragam. Namun, secara umum, kita dapat mengatakan bahwa jika hipotesis nol $$$H_0$ stasioneritas dari deret waktu tidak ditolak bahkan pada nilai yang kecil $$$l$ (0, 1 atau 2), kami menyimpulkan bahwa seri waktu yang diverifikasi adalah stasioner.

Perbandingan Hasil Tes

Metodologi berikut dikembangkan untuk menilai kemungkinan simetri.

1. Semua seri waktu diperiksa untuk keterpaduan urutan pertama menggunakan uji Dickey-Fuller pada tingkat signifikansi 0,05. Hanya seri yang dapat diintegrasikan dari urutan pertama yang dipertimbangkan di bawah ini.
2. Seri keterpaduan orde pertama yang diperoleh pada Bagian 1 terdiri dari pasangan dengan menggabungkan tanpa pengulangan.
3. Pasangan saham yang dibuat pada klausa 2 diuji untuk kointegrasi menggunakan uji Angle-Granger. Sebagai hasilnya, pasangan terkointegrasi diidentifikasi.
4. Residu regresi yang diperoleh sebagai hasil pengujian pada paragraf 3 diuji untuk stasioneritas menggunakan tes KPSS. Dengan demikian, hasil dari dua tes tersebut digabungkan.
5. Rangkaian waktu dalam pasangan co-terintegrasi dari item 2 dipertukarkan dan diperiksa lagi untuk co-integrasi menggunakan uji Angle-Granger, yaitu, kami memeriksa apakah hubungan antara seri waktu adalah simetris.
6. Rangkaian waktu dalam pasangan co-terintegrasi dari item 4 dipertukarkan dan residu dari regresi diperiksa lagi untuk stasioneritas menggunakan tes KPSS, yaitu, kita akan memeriksa apakah hubungan antara seri waktu simetris.

Semua perhitungan dilakukan dengan menggunakan paket MATLAB. Hasilnya disajikan dalam tabel di bawah ini. Untuk setiap tes, kami memiliki sejumlah hubungan yang simetris sesuai dengan hasil tes (ditandai $$$S$ ); kami memiliki sejumlah hubungan yang tidak simetris sesuai dengan hasil pengujian (ditandai $$$¬S$ ); dan kami memiliki probabilitas empiris bahwa rasio tersebut simetris sesuai dengan hasil tes ( $$$P (S) = \ frac {S} {S + ¬S}$ )

Di Bursa Moskow:


Di Bursa Efek New York:

Perbandingan Hasil Backtest

Mari kita bandingkan hasil strategi perdagangan pada data historis untuk pasangan co-terintegrasi yang dipilih menggunakan uji Angle-Granger dan untuk pasangan co-terintegrasi yang dipilih menggunakan tes KPSS.

Seperti dapat dilihat dari tabel, karena identifikasi yang lebih akurat dari pasangan saham co-terintegrasi, itu mungkin untuk meningkatkan hasil tahunan rata-rata ketika perdagangan pasangan co-terintegrasi yang terpisah sebesar 9,21%. Dengan demikian, metodologi yang diusulkan dapat meningkatkan profitabilitas perdagangan algoritmik menggunakan strategi pasar-netral.

Interpretasi alternatif

Seperti yang kita lihat di atas, hasil uji Angle-Granger adalah lotere. Bagi sebagian orang, pikiran saya akan tampak terlalu kategoris, tetapi saya pikir sangat masuk akal untuk tidak mengambil hipotesis nol, yang dikonfirmasi oleh analisis statistik, tentang iman.

Konservatisme dari metode ilmiah untuk menguji hipotesis adalah bahwa ketika menganalisis data kita hanya dapat membuat satu kesimpulan yang valid: hipotesis nol ditolak pada tingkat signifikansi yang dipilih. Ini tidak berarti bahwa alternatif itu benar. $$$H_1$ - kami baru saja menerima bukti tidak langsung kredibilitasnya berdasarkan "bukti dari sebaliknya" yang khas. Dalam kasus ketika itu benar $$$H_0$ , peneliti juga diinstruksikan untuk membuat kesimpulan yang hati-hati: berdasarkan data yang diperoleh dalam kondisi eksperimental, itu tidak mungkin untuk menemukan cukup bukti untuk menolak hipotesis nol.

Bersamaan dengan pemikiran saya pada bulan September 2018, sebuah artikel ditulis oleh orang-orang berpengaruh yang mendesak untuk meninggalkan konsep "signifikansi statistik" dan paradigma pengujian hipotesis nol.

Yang paling penting: “Saran seperti mengubah level ambang batas $$$p$ -nilai default, penggunaan interval kepercayaan dengan penekanan pada apakah mereka mengandung nol atau tidak, atau penggunaan koefisien Bayes bersama dengan klasifikasi yang diterima secara universal untuk menilai kekuatan bukti yang datang dari semua masalah yang sama atau mirip seperti penggunaan saat ini $$$p$ -nilai dengan tingkat 0,05 ... adalah bentuk alkimia statistik yang membuat janji palsu untuk mengubah keacakan menjadi keandalan, yang disebut "pencucian ketidakpastian" (Gelman, 2016), yang dimulai dengan data dan berakhir dengan kesimpulan dikotomis tentang kebenaran atau kepalsuan - pernyataan biner bahwa “ada efek” atau “tidak ada efek” - atas dasar pencapaian beberapa $$nilai p atau nilai ambang lainnya. Langkah kritis ke depan adalah penerimaan ketidakpastian dan variabilitas efek (Carlin, 2016; Gelman, 2016), pengakuan bahwa kita dapat belajar lebih banyak (lebih banyak) tentang dunia, meninggalkan janji keliru kepastian yang ditawarkan oleh dikotomisasi semacam itu. ”$p$

Kesimpulan

Kami melihat bahwa meskipun properti simetri dari hubungan kointegrasi secara teori harus dipenuhi, data eksperimen berbeda dari perhitungan teoritis. Salah satu interpretasi dari paradoks ini adalah rendahnya daya ujian Dickey-Fuller.

Sebagai metodologi baru untuk mengidentifikasi pasangan aset terintegrasi, diusulkan untuk menguji residu regresi yang diperoleh dengan menggunakan uji Angle-Granger untuk stasioneritas menggunakan uji KPSS dan menggabungkan hasil tes ini; dan menggabungkan hasil uji Angle-Granger dan tes KPSS untuk regresi langsung dan mundur.

Backtests dilakukan pada data Bursa Moskow untuk 2017. Menurut hasil backtests, hasil tahunan rata-rata ketika menggunakan metodologi untuk mengidentifikasi pasangan saham terkointegrasi yang diusulkan di atas adalah 22,72%. Dengan demikian, dibandingkan dengan identifikasi pasangan saham terintegrasi menggunakan uji Angle-Granger, adalah mungkin untuk meningkatkan hasil tahunan rata-rata sebesar 9,21%.

Interpretasi alternatif dari paradoks adalah untuk tidak mengambil hipotesis nol, yang dikonfirmasi oleh analisis statistik, tentang iman. Paradigma pengujian hipotesis nol dan dikotomi yang ditawarkan oleh paradigma seperti itu memberi kita pengertian yang salah tentang pengetahuan pasar.

Ketika saya baru saja memulai penelitian saya, tampak bagi saya bahwa Anda dapat mengambil pasar, memasukkannya ke dalam "penggiling daging" dari uji statistik dan mendapatkan barisan lezat yang disaring di pintu keluar. Sayangnya, sekarang saya melihat bahwa konsep brute force statistik ini tidak akan berfungsi.

Apakah ada kointegrasi di pasar atau tidak - bagi saya pertanyaan ini tetap terbuka. Saya masih memiliki pertanyaan besar untuk para pendiri teori ini. Dulu saya memiliki kegelisahan di Barat dan para ilmuwan yang mengembangkan matematika keuangan pada saat ekonometrik dianggap sebagai borjuis korup di Uni Soviet. Tampak bagi saya bahwa kami sangat jauh di belakang, dan di suatu tempat di Eropa dan Amerika para dewa keuangan sedang duduk, yang tahu cawan kebenaran yang sakral.

Sekarang saya mengerti bahwa para ilmuwan Eropa dan Amerika tidak jauh berbeda dari kita, satu-satunya perbedaan adalah dalam skala perdukunan. Para ilmuwan kami duduk di kastil gading, mereka menulis omong kosong dan menerima hibah dalam jumlah 500 ribu rubel. Di Barat, tentang para ilmuwan yang sama yang duduk di sekitar kastil gading yang sama, mereka menulis tentang omong kosong yang sama dan mendapatkan "nobel" dan hibah dalam jumlah 500 ribu dolar untuk ini. Itulah perbedaan keseluruhan.

Saat ini, saya tidak memiliki pandangan yang jelas tentang subjek penelitian saya. Adalah salah untuk mengatakan bahwa “semua dana lindung nilai menggunakan perdagangan pasangan” karena sebagian besar dana lindung nilai juga bangkrut.

Sayangnya, Anda selalu harus berpikir dan membuat keputusan dengan kepala Anda sendiri, terutama ketika kita mengambil risiko uang.