Pemrograman dinamis memiliki reputasi untuk metode yang Anda pelajari di universitas, dan kemudian hanya mengingat selama wawancara. Namun pada kenyataannya, metode ini berlaku dalam banyak situasi. Sebenarnya, ini adalah teknik untuk memecahkan masalah secara efektif yang dapat dibagi menjadi banyak subtugas yang sangat berulang .

Dalam artikel ini saya akan menunjukkan aplikasi nyata yang menarik dari pemrograman dinamis - tugas mengukir jahitan. Tugas dan metodologi dijelaskan secara rinci dalam karya Avidan dan Shamir "Memotong jahitan untuk mengubah ukuran gambar berdasarkan konten" (artikel dalam domain publik).

Ini adalah salah satu dari serangkaian artikel tentang pemrograman dinamis. Jika Anda ingin memoles metode, lihat pengantar bergambar untuk pemrograman dinamis .

Ubah ukuran gambar berdasarkan konten

Untuk memecahkan masalah nyata menggunakan pemrograman dinamis, Anda perlu merumuskannya dengan benar. Bagian ini menjelaskan pengaturan awal yang diperlukan untuk tugas yang dipilih.

Para penulis artikel asli menggambarkan pengubahan ukuran gambar yang berorientasi konten, yaitu mengubah lebar atau tinggi gambar berdasarkan konten. Lihat karya asli untuk detailnya, dan saya menawarkan tinjauan singkat. Misalkan Anda ingin mengubah ukuran foto peselancar:

Pemandangan terbaik dari seorang surfer di tengah samudra yang tenang, dengan ombak yang bergolak di sebelah kanan. Foto: Kiril Dobrev di Pixabay

Seperti dijelaskan secara rinci dalam artikel, ada beberapa cara untuk mengurangi lebar gambar: ini adalah pemotongan standar dan penskalaan, dengan kelemahan bawaannya, serta menghilangkan kolom piksel dari tengah. Seperti yang dapat Anda bayangkan, ini meninggalkan jahitan yang terlihat di foto, di mana gambar di kiri dan kanan tidak cocok. Dan dengan cara ini, Anda hanya dapat menghapus gambar dalam jumlah terbatas.

Upaya untuk mengurangi lebar dengan memotong sisi kiri dan memotong blok keluar dari tengah. Yang terakhir meninggalkan jahitan yang terlihat.

Avidan dan Shamir dalam artikel tersebut menggambarkan teknik baru "ukiran jahitan". Pertama-tama mengidentifikasi area "energi rendah" yang kurang penting, dan kemudian menghitung "lapisan" energi rendah yang melewati gambar. Dalam hal mengurangi lebar gambar, jahitan vertikal ditentukan dari atas gambar ke bawah, yang pada setiap baris bergerak tidak lebih dari satu piksel ke kiri atau ke kanan.

Dalam foto surfer, lapisan energi terendah mengalir di tengah-tengah gambar, di mana air adalah yang paling tenang. Ini konsisten dengan intuisi kita.

Jahitan berenergi terendah yang ditemukan pada gambar surfer ditunjukkan dengan garis merah lima piksel lebar untuk visibilitas, meskipun sebenarnya jahitannya hanya selebar satu piksel.

Setelah menentukan jahitan dengan energi paling sedikit, dan kemudian melepasnya, kami mengurangi lebar gambar dengan satu piksel. Mengulangi proses ini berulang kali secara signifikan mengurangi lebar seluruh foto.

Surfer gambar setelah pengurangan lebar 1024 piksel

Sekali lagi, algoritma secara logis menghilangkan air diam di tengah, serta di sisi kiri foto. Tetapi tidak seperti tanam, tekstur air di sebelah kiri dipertahankan dan tidak ada transisi yang tajam. Benar, Anda dapat menemukan beberapa transisi yang tidak sempurna di tengah, tetapi pada dasarnya hasilnya terlihat alami.

Definisi Energi Gambar

Keajaibannya adalah menemukan lapisan energi terendah. Untuk melakukan ini, pertama-tama kami menetapkan energi untuk setiap piksel dalam gambar. Kemudian kami menggunakan pemrograman dinamis untuk menemukan jalur melalui gambar dengan energi paling sedikit - algoritma ini akan dibahas secara rinci di bagian selanjutnya. Pertama, mari kita lihat cara menetapkan nilai energi piksel.

Artikel ilmiah ini membahas beberapa fungsi energi dan perbedaannya. Mari kita tidak menyulitkannya dan mengambil fungsi yang hanya menangkap jumlah perubahan warna di sekitar setiap piksel. Untuk melengkapi gambar, saya akan menjelaskan fungsi energi secara lebih terperinci jika Anda ingin mengimplementasikannya sendiri, tetapi ini hanyalah preset untuk perhitungan pemrograman dinamis berikutnya.

Di sebelah kiri ada tiga piksel dari gelap ke terang. Perbedaan antara yang pertama dan yang terakhir itu hebat. Tiga piksel gelap di sebelah kanan dengan sedikit perbedaan dalam intensitas warna

Untuk menghitung energi piksel tertentu, lihat piksel di sebelah kiri dan kanannya. Dari segi komponen, kami menghitung kuadrat jarak di antara mereka, yaitu kuadrat perbedaan antara komponen merah, hijau, dan biru, dan kemudian menambahkannya. Kami melakukan hal yang sama untuk piksel di atas dan di bawah tengah. Akhirnya, tambahkan jarak horizontal dan vertikal.

| D e l t a x |^{2} = (D e l t a r_{x})^{2} + (D e l t a g_{x})^{2} + (D e l t a b_{x})^{2}

$| \ Delta x | ^ 2 = (\ Delta r_x) ^ 2 + (\ Delta g_x) ^ 2 + (\ Delta b_x) ^ 2$

| D e l t a y |^{2} = (D e l t a r_{y})^{2} + (D e l t a g_{y})^{2} + (D e l t a b_{y})^{2}

$| \ Delta y | ^ 2 = (\ Delta r_y) ^ 2 + (\ Delta g_y) ^ 2 + (\ Delta b_y) ^ 2$

e (x, y) = | D e l t a x |^{2} + | D e l t a y |^{2}

$e (x, y) = | \ Delta x | ^ 2 + | \ Delta y | ^ 2$

Satu-satunya peringatan - katakanlah, jika sebuah piksel berada di tepi kiri, maka tidak ada tetangga di sebelah kiri. Dalam hal ini, kami membandingkan hanya dengan piksel yang tepat. Pemeriksaan serupa dilakukan untuk piksel di tepi atas, kanan, dan bawah.

Fungsi energi sangat bagus jika piksel tetangga memiliki warna yang sangat berbeda, dan kecil jika mirip.

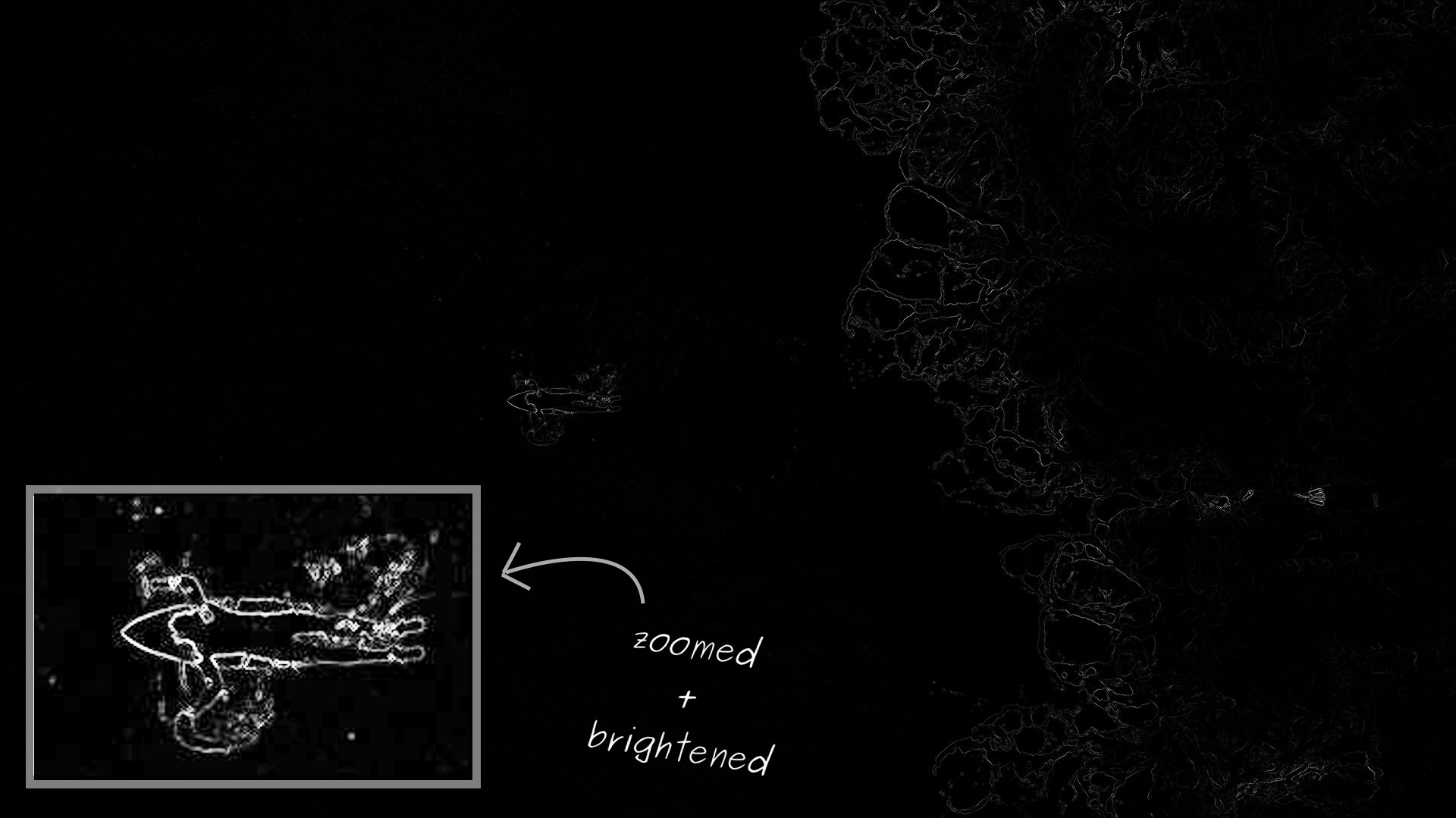Energi setiap piksel dalam foto surfer: semakin terang - semakin tinggi. Seperti yang diharapkan, surfer memiliki energi tertinggi di tengah dan gelombang yang bergolak di sebelah kanan

Fungsi energi bekerja dengan baik pada foto surfer. Namun, dibutuhkan rentang nilai yang sangat luas. Oleh karena itu, ketika merender, tampaknya sebagian besar foto memiliki energi nol. Bahkan, ada nilai yang sangat rendah dibandingkan dengan daerah dengan energi tertinggi. Untuk menyederhanakan visualisasi, saya memperbesar surfer dan menyoroti area ini.

Cari lapisan berenergi rendah dengan pemrograman dinamis

Dengan menghitung energi setiap piksel, kita dapat menemukan lapisan dengan energi terendah dari atas gambar ke bawah. Analisis yang sama berlaku untuk lapisan horizontal untuk mengurangi ketinggian gambar asli. Namun, kami akan fokus pada yang vertikal.

Mari kita mulai dengan definisi:

Jahitan adalah urutan piksel, satu piksel per baris. Syaratnya adalah bahwa antara dua garis berturut-turut koordinat $x$ perubahan tidak lebih dari satu piksel. Ini mempertahankan urutan jahitan.
Lapisan dengan energi terendah adalah yang total energinya di atas semua piksel pada lapisan diminimalkan.

Penting untuk dicatat bahwa sambungan dengan energi terendah tidak harus melalui semua piksel dengan energi terendah. Energi total semua, bukan piksel individual, diperhitungkan.

Pendekatan serakah tidak berhasil. Memilih piksel berenergi rendah pada tahap awal, kami terjebak di wilayah berenergi tinggi pada gambar (jalur merah ke kanan)

Seperti yang Anda lihat, Anda tidak bisa hanya memilih piksel energi terendah di baris berikutnya.

Kami memecah masalah menjadi subtugas

Masalah dengan pendekatan serakah adalah bahwa ketika memutuskan langkah selanjutnya, kita tidak memperhitungkan sisa jahitan di depan. Kita tidak bisa melihat ke masa depan, tetapi kita bisa memperhitungkan segala yang sudah kita ketahui sekarang.

Mari kita membalikkan tugas. Alih-alih memilih antara beberapa piksel untuk melanjutkan satu jahitan, kami akan memilih antara beberapa jahitan untuk pergi ke satu piksel . Apa yang perlu kita lakukan adalah mengambil setiap piksel dan memilih antara piksel pada baris di atas, dari mana jahitan dapat berasal. Jika masing-masing piksel pada baris di atas mengkodekan jalur yang dilalui ke titik ini, maka pada dasarnya kami sedang melihat riwayat lengkap ke titik ini.

Untuk setiap piksel, kami mempelajari tiga piksel pada baris di atas. Pilihan mendasar - mana dari jahitan untuk melanjutkan?

Ini mengasumsikan subtugas untuk setiap piksel dalam gambar. Subtugas harus menemukan jalur terbaik ke piksel tertentu, jadi itu ide yang baik untuk mengasosiasikan dengan setiap piksel energi dari lapisan energi rendah yang berakhir pada piksel itu .

Berbeda dengan pendekatan serakah, pendekatan di atas pada dasarnya mencoba semua jalur yang mungkin melalui gambar. Hanya saja ketika memeriksa semua jalur yang mungkin, subtugas yang sama diselesaikan berulang-ulang, yang menjadikan pendekatan ini pilihan ideal untuk pemrograman dinamis.

Definisi relasi perulangan

Seperti biasa, sekarang kita perlu memformalkan ide dalam hubungan rekursif. Ada subtugas yang sesuai dengan masing-masing piksel dalam gambar asli, sehingga input untuk relasi perulangan kami bisa hanya koordinat

x

$x$ dan

y

$y$ dari piksel ini. Ini memberikan input integer, membuatnya mudah untuk mengatur subtugas, serta kemampuan untuk menyimpan nilai yang dihitung sebelumnya dalam array dua dimensi.

Tentukan fungsi

M (x, y)

$M (x, y)$ , Yang mewakili energi dari jahitan vertikal dengan energi paling sedikit. Dimulai di bagian atas gambar dan berakhir dalam piksel

(x, y)

$(x, y)$ . Judul

M

$M$ dipilih seperti dalam artikel ilmiah asli.

Pertama, Anda memerlukan versi dasar. Semua lapisan yang berakhir di baris paling atas hanya memiliki panjang satu piksel. Jadi, lapisan dengan energi minimum hanyalah piksel dengan energi minimum:

M (x, 0) = e (x, 0)

$M (x, 0) = e (x, 0)$

Untuk piksel di baris yang tersisa, lihat piksel di bagian atas. Karena jahitannya harus kontinu, kami hanya memperhitungkan tiga piksel yang terletak di kiri atas, atas dan kanan atas. Dari mereka kami memilih jahitan dengan energi terendah, yang berakhir di salah satu piksel ini, dan menambahkan energi dari piksel saat ini:

M (x, y) = e (x, y) + m i n b e g i n c a s e s M (x - 1, y - 1) M (x, y - 1) M (x + 1, y - 1) e n d c a s e s

$M (x, y) = e (x, y) + \ min \ begin {cases} M (x - 1, y - 1) \\ M (x, y - 1) \\ M (x + 1, y - 1) \ end {cases}$

Sebagai situasi batas, pertimbangkan kasus saat piksel saat ini berada di tepi kiri atau kanan gambar. Dalam kasus ini, kami menghilangkan

M (x - 1, y - 1)

$M (x-1, y-1)$ untuk piksel di tepi kiri atau

M (x + 1, y - 1)

$M (x + 1, y-1)$ di tepi kanan.

Akhirnya, Anda perlu mengekstrak energi dari lapisan berenergi rendah, yang mencakup seluruh ketinggian gambar. Ini berarti bahwa kita melihat garis bawah gambar dan memilih lapisan berenergi terendah yang berakhir pada salah satu piksel ini. Untuk lebar foto

W

$W$ dan tinggi

H

$H$ piksel:

m i n_{0 l e x < W} M (x, H - 1)

$\ min_ {0 \ le x <W} M (x, H - 1)$

Jadi, kami mendapat relasi berulang dengan semua properti yang diperlukan:

Relasi perulangan memiliki input bilangan bulat.
Jawaban terakhir mudah diambil dari relasi.
Rasio tergantung pada diri sendiri.

Verifikasi subtugas DAG (grafik asiklik berorientasi)

Karena setiap subtugas

M (x, y)

$M (x, y)$ sesuai dengan satu piksel dari gambar asli, grafik dependensi sangat mudah divisualisasikan. Tempatkan saja di kisi dua dimensi, seperti pada gambar asli!

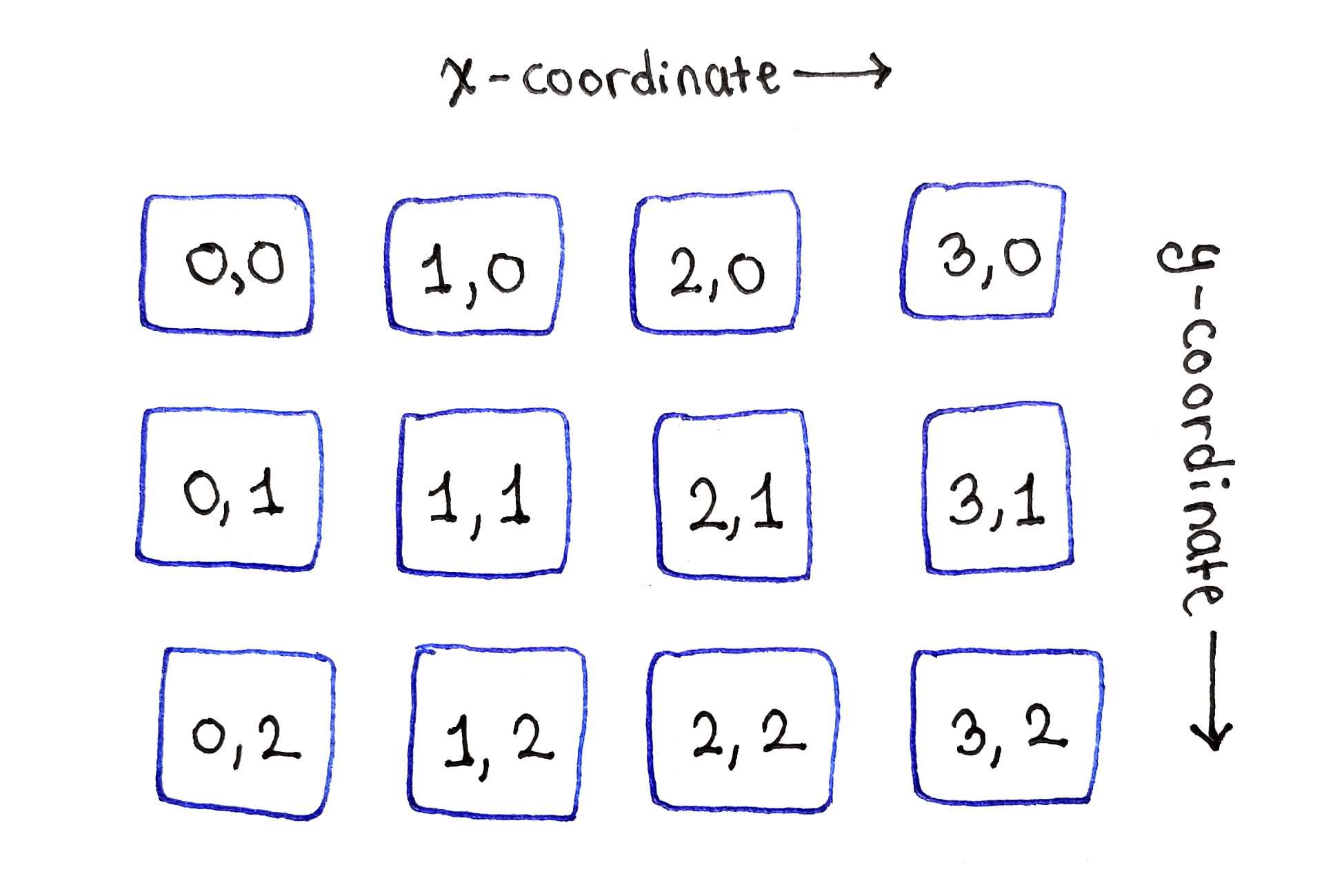Subtugas terletak di kisi dua dimensi, seperti piksel pada gambar asli

Sebagai berikut dari skenario dasar relasi perulangan, garis atas subtugas dapat diinisialisasi dengan nilai energi dari masing-masing piksel.

Baris atas tidak tergantung pada subtugas lain. Perhatikan tidak adanya panah dari baris atas sel

Di baris kedua, dependensi mulai muncul. Pertama, di sel paling kiri di baris kedua kita dihadapkan dengan situasi perbatasan. Karena tidak ada sel di sebelah kiri, sel

(1, 0)

$(1,0)$ hanya bergantung pada sel-sel yang terletak tepat di atasnya dan di kanan atas. Hal yang sama akan terjadi kemudian dengan sel paling kiri di baris ketiga.

Subtugas di tepi kiri hanya bergantung pada dua subtugas di atasnya

Di sel kedua dari baris kedua (1,1), kita melihat manifestasi paling khas dari relasi perulangan. Sel ini tergantung pada tiga sel: kiri atas, kanan atasnya dan kanan atas. Struktur dependensi ini berlaku untuk semua sel "tengah" di baris kedua dan selanjutnya.

Subtugas antara tepi kiri dan kanan bergantung pada tiga subtugas di atas

Akhirnya, sel di tepi kanan mewakili situasi garis batas kedua. Karena tidak ada lagi sel di kanan, itu hanya bergantung pada sel langsung di atas dan kiri atas.

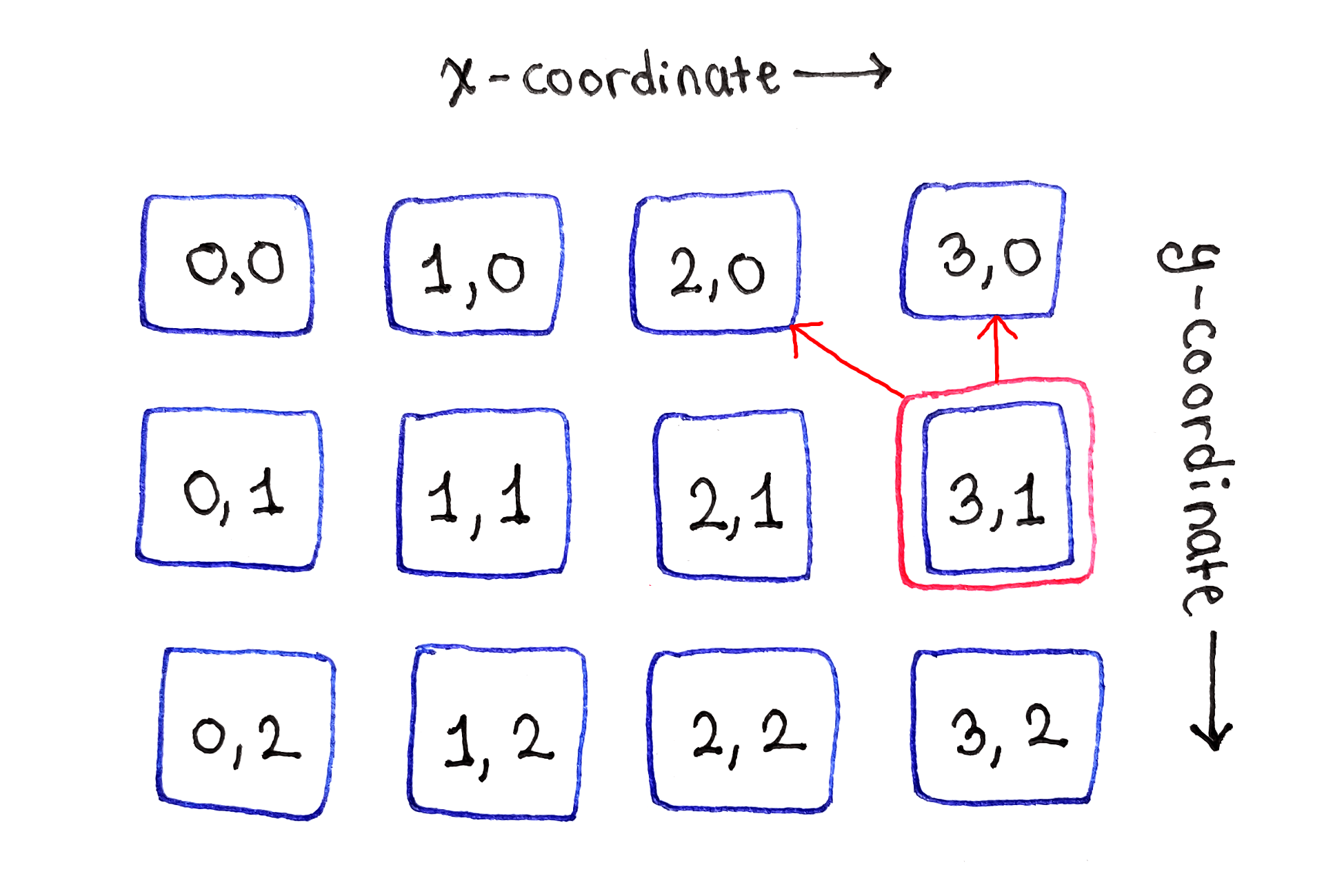Subtugas di tepi kanan hanya bergantung pada dua sel di atas

Proses ini diulangi untuk semua baris berikutnya.

Karena ada banyak panah dalam grafik dependensi, animasi ini menunjukkan dependensi untuk setiap subtugas secara bergantian

Grafik ketergantungan penuh membuat Anda takut dengan sejumlah besar panah, tetapi melihatnya satu per satu membantu membentuk pola yang eksplisit.

Implementasi dari bawah ke atas

Setelah melakukan analisis ini, kami mendapat urutan pemrosesan:

Pergi dari atas gambar ke bawah.
Setiap baris dapat bertindak dalam urutan apa pun. Pilihan alami adalah pergi dari kiri ke kanan.

Karena setiap baris hanya bergantung pada yang sebelumnya, Anda hanya perlu menyimpan dua baris data: satu untuk baris sebelumnya dan satu untuk baris saat ini. Bergerak dari kiri ke kanan, kita bahkan dapat membuang elemen individual dari baris sebelumnya saat digunakan. Namun, ini menyulitkan algoritme, karena harus mencari tahu bagian mana dari baris sebelumnya yang dapat dibuang.

Dalam kode Python berikut, input adalah daftar baris, di mana setiap baris berisi daftar angka yang mewakili energi piksel individu di baris itu. Input disebut pixel_energies , dan pixel_energies[y][x] mewakili energi piksel dalam koordinat

(x, y)

$(x, y)$ .

Mari kita mulai dengan menghitung energi lapisan-lapisan pada baris atas, cukup dengan menyalin energi pixel individu pada baris atas:

 previous_seam_energies_row = list(pixel_energies[0])

Kemudian kami menggilir melalui jalur input yang tersisa, menghitung energi jahitan untuk setiap saluran. Bagian yang paling “sulit” adalah untuk menentukan elemen mana dari garis sebelumnya untuk merujuk, karena tidak ada piksel di sebelah kiri tepi kiri atau ke kanan tepi kanan.

Pada setiap iterasi, daftar energi jahitan baru untuk garis saat ini dibuat. Pada akhir iterasi, kami mengganti data dari baris sebelumnya dengan data dari baris saat ini untuk iterasi berikutnya. Inilah cara kami membuang baris sebelumnya:

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_seam_energy = pixel_energy + \ min(previous_seam_energies_row[x_i] for x_i in x_range) seam_energies_row.append(min_seam_energy) previous_seam_energies_row = seam_energies_row

Akibatnya, previous_seam_energies_row mengandung energi jahitan untuk garis bawah. Kami menemukan nilai minimum dalam daftar ini - dan inilah jawabannya!

 min(seam_energy for seam_energy in previous_seam_energies_row)

Anda dapat menguji implementasi ini dengan membungkus kode dalam suatu fungsi, dan kemudian memanggilnya dengan array dua dimensi yang Anda buat. Input berikut telah dipilih sehingga pendekatan serakah gagal, dengan jahitan yang jelas dengan energi terendah:

 ENERGIES = [ [9, 9, 0, 9, 9], [9, 1, 9, 8, 9], [9, 9, 9, 9, 0], [9, 9, 9, 0, 9], ] print(min_seam_energy(ENERGIES))

Kompleksitas spasial dan temporal

Setiap piksel dalam gambar asli sesuai dengan satu subtugas. Untuk masing-masing subtugas, tidak ada lebih dari tiga dependensi, jadi menyelesaikannya masing-masing melibatkan jumlah pekerjaan yang konstan. Baris terakhir dipegang dua kali. Jadi untuk lebar gambar

W

$W$ dan tinggi

H

$H$ kompleksitas waktu piksel adalah

O (W \times H + W)

$O (W × H + W)$ .

Pada setiap saat, kami memiliki dua daftar: satu untuk baris sebelumnya dan satu untuk saat ini. Yang pertama

W

$W$ elemen, dan yang kedua secara bertahap meningkat menjadi

W

$W$ . Dengan demikian, kompleksitas spasialnya sama dengan

O (2 W)

$O (2W)$ itu adil

O (w)

$O (w)$ .

Perhatikan bahwa jika kita benar-benar membuang elemen data dari baris sebelumnya, kita akan mempersingkat daftar elemen dari baris sebelumnya dengan kecepatan yang sama dengan daftar baris saat ini bertambah. Dengan demikian kompleksitas spasial akan tetap ada

O (w)

$O (w)$ . Meskipun lebarnya dapat bervariasi, ini biasanya tidak terlalu penting.

Pointer Mundur Energi Rendah

Jadi, kami menemukan arti dari lapisan berenergi rendah, tetapi apa yang harus dilakukan dengan informasi ini? Sebenarnya, kita tidak peduli tentang pentingnya energi, tetapi lapisan itu sendiri! Masalahnya adalah tidak ada jalan dari pixel terakhir untuk kembali ke sisa jahitan.

Inilah yang saya lewatkan pada artikel sebelumnya, tetapi hal yang sama berlaku untuk banyak masalah pemrograman dinamis. Misalnya, jika Anda mengingat tugas perampok rumah , kami menemukan nilai maksimum untuk jumlah perampokan, tetapi bukan rumah khusus mana yang perlu dirampok untuk mendapatkan jumlah ini.

Representasi pointer belakang

Jawaban umum: simpan kembali pointer . Dalam tugas memotong lapisan, kita tidak hanya membutuhkan nilai energi dari jahitan pada setiap piksel. Anda juga perlu tahu piksel mana di baris sebelumnya yang menghasilkan energi ini. Dengan menyimpan informasi ini, kita dapat mengikuti pointer terbalik sampai ke garis atas, mendapatkan koordinat semua piksel yang membentuk sambungan dengan energi paling sedikit.

Pertama, buat kelas untuk menyimpan energi dan pointer belakang. Energi akan digunakan untuk menghitung subtugas. Karena pointer mundur menentukan piksel mana di baris sebelumnya yang memberikan energi saat ini, kita dapat membayangkannya hanya sebagai koordinat x.

 class SeamEnergyWithBackPointer(): def __init__(self, energy, x_coordinate_in_previous_row=None): self.energy = energy self.x_coordinate_in_previous_row = x_coordinate_in_previous_row

Hasil perhitungan untuk setiap subtugas bukan hanya angka, tetapi turunan dari kelas ini.

Penyimpanan Pointer Mundur

Pada akhirnya, Anda harus kembali sepanjang ketinggian gambar, mengikuti tanda-tanda terbalik untuk mengembalikan jahitan dengan energi paling sedikit. Sayangnya, ini berarti Anda harus menyimpan pointer untuk semua piksel dalam gambar, bukan hanya baris sebelumnya.

Untuk melakukan ini, kita cukup menyimpan hasil penuh dari semua subtugas, meskipun secara teknis dimungkinkan untuk menolak energi numerik dari jahitan dari baris sebelumnya. Hasilnya disimpan dalam array dua dimensi, yang terlihat sama dengan array input.

Mari kita mulai dengan baris pertama, yang hanya mengandung energi pixel individual. Karena tidak ada baris sebelumnya, semua pointer belakang tidak ada, tetapi untuk konsistensi, kami masih akan menyimpan instance SeamEnergyWithBackPointers :

 seam_energies = [] # Initialize the top row of seam energies by copying over the top row of # the pixel energies. There are no back pointers in the top row. seam_energies.append([ SeamEnergyWithBackPointer(pixel_energy) for pixel_energy in pixel_energies[0] ])

Loop utama pada dasarnya bekerja sama dengan implementasi sebelumnya, dengan perbedaan-perbedaan berikut:

Data untuk baris sebelumnya berisi contoh SeamEnergyWithBackPointer , jadi ketika menghitung nilai rasio perulangan, Anda harus mencari energi dari jahitan di dalam objek ini.
Menyimpan data untuk piksel saat ini, Anda perlu membuat instance baru SeamEnergyWithBackPointer . Di sini kita akan menyimpan energi jahitan untuk piksel saat ini, serta koordinat x dari baris sebelumnya, yang digunakan untuk menghitung energi jahitan saat ini.
Di akhir setiap baris, alih-alih membuang data dari baris sebelumnya, kami cukup menambahkan data dari baris saat ini ke seam_energies .

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_parent_x = min( x_range, key=lambda x_i: seam_energies[y - 1][x_i].energy ) min_seam_energy = SeamEnergyWithBackPointer( pixel_energy + seam_energies[y - 1][min_parent_x].energy, min_parent_x ) seam_energies_row.append(min_seam_energy) seam_energies.append(seam_energies_row)

Ikuti tanda-tandanya

Sekarang seluruh tabel subtugas diisi dan kita dapat mengembalikan lapisan dengan energi paling sedikit. Kita mulai dengan mencari koordinat x di garis bawah, yang sesuai dengan sambungan dengan energi paling sedikit:

 # Find the x coordinate with minimal seam energy in the bottom row. min_seam_end_x = min( range(len(seam_energies[-1])), key=lambda x: seam_energies[-1][x].energy )

Sekarang pergi dari bagian bawah gambar ke atas, berubah

y

$y$ dari len(seam_energies) - 1 hingga nol. Di setiap iterasi, tambahkan pasangan saat ini

(x, y)

$(x, y)$ ke daftar yang mewakili jahitan kami, dan kemudian atur nilainya

x

$x$ untuk objek yang SeamEnergyWithBackPointer di baris saat ini.

 # Follow the back pointers to form a list of coordinates that form the # lowest-energy seam. seam = [] seam_point_x = min_seam_end_x for y in range(len(seam_energies) - 1, -1, -1): seam.append((seam_point_x, y)) seam_point_x = \ seam_energies[y][seam_point_x].x_coordinate_in_previous_row seam.reverse()

Jadi jahitan dibangun ke atas, daftar kemudian dapat dibaca dalam urutan terbalik, jika Anda memerlukan koordinat dari atas ke bawah.

Kompleksitas spasial dan temporal

Kompleksitas waktu mirip dengan yang sebelumnya, karena kita masih perlu memproses setiap piksel satu kali. Setelah melihat baris terakhir dan menemukan sambungan dengan energi paling sedikit, kami kemudian naik seluruh ketinggian gambar untuk memulihkan sambungan. Jadi untuk gambar

W \times H

$W × H$ kompleksitas waktu sama dengan

O (W \times H + W + H)

$O (W × H + W + H)$ .

Mengenai volume, kami masih menyimpan jumlah data yang konstan untuk setiap subtugas, tetapi sekarang kami tidak membuang data apa pun. Jadi kami menggunakan volume

O (W \times H)

$O (W × H)$ .

Penghapusan jahitan energi rendah

Segera setelah sambungan vertikal dengan energi terendah ditemukan, kita cukup menyalin piksel dari gambar asli ke gambar baru. Setiap baris gambar baru berisi semua piksel dari garis yang sesuai dari gambar asli, dengan pengecualian piksel dari lapisan dengan energi terendah. Karena kami menghapus satu piksel di setiap baris, mulai dari gambar

W \times H

$W × H$ lalu kita dapatkan gambarnya

(W - 1) \times H

$(W - 1) × H$ .

Kita dapat mengulangi proses ini dengan menceritakan fungsi energi pada gambar baru dan menemukan lapisan energi terendah di atasnya. Tampaknya tergoda untuk menemukan lebih dari satu jahitan berenergi rendah pada gambar asli, dan kemudian menghapusnya sekaligus. Masalahnya adalah bahwa kedua jahitan tersebut dapat bersilangan. Ketika yang pertama dihapus, yang kedua akan menjadi tidak valid karena satu atau lebih piksel hilang darinya.

Animasi proses pelepasan jahitan. Lebih baik tonton di layar penuh untuk tampilan jahitan yang lebih jelas

Setiap bingkai video adalah gambar pada setiap iterasi dengan visualisasi lapisan yang dilapis dengan energi paling sedikit.

Contoh lain

Artikel ini memiliki banyak penjelasan terperinci, jadi mari kita akhiri dengan serangkaian foto yang indah! Foto berikut menunjukkan formasi batuan di Taman Nasional Arches:

Formasi batu dengan lubang di Taman Nasional Arches. Foto: Mike Goad di Flickr

Fungsi energi untuk gambar ini:

Energi setiap piksel dalam foto: semakin terang - semakin tinggi. Perhatikan energi tinggi di sekitar tepi lubang.

Sebagai hasil dari perhitungan, diperoleh jahitan dengan energi terendah. Perhatikan bahwa ia melewati batu di sebelah kanan, masuk langsung ke formasi batuan di mana bagian yang diterangi di atas batu cocok dengan warna langit. Mungkin Anda harus memilih fungsi energi yang lebih baik!

Jahitan berenergi terendah yang ditemukan dalam gambar ditunjukkan dengan garis merah lima piksel lebar untuk visibilitas, meskipun sebenarnya jahitannya hanya satu piksel lebar.

Akhirnya, gambar lengkungan setelah mengubah ukuran:

Lengkungan setelah kompresi pada 1024 piksel

Hasilnya jelas tidak sempurna: banyak sisi gunung dari gambar asli terdistorsi. Salah satu perbaikan mungkin adalah implementasi dari salah satu fungsi energi lainnya yang tercantum dalam artikel ilmiah.

Meskipun pemrograman dinamis biasanya dibahas dalam teori, ini adalah metode praktis yang berguna untuk menyelesaikan masalah yang kompleks. Pada artikel ini, kami memeriksa salah satu aplikasi pemrograman dinamis: mengubah ukuran gambar agar sesuai dengan konten dengan memotong jahitan.

Kami menerapkan prinsip yang sama untuk membagi masalah ke dalam subtugas yang lebih kecil, menganalisis dependensi antara subtugas ini, dan kemudian memecahkan subtugas dalam urutan yang meminimalkan kompleksitas spasial dan temporal dari algoritma. Selain itu, kami mempelajari penggunaan pointer terbalik untuk tidak hanya menemukan nilai energi untuk jahitan yang optimal, tetapi juga untuk menentukan koordinat setiap piksel yang membentuk nilai ini. Kemudian kami menerapkan bagian-bagian ini pada masalah nyata, yang membutuhkan beberapa pra dan pasca pemrosesan untuk penggunaan algoritma pemrograman dinamis yang benar-benar efektif.

Pemrograman dinamis di dunia nyata: pemotongan jahitan

Ubah ukuran gambar berdasarkan konten

Definisi Energi Gambar

Cari lapisan berenergi rendah dengan pemrograman dinamis

Kami memecah masalah menjadi subtugas

Definisi relasi perulangan

Verifikasi subtugas DAG (grafik asiklik berorientasi)

Implementasi dari bawah ke atas

Kompleksitas spasial dan temporal

Pointer Mundur Energi Rendah

Representasi pointer belakang

Penyimpanan Pointer Mundur

Ikuti tanda-tandanya

Kompleksitas spasial dan temporal

Penghapusan jahitan energi rendah

Contoh lain

More articles: