Di sekolah, ketika kami memecahkan persamaan atau rumus yang dianggap, kami mencoba menguranginya beberapa kali, misalnya, Z = X - (Y + X) dikurangi menjadi Z = -Y . Dalam kompiler modern, ini adalah subset dari apa yang disebut optimisasi lubang, di mana, secara kasar, seperangkat pola yang kita kurangi ekspresi, ganti instruksi dengan yang lebih cepat untuk prosesor tertentu, dll. Dalam artikel ini, saya telah mengumpulkan kumpulan optimisasi yang ditemukan di sumber LLVM, GCC, dan .NET Core (CoreCLR).
Mari kita mulai dengan contoh sederhana:
X * 1 => X -X * -Y => X * Y -(X - Y) => Y - XX * Z - Y * Z => Z * (X - Y)
periksa contoh terakhir di C ++ dan di C #:
int Test(int x, int y, int z) { return x * z - y * z;
dan lihat assembler dari Dentang (LLVM), GCC, MSVC, dan .NET Core:

Ketiga kompiler C ++ (GCC, Dentang dan MSVC) mengurangi satu multiplikasi (kita hanya melihat satu instruksi imul ). C # tidak melakukan ini dengan RyuJIT, tetapi jangan buru-buru memarahinya karena itu, hanya saja kelas optimisasi ini tersedia dalam komposisi terbatas di sana. Untuk membuat Anda mengerti, implementasi seluruh transformasi InstCombine di LLVM membutuhkan lebih dari 30k baris kode (+ 20k baris pada DAGCombiner.cpp), terlebih lagi, transformasi ini sering menyebabkan kompilasi yang panjang. Omong-omong, situs yang bertanggung jawab untuk optimasi ini ada di sana. GCC memiliki DSL khusus yang menjelaskan lubang optimasi, di sini adalah cuplikan ).
Saya memutuskan, demi artikel ini, untuk mencoba mengimplementasikan pengoptimalan ini di C # JIT (tahan bir saya):
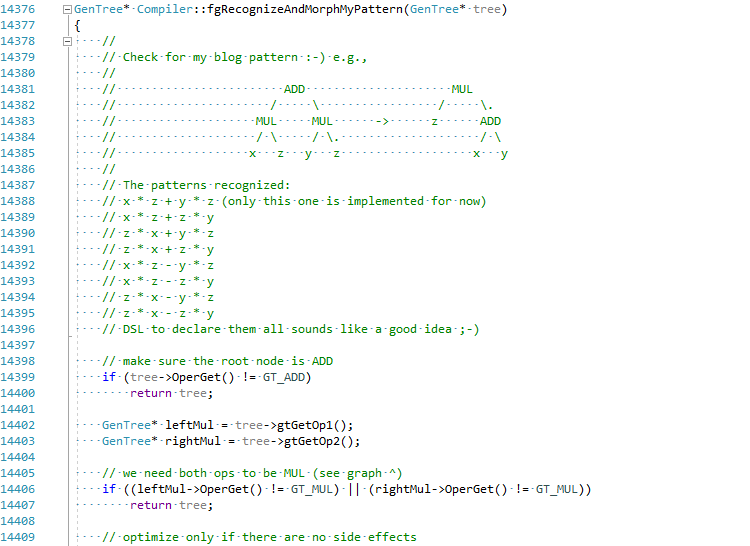
Komit penuh dapat dilihat di sini EgorBo / coreclr . Mari kita periksa peningkatan saya sekarang (di Visual Studio 2019 + Disasmo:
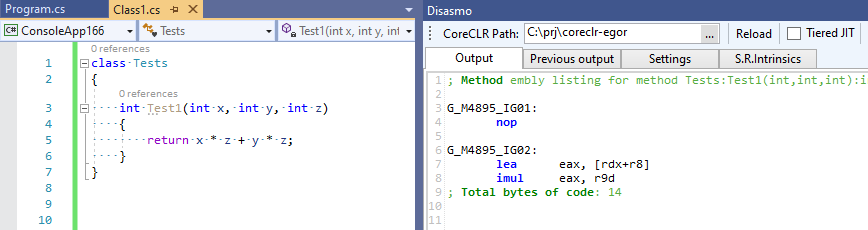
Itu berhasil! lea + imul bukannya imul , imul dan add .
Mari kita kembali ke C ++ dan melacak pengoptimalan ini di Dentang. Untuk melakukan ini, mintalah dentang untuk memberikan kami LLVM IR awal melalui -emit-llvm -g0 , dan kemudian berikan kepada LLVM ke pengoptimal, menggunakan parameter -O2 -print-before-all -print-after-all untuk menangkap momen transformasi yang tepat menghapus perkalian dari set -O2 (semua ini dapat dilihat pada sumber daya yang luar biasa godbolt.org ):
; *** IR Dump Before Combine redundant instructions *** define dso_local i32 @_Z5Case1iii(i32, i32, i32) { %4 = mul nsw i32 %0, %2 %5 = mul nsw i32 %1, %2 %6 = sub nsw i32 %4, %5 ret i32 %6 } ; *** IR Dump After Combine redundant instructions *** define dso_local i32 @_Z5Case1iii(i32, i32, i32) { %4 = sub i32 %0, %1 %5 = mul i32 %4, %2 ret i32 %5 }
Anda juga dapat bersenang-senang di godbolt dengan alat LLVM - opt (pengoptimal) dan llc (untuk mengkompilasi LLVM IR ke asm):

Kembali ke contoh. Saya menemukan contoh yang sangat bagus di GCC.
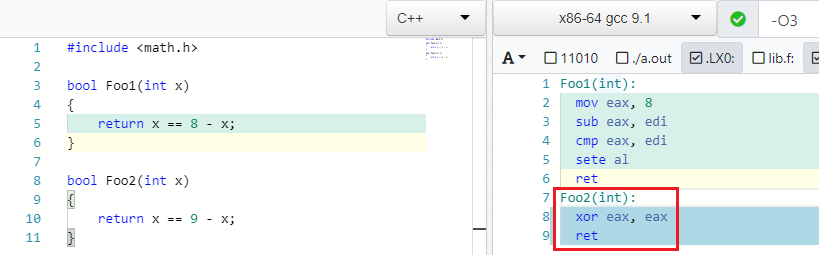
X == C - X => false if C is odd
Dan memang benar: jika 4 == 8 - 4 . Tetapi jika alih-alih 8 Anda menulis yang aneh, maka Anda tidak dapat menemukan X sedemikian rupa sehingga kesetaraan terpenuhi:
IEEE754 Menyerang Kembali
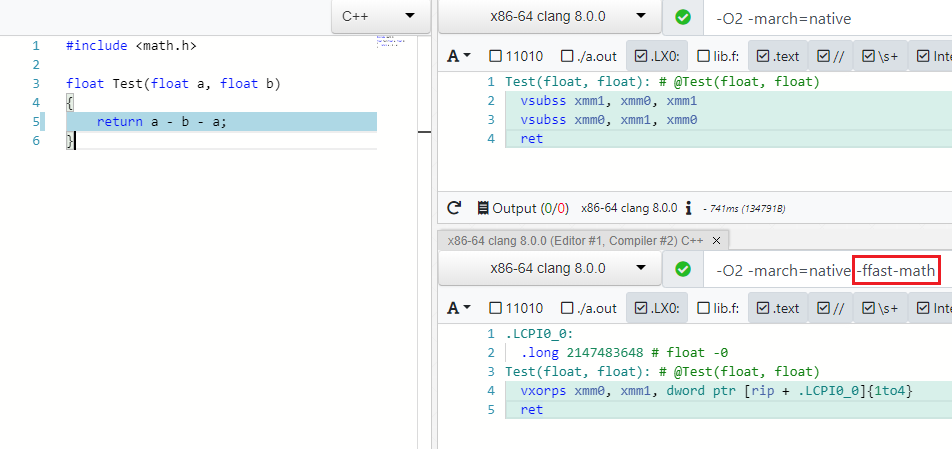
Banyak optimasi bekerja untuk tipe data yang berbeda, misalnya, byte , int , unsigned , float , double . Dengan yang terakhir, semuanya tidak begitu sederhana dan optimisasi ditangani oleh spesifikasi IEEE754, yang akan menjadi gila jika Anda mengurangi A - B - A ke -B atau (A * B) * C mengatur ulang ke A * (B * C) t. untuk. operasi tidak asosiatif. Tetapi ada mode khusus dalam kompiler modern yang memungkinkan Anda untuk mengabaikan nilai spec dan batas (NaN, + -Inf, + -0.0) dalam kasus seperti itu dan melakukan optimasi dengan aman - ini adalah Matematika Cepat (permintaan PR saya untuk menambahkan mode seperti itu ke C # dapat ditemukan di sini )
Seperti yang Anda lihat di -ffast-math tidak ada lagi dua vsubss :
Selain ekspresi, pengoptimal juga memperhitungkan juggling dengan fungsi matematika dari math.h , misalnya, produk moduli angka X sama dengan produk angka X:
abs(X) * abs(X) => X * X
Akar kuadrat selalu positif:
sqrt(X) < Y => false, if Y is negative. sqrt(X) < 0 => false
Mengapa menghitung root, jika mungkin pada tahap kompilasi untuk menghitung kuadrat konstanta di sebelah kanan?:
sqrt(X) > C => X > C * C

Lebih banyak operasi root:
sqrt(X) == sqrt(Y) => X == Y sqrt(X) * sqrt(X) => X sqrt(X) * sqrt(Y) => sqrt(X * Y) logN(sqrt(X)) => 0.5*logN(X)
Beberapa matematika sekolah lagi:
expN(X) * expN(Y) -> expN(X + Y)
Dan pengoptimalan favorit saya:
sin(X) / cos(X) => tan(X)

Banyak operasi bit dan boolean yang membosankan:
((a ^ b) | a) -> (a | b) (a & ~b) | (a ^ b) --> a ^ b ((a ^ b) | a) -> (a | b) (X & ~Y) |^+ (~X & Y) -> X ^ Y A - (A & B) into ~B & A X <= Y - 1 equals to X < Y A < B || A >= B -> true ... !
Optimalisasi tingkat rendah
Ada serangkaian optimisasi yang pada pandangan pertama tidak masuk akal matematikawan, tetapi lebih ramah terhadap besi.
X / 2 => X * 0.5
ganti pembagian dengan perkalian:

Pengoperasian multiplikasi armada biasanya memiliki karakteristik latensi / throughput yang lebih baik daripada divisi. Misalnya, berikut adalah opsi untuk Intel Haswell:

Dalam mode non-cepat-matematika, itu hanya dapat digunakan jika konstanta adalah kekuatan dua.
Ngomong-ngomong, saya baru-baru ini mencoba menambahkan optimasi seperti itu di C #. Yaitu jika, misalnya, Anda perlu membuka file dengan model 3D dan mengurangi semua koordinat sebanyak 10 kali, maka * 0,1 akan menangani ini 20-100% lebih cepat, yang bisa jadi signifikan.
Alasan yang sama untuk:
X * 2 => X + X
Membandingkan dengan nol ( test ) lebih baik daripada membandingkan dengan satuan ( cmp ) - PR saya untuk detailnya adalah dotnet / coreclr # 25458 :
X >= 1 => X > 0 X < 1 => X <= 0 X <= -1 => X >= 0 X > -1 => X >= 0
Dan bagaimana Anda suka ini:
pow(X, 0.5) => sqrt(x) pow(X, 0.25) => sqrt(sqrt(X)) pow(X, 2) => X * X ; 1 mul pow(X, 3) => X * X * X ; 2 mul

Bagaimana menurut Anda, berapa banyak operasi multiplikasi yang Anda perlukan untuk menghitung mod(X, 4) atau X * X * X * X ?
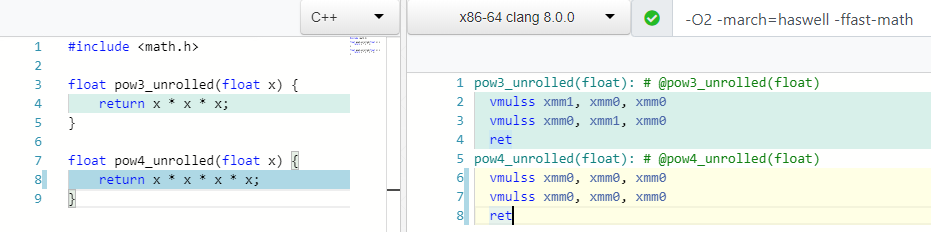
Dua! Serta untuk menghitung derajat ke-3, dan dalam kasus 4 kita hanya menggunakan satu register xmm0 .
Banyak prosesor mendukung instruksi khusus (FMA), yang memungkinkan Anda untuk melakukan perkalian dan penambahan pada satu waktu, sambil menjaga akurasi selama perkalian:
X * Y + Z => fmadd(X, Y, Z)

Dua contoh favorit saya melipat beberapa algoritma menjadi satu instruksi (jika prosesor mendukungnya):
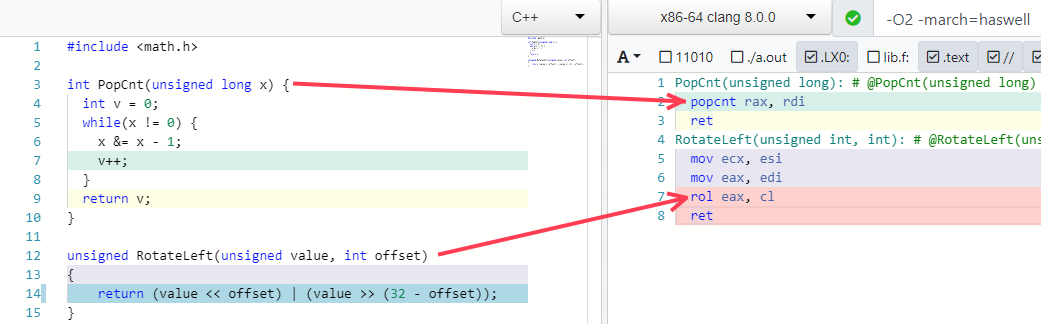
Jebakan Optimasi
Saya pikir semua orang mengerti bahwa Anda tidak bisa terburu-buru dan mengurangi ekspresi karena tiga alasan:
- Anda dapat memecahkan kode pada beberapa nilai batas, overflow, efek samping tersembunyi, dll ... Bugzilla LLVM berisi banyak bug InstCombine.
- Idealnya, optimasi harus bekerja bersama dalam urutan tertentu.
- Ekspresi atau bagiannya yang ingin Anda kurangi dapat digunakan di tempat lain dan pengurangannya akan menyebabkan penurunan kinerja.
Mari kita lihat contoh paragraf terakhir (lihat di artikel Future Directions for Optimizing Compiler ).
Bayangkan kita memiliki kode ini:
int Foo1(int a, int b) { int na = -a; int nb = -b; return na + nb; }
kita perlu melakukan tiga operasi: 0 - a , 0 - b , dan na + nb . Tetapi pengoptimal bagi kita mengurangi ini menjadi dua - return -(a + b); :
define dso_local i32 @_Z4Foo1ii(i32, i32) { %3 = add i32 %0, %1 ; a + b %4 = sub i32 0, %3 ; 0 - %3 ret i32 %4 }
Sekarang bayangkan bahwa kita perlu menulis nilai antara na dan nb ke variabel global:
int x, y; int Foo2(int a, int b) { int na = -a; int nb = -b; x = na; y = nb; return na + nb; }
Pengoptimal masih menemukan pola ini dan menghapus operasi 0 - a dan 0 - b tidak perlu (dari sudut pandangnya), tetapi ternyata itu diperlukan! kami menulis hasil dari operasi "yang tidak perlu" ini ke dalam variabel global! Ini mengarah ke kode ini:
define dso_local i32 @_Z4Foo2ii(i32, i32) { %3 = sub nsw i32 0, %0 ; 0 - a %4 = sub nsw i32 0, %1 ; 0 - b store i32 %3, i32* @x, align 4, !tbaa !2 store i32 %4, i32* @y, align 4, !tbaa !2 %5 = add i32 %0, %1 ; a + b %6 = sub i32 0, %5 ; 0 - %5 ret i32 %6 }
Empat operasi matematika, bukan tiga! Pengoptimal kami gagal dan tidak yakin bahwa ekspresi perantara yang ia optimalkan masih diperlukan oleh seseorang. Sekarang mari kita lihat output C # RuyJIT, di mana tidak ada optimasi pintar seperti itu:
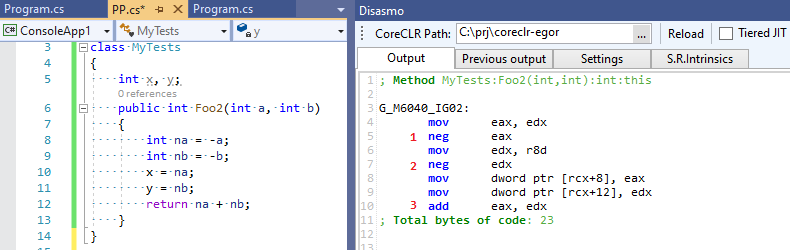
Tiga operasi bukannya empat - C # ternyata lebih cepat daripada C ++ :-)!
Apakah optimasi seperti itu diperlukan?
Anda tidak pernah tahu bagaimana kode akan terlihat setelah kompiler menyatukan semua yang dapat dan dilakukannya pelipatan konstan, penyalinan salinan, CSE, dll. - gambar yang sama sekali berbeda akan terbuka untuknya. LLVM IR dan .NET IL tidak terikat dengan bahasa pemrograman tertentu, dan Anda tidak dapat memastikan bahwa PL tertentu / baru dapat secara efektif menerjemahkan dirinya ke dalam IR. Nah, mengapa membicarakannya jika Anda dapat menguji kinerja InstCombine hidup dan mati pada aplikasi tertentu ;-). Tidak mungkin ini akan menjadi perbedaan yang mengesankan, tetapi siapa yang tahu.
Bagaimana dengan C #?
Seperti yang saya katakan, optimisasi ekspresi yang kami periksa kemungkinan besar tidak ada di C #. Tetapi ketika saya mengatakan C # Maksud saya runtime paling populer adalah CoreCLR dan RyuJIT. Tapi selain CoreCLR ada runtime lain, termasuk yang menggunakan LLVM sebagai backend: Mono (lihat tweet saya), Unity Burst, IL2CPP (via dentang) dan LILLC - di sini Anda dapat dengan aman membandingkan hasil C ++ dengan dentang. Orang-orang dari Unity bahkan menulis ulang kode C ++ internal di C # tanpa kehilangan kinerja, buktikan !
Berikut adalah beberapa lubang optimasi yang dapat ditemukan di file morph.cpp dalam kode sumber morph.cpp dari komentar (jelas ada sedikit lebih banyak):
*(&X) => X X % 1 => 0 X / 1 => X X % Y => X - (X / Y) * Y X ^ -1 => ~x X >= 1 => X > 0 X < 1 => X <= 0 X + 1 == C2 => X == C2 - C1 ((X + C1) + C2) => (X + (C1 + C2)) ((X + C1) + (Y + C2)) => ((X + Y) + (C1 + C2))
Beberapa lagi dapat ditemukan di lowering.cpp (level rendah), tetapi secara umum RyuJIT jelas kehilangan di sini karena kompiler C ++. RyuJIT memiliki prioritas yang sedikit berbeda - sebelum munculnya Tiering Compilation, ia perlu memberikan kecepatan kompilasi yang dapat diterima, yang ia lakukan dengan sangat baik tidak seperti kompiler C ++ (ingat tentang 30-baris InstCombine yang lulus dalam LLVM dan membaca posting yang menarik secara umum " Modern "C ++ Ratapan ) dan itu jauh lebih berguna untuk mengembangkan optimasi di bidang devirtualisasi panggilan, penghapusan tinju dan alokasi (Alokasi Objek Tumpukan yang sama) - semua ini, jelas, jauh lebih penting daripada meminimalkan pembagian sinus oleh cosinus menjadi tangen.
Mungkin dengan munculnya Tiering Compilation, seiring waktu akan ada banyak optimasi baru yang tidak penting untuk waktu kompilasi untuk tier1 atau bahkan tier2. Mungkin bahkan dengan Add-in API dan DSL Anda - Anda baru saja membaca artikel ini, di dalamnya Prathamesh Kulkarni menambahkan pengoptimalan ekspresi dalam GCC hanya dalam beberapa jalur DSL:
(simplify (plus (mult (SIN @0) (SIN @0)) (mult (COS @0) (COS @0))) (if (flag_unsafe_math_optimizations)1. { build_one_cst (TREE_TYPE (@0))
untuk ungkapan ini dari buku teks matematika ;-):
cos^2(X) + sin^2(X) equals to 1
Tautan yang bermanfaat
- "Arah Masa Depan untuk Mengoptimalkan Kompiler" , Nuno P. Lopes dan John Regehr
- "Bagaimana LLVM Mengoptimalkan Fungsi" , John Regehr
- "Kecerdasan mengejutkan kompiler modern" , Daniel Lemire
- "Menambahkan optimalisasi lubang intip ke GCC" , Prathamesh Kulkarni
- "1. C ++, C # dan Unity" , Lucas Meijer
- "Modern" C ++ Ratapan " , Aras Pranckevičius
- "Optimalisasi Optimal Lubang Pengamatan dengan Hidup" , Nuno P. Lopes, David Menendez, Santosh Nagarakatte dan John Regehr