Geekly articles weekly

Model matematika teleskop radio super panjang

Pendahuluan


Salah satu teleskop radio pertama yang dibangun oleh American Grotto Reber pada tahun 1937. Teleskop radio adalah cermin timah dengan diameter 9,5 m yang dipasang pada bingkai kayu:



Pada 1944, Reber telah menyusun peta pertama distribusi gelombang radio ruang angkasa di wilayah Bima Sakti.

Perkembangan astronomi radio memerlukan sejumlah penemuan: pada tahun 1946, emisi radio dari rasi Cygnus ditemukan, pada tahun 1951 - radiasi ekstragalaktik, pada tahun 1963 - quasar, dan pada tahun 1965 mengandalkan radiasi latar pada panjang gelombang 7,5 cm.

Pada tahun 1963, teleskop radio 300 meter yang unik dibangun di Arecibo (Puerto Rico). Ini adalah mangkuk tak bergerak dengan irradiator bergerak, dibangun di celah alami dari medan.



Teleskop radio tunggal memiliki resolusi sudut kecil, yang ditentukan oleh rumus:
 T h e t a = f r a c l a m b d a d  
dimana  l a m b d a - panjang gelombang d - diameter teleskop radio.

Jelas, untuk meningkatkan resolusi, perlu untuk meningkatkan diameter antena, yang secara fisik merupakan tugas yang sulit. Itu mungkin untuk menyelesaikannya dengan munculnya interferometer radio.



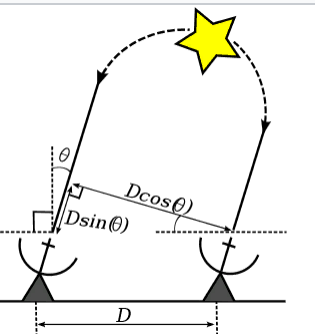
Bagian depan gelombang elektromagnetik yang dipancarkan oleh bintang yang jauh di dekat Bumi dapat dianggap datar. Dalam kasus interferometer paling sederhana, yang terdiri dari dua antena, perbedaan dalam jalur sinar yang tiba di dua antena ini akan sama dengan:
 D e l t a = D c d o t s i n ( T h e t a )   ,
dimana:  D e l t a - perbedaan jalur sinar; D - jarak antar antena;  T h e t a - sudut antara arah kedatangan sinar dan normal ke garis di mana antena berada.

Di  T h e t a = 0 gelombang yang tiba di kedua antena dirangkum secara bertahap. Dalam antiphase, gelombang akan muncul untuk pertama kalinya dengan:

 Delta= frac lambda2, Theta=arcsin frac lambda2D ,
dimana:  lambda - panjang gelombang.

Maksimum berikutnya adalah pada  Delta= lambda, minimum pada  Delta= frac3 lambda2 dll. Pola radiasi multi-kelopak (DN) diperoleh, lebar lobus utama di mana pada  lambda<<D sama dengan  lambda/D . Lebar lobus utama menentukan resolusi sudut maksimum interferometer radio, kira-kira sama dengan lebar lobus.

Ultra-long base radio interferometry (VLBI) adalah jenis interferometri yang digunakan dalam astronomi radio di mana elemen-elemen penerima interferometer (teleskop) terletak tidak lebih dekat daripada pada jarak kontinental satu sama lain.

Metode VLBI memungkinkan Anda untuk menggabungkan pengamatan yang dilakukan oleh beberapa teleskop, dan dengan demikian mensimulasikan teleskop yang dimensinya sama dengan jarak maksimum antara teleskop asli. Resolusi sudut VLBI adalah puluhan ribu kali lebih besar daripada resolusi instrumen optik terbaik.

Keadaan jaringan VLBI saat ini


Saat ini, beberapa jaringan VLBI mendengarkan ruang:

  • European –EVN (European VLBI Network), terdiri dari lebih dari 20 teleskop radio;
  • Amerika –VLBA (Very Long Baseline Array), yang mencakup sepuluh teleskop dengan diameter masing-masing 25 meter;
  • Jepang - JVN (Jaringan VLBI Jepang) terdiri dari sepuluh antena yang berlokasi di Jepang, termasuk empat antena astrometri (proyek VERA - VLBI Eksplorasi Radio Astrometri);
  • Australian - LBA (Long Baseline Array);
  • Cina - CVN (Jaringan VLBI Cina), terdiri dari empat antena;
  • Korea Selatan - KVN (Jaringan VLBI Korea), yang mencakup tiga teleskop radio 21 meter;
  • Yang Rusia didasarkan pada kompleks interferometrik radio permanen Kvazar-KVO dengan teleskop radio dengan diameter 32 m, dilengkapi dengan cryoradiometer yang sangat sensitif dalam kisaran panjang gelombang dari 1,35 cm hingga 21 cm. Panjang pangkalan - diameter efektif "cermin" yang disintesis - sekitar 4400 km ke arah timur-barat (lihat gambar).



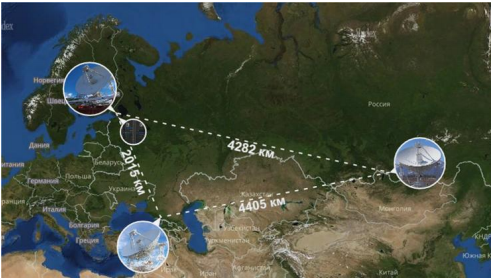
Di kompleks VLBI "Kvazar-KVO", standar hidrogen digunakan sebagai sumber frekuensi referensi untuk semua transformasi frekuensi, yang menggunakan transisi antara tingkat struktur hyperfine dari keadaan dasar atom hidrogen dengan frekuensi 1420,405 MHz, sesuai dengan 21 cm dalam astronomi radio.

Tugas diselesaikan melalui VLBI


  • Astrofisika Gambar-gambar radio dari benda-benda luar angkasa alami (quasar dan benda-benda lainnya) sedang dibangun dengan resolusi sepersepuluh dan ratusan mas (milidetik dari busur).
  • Studi astrometri. Pembangunan sistem koordinat waktu. Objek penelitian adalah sumber radio dengan ukuran sudut yang sangat kecil, termasuk sumber radio quasistellar dan nukleus galaksi radio, yang, karena jaraknya yang sangat jauh, merupakan objek yang hampir ideal untuk menciptakan jaringan yang mendukung benda-benda diam.
  • Penelitian tentang mekanika langit dan dinamika tata surya, navigasi ruang angkasa. Pemasangan suar di permukaan planet dan melacak suar stasiun otomatis antarplanet memungkinkan untuk menggunakan metode VLBI untuk mempelajari parameter seperti gerakan orbital planet, arah sumbu rotasi dan presesi mereka, dinamika sistem planet-satelit. Untuk Bulan, masalah yang sangat penting dalam menentukan persalinan fisik dan menentukan dinamika sistem Bulan-Bumi juga sedang diselesaikan.

Navigasi di ruang angkasa menggunakan VLBI


  • Memantau pergerakan astronot di permukaan bulan pada tahun 1971. Mereka bergerak dengan bantuan penjelajah bulan Rover. Keakuratan menentukan posisinya relatif terhadap modul bulan mencapai 20 cm dan tergantung terutama pada librasi bulan (Librasi - osilasi seperti pendulum periodik bulan relatif terhadap pusat massanya);
  • Dukungan navigasi untuk pengiriman dan pelepasan probe aerostat dari kendaraan terbang ke atmosfer Venus (proyek VEGA). Jarak ke Venus lebih dari 100 juta km, daya pemancar hanya 1 Watt. Peluncuran VEGA-1/2 berlangsung pada bulan Desember 1984. Balon dijatuhkan ke atmosfer Venus pada tanggal 11 dan 15 Juni 1985. Pengamatan dilakukan selama 46 jam.

Diagram struktural dari jaringan VLBI yang disederhanakan


Berdasarkan jaringan VLBI nyata, menggunakan perangkat lunak Python, kami memodelkan sistem VLBI sederhana dalam bentuk model terpisah untuk setiap unit atau proses. Set model ini akan cukup untuk mengamati proses dasar. Diagram struktural dari jaringan VLBI yang disederhanakan disajikan pada gambar:



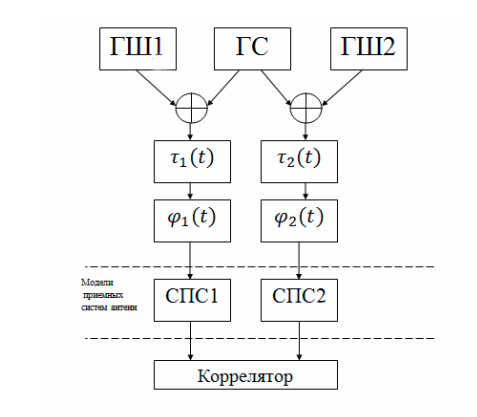
Sistem ini mencakup komponen-komponen berikut:

  • generator sinyal termodulasi fase (HS);
  • generator derau (GSh1, GSh2). Sistem ini memiliki dua teleskop radio (antena penerima) yang memiliki noise sendiri. Selain itu, ada suara-suara atmosfer dan sumber-sumber alami dan buatan dari emisi radio;
  • unit waktu tunda yang mensimulasikan penundaan waktu yang bervariasi secara linear karena rotasi Bumi;
  • fase shifter mensimulasikan efek Doppler;
  • sistem konversi sinyal (SPS), yang terdiri dari osilator lokal, untuk mentransfer sinyal ke bawah dalam frekuensi, dan filter band-pass;
  • Korelasi FX.

Rangkaian korelator ditunjukkan pada gambar berikut:



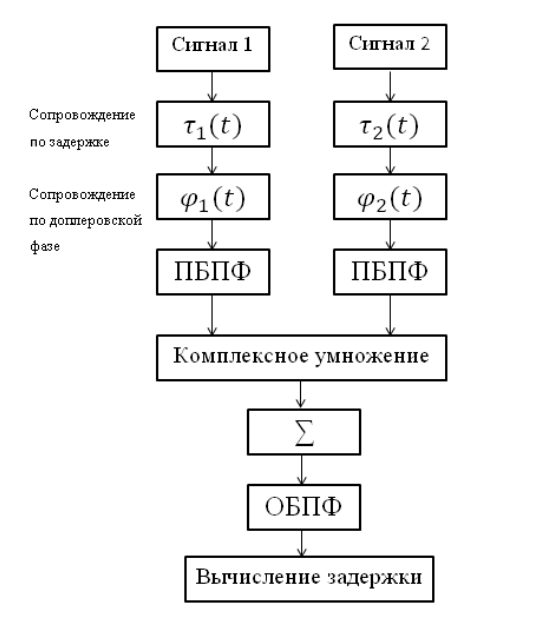
Rangkaian korelasi yang diberikan, yang meliputi blok-blok berikut:

  • Transformasi Fourier cepat cepat (PBPF) dan Transformasi Fourier terbalik (OBPF);
  • mengkompensasi keterlambatan yang diperkenalkan sebelumnya;
  • mengkompensasi efek Doppler;
  • perkalian kompleks dua spektrum;
  • menjumlahkan implementasi yang terakumulasi.

Model Sinyal Navigasi


Yang paling nyaman untuk pengukuran VLBI adalah sinyal navigasi pesawat ruang angkasa dari sistem navigasi satelit, seperti GPS dan GLONASS. Sejumlah persyaratan diberlakukan pada sinyal navigasi:

  • memungkinkan Anda untuk mendefinisikan pseudorange dengan baik;
  • mengirimkan informasi tentang posisi sistem navigasi;
  • dapat dibedakan dari sinyal NS lainnya;
  • Jangan mengganggu sistem radio lain;
  • tidak memerlukan peralatan kompleks untuk menerima dan mengirim.

Sampai batas tertentu mereka puas dengan sinyal dengan modulasi fase biner (dua posisi) - BPSK (kunci pergeseran fase biner), yang dalam literatur Rusia dilambangkan sebagai FM-2. Modulasi ini mengubah fase osilasi pembawa oleh π, yang dapat direpresentasikan sebagai:

S(t)=A cdotG(t) cdotcos(2 pift),

di mana G (t) adalah fungsi modulasi.

Untuk mengimplementasikan modulasi fase, dua generator dapat digunakan, yang masing-masing membentuk frekuensi yang sama, tetapi dengan fase awal yang berbeda. Fungsi modulasi memungkinkan Anda untuk memperluas spektrum sinyal dan secara akurat mengukur pseudorange (jarak antara satelit dan penerima, dihitung dari waktu propagasi sinyal tanpa koreksi untuk perbedaan antara jam dari satelit dan penerima).

Berikut ini adalah daftar yang menjelaskan prinsip-prinsip dasar BPSK:

Daftar
from scipy import* from pylab import* import numpy as np import scaleogram as scg f = 2; #f  fs = 100; #    t = arange(0,1,1/fs) #    1 / fs #      BPSK p1 = 0; p2 = pi; #     N =12#     #   bit_stream=np.random.random_integers(0, 1, N+1) #   time =[]; digital_signal =[]; PSK =[]; carrier_signal =[]; #  for ii in arange(1,N+1,1): #   if bit_stream [ii] == 0: bit = [0 for w in arange(1,len(t)+1,1)]; else: bit = [1 for w in arange(1,len(t)+1,1)]; digital_signal=hstack([digital_signal,bit ]) #  BPSK if bit_stream [ii] == 0: bit = sin (2*pi*f*t+p1); else: bit = sin (2*pi*f*t+p2); PSK=hstack([PSK,bit]) #   carrier = sin (2*f*t*pi); carrier_signal = hstack([carrier_signal,carrier]) ; time = hstack([time ,t]); t=t+1 suptitle("    (BPSK)") subplot (3,1,1); plot(time,digital_signal,'r'); grid(); subplot (3,1,2); plot (time,PSK); grid(); subplot (3,1,3); plot (time,carrier_signal); grid() show() figure() title("     (BPSK)") n = len(PSK) k = np.arange(n) T = n/fs frq = k/T frq = frq[np.arange(int(n/2))] Y = fft(PSK)/n Y = Y[range(n //2)] / max(Y[range(n // 2)]) plot(frq[75:150], abs(Y)[75:150], 'b')#    grid() #   PSK  scales = scg.periods2scales( arange(1, 40)) ax2 = scg.cws(PSK, scales=scales, figsize=(6.9,2.9)); show()


Kami mendapatkan:







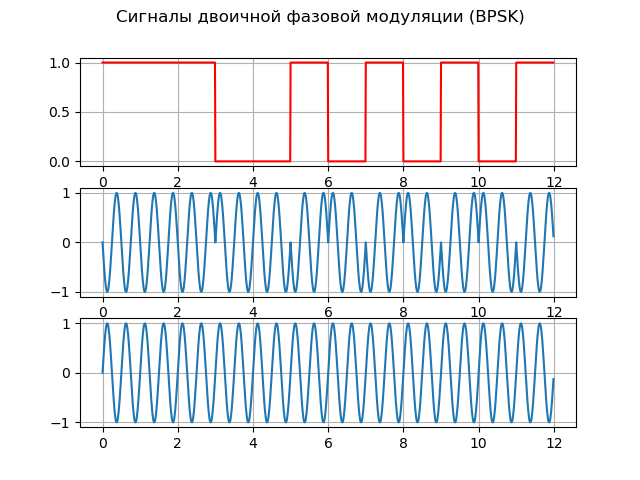
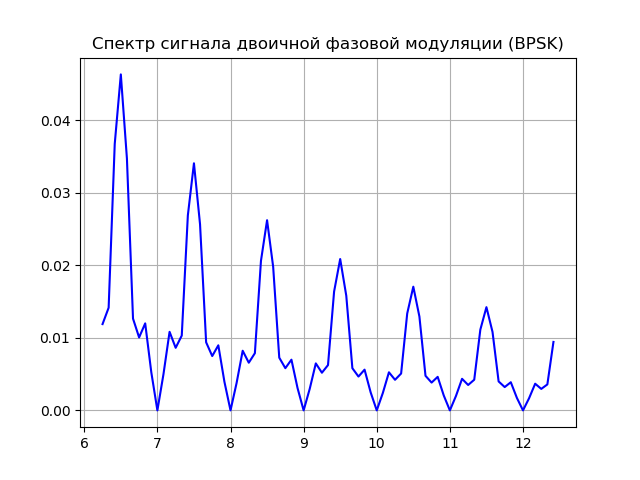
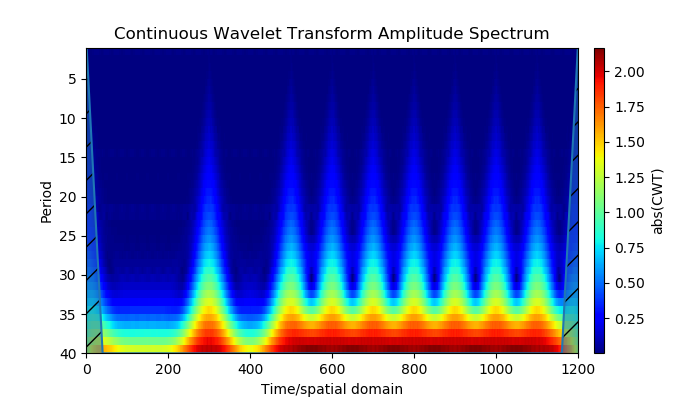
Model Sumber


Sinyal harmonik navigasi termodulasi fase dari satelit atau pesawat ruang angkasa memiliki bentuk:

x=a(2 pifct+ jumlahsncos(2 pifnt)),

di mana frekuensi pembawa fc=$8. GHz

Sinyal memiliki beberapa parameter yang dikendalikan: amplitudo osilasi modulasi ke-n
sn, frekuensinya fc dan amplitudo osilasi pembawa a.

Untuk mendapatkan fungsi korelasi di mana lobus sampingnya ditekan sebanyak mungkin dan puncak korelasi tersempit tercapai, kita akan memvariasikan nilai frekuensi menggunakan nilai 2, 4, 8, dan 16 MHz dan indeks modulasi dalam kisaran dari 0 hingga 2π dalam peningkatan π. Biarkan saya memberi Anda daftar program untuk pencarian parameter fungsi termodulasi fase untuk hasil akhir:

Daftar
 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**18 #-  delay =4 # t1 =linspace(0, T, N) t2 = linspace(0 + delay, T + delay, N) fs = (N - 1)/T #  ax = 1e-3 bx = 2e-6 ay = 2e-3 by = 3e-6 aex = 1e-3 + 30e-9 bex = 2e-6 + 10e-12 aey = 2e-3 + 30e-9 bey = 3e-6 + 10e-12 taux = ax + bx*t1 tauy = ay + by*t2 tauex = aex + bex*t1 tauey = aey + bey*t2 #  # print(" :") No1 = No2 = 0 fc = 8.4e9 #  #   A1 = 2*pi A2 = 0 A3 =2*pi A4 = 4*pi #   fm1 = 2e6 fm2 = 4e6 fm3 = 8e6 fm4 = 16e6 f = 20e6 #     ff = fc - f #   fco = 16e6 #     def korel(x,y): #  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s #   def phase_shifter2(x, t, tau, b): L = linspace(0,N,N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t) return s # def heterodyning(x, t): return x*exp(-1j*2*pi*ff*t) # def filt(S): p = signal.convolve(S,h) y = p[int((n - 1)/2) : int(N+(n - 1)/2)] return y def corr(y1, y2): Y1 = fft(y1) Y2 = fft(y2) # Z = Y1*Y2.conjugate() # z = ifft(Z)/N return sqrt(z.real**2 + z.imag**2) #   def graf(c, t): c1=c[int(N/2):N] c2=c[0:int(N/2)] C = concatenate((c1, c2)) xlabel(',') ylabel('') title('   ') grid(True) plot(t*1e9 - 250, C, 'b',label="    \n    ") legend(loc='best') show() noise1 = random.uniform(-No1, No1, size = N) #   noise2 =noise1 #   x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1) y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2) n = 100001 #  #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) x2 = filt(x1) y2 = filt(y1) X2 = phase_shifter2(x2, t1, tauex, bex) Y2 = phase_shifter2(y2, t2, tauey, bey) Corr = corr(X2, Y2) graf(Corr, t1) #     ##for A1 in [pi/4,pi/2,pi]: ## x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)) ## y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2)) ## korel(x,y) ##for fm in [ fm2,fm3,fm4]: ## A1=2*pi ## x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm*t1)) ## y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm*t2)) ## korel(x,y) #     ##for fm2 in [ fm1, fm2,fm3,fm4]: ## A1=2*pi ## A2=2*pi ## fm1=2e6 ## x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1)) ## y =cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2)+A2*np.cos(2*pi*fm2*t2)) ## korel(x,y) x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1)+A3*cos(2*pi*fm3*t1)+A4*cos(2*pi*fm4*t1)) y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2) +A2*cos(2*pi*fm2*t2) +A3*cos(2*pi*fm3*t2)+A4*cos(2*pi*fm4*t2)) korel(x,y)


Kami mendapatkan:



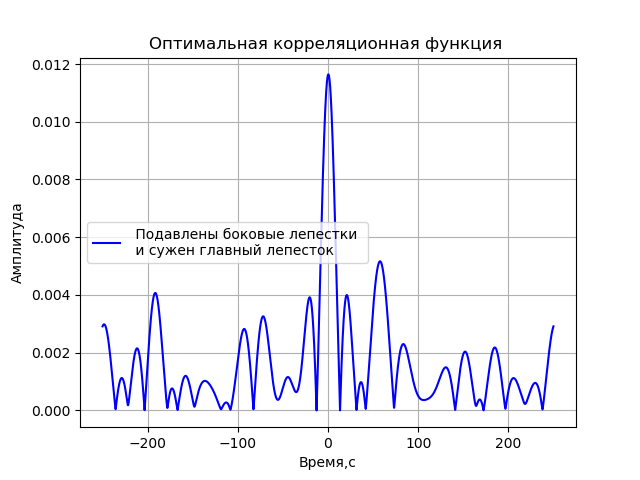
Fungsi yang dihasilkan memiliki bentuk:

x=cos(2 pifct+2 picos(2 pi106t)+2 picos(2 pi108t)+4 picos(2 pi1016t)).(1)

Lebih lanjut, fungsi ini akan digunakan untuk mensimulasikan VLBI.

Model generator kebisingan mensimulasikan interferensi yang diterima bersama dengan sinyal dari luar angkasa dan dari atmosfer Bumi


Fungsi (1) sinyal navigasi termodulasi fase dapat diterapkan ke kedua saluran interferometer radio, tetapi perlu untuk mempertimbangkan penundaan sinyal di saluran kedua dan kebisingan di kedua saluran seperti yang ditunjukkan dalam daftar berikut:

Daftar
 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  delay =1e-7 # t1 =linspace(0, T, N) t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9 #  # print(" :") No1 = No2 = 0.5 noise1 = random.uniform(-No1, No1, size = N) #   noise2 =random.uniform(-No1, No1, size = N) #   x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) title("    \n    ") plot(t1,x,label="  ") plot(t2,y,label="  c ") x=noise1;y=noise2 plot(t1,x,label="  ") plot(t2,y,label="  ") legend(loc='best') grid(True) figure() noise1_2 = np.random.uniform(-No1, No1, size = N) #     sko=np.std(noise1_2) mo= np.mean(noise1_2) sko=round(sko,2) mo=round(mo,2) title("  . :%s,:%s"%(sko,mo)) ylabel('   ') xlabel('  ') hist(noise1_2,bins='auto') show()


Kami mendapatkan:



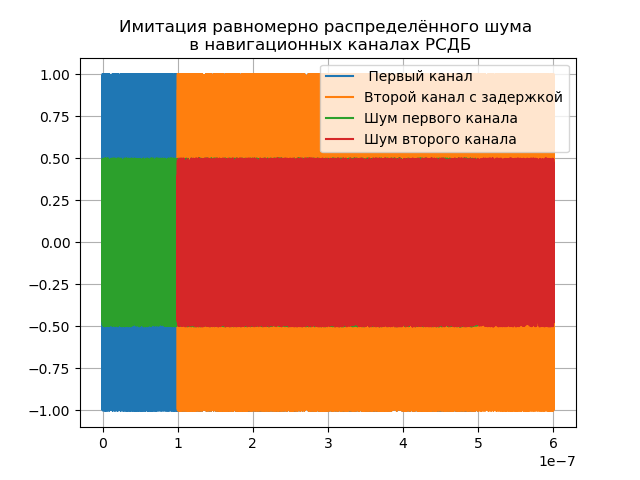
Penundaan keterlambatan = 1e-7 diatur untuk demonstrasi, pada kenyataannya itu tergantung pada pangkalan dan dapat mencapai empat atau lebih unit.



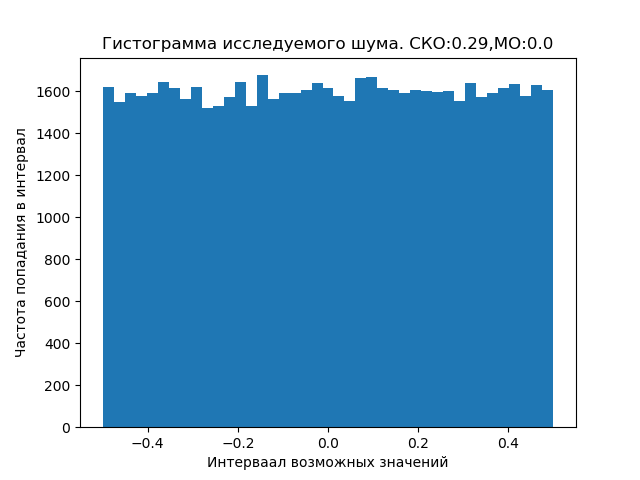
Suara-suara baik kosmik maupun dekat Bumi dapat didistribusikan menurut hukum yang berbeda dari seragam yang diberikan, yang memerlukan studi khusus.

Memodelkan efek Doppler


Karena kenyataan bahwa Bumi memiliki bentuk bulat dan berputar di sekitar sumbunya, sinyal dari ruang angkasa tiba di antena dengan penundaan berbeda. Untuk alasan ini, perlu untuk menggeser sinyal dalam waktu dan memperhitungkan frekuensi Doppler. Kami akan mempertimbangkan bahwa penundaan bervariasi menurut hukum linier:

 taux(t)=ax+bxt,(2)

dimana ax=1..3 cdot10−3 ms, dan bx=1..3 cdot10−6 ms Fase Doppler ditemukan sebagai turunan dari penundaan:

fdx= fracd tau(t)dt=bx,(3)

Sinyal yang diterima akan terlihat seperti:

 hatx=x(t− taux)ej2 pifdxt,
di mana x (t) adalah sinyal yang dipancarkan dari pesawat ruang angkasa.

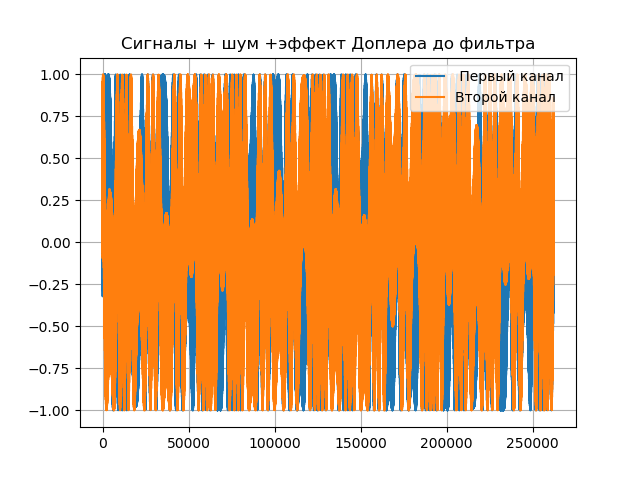
Demonstrasi efek Doppler diperlihatkan dalam daftar berikut:

Daftar
 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7#   N = 2**16 #-  t1 =linspace(0, T, N) delay =4 # t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9#  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s.real figure() title("    ") ax = 3e-3 bx = 3e-6 taux = ax + bx*t1 x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) sx=phase_shifter1(x, t1, taux, bx ) plot(t1[0:150],x[0:150],label="      ") plot(t1[0:150],sx[0:150],label="      ") grid(True) legend(loc='best') figure() title("    ") ay = 2e-3 by = 3e-6 tauy = ay + by*t2 y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) sy= phase_shifter1(y, t2, tauy, by) plot(t2[0:150],y[0:150],label="      ") plot(t2[0:150],sy[0:150],label="      ") grid(True) legend(loc='best') show()


Kami mendapatkan:





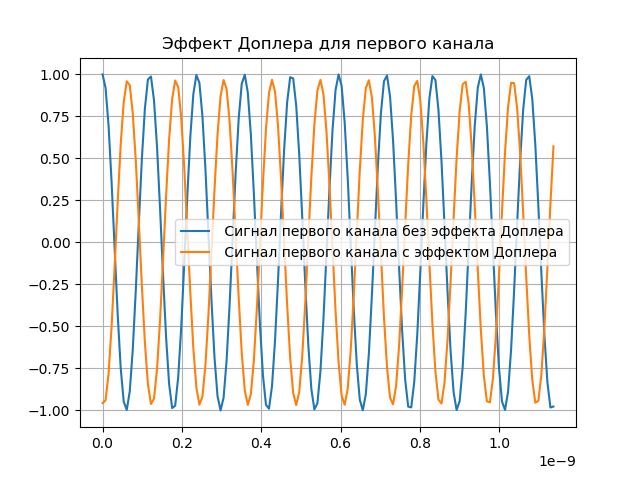
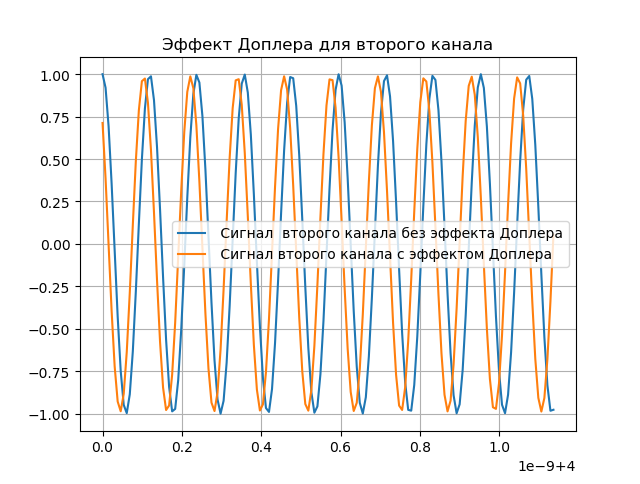
Kompensasi Pemodelan Doppler


Jelas, perubahan yang dilakukan pada sinyal harus dikompensasi. Untuk tujuan ini, sistem berisi dukungan untuk fase penundaan dan Doppler. Setelah sinyal melewati sistem registrasi, penundaan diperkenalkan:

 tauex(t)=ax+bext,(4)

Ini akan mempertimbangkan bahwa keterlambatan dihitung dengan akurasi tertentu, sedemikian rupa  kiri|aex−ax right|<30 ns  kiri|bex−bx right|<10 ns, yaitu Ini akan sedikit berbeda dari yang dia buat sebelumnya. Jelaslah bahwa keterlambatan diperkenalkan dengan tanda kebalikan dari yang diperkenalkan sebelumnya.

Sinyal yang diterima akan terlihat seperti:

 hatx= tildex(t​​+ tauex)e−j2 pifdet.(5)

Kompensasi efek Doppler ditunjukkan dalam daftar berikut:

Daftar
 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7#   N = 2**16 #-  t1 =linspace(0, T, N) delay =4 # t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9#  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s.real ax = 3e-3 bx = 3e-6 taux = ax + bx*t1 x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) sx=phase_shifter1(x, t1, taux, bx ) ay = 2e-3 by = 3e-6 tauy = ay + by*t2 y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) sy= phase_shifter1(y, t2, tauy, by) def phase_shifter2(x, t, tau, b): L = linspace(0,N,N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t) return s.real figure() title("     ") aex = 1e-3 + 30e-9 bex = 2e-6 + 10e-12 tauex = aex + bex*t1 x1 = phase_shifter2(sx, t1, tauex, bex) plot(t1[0:150],x1[0:150],label="      ") grid(True) legend(loc='best') figure() title("     ") aey = 2e-3 + 30e-9 bey = 3e-6 + 10e-12 tauey = aey + bey*t2 y2 = phase_shifter2(sy, t2, tauey, bey) plot(t2[0:150],y2[0:150],label="      ") grid(True) legend(loc='best') show()


Kami mendapatkan:





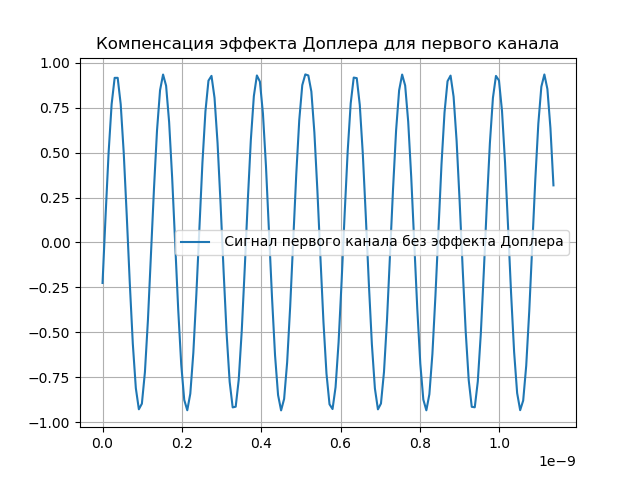
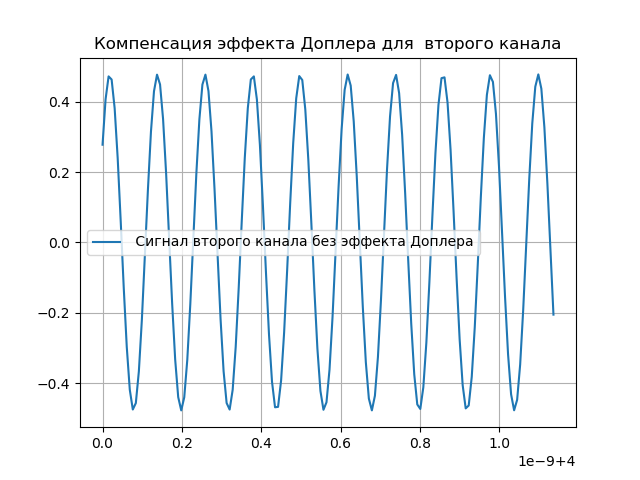
Simulasi sinyal heterodyne


Setelah sinyal memasuki sistem registrasi, konversi frekuensi terjadi, yang juga disebut heterodyning. Ini adalah transformasi non-linear di mana dari sinyal dua frekuensi berbeda f1 dan f2 sinyal frekuensi perbedaan disorot - f= kiri|f1−f2 right.| Frekuensi sinyal osilator lokal akan sama dengan perbedaan antara frekuensi sinyal yang diselidiki dan frekuensi yang ingin Anda dapatkan setelah transfer. Heterodyning dilakukan dengan menggunakan generator tambahan osilasi harmonik - osilator lokal dan elemen nonlinier. Secara matematis, heterodyning adalah perkalian sinyal oleh eksponen:

xg= hatxej2 pifgt,(6)
dimana fg - sinyal osilator lokal.

Program untuk heterodyning:

Daftar
 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  t1 =linspace(0, T, N) fs = (N - 1)/T #  fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   def spectrum_wavelet(y,a,b,c,e,st):#   n = len(y)#   k = arange(n) T = n / a frq = k / T #    frq = frq[np.arange(int(n/2))] #    Y = fft(y)/ n # FFT    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))]) plot(frq[b:c],abs(Y)[b:c],e,label=st) #   xlabel('Freq (Hz)') ylabel('|Y(freq)|') legend(loc='best') grid(True) x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) a=fs;b=0;c=20000;e='g'; st='     ' spectrum_wavelet(x,a,b,c,e,st) show()


Kami mendapatkan:





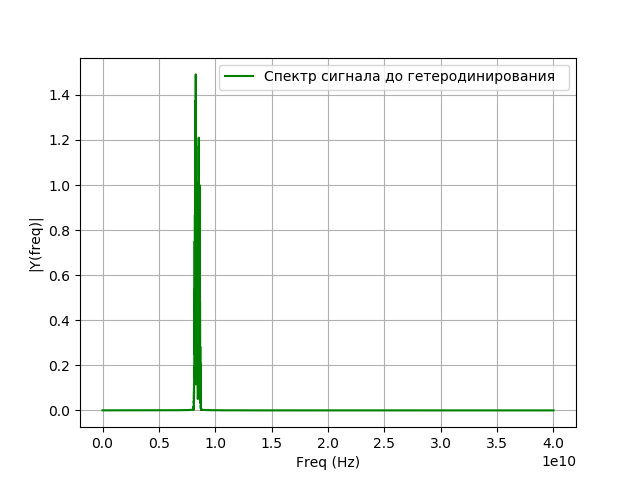
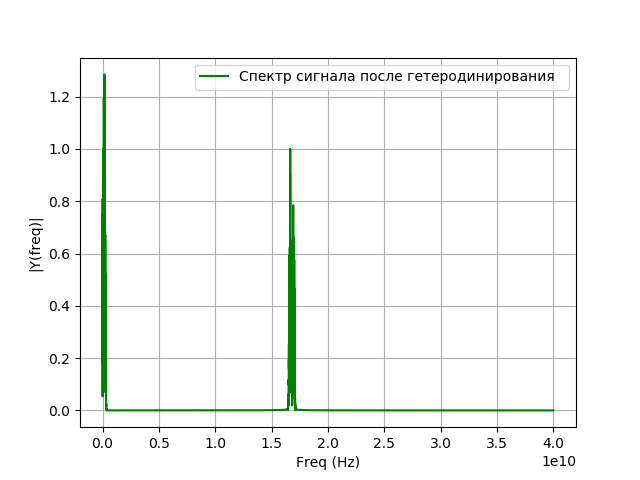
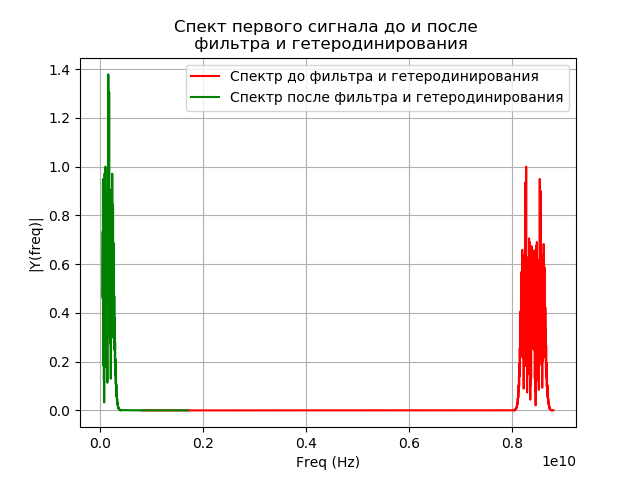
Pemodelan penyaringan sinyal setelah heterodyning


Setelah heterodyning, sinyal memasuki filter bandpass. Filter Passband (PP) fpass=32 MHz Respons impuls filter dihitung dengan metode jendela menggunakan fungsi library signal.firwin. Untuk mendapatkan sinyal pada output filter, konvolusi filter dan sinyal dalam domain waktu dilakukan. Integral konvolusi untuk kasus kami mengambil bentuk:

 checkx(t)= int+ infty− inftyxg(t)h(t−t′)dt,(7)

di mana h (t) adalah respons impuls dari filter.

Konvolusi ditemukan menggunakan fungsi library signal.convolve. Sinyal terdaftar, dengan mempertimbangkan heterodyning dan penyaringan akun, disajikan dalam bentuk formula

 checkx(t)=( hatx(t)e−j2 pifgt)∗h

di mana konvolusi ditunjukkan oleh *.

Program untuk pemodelan filtrasi:

Daftar
 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  t1 =linspace(0, T, N) fs = (N - 1)/T #  fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   def spectrum_wavelet(y,a,b,c,e,st):#   n = len(y)#   k = arange(n) T = n / a frq = k / T #    frq = frq[np.arange(int(n/2))] #    Y = fft(y)/ n # FFT    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))]) plot(frq[b:c],abs(Y)[b:c],e,label=st) #   xlabel('Freq (Hz)') ylabel('|Y(freq)|') legend(loc='best') grid(True) x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) def heterodyning(x, t): return x*exp(-1j*2*pi*ff*t).real z=heterodyning(x, t1) fco = 16e6 #     n = 100001 #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) def filt(S): p = signal.convolve(S,h) y = p[int((n - 1)/2) : int(N+(n - 1)/2)] return y q=filt(z) a=fs;b=0;c=850;e='g'; st='    ' spectrum_wavelet(q,a,b,c,e,st) show()


Kami mendapatkan:



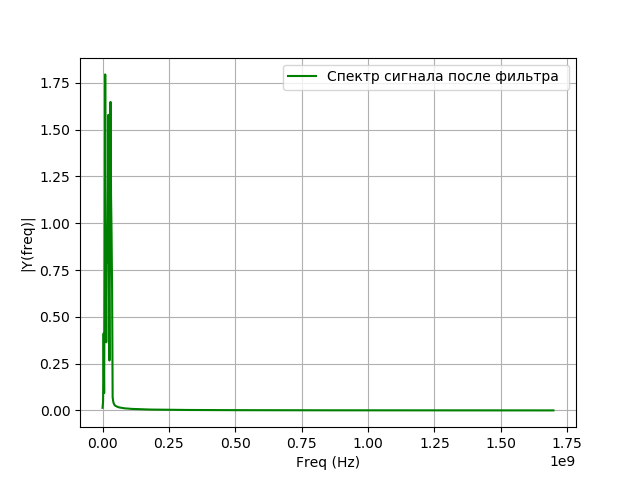
Konverter sinyal digital untuk VLBI terutama menggunakan filter dengan respon impuls terbatas (FIR), karena mereka memiliki sejumlah keunggulan dibandingkan dengan filter dengan respon impuls tak terbatas (IIR):

  1. Filter FIR dapat memiliki respon fase linier ketat dalam kasus simetri respon impuls (IM). Ini berarti bahwa menggunakan filter seperti itu, distorsi fase dapat dihindari, yang sangat penting untuk interferometri radio. Filter dengan respon impuls tak terbatas (IIR) tidak memiliki sifat simetri dari mereka dan tidak dapat memiliki respon fase linier.
  2. Filter FIR adalah non-rekursif, yang berarti selalu stabil. Stabilitas filter IIR tidak selalu dapat dijamin.
  3. Konsekuensi praktis dari penggunaan sejumlah bit untuk menerapkan filter secara signifikan kurang signifikan untuk filter FIR.

Dalam daftar di atas, model filter bandpass FIR diimplementasikan menggunakan metode jendela, urutan filter dipilih sehingga bentuk respon frekuensi filter dekat dengan persegi panjang. Jumlah koefisien dari filter yang disimulasikan adalah n = 100001, yaitu urutan filter adalah P = 100000.

Program untuk membangun respons frekuensi dan respons fase dari filter FIR yang diperoleh:

Daftar
 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  t1 =linspace(0, T, N) fs = (N - 1)/T #  fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   fco = 16e6 #     n = 100001 #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) #  def AFC(A, n, f, deltf, min, max): plot((fftfreq (n, 1./fs)/1e9), 10*log10(abs(fft(A))), 'k') axvline((f - fco)/1e9, color = 'red', label='  ') axvline((f + fco)/1e9, color = 'red') axhline(-3, color='green', linestyle='dashdot') text(8.381, -3, repr(round(-3, 9))) xlabel(', ') ylabel(' , ') title('') grid(True) axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max]) grid(True) show() #  def PFC(A, n, f, deltf, min, max): plot(fftfreq(n, 1./fs)/1e9, np.unwrap(np.angle(fft(A))), 'k') axvline((f - fco)/1e9, color='red', label='  ') axvline((f + fco)/1e9, color='red') xlabel(', ') ylabel(',') title('') axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max]) #  grid(True) legend(loc='best') show() AFC(h, n, f, 20e6, -30, 1) PFC(h, n, f, 20e6, -112, 0)


Kami mendapatkan:





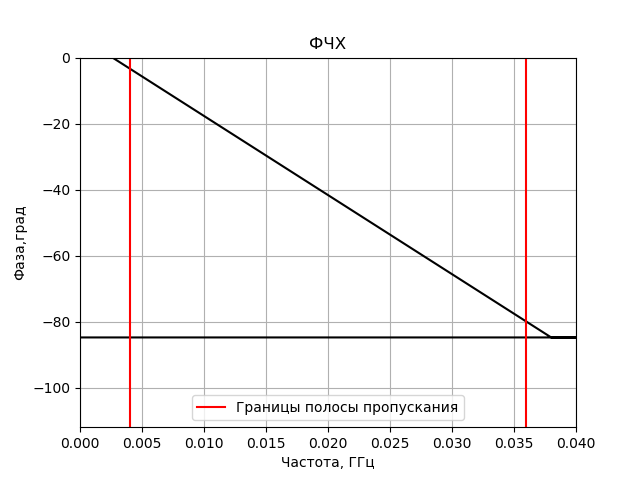
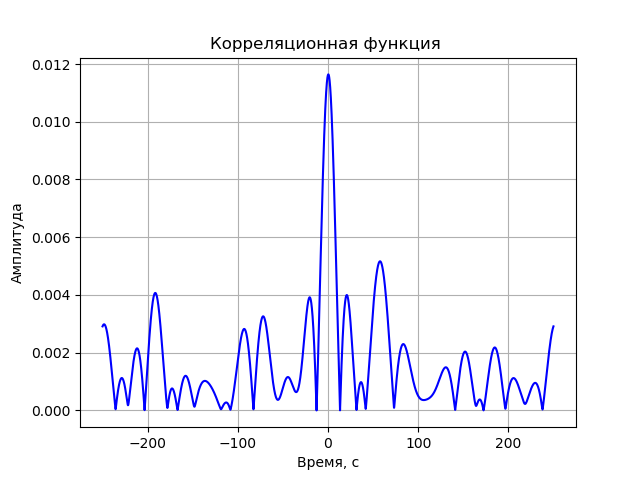
Model korelator valas


Selanjutnya, setiap sinyal mengalami transformasi Fourier cepat (FFT). FFT diimplementasikan menggunakan fungsi fft library dari scipy.fftpack. Spektrum yang dihasilkan adalah konjugat kompleks yang dikalikan:

S(j omega)=S1(j omega)∗S2(j omega)=(a1+jb1)∗(a2−jb2)=a1a2+b1b2+j(b1a2−a1b2)

Tindakan terakhir adalah kebalikan dari FFT. Karena amplitudo fungsi korelasi menarik, sinyal yang dihasilkan harus dikonversi oleh rumus:

A= sqrtre2+im2

Program untuk fungsi korelasi tanpa memperhitungkan distorsi sistem registrasi:

Daftar
 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7#   N = 2**16 #-  t1 =linspace(0, T, N) delay =4 # t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9#  def corr(y1, y2): Y1 = fft(y1) Y2 = fft(y2) # Z = Y1*Y2.conjugate() # z = ifft(Z)/N q=sqrt(z.real**2 + z.imag**2) c1=q[int(N/2):N] c2=q[0:int(N/2)] C = concatenate((c1, c2)) xlabel(',') ylabel('') title('  ') grid(True) plot(t1*1e9 - 250, C, 'b') show() x= cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) corr(x, y)


Kami mendapatkan:



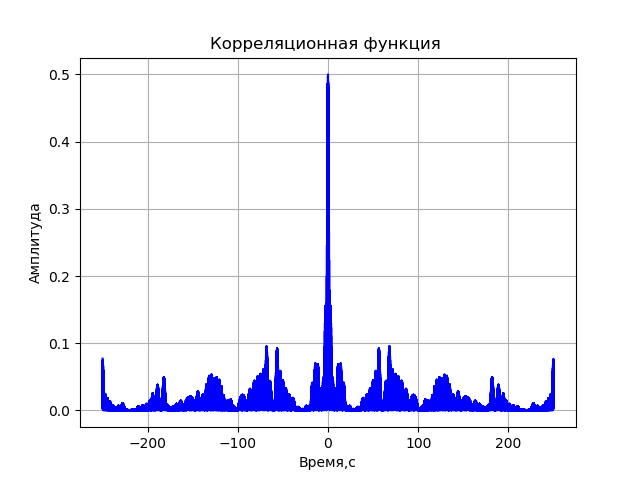
Daftar lengkap model komputer VLBI:


Daftar
 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**18 #-  delay =4 # t1 =linspace(0, T, N) t2 = linspace(0 + delay, T + delay, N) fs = (N - 1)/T #  ax = 1e-3 bx = 2e-6 ay = 2e-3 by = 3e-6 aex = 1e-3 + 30e-9 bex = 2e-6 + 10e-12 aey = 2e-3 + 30e-9 bey = 3e-6 + 10e-12 taux = ax + bx*t1 tauy = ay + by*t2 tauex = aex + bex*t1 tauey = aey + bey*t2 #  # print(" :") No1 = No2 = 0 #    # print(" :") fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   fco = 16e6 #     #  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s #   def phase_shifter2(x, t, tau, b): L = linspace(0,N,N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t) return s # def heterodyning(x, t): return x*exp(-1j*2*pi*ff*t) # def filt(S): p = signal.convolve(S,h) y = p[int((n - 1)/2) : int(N+(n - 1)/2)] return y def spectrum_wavelet(y,a,b,c,e,st):#   n = len(y)#   k = arange(n) T = n / a frq = k / T #    frq = frq[np.arange(int(n/2))] #    Y = fft(y)/ n # FFT    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))]) plot(frq[b:c],abs(Y)[b:c],e,label=st) #   xlabel('Freq (Hz)') ylabel('|Y(freq)|') legend(loc='best') grid(True) def corr(y1, y2): Y1 = fft(y1) Y2 = fft(y2) # Z = Y1*Y2.conjugate() # z = ifft(Z)/N return sqrt(z.real**2 + z.imag**2) #   def graf(c, t): c1=c[int(N/2):N] c2=c[0:int(N/2)] C = concatenate((c1, c2)) xlabel(', ') ylabel('') title('  ') grid(True) plot(t*1e9 - 250, C, 'b') show() noise1 = random.uniform(-No1, No1, size = N) #   noise2 =random.uniform(-No1, No1, size = N) #   def signal_0(): x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) return x,y title(" +  +   ") x,y= signal_0() x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1) plot(x1.real,label="  ") y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2) plot(y1.real,label=" ") grid(True) legend(loc='best') show() n = 100001 #  #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) title("- -    ") x2 = filt(x1) plot(x2.real,label="  ") y2 = filt(y1) plot(y2.real,label="  ") grid(True) legend(loc='best') show() plt.title("      \n   ") a=fs;b=400;c=4400;e='r' st="    " spectrum_wavelet(x,a,b,c,e,st) a=fs;b=20;c=850;e='g' st="    " spectrum_wavelet(x1,a,b,c,e,st) show() X2 = phase_shifter2(x2, t1, tauex, bex) Y2 = phase_shifter2(y2, t2, tauey, bey) Corr = corr(X2, Y2) graf(Corr, t1)


Kami mendapatkan:





Kesimpulan


  1. Sejarah singkat perkembangan astronomi radio diberikan.
  2. Keadaan jaringan VLBI saat ini dianalisis.
  3. Masalah yang dipecahkan dengan menggunakan jaringan VLBI dipertimbangkan.
  4. Alat Python membangun model sinyal navigasi dengan modulasi fase biner (dua posisi) - BPSK (tombol shift fase biner). Model ini menggunakan analisis wavelet modulasi fase.
  5. Model sumber sinyal telah diperoleh, yang memungkinkan seseorang untuk menentukan parameter modulasi yang menyediakan fungsi korelasi optimal sesuai dengan kriteria untuk menekan lobus samping dan amplitudo maksimum lobus pusat.
  6. Model jaringan VLBI yang disederhanakan diperoleh, dengan mempertimbangkan kebisingan akun dan efek Doppler. Fitur penyaringan menggunakan filter dengan respon impuls terbatas dipertimbangkan.
  7. Setelah ringkasan singkat dari teori, semua model dilengkapi dengan program demonstrasi yang memungkinkan Anda untuk melacak pengaruh parameter model.

Source: https://habr.com/ru/post/id458252/

More articles:


All Articles