Kami terus berbicara tentang konferensi tentang statistik dan pembelajaran mesin AISTATS 2019. Dalam posting ini kami akan menganalisis artikel tentang model mendalam dari ansambel pohon, mencampur regularisasi untuk data yang sangat jarang, dan perkiraan waktu validasi silang yang hemat waktu.

Algoritma Hutan Dalam: Eksplorasi Model Non-NN Deep berdasarkan Modul Non-Diferensial
Zhi-Hua Zhou (Universitas Nanjing)
→ Presentasi
→ Artikel
Implementasi - di bawah ini
Seorang profesor dari Tiongkok berbicara tentang ansambel pohon, yang penulis sebut sebagai pelatihan mendalam pertama tentang modul yang tidak dapat dibedakan. Ini mungkin tampak seperti pernyataan yang terlalu keras, tetapi profesor ini dan indeks-H 95-nya diundang sebagai pembicara, fakta ini memungkinkan kita untuk menganggap pernyataan itu lebih serius. Teori dasar Deep Forest telah dikembangkan sejak lama, artikel aslinya sudah 2017 (hampir 200 kutipan), tetapi penulis menulis perpustakaan dan setiap tahun mereka meningkatkan algoritma dalam kecepatan. Dan sekarang, tampaknya, mereka telah mencapai titik di mana teori yang indah ini akhirnya dapat dipraktikkan.
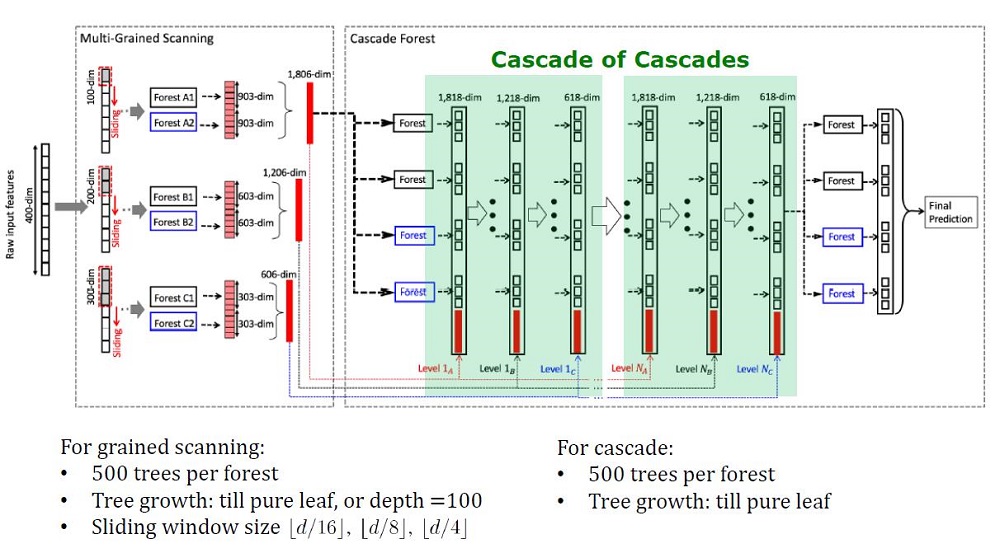
Pandangan umum arsitektur Deep Forest
Latar belakang
Model mendalam, yang sekarang dipahami sebagai jaringan saraf dalam, digunakan untuk menangkap dependensi data yang kompleks. Selain itu, ternyata meningkatkan jumlah lapisan lebih efisien daripada meningkatkan jumlah unit pada setiap lapisan. Tetapi jaringan saraf memiliki kelemahan:
- Dibutuhkan banyak data untuk tidak berlatih kembali,
- Dibutuhkan banyak sumber daya komputasi untuk belajar dalam jumlah waktu yang wajar,
- Terlalu banyak hiperparameter yang sulit dikonfigurasi secara optimal
Selain itu, elemen jaringan syaraf dalam adalah modul yang dapat dibedakan yang belum tentu efektif untuk setiap tugas. Terlepas dari kerumitan jaringan saraf, algoritma konseptual sederhana, seperti hutan acak, sering bekerja lebih baik atau tidak jauh lebih buruk. Tetapi untuk algoritma seperti itu, Anda perlu merancang fitur secara manual, yang juga sulit dilakukan secara optimal.
Para peneliti telah memperhatikan bahwa ansambel pada Kaggle: “sangat sempurna”, dan terinspirasi oleh kata-kata Scholl dan Hinton bahwa diferensiasi adalah sisi terlemah dari Deep Learning, mereka memutuskan untuk membuat ansambel pohon dengan properti DL.
Slide “Cara membuat ansambel yang bagus”
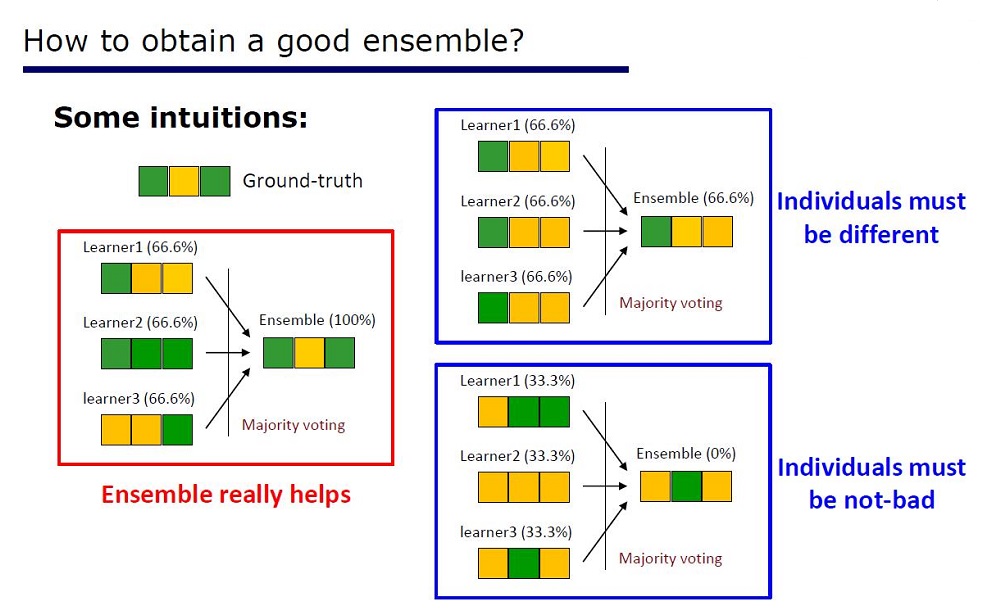
Arsitekturnya disimpulkan dari sifat-sifat ansambel: unsur-unsur ansambel tidak boleh sangat buruk dalam kualitas dan berbeda.
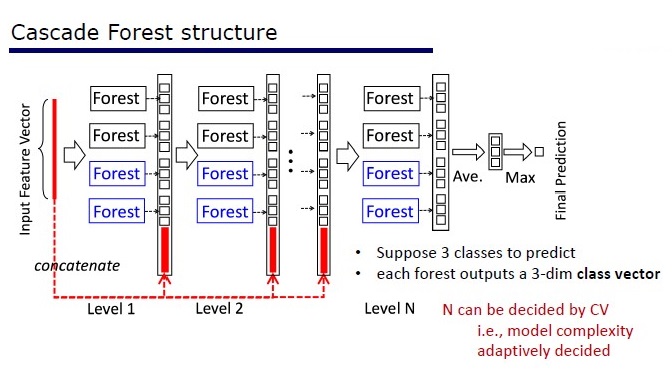
GcForest terdiri dari dua fase: Cascade Forest dan Multi-Grained Scanning. Selain itu, agar kaskade tidak berlatih kembali, terdiri dari 2 jenis pohon - salah satunya adalah pohon yang benar-benar acak yang dapat digunakan pada data yang tidak terisi. Jumlah lapisan ditentukan di dalam algoritma cross-validation.
Dua jenis pohon
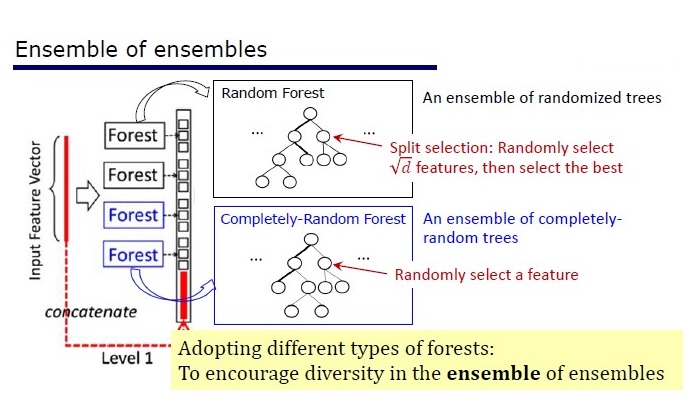
Hasil
Selain hasil pada dataset standar, penulis mencoba menggunakan gcForest pada transaksi sistem pembayaran Cina untuk mencari penipuan dan mendapatkan F1 dan AUC jauh lebih tinggi daripada LR dan DNN. Hasil ini hanya dalam presentasi, tetapi kode untuk dijalankan pada beberapa dataset standar ada di Git.
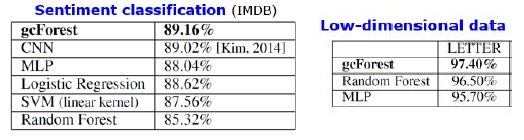
Hasil substitusi algoritma. mdDF adalah optimal Margin Distribution Deep Forest, varian dari gcForest
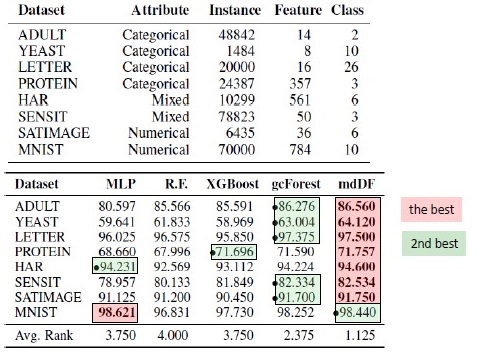
Pro:
- Beberapa hiperparameter, jumlah lapisan disesuaikan secara otomatis di dalam algoritma
- Pengaturan default dipilih untuk bekerja dengan baik pada banyak tugas.
- Kompleksitas adaptif model, pada data kecil - model kecil
- Tidak perlu mengatur fitur
- Ini berfungsi sebanding dalam kualitas dengan jaringan saraf yang dalam, dan kadang-kadang lebih baik
Cons:
- Tidak dipercepat pada GPU
- Dalam gambar kehilangan DNN
Jaringan saraf memiliki masalah redaman gradien, sementara hutan yang dalam memiliki masalah “diversifikasi menghilang”. Karena ini adalah ansambel, semakin banyak elemen "berbeda" dan "baik" untuk digunakan, semakin tinggi kualitasnya. Masalahnya adalah bahwa penulis telah mencoba hampir semua pendekatan klasik (pengambilan sampel, pengacakan). Selama tidak ada penelitian dasar baru yang muncul pada topik “perbedaan”, akan sulit untuk meningkatkan kualitas hutan yang dalam. Tetapi sekarang mungkin untuk meningkatkan kecepatan komputasi.
Reproduksibilitas hasil
Saya tertarik oleh XGBoost pada data tabular, dan saya ingin mereproduksi hasilnya. Saya mengambil dataset Dewasa dan menerapkan GcForestCS (versi yang sedikit dipercepat dari GcForest) dengan parameter dari penulis artikel dan XGBoost dengan parameter default. Dalam contoh yang dimiliki penulis, fitur kategorikal sudah dipra-proses sebelumnya, tetapi tidak ditunjukkan caranya. Akibatnya, saya menggunakan CatBoostEncoder dan metrik lainnya - ROC AUC. Hasilnya berbeda secara statistik - XGBoost menang. Waktu operasi XGBoost dapat diabaikan, sementara gcForestCS memiliki 20 menit masing-masing cross-validasi pada 5 kali lipat. Di sisi lain, penulis menguji algoritma pada dataset yang berbeda, dan menyesuaikan parameter untuk dataset ini dengan preprocessing fitur mereka.
Kode dapat ditemukan di sini .
Implementasi
→ Kode resmi dari penulis artikel
→ Modifikasi yang ditingkatkan resmi, lebih cepat, tetapi tidak ada dokumentasi
→ Implementasi lebih sederhana
PcLasso: laso memenuhi regresi komponen utama
J. Kenneth Tay, Jerome Friedman, Robert Tibshirani (Universitas Stanford)
→ Artikel
→ Presentasi
→ Contoh penggunaan
Pada awal 2019, J. Kenneth Tay, Jerome Friedman, dan Robert Tibshirani dari Stanford University mengusulkan metode pengajaran baru dengan seorang guru, terutama cocok untuk data yang jarang.
Para penulis artikel memecahkan masalah menganalisis data pada studi ekspresi gen, yang dijelaskan dalam Zeng & Breesy (2016). Target adalah status mutasi gen p53, yang mengatur ekspresi gen dalam menanggapi berbagai sinyal stres seluler. Tujuan dari penelitian ini adalah untuk mengidentifikasi prediktor yang berkorelasi dengan status mutasi p53. Data terdiri dari 50 baris, 17 di antaranya diklasifikasikan sebagai normal dan 33 lainnya membawa mutasi pada gen p53. Menurut analisis dalam Subramanian et al. (2005) 308 set gen yang antara 15 dan 500 dimasukkan dalam analisis ini. Kit gen ini mengandung total 4.301 gen dan tersedia dalam paket grpregOverlap R. Saat memperluas data untuk memproses grup yang tumpang tindih, 13.237 kolom adalah output. Para penulis artikel menggunakan metode pcLasso, yang membantu meningkatkan hasil model.
Dalam gambar kita melihat peningkatan AUC saat menggunakan "pcLasso"

Esensi dari metode ini
Metode menggabungkan  -regulasi dengan
-regulasi dengan  , yang mempersempit vektor koefisien ke komponen utama dari matriks fitur. Mereka menyebut metode yang diusulkan "komponen laso inti" ("pcLasso" tersedia di R). Metode ini bisa sangat kuat jika variabel sebelumnya dikelompokkan (pengguna memilih apa dan bagaimana mengelompokkan). Dalam hal ini, pcLasso memampatkan setiap grup dan mendapatkan solusi sesuai dengan komponen utama grup ini. Dalam proses penyelesaian, pemilihan kelompok yang signifikan di antara yang tersedia juga dilakukan.
, yang mempersempit vektor koefisien ke komponen utama dari matriks fitur. Mereka menyebut metode yang diusulkan "komponen laso inti" ("pcLasso" tersedia di R). Metode ini bisa sangat kuat jika variabel sebelumnya dikelompokkan (pengguna memilih apa dan bagaimana mengelompokkan). Dalam hal ini, pcLasso memampatkan setiap grup dan mendapatkan solusi sesuai dengan komponen utama grup ini. Dalam proses penyelesaian, pemilihan kelompok yang signifikan di antara yang tersedia juga dilakukan.
Kami menyajikan matriks diagonal dari dekomposisi singular dari matriks fitur terpusat  sebagai berikut:
sebagai berikut:
Kami mewakili dekomposisi singular kami dari matriks berpusat X (SVD) sebagai  dimana
dimana  Merupakan matriks diagonal yang terdiri dari nilai singular. Dalam bentuk ini
Merupakan matriks diagonal yang terdiri dari nilai singular. Dalam bentuk ini  - Regularisasi dapat diwakili:
- Regularisasi dapat diwakili:
 dimana
dimana  - matriks diagonal yang berisi fungsi kuadrat dari nilai singular:
- matriks diagonal yang berisi fungsi kuadrat dari nilai singular: %2C%E2%80%A6%2CZ_%7B22%7D%3Df_2%20(d_1%5E2%2Cd_2%5E2%2C%E2%80%A6%2Cd_m%5E2%20)) .
.
Secara umum, dalam  -regulasi
-regulasi  untuk semua
untuk semua  yang sesuai
yang sesuai  . Mereka menyarankan meminimalkan fungsi berikut:
. Mereka menyarankan meminimalkan fungsi berikut:
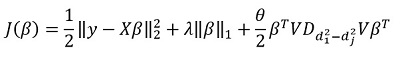
Di sini  - matriks perbedaan elemen diagonal
- matriks perbedaan elemen diagonal  . Dengan kata lain, kami mengontrol vektor
. Dengan kata lain, kami mengontrol vektor  menggunakan hyperparameter juga
menggunakan hyperparameter juga  .
.
Mengubah ungkapan ini, kami mendapatkan solusinya:
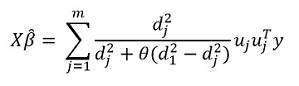
Tetapi "fitur" utama dari metode ini, tentu saja, adalah kemampuan untuk mengelompokkan data, dan atas dasar kelompok-kelompok ini untuk menyoroti komponen utama kelompok. Kemudian kami menulis ulang solusi kami dalam bentuk:
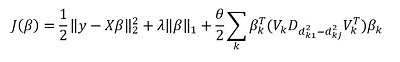
Di sini  - vektor subvektor
- vektor subvektor  sesuai dengan grup k,
sesuai dengan grup k, ) - nilai tunggal
- nilai tunggal  diatur dalam urutan menurun, dan
diatur dalam urutan menurun, dan  - matriks diagonal
- matriks diagonal 
Beberapa catatan tentang solusi fungsional target:
Fungsi obyektif adalah cembung, dan komponen yang tidak halus dapat dipisahkan. Oleh karena itu, dapat dioptimalkan secara efektif menggunakan gradient descent.
Pendekatannya adalah dengan mengkomit banyak nilai  (termasuk nol, masing-masing, mendapatkan standar
(termasuk nol, masing-masing, mendapatkan standar  -regulasi), dan kemudian mengoptimalkan:
-regulasi), dan kemudian mengoptimalkan:  mengambil
mengambil  . Dengan demikian, parameter
. Dengan demikian, parameter  dan
dan  dipilih untuk validasi silang.
dipilih untuk validasi silang.
Parameter  sulit diartikan. Dalam perangkat lunak (paket pcLasso), pengguna sendiri menetapkan nilai parameter ini, yang termasuk dalam interval [0,1], di mana 1 sesuai dengan
sulit diartikan. Dalam perangkat lunak (paket pcLasso), pengguna sendiri menetapkan nilai parameter ini, yang termasuk dalam interval [0,1], di mana 1 sesuai dengan  = 0 (laso).
= 0 (laso).
Dalam praktiknya, variasikan nilainya  = 0,25, 0,5, 0,75, 0,9, 0,95 dan 1, Anda dapat mencakup berbagai model.
= 0,25, 0,5, 0,75, 0,9, 0,95 dan 1, Anda dapat mencakup berbagai model.
Algoritma itu sendiri adalah sebagai berikut

Algoritma ini sudah ditulis dalam R, jika Anda mau, Anda sudah bisa menggunakannya. Perpustakaan itu disebut 'pcLasso'.
Jackknife Infinitesimal Tentara Swiss
Ryan Giordano (UC Berkeley); William Stephenson (MIT); Runjing Liu (UC Berkeley);
Michael Jordan (UC Berkeley); Tamara Broderick (MIT)
→ Artikel
→ Kode
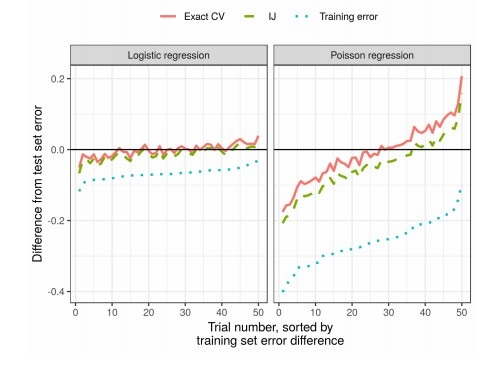
Kualitas algoritma pembelajaran mesin sering diukur dengan multi-validasi silang (cross-validation atau bootstrap). Metode ini sangat kuat, tetapi lambat pada set data besar.
Dalam pekerjaan ini, kolega menggunakan perkiraan bobot, menghasilkan hasil yang bekerja lebih cepat. Perkiraan linier ini dikenal dalam literatur statistik sebagai "pisau lipat kecil". Ini terutama digunakan sebagai alat teoritis untuk membuktikan hasil asimptotik. Hasil artikel ini berlaku terlepas dari apakah bobot dan data bersifat stokastik atau deterministik. Sebagai konsekuensinya, perkiraan ini secara berurutan memperkirakan validasi silang sebenarnya untuk setiap k tetap.
Penyajian Paper Award kepada penulis artikel

Esensi dari metode ini
Pertimbangkan masalah estimasi parameter yang tidak diketahui  dimana
dimana  Ringkas, dan ukuran dataset kami adalah
Ringkas, dan ukuran dataset kami adalah  . Analisis kami akan dilakukan pada kumpulan data tetap. Tentukan peringkat kami
. Analisis kami akan dilakukan pada kumpulan data tetap. Tentukan peringkat kami  sebagai berikut:
sebagai berikut:
- Untuk masing-masing
 diatur
diatur  (
(  ) Merupakan fungsi dari
) Merupakan fungsi dari 
 Adalah bilangan real, dan
Adalah bilangan real, dan  Merupakan vektor yang terdiri dari
Merupakan vektor yang terdiri dari 
Lalu  dapat direpresentasikan sebagai:
dapat direpresentasikan sebagai:

Memecahkan masalah optimisasi ini dengan metode gradien, kami mengasumsikan bahwa fungsinya dapat dibedakan dan kita dapat menghitung Hessian. Masalah utama yang kami selesaikan adalah biaya komputasi yang terkait dengan evaluasi ) untuk semua
untuk semua  . Kontribusi utama penulis artikel adalah menghitung estimasi
. Kontribusi utama penulis artikel adalah menghitung estimasi ) dimana
dimana ) . Dengan kata lain, optimasi kami hanya akan bergantung pada turunannya
. Dengan kata lain, optimasi kami hanya akan bergantung pada turunannya ) yang kami anggap ada dan Hessian:
yang kami anggap ada dan Hessian:
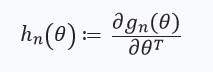
Selanjutnya, kita mendefinisikan persamaan dengan titik tetap dan turunannya:
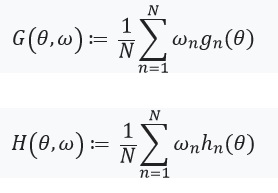
Ini ada baiknya memperhatikan itu %2Cw)%3D0) sejak itu
sejak itu ) - solusi untuk
- solusi untuk %3D0) . Kami juga mendefinisikan:
. Kami juga mendefinisikan: ) , dan matriks bobot sebagai:
, dan matriks bobot sebagai:  . Dalam hal kapan
. Dalam hal kapan  memiliki matriks terbalik, kita dapat menggunakan teorema fungsi implisit dan 'aturan rantai':
memiliki matriks terbalik, kita dapat menggunakan teorema fungsi implisit dan 'aturan rantai':
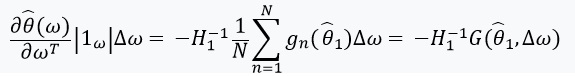
Derivatif ini memungkinkan kita untuk membentuk perkiraan linier ) melalui
melalui  yang terlihat seperti ini:
yang terlihat seperti ini:
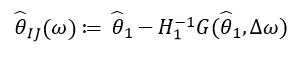
Sejak  hanya bergantung pada
hanya bergantung pada  dan
dan  , dan bukan dari solusi untuk nilai lainnya
, dan bukan dari solusi untuk nilai lainnya  , oleh karena itu, tidak perlu menghitung ulang dan menemukan nilai baru new. Sebagai gantinya, seseorang perlu menyelesaikan SLE (sistem persamaan linear).
, oleh karena itu, tidak perlu menghitung ulang dan menemukan nilai baru new. Sebagai gantinya, seseorang perlu menyelesaikan SLE (sistem persamaan linear).
Hasil
Dalam praktiknya, ini secara signifikan mengurangi waktu dibandingkan dengan validasi silang: