Jaringan saraf dan pembelajaran mendalam, bab 3, bagian 1: meningkatkan cara jaringan saraf dilatih

Ketika seseorang belajar bermain golf, ia biasanya menghabiskan sebagian besar waktunya untuk melakukan pukulan dasar. Dia kemudian mendekati pukulan lain, secara bertahap, mempelajari trik ini atau itu, berdasarkan pukulan dasar dan mengembangkannya. Demikian pula, kami sejauh ini fokus pada pemahaman algoritma backpropagation. Ini adalah "serangan dasar" kami, dasar untuk pelatihan untuk sebagian besar pekerjaan dengan jaringan saraf (NS). Dalam bab ini, saya akan berbicara tentang serangkaian teknik yang dapat digunakan untuk meningkatkan implementasi backpropagation kami yang lebih sederhana, dan untuk meningkatkan cara mengajar NS.

Di antara teknik-teknik yang akan kita pelajari dalam bab ini adalah: opsi terbaik untuk peran fungsi biaya, yaitu fungsi biaya dengan cross entropy; empat yang disebut metode regularisasi (regularisasi L1 dan L2, pengecualian neuron [putus], ekstensi buatan data pelatihan), yang meningkatkan generalisasi NS kami di luar batas data pelatihan; metode terbaik untuk menginisialisasi bobot jaringan; seperangkat metode heuristik untuk membantu Anda memilih hyperparameter yang baik untuk jaringan. Saya juga akan mempertimbangkan beberapa teknik lain, sedikit lebih dangkal. Sebagian besar, diskusi ini independen satu sama lain, sehingga Anda dapat melompati mereka jika Anda mau. Kami juga menerapkan banyak teknologi dalam kode kerja dan menggunakannya untuk meningkatkan hasil yang diperoleh untuk tugas mengklasifikasikan angka tulisan tangan, yang dipelajari pada Bab 1.

Tentu saja, kami hanya mempertimbangkan sebagian kecil dari sejumlah besar teknik yang dikembangkan untuk digunakan dengan jaringan saraf. Intinya adalah bahwa cara terbaik untuk memasuki dunia kelimpahan teknik yang tersedia adalah dengan mempelajari secara rinci beberapa yang paling penting. Menguasai teknik-teknik penting ini tidak hanya berguna dalam dirinya sendiri, itu juga akan memperdalam pemahaman Anda tentang masalah yang mungkin timbul saat menggunakan jaringan saraf. Sebagai hasilnya, Anda akan siap untuk dengan cepat mengadaptasi teknik-teknik baru sesuai kebutuhan.

Fungsi Biaya Lintas Entropi

Sebagian besar dari kita benci salah. Tak lama setelah mulai belajar piano, saya memberikan konser kecil di depan penonton. Saya gugup, dan mulai memainkan sepotong oktaf lebih rendah dari yang diperlukan. Saya bingung, dan tidak bisa melanjutkan sampai seseorang menunjukkan kesalahan kepada saya. Saya sangat malu. Namun, meskipun ini tidak menyenangkan, kami juga belajar dengan sangat cepat, memutuskan bahwa kami salah. Dan tentu saja lain kali saya berbicara kepada hadirin, saya bermain di oktaf yang tepat! Sebaliknya, kita belajar lebih lambat ketika kesalahan kita tidak didefinisikan dengan baik.

Idealnya, kami berharap jaringan saraf kami belajar dengan cepat dari kesalahan mereka. Apakah ini terjadi dalam praktek? Untuk menjawab pertanyaan ini, mari kita lihat contoh yang dibuat-buat. Ini melibatkan neuron dengan hanya satu input:



Kami mengajarkan neuron ini untuk melakukan sesuatu yang sangat sederhana: menerima 1 dan memberi 0. Tentu saja, kami bisa menemukan solusi untuk masalah sepele seperti itu dengan memilih berat dan offset secara manual, tanpa menggunakan algoritma pelatihan. Namun, akan sangat berguna untuk mencoba menggunakan gradient descent untuk mendapatkan berat dan perpindahan sebagai hasil dari pelatihan. Mari kita lihat bagaimana neuron dilatih.

Untuk kepastian, saya akan memilih bobot awal 0,6 dan offset awal 0,9. Ini adalah beberapa nilai umum yang ditetapkan sebagai titik awal, dan saya tidak memilihnya secara khusus. Awalnya, output neuron menghasilkan 0,82, jadi kita perlu belajar banyak untuk mendekati output yang diinginkan yaitu 0,0. Artikel asli memiliki bentuk interaktif di mana Anda dapat mengklik "Jalankan" dan amati proses pembelajaran. Animasi ini tidak direkam sebelumnya, browser sebenarnya menghitung gradien, dan kemudian menggunakannya untuk memperbarui bobot dan mengimbangi, dan menunjukkan hasilnya. Kecepatan belajar adalah η = 0,15, cukup lambat untuk dapat melihat apa yang terjadi, tetapi cukup cepat untuk pembelajaran berlangsung dalam hitungan detik. Fungsi biaya C adalah kuadratik, diperkenalkan pada bab pertama. Saya akan segera mengingatkan Anda tentang bentuknya yang tepat, jadi tidak perlu kembali dan mencari-cari di sana. Pelatihan dapat dimulai beberapa kali hanya dengan mengklik tombol “Jalankan”.

Seperti yang Anda lihat, neuron dengan cepat mempelajari berat dan bias, yang menurunkan biaya, dan memberikan hasil 0,09. Ini bukan hasil yang diinginkan dari 0,0, tetapi cukup baik. Misalkan kita memilih bobot awal dan offset 2.0 sebagai gantinya. Dalam hal ini, output awal akan menjadi 0,98, yang sepenuhnya salah. Mari kita lihat bagaimana dalam hal ini neuron akan belajar menghasilkan 0.

Meskipun contoh ini menggunakan tingkat belajar yang sama (η = 0,15), kita melihat bahwa belajar lebih lambat. Sekitar 150 dari zaman pertama, bobot dan perpindahan hampir tidak berubah. Kemudian pelatihan dipercepat, dan, hampir seperti pada contoh pertama, neuron bergerak cepat ke 0,0. perilaku ini aneh, tidak seperti belajar seseorang. Seperti yang saya katakan di awal, kita sering belajar paling cepat ketika kita sangat keliru. Tetapi kami hanya melihat bagaimana neuron buatan kami belajar dengan susah payah, membuat banyak kesalahan - jauh lebih sulit daripada ketika dia membuat sedikit kesalahan. Selain itu, ternyata perilaku seperti itu muncul tidak hanya dalam contoh sederhana kami, tetapi juga dalam NS tujuan yang lebih umum. Mengapa belajar sangat lambat? Bisakah saya menemukan cara untuk menghindari masalah ini?

Untuk memahami sumber masalah, kita ingat bahwa neuron kita belajar melalui perubahan berat dan perpindahan pada tingkat yang ditentukan oleh turunan parsial dari fungsi biaya, ∂C / ∂w dan ∂C / ∂b. Jadi mengatakan "belajar itu lambat" sama dengan mengatakan bahwa turunan parsial ini kecil. Masalahnya adalah untuk memahami mengapa mereka kecil. Untuk melakukan ini, mari kita hitung turunan parsial. Ingatlah bahwa kita menggunakan fungsi biaya kuadratik, yang diberikan oleh persamaan (6):

$$

$$C = \ frac {(y-a) ^ 2} {2} \ tag {54}$$

di mana a adalah output neuron ketika x = 1 digunakan pada input, dan y = 0 adalah output yang diinginkan. Untuk menulis ini secara langsung melalui bobot dan perpindahan, ingat bahwa a = σ (z), di mana z = wx + b. Menggunakan aturan rantai untuk diferensiasi berdasarkan berat dan perpindahan, kami memperoleh:

$$

$$\ frac {\ partial C} {\ partial w} = (a-y) \ sigma '(z) x = a \ sigma' (z) \ tag {55}$$

$$

$$\ frac {\ partial C} {\ partial b} = (a-y) \ sigma '(z) = a \ sigma' (z) \ tag {56}$$

di mana saya mengganti x = 1 dan y = 0. Untuk memahami perilaku ungkapan-ungkapan ini, mari kita melihat lebih dekat pada istilah σ '(z) di sebelah kanan. Ingat bentuk sigmoid:



Grafik menunjukkan bahwa ketika output neuron mendekati 1, kurva menjadi sangat datar, dan σ '(z) menjadi kecil. Persamaan (55) dan (56) memberi tahu kami bahwa ∂C / ∂w dan ∂C / ∂b menjadi sangat kecil. Karena itu perlambatan dalam belajar. Selain itu, seperti yang akan kita lihat nanti, perlambatan pelatihan terjadi, pada kenyataannya, untuk alasan yang sama dan di Majelis Nasional yang bersifat lebih umum, dan tidak hanya dalam contoh sederhana kami.

Memperkenalkan Fungsi Biaya Lintas Entropi

Apa yang kita lakukan dengan memperlambat belajar? Ternyata kita bisa menyelesaikan masalah dengan mengganti fungsi kuadrat nilai dengan fungsi nilai lainnya, yang dikenal sebagai cross-entropy. Untuk memahami lintas entropi, kami beralih dari model paling sederhana kami. Misalkan kita melatih neuron dengan beberapa nilai input x ₁ , x ₂ , ... bobot yang sesuai w ₁ , w ₂ , ... dan offset b:



Output dari neuron, tentu saja, akan menjadi a = σ (z), di mana z = wjwjxj + b adalah jumlah input yang tertimbang. Kami mendefinisikan fungsi biaya lintas-entropi untuk neuron yang diberikan sebagai

$$

$$C = - \ frac {1} {n} \ sum_x \ kiri [y \ ln a + (1-y) \ ln (1-a) \ kanan] \ tag {57}$$

di mana n adalah jumlah total unit data pelatihan, penjumlahannya mencakup semua data pelatihan x, dan y adalah hasil yang diinginkan.

Tidak jelas bahwa persamaan (57) memecahkan masalah memperlambat belajar. Jujur saja, bahkan tidak jelas masuk akal untuk menyebutnya sebagai fungsi nilai! Sebelum beralih ke perlambatan dalam pembelajaran, mari kita lihat dalam arti apa cross-entropy dapat diartikan sebagai fungsi nilai.

Dua sifat khususnya membuatnya masuk akal untuk menginterpretasikan cross-entropy sebagai fungsi nilai. Pertama, lebih besar dari nol, yaitu, C> 0. Untuk melihat ini, perhatikan bahwa (a) semua anggota individu dari jumlah dalam (57) adalah negatif, karena kedua logaritma diambil dari angka dalam kisaran dari 0 hingga 1, dan (b) tanda minus ada di depan jumlah tersebut.

Kedua, jika output nyata dari neuron dekat dengan output yang diinginkan untuk semua input pelatihan x, maka entropi silang akan mendekati nol. Untuk membuktikan ini, kita perlu mengasumsikan bahwa output y yang diinginkan adalah 0 atau 1. Biasanya ini terjadi ketika menyelesaikan masalah klasifikasi, atau menghitung fungsi Boolean. Untuk memahami apa yang terjadi jika Anda tidak membuat asumsi seperti itu, lihat latihan di bagian akhir.

Untuk membuktikan ini, bayangkan y = 0 dan ≈0 untuk beberapa input x. Jadi itu akan terjadi ketika neuron menangani input seperti itu dengan baik. Kita melihat bahwa ungkapan pertama (57) untuk nilai menghilang, karena y = 0, dan yang kedua adalah −ln (1 - a) ≈0. Hal yang sama berlaku ketika y = 1 dan a≈1. Oleh karena itu, kontribusi nilai akan kecil jika output riil mendekati yang diinginkan.

Kesimpulannya, kita mendapatkan bahwa entropi silang adalah positif, dan cenderung nol ketika neuron lebih baik menghitung output y yang diinginkan untuk semua input pelatihan x. Kami mengharapkan keberadaan kedua properti dalam fungsi biaya. Dan memang, kedua properti ini dipenuhi oleh nilai kuadratik. Karena itu, untuk lintas-entropi adalah berita baik. Namun, fungsi biaya lintas-entropi memiliki keuntungan karena, tidak seperti nilai kuadrat, ia menghindari masalah memperlambat belajar. Untuk melihat ini, mari kita hitung turunan parsial dari nilai dengan entropi silang berdasarkan berat. Ganti a = σ (z) di (57), terapkan aturan rantai dua kali, dan dapatkan

$$

$$\ frac {\ partial C} {\ partial w_j} = - \ frac {1} {n} \ sum_x \ kiri (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ kanan) \ frac {\ partial \ sigma} {\ partial w_j} \ tag {58}$$

$$

$$= - \ frac {1} {n} \ sum_x \ kiri (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ kanan) \ sigma '(z) x_j \ tag {59}$$

Mengurangi ke penyebut umum dan menyederhanakan, kita mendapatkan:

$$

$$\ frac {\ partial C} {\ partial w_j} = \ frac {1} {n} \ sum_x \ frac {\ sigma '(z) x_j} {\ sigma (z) (1- \ sigma (z)) } (\ sigma (z) -y). \ tag {60}$$

Menggunakan definisi sigmoid, σ (z) = 1 / (1 + e ^−z ) dan sedikit aljabar, kita dapat menunjukkan bahwa σ ′ (z) = σ (z) = σ (z) (1 - σ (z)). Saya akan meminta Anda untuk memverifikasi ini dalam latihan lebih lanjut, tetapi untuk sekarang, terimalah itu sebagai kebenaran. Istilah σ (z) dan σ (z) (1 - σ (z)) dibatalkan, dan ini menyebabkan

$$

$$\ frac {\ partial C} {\ partial w_j} = \ frac {1} {n} \ sum_x x_j (\ sigma (z) -y). \ tag {61}$$

Ekspresi yang bagus. Ini mengikuti dari ini bahwa kecepatan pelatihan bobot dikontrol oleh σ (z) −y, yaitu dengan kesalahan pada output. Semakin besar kesalahan, semakin cepat neuron belajar. Ini bisa diharapkan secara intuitif. Opsi ini menghindari perlambatan dalam pembelajaran yang disebabkan oleh istilah σ '(z) dalam persamaan biaya kuadratik yang serupa (55). Ketika kita menggunakan cross entropy, istilah σ '(z) berkurang dan kita tidak perlu lagi khawatir dengan ukurannya yang kecil. Pengurangan ini adalah keajaiban khusus yang dijamin oleh fungsi biaya lintas-entropi. Sebenarnya, tentu saja, ini bukan keajaiban. Seperti yang akan kita lihat nanti, cross entropy dipilih secara khusus untuk properti ini.

Demikian pula, turunan parsial untuk bias dapat dihitung. Saya tidak akan memberikan semua detail lagi, tetapi Anda dapat dengan mudah memeriksanya

$$

$$\ frac {\ partial C} {\ partial b} = \ frac {1} {n} \ sum_x (\ sigma (z) -y). \ tag {62}$$

Ini lagi membantu untuk menghindari belajar retardasi karena istilah σ '(z) dalam persamaan yang sama untuk nilai kuadratik (56).

Latihan

• Periksa bahwa σ ′ (z) = σ (z) (1 - σ (z)).

Mari kita kembali ke contoh kita yang telah kita mainkan sebelumnya dan lihat apa yang terjadi jika kita menggunakan cross entropy alih-alih nilai kuadratik. Untuk mendengarkan, kita mulai dengan kasus di mana biaya kuadrat bekerja dengan sempurna ketika bobot awal 0,6 dan offsetnya 0,9. Artikel asli memiliki bentuk interaktif di mana Anda dapat mengklik tombol Run dan melihat apa yang terjadi ketika Anda mengganti nilai kuadratik dengan cross entropy.

Tidak mengherankan, neuron dalam hal ini dilatih dengan sempurna, seperti sebelumnya. Sekarang mari kita lihat kasus di mana neuron digunakan untuk macet , dengan berat dan perpindahan mulai dari 2,0.



Sukses! Kali ini neuron belajar dengan cepat, seperti yang kita inginkan. Jika Anda melihat lebih dekat, Anda dapat melihat bahwa kemiringan kurva biaya awalnya lebih curam dibandingkan dengan daerah datar dari kurva nilai kuadratik yang sesuai. Entropi lintas-negara ini memberi kita kesejukan ini, dan itu tidak membuat kita terjebak di mana kita mengharapkan pelatihan neuron tercepat ketika dimulai dengan kesalahan yang sangat besar.

Saya tidak mengatakan kecepatan pelatihan apa yang digunakan dalam contoh terakhir. Sebelumnya, dengan nilai kuadratik, kami menggunakan η = 0,15. Haruskah kita menggunakan kecepatan yang sama dalam contoh-contoh baru? Bahkan, mengubah fungsi biaya, tidak mungkin untuk mengatakan dengan tepat apa artinya menggunakan kecepatan belajar yang “sama”; itu akan menjadi perbandingan apel dengan jeruk. Untuk kedua fungsi biaya, saya bereksperimen dengan mencari kecepatan belajar yang memungkinkan saya untuk melihat apa yang terjadi. Jika Anda masih tertarik, maka pada contoh-contoh terbaru, η = 0,005.

Anda mungkin berpendapat bahwa mengubah kecepatan belajar membuat grafik menjadi tidak berarti. Siapa yang peduli seberapa cepat neuron belajar jika kita dapat secara acak memilih kecepatan belajar? Namun keberatan ini tidak memperhitungkan poin utama. Arti dari grafik bukanlah dalam kecepatan absolut belajar, tetapi dalam bagaimana kecepatan ini berubah. Saat menggunakan fungsi kuadrat, pelatihan lebih lambat jika neuron sangat salah, dan kemudian berjalan lebih cepat ketika neuron mendekati jawaban yang diinginkan. Dengan cross-entropy, belajar lebih cepat ketika neuron membuat kesalahan besar. Dan pernyataan ini tidak tergantung pada kecepatan belajar yang diberikan.

Kami memeriksa cross entropy untuk satu neuron. Namun, ini mudah digeneralisasi ke jaringan dengan banyak lapisan dan banyak neuron. Misalkan y = y ₁ , y ₂ , ... adalah nilai yang diinginkan dari neuron keluaran, yaitu neuron pada lapisan terakhir, dan ^L1 , a ^L ₂ , ... adalah nilai output itu sendiri. Kemudian cross entropy dapat didefinisikan sebagai:

$$

$$C = - \ frac {1} {n} \ sum_x \ sum_j \ kiri [y_j \ ln a ^ L_j + (1-y_j) \ ln (1-a ^ L_j) \ kanan] \ tag {63}$$

Ini sama dengan persamaan (57), hanya sekarang sum _j jumlah kita atas semua neuron keluaran. Saya tidak akan menganalisis turunan secara detail, tetapi masuk akal untuk mengasumsikan bahwa menggunakan ekspresi (63) kita dapat menghindari perlambatan dalam jaringan dengan banyak neuron. Jika tertarik, Anda bisa mengambil turunannya pada masalah di bawah ini.

Kebetulan, istilah "cross entropy" yang saya gunakan membingungkan beberapa pembaca awal buku karena bertentangan dengan sumber lain. Secara khusus, seringkali cross entropy ditentukan untuk dua distribusi probabilitas, pj
dan qj, sebagai jp _j lnq _j . Definisi ini dapat dikaitkan dengan (57), jika satu neuron sigmoid dianggap memberikan distribusi probabilitas yang terdiri dari aktivasi neuron a dan 1-nilai yang saling melengkapi.

Namun, jika kita memiliki banyak neuron sigmoid di lapisan terakhir, vektor dan biasanya tidak memberikan distribusi probabilitas. Akibatnya, definisi tipe jp _j lnq _j tidak _ada artinya, karena kami tidak bekerja dengan distribusi probabilitas. Alih-alih (63), orang dapat membayangkan bagaimana kumpulan entropi silang yang dirangkum dari setiap neuron dirangkum, di mana aktivasi setiap neuron ditafsirkan sebagai bagian dari distribusi probabilitas dua elemen (tentu saja, tidak ada elemen probabilitas dalam jaringan kami, jadi ini sebenarnya bukan probabilitas). Dalam hal ini, (63) akan menjadi generalisasi lintas entropi untuk distribusi probabilitas.

Kapan menggunakan cross entropy alih-alih nilai kuadratik? Bahkan, cross entropy hampir selalu akan digunakan lebih baik jika Anda memiliki neuron output sigmoid. Untuk memahami hal ini, ingatlah bahwa ketika mengatur jaringan, kami biasanya menginisialisasi bobot dan offset menggunakan proses acak. Bisa terjadi bahwa pilihan ini mengarah pada fakta bahwa jaringan akan sepenuhnya salah mengartikan beberapa data input pelatihan - misalnya, output neuron akan cenderung ke 1, ketika harus pergi ke 0, atau sebaliknya. Jika kita menggunakan nilai kuadratik yang memperlambat pelatihan, itu tidak akan menghentikan pelatihan sama sekali, karena bobot akan terus dilatih pada contoh pelatihan lainnya, tetapi situasi ini jelas tidak diinginkan.

Latihan

• Satu tangkapan lintas-entropi adalah bahwa pada awalnya bisa sulit untuk mengingat peran yang sesuai dari y dan a. Sangat mudah untuk bingung, karena akan benar, - [ylna + (1 - y) ln (1 - a)] atau - [alny + (1 - a) ln (1 - y)]. Apa yang akan terjadi pada ekspresi kedua ketika y = 0 atau 1? Apakah masalah ini memengaruhi ekspresi pertama? Mengapa
• Dalam diskusi tentang neuron tunggal pada awal bagian, saya mengatakan bahwa cross entropy kecil jika σ (z) fory untuk semua data input pelatihan. , y 0 1. , (, ) y 0 1. , , σ(z)=y . ,

  $$

  $$C = -\frac{1}{n} \sum_x [y \ln y+(1-y) \ln(1-y)] \tag{64}$$
  . −[ylny+(1−y)ln(1−y)] .

• . ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \sigma'(z^L_j) \tag{65}$$
  σ'(z ^L _j ) , . , δ ^L x

  $$

  $$\delta^L = a^L-y \tag{66}$$
  , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{67}$$
  σ'(z ^L _j ) , , , . . , .
• . , . , , , , a ^L _j = z ^L _j . , δL x

  $$

  $$\delta^L = a^L-y \tag{68}$$
  , , , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{69}$$

  $$

  $$\frac{\partial C}{\partial b^L_{j}} = \frac{1}{n} \sum_x (a^L_j-y_j) \tag{70}$$
  , , . .

MNIST

Cross entropy mudah diterapkan sebagai bagian dari program yang mengajarkan jaringan menggunakan gradient descent dan back propagation. Kami akan melakukan ini nanti dengan mengembangkan versi yang lebih baik dari program klasifikasi numerik tulisan tangan awal kami dari MNIST, network.py. Program baru ini disebut network2.py, dan tidak hanya mencakup cross entropy, tetapi juga beberapa teknik lain yang dikembangkan dalam bab ini. Sementara itu, mari kita lihat seberapa baik program baru kami mengklasifikasikan digit MNIST. Seperti pada Bab 1, kita akan menggunakan jaringan dengan 30 neuron tersembunyi, dan paket mini ukuran 10. Kita akan mengatur kecepatan belajar η = 0,5 dan kita akan belajar 30 era.

Seperti yang sudah saya katakan, tidak mungkin untuk mengatakan dengan tepat kecepatan pelatihan apa yang cocok dalam hal ini, jadi saya bereksperimen dengan seleksi. Benar, ada cara yang secara kasar menghubungkan antara tingkat pembelajaran dengan nilai entropi dan kuadratik. Kami melihat sebelumnya bahwa dalam hal gradien untuk nilai kuadrat ada istilah tambahan σ '= σ (1-σ). Misalkan kita meratakan nilai-nilai ini untuk σ, ∫ ¹ ₀ dσ σ (1 - σ) = 1/6. Dapat dilihat bahwa (sangat kasar) biaya kuadrat rata-rata belajar 6 kali lebih lambat untuk tingkat belajar yang sama. Ini menunjukkan bahwa titik awal yang baik adalah dengan membagi kecepatan belajar untuk fungsi kuadratik dengan 6. Tentu saja, ini sama sekali bukan argumen yang ketat, dan Anda tidak harus menganggapnya terlalu serius. Tetapi kadang-kadang bisa bermanfaat sebagai titik awal.

Antarmuka untuk network2.py sedikit berbeda dari network.py, tetapi masih harus jelas apa yang terjadi. Dokumentasi pada network2.py dapat diperoleh dengan menggunakan perintah bantuan (network2.Network.SGD) di shell python.

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True) 

Perhatikan, omong-omong, bahwa perintah net.large_weight_initializer () digunakan untuk menginisialisasi bobot dan offset dengan cara yang sama seperti yang dijelaskan pada bab 1. Kita perlu menjalankannya karena kita akan mengubah inisialisasi bobot secara default nanti. Hasilnya, setelah memulai semua perintah di atas, kami mendapatkan jaringan yang berfungsi dengan akurasi 95,49%. Ini sangat dekat dengan hasil dari bab pertama, 95,42%, menggunakan nilai kuadratik.

Mari kita juga melihat kasus di mana kita menggunakan 100 neuron tersembunyi dan lintas entropi, dan biarkan sisanya tetap sama. Dalam hal ini, akurasinya adalah 96,82%. Ini adalah peningkatan besar atas hasil dari bab pertama, di mana kami mencapai akurasi 96,59% menggunakan nilai kuadratik. Perubahan mungkin tampak kecil, tetapi berpikir bahwa kesalahannya turun dari 3,41% menjadi 3,18%. Artinya, kami telah menghilangkan sekitar 1/14 kesalahan. Ini cukup bagus.

Cukup bagus bahwa fungsi biaya lintas-entropi memberi kami hasil yang sama atau lebih baik dibandingkan dengan nilai kuadratik. Namun, mereka tidak secara tegas membuktikan bahwa entropi silang adalah pilihan terbaik. Faktanya adalah bahwa saya tidak mencoba memilih hyperparameters sama sekali - kecepatan pelatihan, ukuran paket mini, dll. Untuk membuat peningkatan lebih meyakinkan, kita perlu menangani optimasi mereka dengan benar. Tetapi hasilnya masih inspirasional, dan perhitungan teoritis kami mengkonfirmasi bahwa cross entropy adalah pilihan yang lebih baik daripada fungsi biaya kuadratik.

Dalam nada ini, seluruh bab ini dan, pada prinsipnya, sisa buku ini akan melewati. Kami akan mengembangkan teknologi baru, mengujinya, dan mendapatkan "hasil yang lebih baik." Tentu saja, ada baiknya kita melihat peningkatan ini. Tetapi menafsirkannya selalu sulit. Ini hanya akan meyakinkan jika kita melihat peningkatan setelah bekerja serius untuk mengoptimalkan semua hyperparameter lainnya. Dan ini adalah pekerjaan yang agak rumit, membutuhkan sumber daya komputasi yang besar, dan biasanya kita tidak akan berurusan dengan investigasi yang menyeluruh. Sebagai gantinya, kami akan melangkah lebih jauh berdasarkan tes informal, seperti yang tercantum di atas. Tetapi Anda harus ingat bahwa tes semacam itu bukan bukti yang tidak ambigu, dan hati-hati memonitor kasus-kasus ketika argumen mulai gagal.

Sejauh ini, kami telah membahas cross entropy secara rinci. Mengapa membuang begitu banyak usaha jika memberikan perbaikan kecil dalam hasil MNIST kami? Nanti dalam bab ini kita akan melihat teknik lain - khususnya, regularisasi - yang memberikan perbaikan lebih kuat. Jadi mengapa kita fokus pada cross entropy? Secara khusus, karena cross entropy adalah fungsi nilai yang sering digunakan, sehingga sangat layak untuk dipahami. Tetapi alasan yang lebih penting adalah bahwa kejenuhan neuron merupakan masalah penting di bidang jaringan saraf, yang akan terus kita kembalikan ke seluruh buku. Oleh karena itu, saya membahas cross entropy dengan sangat rinci, karena ini adalah laboratorium yang baik untuk mulai memahami kejenuhan neuron dan bagaimana cara pendekatan pendekatan untuk masalah ini.

Apa arti cross entropy? Dari mana asalnya?

Diskusi kami tentang cross entropy berkisar pada analisis aljabar dan implementasi praktis. Ini berguna, tetapi sebagai hasilnya, pertanyaan konseptual yang lebih luas tetap tidak terjawab, misalnya: apa artinya lintas entropi? Apakah ada cara intuitif untuk menyajikannya? Bagaimana mungkin orang bisa membuat entropi silang?

Mari kita mulai dengan yang terakhir: apa yang bisa membuat kita berpikir tentang cross entropy? Misalkan kita menemukan perlambatan belajar yang dijelaskan sebelumnya dan menyadari bahwa itu disebabkan oleh istilah σ '(z) dalam persamaan (55) dan (56). Melihat sekilas persamaan-persamaan ini, kita bisa memikirkan apakah mungkin untuk memilih fungsi biaya sedemikian rupa sehingga istilah σ '(z) menghilang. Maka biaya C = C _{x dari} satu contoh pelatihan akan memenuhi persamaan:

$$

$$\ frac {\ partial C} {\ partial w_j} = x_j (a-y) \ tag {71}$$

$$

$$\ frac {\ partial C} {\ partial b} = (a-y) \ tag {72}$$

Jika kita memilih fungsi biaya yang membuatnya benar, mereka akan lebih mudah menggambarkan pemahaman intuitif bahwa semakin besar kesalahan awal, semakin cepat neuron belajar. Mereka juga akan memperbaiki masalah perlambatan. Sebenarnya, dimulai dengan persamaan ini, kami akan menunjukkan bahwa adalah mungkin untuk mendapatkan bentuk entropi silang dengan hanya mengikuti naluri matematika. Untuk melihat ini, kami mencatat bahwa, berdasarkan aturan rantai, kami mendapatkan:

$$

$$\ frac {\ partial C} {\ partial b} = \ frac {\ partial C} {\ partial a} \ sigma '(z) \ tag {73}$$

Menggunakan dalam persamaan terakhir σ ′ (z) = σ (z) (1 - σ (z)) = a (1 - a), kita memperoleh:

$$

$$\ frac {\ partial C} {\ partial b} = \ frac {\ partial C} {\ partial a} a (1-a) \ tag {74}$$

Dibandingkan dengan persamaan (72), kita memperoleh:

$$

$$\ frac {\ partial C} {\ partial a} = \ frac {a-y} {a (1-a)} \ tag {75}$$

Mengintegrasikan ungkapan ini di atas, kita mendapatkan:

$$

$$C = - [y \ ln a + (1-y) \ ln (1-a)] + {\ rm constant} \ tag {76}$$

Ini adalah kontribusi dari contoh pelatihan terpisah x pada fungsi biaya. Untuk mendapatkan fungsi biaya penuh, kita perlu rata-rata semua contoh pelatihan, dan kita datang ke:

$$

$$C = - \ frac {1} {n} \ sum_x [y \ ln a + (1-y) \ ln (1-a)] + {\ rm constant} \ tag {77}$$

Konstanta di sini adalah rata-rata konstanta individu dari masing-masing contoh pelatihan. Seperti yang Anda lihat, persamaan (71) dan (72) secara unik menentukan bentuk entropi silang, daging hingga konstanta yang sama. Entropi silang tidak secara ajaib dikeluarkan dari udara tipis. Dia dapat ditemukan dengan cara yang sederhana dan alami.

Bagaimana dengan ide intuitif entropi silang? Bagaimana kita membayangkannya? Penjelasan rinci akan menuntun kita untuk mengambil alih kursus pelatihan kita. Namun, kita dapat menyebutkan keberadaan cara standar menafsirkan lintas entropi, yang berasal dari bidang teori informasi. Secara kasar, cross entropy adalah ukuran kejutan. Sebagai contoh, neuron kita sedang mencoba menghitung fungsi x → y = y (x). Tetapi sebaliknya, ia menghitung fungsi x → a = a (x). Misalkan kita membayangkan sebagai estimasi neuron tentang probabilitas bahwa y = 1, dan 1-a adalah probabilitas bahwa nilai yang benar untuk y adalah 0. Kemudian lintas entropi mengukur seberapa banyak kita "terkejut" secara rata-rata ketika temukan nilai sebenarnya dari y. Kami tidak terlalu terkejut jika kami mengharapkan jalan keluar, dan kami sangat terkejut jika jalan keluarnya tidak terduga. Tentu saja, saya tidak memberikan definisi yang tegas tentang "kejutan", jadi semua ini bisa tampak seperti kata-kata kosong. Namun pada kenyataannya, dalam teori informasi ada cara yang tepat untuk menentukan hal yang tidak terduga. Sayangnya, saya tidak mengetahui contoh diskusi yang baik, singkat dan mandiri tentang hal ini di Internet. Tetapi jika Anda tertarik untuk menggali sedikit lebih dalam, maka artikel Wikipedia memiliki informasi umum yang baik yang akan mengirim Anda ke arah yang benar. Rinciannya dapat ditemukan di Bab 5 tentang ketidaksetaraan Kraft dalam sebuah buku tentang teori informasi .

Tantangan

• Kami telah membahas secara rinci perlambatan dalam pembelajaran yang dapat terjadi ketika neuron jenuh dalam jaringan menggunakan fungsi biaya kuadratik dalam pembelajaran. Faktor lain yang dapat menghambat pembelajaran adalah keberadaan istilah x _j dalam persamaan (61). Karena itu, ketika output x _j mendekati nol, bobot yang sesuai _wj akan dilatih secara perlahan. Jelaskan mengapa tidak mungkin untuk menghilangkan istilah _{xj dengan} memilih beberapa fungsi biaya yang cerdik.

Softmax (fungsi maksimum lunak)

Dalam bab ini, kita sebagian besar akan menggunakan fungsi biaya lintas-entropi untuk menyelesaikan masalah memperlambat pembelajaran. Namun, saya ingin membahas secara singkat pendekatan lain untuk masalah ini, berdasarkan apa yang disebut lapisan softmax neuron. Kami tidak akan menggunakan lapisan Softmax untuk sisa bab ini, jadi jika Anda sedang terburu-buru, Anda dapat melewati bagian ini. Namun, Softmax masih layak dipahami, khususnya karena menarik dalam dirinya sendiri, dan khususnya karena kita akan menggunakan lapisan Softmax di Bab 6, dalam diskusi kita tentang jaringan saraf yang dalam.

Gagasan Softmax adalah untuk menentukan tipe baru dari lapisan keluaran untuk HC. Itu dimulai dengan cara yang sama seperti lapisan sigmoid, dengan pembentukan input tertimbang $$$z ^ L_j = \ sum_ {k} w ^ L_ {jk} a ^ {L-1} _k + b ^ L_j$ . Namun, kami tidak menggunakan sigmoid untuk mendapatkan jawaban. Pada lapisan Softmax, kami menerapkan fungsi Softmax ke z ^L _j . Menurutnya, aktivasi a ^L _{j dari} neuron output No. j sama dengan:

$$

$$a ^ L_j = \ frac {e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} \ tag {78}$$

di mana dalam penyebut kita menjumlahkan semua neuron keluaran.

Jika fungsi Softmax tidak Anda kenal, persamaan (78) akan tampak misterius bagi Anda. Sama sekali tidak jelas mengapa kita harus menggunakan fungsi seperti itu. Juga tidak jelas bahwa itu akan membantu kita memecahkan masalah memperlambat belajar. Untuk lebih memahami persamaan (78), misalkan kita memiliki jaringan dengan empat neuron keluaran dan empat input tertimbang yang sesuai, yang akan kita tunjuk sebagai z ^L ₁ , z ^L ₂ , z ^L ₃ dan z ^L ₄ . Artikel asli berisi slider penyesuaian interaktif, yang diberikan nilai yang mungkin dari input tertimbang dan jadwal aktivasi output yang sesuai. Titik awal yang baik untuk mempelajarinya adalah dengan menggunakan slider bawah untuk meningkatkan zL4.





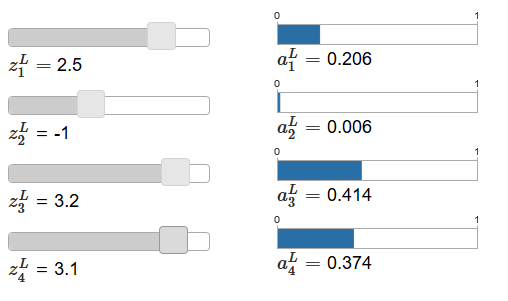
Dengan meningkatkan zL4, seseorang dapat mengamati peningkatan aktivasi output yang sesuai, sebuah ^L4 , dan penurunan aktivasi output lainnya. Dengan penurunan zL4aL4 akan berkurang, dan semua aktivasi output lainnya akan meningkat. Setelah melihat dari dekat, Anda akan melihat bahwa dalam kedua kasus, perubahan umum pada aktivasi lain justru mengimbangi perubahan yang terjadi pada ^L ₄ . Alasan untuk ini adalah jaminan bahwa semua aktivasi output total memberikan 1, yang dapat kita buktikan menggunakan persamaan (78) dan beberapa aljabar:

$$

$$\ sum_j a ^ L_j = \ frac {\ sum_j e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} = 1 \ tag {79}$$

Akibatnya, dengan peningkatan pada ^L4 _, aktivasi output yang tersisa harus berkurang dengan nilai yang sama secara total untuk memastikan bahwa jumlah semua aktivasi output sama dengan 1. Dan, tentu saja, pernyataan serupa akan berlaku untuk semua aktivasi lainnya.

Ini juga mengikuti dari persamaan (78) bahwa semua aktivasi output adalah positif, karena fungsi eksponensial adalah positif. Menggabungkan ini dengan pengamatan dari bagian sebelumnya, kami menemukan bahwa output dari lapisan Softmax adalah satu set angka positif yang memberikan total 1. Dengan kata lain, output dari lapisan Softmax dapat direpresentasikan sebagai distribusi probabilitas.

Fakta bahwa output dari lapisan Softmax adalah distribusi probabilitas sangat menyenangkan. Dalam banyak masalah, akan lebih mudah untuk dapat menginterpretasikan aktivasi output a ^L _j sebagai perkiraan oleh jaringan probabilitas bahwa bulet j akan menjadi pilihan yang benar. Jadi, misalnya, dalam masalah klasifikasi MNIST, kita dapat menginterpretasikan ^L _j sebagai estimasi jaringan dari probabilitas bahwa j akan menjadi klasifikasi angka yang benar.

Sebaliknya, jika lapisan output adalah sigmoid, maka kita pasti tidak dapat mengasumsikan bahwa aktivasi membentuk distribusi probabilitas. Saya tidak akan membuktikan ini secara ketat, tetapi masuk akal untuk mengasumsikan bahwa aktivasi lapisan sigmoid dalam kasus umum tidak membentuk distribusi probabilitas. Oleh karena itu, menggunakan lapisan keluaran sigmoid, kita tidak akan mendapatkan interpretasi sederhana dari aktivasi keluaran.

Latihan

• Buat contoh yang menunjukkan bahwa dalam jaringan dengan lapisan keluaran sigmoid, aktivasi keluaran a _Lj tidak selalu menambahkan hingga 1.

Kita mulai memahami sedikit tentang fungsi Softmax dan bagaimana lapisan Softmax berperilaku. Singkatnya: eksponen dalam persamaan (78) memastikan bahwa semua aktivasi output positif. Jumlah dalam penyebut persamaan (78) memastikan bahwa Softmax memberikan total 1. Oleh karena itu, persamaan semacam ini tidak lagi tampak misterius: ini adalah cara alami untuk memastikan bahwa aktivasi output membentuk distribusi probabilitas. Softmax dapat dibayangkan sebagai cara untuk skala z Lj dan kemudian kompres bersama untuk membentuk distribusi probabilitas.

Latihan

• Kebodohan Softmax. Tunjukkan bahwa ∂a ^L _j / ∂z ^L _k positif jika j = k, dan negatif jika j ≠ k. Sebagai hasilnya, peningkatan z ^L _j dijamin untuk meningkatkan aktivasi output yang sesuai a ^L _j , dan mengurangi semua aktivasi output lainnya. Kami telah melihat ini secara empiris menggunakan contoh slider, tetapi bukti ini akan ketat.
• Softmax Nonlocality. Fitur bagus dari lapisan sigmoid adalah bahwa output a ^L _j adalah fungsi dari input tertimbang yang sesuai, a ^L _j = σ (z ^L _j ). Jelaskan mengapa hal ini tidak terjadi pada lapisan Softmax: aktivasi output apa pun dan tergantung pada semua input tertimbang.

Tantangan

• Balikkan lapisan Softmax. Misalkan kita memiliki NS dengan lapisan Softmax keluaran dan aktivasi _yang diketahui. Tunjukkan bahwa input tertimbang yang sesuai adalah dalam bentuk z ^L _j = ln a ^L _j + C, di mana C adalah konstanta independen j.

Mempelajari masalah pelambatan

Kita telah menjadi cukup akrab dengan lapisan neuron Softmax. Namun sejauh ini kita belum melihat bagaimana lapisan Softmax memungkinkan kita untuk memecahkan masalah memperlambat belajar. Untuk memahami hal ini, mari kita mendefinisikan fungsi biaya berdasarkan "kemungkinan log". Kami akan menggunakan x untuk menunjukkan input pelatihan jaringan, dan y untuk output yang diinginkan yang sesuai. Maka LPS yang terkait dengan input pelatihan ini adalah:

$$

$$C \ equiv - \ ln a ^ L_y \ tag {80}$$

Jadi jika, misalnya, kita mempelajari gambar MNIST, dan gambar 7 dimasukkan ke dalam input, maka LPS akan menjadi aln dalam ^L ₇ . Untuk memahami ini secara intuitif, kami mempertimbangkan kasus ketika jaringan berupaya dengan baik dengan pengakuan, yaitu, yakin bahwa itu pada input 7. Dalam hal ini, ia akan mengevaluasi nilai probabilitas yang sesuai ^L ₇ mendekati 1, oleh karena itu biaya −ln ^L ₇ akan kecil . Sebaliknya, jika jaringan tidak bekerja dengan baik, maka probabilitas ^L ₇ akan lebih sedikit, dan biaya −Ln ^L ₇ akan lebih. Oleh karena itu, LPS berperilaku seperti yang diharapkan dari fungsi biaya.

Bagaimana dengan masalah perlambatan? Untuk menganalisanya, kita ingat bahwa hal utama dalam deselerasi adalah perilaku ∂C / ∂w ^L _jk dan ∂C / ∂b ^L _j . Saya tidak akan menjelaskan secara terperinci penangkapan turunan - Saya akan meminta Anda untuk melakukan ini dalam tugas, tetapi menggunakan beberapa aljabar Anda dapat menunjukkan bahwa:

$$

$$\ frac {\ partial C} {\ partial b ^ L_j} = a ^ L_j-y_j \ tag {81}$$

$$

$$\ frac {\ partial C} {\ partial w ^ L_ {jk}} = a ^ {L-1} _k (a ^ L_j-y_j) \ tag {82}$$

Saya telah bermain sedikit dengan notasi di sini, dan saya menggunakan "y" sedikit berbeda dari pada paragraf terakhir. Di sana, y menunjukkan output jaringan yang diinginkan - yaitu, jika output adalah "7", maka inputnya adalah gambar 7. Dan dalam persamaan ini, y menunjukkan vektor aktivasi output yang sesuai dengan 7, yaitu, vektor dengan semua nol kecuali kesatuan dalam 7 posisi ke-5.

Persamaan ini sama dengan ekspresi serupa yang kami peroleh dalam analisis awal entropi silang. Bandingkan, misalnya, persamaan (82) dan (67). Ini adalah persamaan yang sama, meskipun yang terakhir dirata-ratakan atas contoh pelatihan. Dan, seperti dalam kasus pertama, ungkapan-ungkapan ini menjamin bahwa pembelajaran tidak melambat. Sangat berguna untuk membayangkan bahwa lapisan keluaran Softmax dengan LPS sangat mirip dengan lapisan dengan keluaran sigmoid dan biaya berdasarkan cross entropy.

Mengingat kesamaan mereka, apa yang harus digunakan - output sigmoid dan cross entropy, atau output Softmax dan LPS? Faktanya, dalam banyak kasus kedua pendekatan bekerja dengan baik. Meskipun nanti dalam bab ini kita akan menggunakan lapisan keluaran sigmoid dengan biaya berdasarkan cross entropy. Kemudian, dalam bab 6, kadang-kadang kita akan menggunakan output Softmax dan LPS. Alasan untuk perubahan adalah untuk membuat beberapa jaringan berikut lebih mirip dengan jaringan yang ditemukan di beberapa makalah penelitian yang berpengaruh. Dari sudut pandang yang lebih umum, Softmax dan LPS harus digunakan ketika Anda perlu mengartikan aktivasi output sebagai probabilitas. Ini tidak selalu diperlukan, tetapi dapat berguna dalam masalah klasifikasi (seperti MNIST), yang mencakup kelas yang tidak berpotongan.

Tugasnya

• Turunkan persamaan (81) dan (82).
• Dari mana nama Softmax berasal? Misalkan kita mengubah fungsi Softmax sehingga aktivasi output diberikan oleh persamaan

  $$

  $$a ^ L_j = \ frac {e ^ {c z ^ L_j}} {\ sum_k e ^ {c z ^ L_k}} \ tag {83}$$
  di mana c adalah konstanta positif. Perhatikan bahwa c = 1 sesuai dengan fungsi Softmax standar. Tetapi dengan menggunakan nilai c yang berbeda, kami mendapatkan fungsi lain yang masih akan mirip secara kualitatif dengan Softmax. Tunjukkan bahwa aktivasi output membentuk distribusi probabilitas, seperti halnya dengan Softmax biasa. Misalkan kita membuat c sangat besar, yaitu, c → & inf;. Berapa nilai pembatas dari aktivasi keluaran a ^L _j ? Setelah menyelesaikan masalah ini, harus jelas mengapa fungsi dengan c = 1 dianggap sebagai "versi lunak" dari fungsi maksimum. Di sinilah istilah softmax berasal.
• Kembali propagasi dengan Softmax dan LPS. Dalam bab terakhir, kami menurunkan algoritma backpropagation untuk jaringan yang mengandung lapisan sigmoid. Untuk menerapkan algoritma ini ke jaringan dan lapisan Softmax, kita perlu menurunkan ekspresi untuk kesalahan δ ^L _j ≡ ∂C / ∂z ^L _j . Tunjukkan bahwa ungkapan yang cocok adalah

  $$

  $$\ delta ^ L_j = a ^ L_j -y_j \ tag {84}$$
  Dengan menggunakan ungkapan ini, kita dapat menerapkan algoritma backpropagation ke jaringan menggunakan lapisan Softmax keluaran dan LPS.

Pelatihan ulang dan regularisasi

Peraih Nobel Enrico Fermi pernah diminta pendapat tentang model matematika yang diusulkan oleh beberapa rekan untuk memecahkan masalah fisik penting yang belum terselesaikan. Model tersebut sangat sesuai dengan eksperimen, tetapi Fermi skeptis tentang hal itu. Dia bertanya berapa banyak parameter gratis di dalamnya yang bisa diubah. "Empat," kata mereka. Fermi menjawab: "Saya ingat bagaimana teman saya Johnny von Neumann suka mengatakan bahwa dengan empat parameter Anda dapat mendorong seekor gajah di sana, dan dengan lima Anda dapat membuatnya melambaikan belalainya."

Arti sejarah, tentu saja, adalah bahwa model dengan sejumlah besar parameter bebas dapat menggambarkan berbagai fenomena yang mengejutkan.Bahkan jika model seperti itu berfungsi baik dengan data yang tersedia, itu tidak secara otomatis menjadikannya model yang baik. Ini mungkin berarti bahwa model memiliki kebebasan yang cukup untuk menggambarkan hampir semua kumpulan data dari ukuran tertentu tanpa mengungkapkan ide utama dari fenomena tersebut. Ketika ini terjadi, model bekerja dengan baik dengan data yang ada, tetapi tidak dapat menyamaratakan situasi baru. Tes sebenarnya dari sebuah model adalah kemampuannya untuk membuat prediksi dalam situasi yang belum pernah ditemui sebelumnya.

Fermi dan von Neumann curiga pada model dengan empat parameter. NS kami dengan 30 neuron tersembunyi untuk klasifikasi angka MNIST memiliki hampir 24.000 parameter! Ini adalah beberapa parameter. NS kami dengan 100 neuron tersembunyi memiliki hampir 80.000 parameter, dan NS mendalam dalam dari parameter ini terkadang memiliki jutaan atau bahkan miliaran. Bisakah kita mempercayai hasil pekerjaan mereka?

Mari kita memperumit masalah ini dengan menciptakan situasi di mana jaringan kita secara buruk membuat generalisasi situasi baru untuknya. Kami akan menggunakan NS dengan 30 neuron tersembunyi dan 23.860 parameter. Tapi kami tidak akan melatih jaringan dengan semua 50.000 gambar MNIST. Sebagai gantinya, kami hanya menggunakan 1000 yang pertama. Menggunakan set terbatas akan membuat masalah generalisasi lebih jelas. Kami akan belajar seperti sebelumnya, menggunakan fungsi biaya berdasarkan cross-entropy, dengan kecepatan belajar η = 0,5 dan ukuran paket mini 10. Namun, kami akan mempelajari 400 era, yang sedikit lebih banyak dari sebelumnya, karena ada contoh pelatihan kami tidak punya banyak. Mari kita gunakan network2 untuk melihat bagaimana perubahan fungsi biaya:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True, monitor_training_cost=True) 

Dengan menggunakan hasilnya, kita dapat membuat grafik perubahan biaya saat melatih jaringan (grafik dibuat menggunakan program overfitting.py):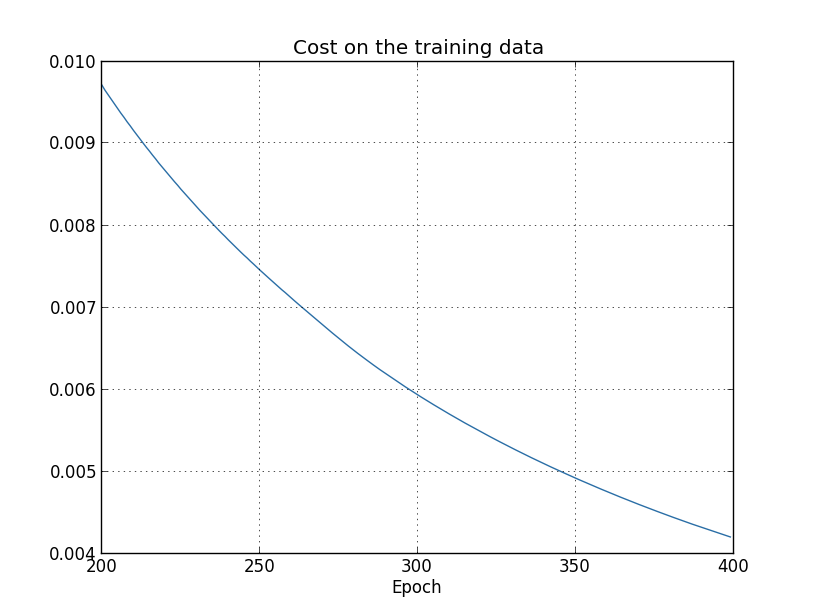



Kelihatannya menggembirakan, ada penurunan biaya yang mulus, seperti yang diharapkan. Perlu diingat bahwa saya hanya menunjukkan zaman dari 200 hingga 399. Sebagai hasilnya, kita melihat pada skala yang diperbesar tahap akhir pelatihan, di mana, seperti yang akan kita lihat nanti, semua yang paling menarik terjadi.

Sekarang mari kita lihat bagaimana akurasi klasifikasi pada data verifikasi berubah seiring waktu:



Kemudian saya kembali menambah jadwal. Dalam 200 era pertama, yang tidak terlihat di sini, akurasi meningkat hingga hampir 82%. Kemudian pelatihan lambat laun melambat. Akhirnya, sekitar era 280, akurasi klasifikasi tidak lagi membaik. Dalam era kemudian, hanya fluktuasi stokastik kecil yang diamati di sekitar nilai akurasi yang dicapai pada zaman ke-280. Bandingkan ini dengan grafik sebelumnya, di mana biaya yang terkait dengan data pelatihan berkurang secara bertahap. Jika Anda hanya mempelajari biaya ini, tampaknya model tersebut membaik. Namun, hasil kerja dengan data uji memberi tahu kami bahwa peningkatan ini hanyalah ilusi. Seperti dalam model yang tidak disukai Fermi, apa yang dipelajari jaringan kami setelah era ke-280 tidak lagi digeneralisasikan ke data verifikasi. Oleh karena itu, pelatihan ini tidak lagi berguna. Kami mengatakan bahwa setelah era ke-280, jaringan pelatihan ulang,atau overfitting.

Anda mungkin bertanya-tanya apakah bukan masalah bahwa saya sedang mempelajari biaya berdasarkan data pelatihan, dan bukan pada keakuratan klasifikasi data verifikasi. Dengan kata lain, mungkin masalahnya adalah kita membandingkan apel dengan jeruk. Apa yang akan terjadi jika kita membandingkan biaya data pelatihan dengan biaya verifikasi, yaitu, kita akan membandingkan tindakan yang sebanding? Atau mungkin kita bisa membandingkan akurasi klasifikasi data pelatihan dan tes? Bahkan, fenomena yang sama muncul terlepas dari bagaimana perbandingan itu dibuat. Namun detailnya berubah. Misalnya, mari kita lihat nilai dari data verifikasi:



Dapat dilihat bahwa biaya data verifikasi membaik hingga sekitar era ke-15, dan kemudian mulai memburuk sama sekali, meskipun biaya data pelatihan terus meningkat. Ini adalah tanda lain dari model yang dilatih ulang. Namun, muncul pertanyaan, era apa yang harus kita pertimbangkan pada titik di mana pelatihan ulang mulai berlaku selama pelatihan - 15 atau 280? Dari sudut pandang praktis, kami tetap tertarik untuk meningkatkan keakuratan klasifikasi data verifikasi, dan biaya hanyalah mediator dari keakuratan klasifikasi. Oleh karena itu, masuk akal untuk mempertimbangkan era 280 titik, setelah itu pelatihan ulang mulai menang atas pelatihan Majelis Nasional kita.

Tanda lain pelatihan ulang dapat dilihat pada keakuratan klasifikasi data pelatihan:



Akurasi tumbuh, mencapai 100%. Yaitu, jaringan kami dengan benar mengklasifikasikan semua 1000 gambar pelatihan! Sementara itu, akurasi verifikasi hanya tumbuh 82,27%. Artinya, jaringan kami hanya mempelajari fitur-fitur set pelatihan, dan tidak belajar mengenali angka sama sekali. Tampaknya jaringan hanya mengingat set pelatihan, tidak memahami angka dengan cukup baik untuk menggeneralisasikan set tes ini.

Pelatihan ulang adalah masalah serius Majelis Nasional. Ini terutama berlaku untuk NS modern, yang biasanya memiliki banyak bobot dan perpindahan. Untuk pelatihan yang efektif, kita perlu cara untuk menentukan kapan pelatihan ulang terjadi agar tidak berlatih kembali. Dan kami juga ingin mengurangi efek pelatihan ulang.

Cara yang jelas untuk mendeteksi pelatihan ulang adalah dengan menggunakan pendekatan di atas, memantau keakuratan bekerja dengan data verifikasi selama pelatihan jaringan. Jika kami melihat bahwa keakuratan pada data verifikasi tidak lagi membaik, kami harus menghentikan pelatihan. Tentu saja, secara tegas, ini tidak harus menjadi tanda pelatihan ulang. Mungkin keakuratan bekerja dengan data tes dan pelatihan akan berhenti membaik pada saat yang sama. Namun menerapkan strategi semacam itu akan mencegah pelatihan ulang.

Dan kami akan menggunakan variasi kecil dari strategi ini. Ingatlah bahwa ketika kita memuat data ke MNIST, kita membaginya menjadi tiga set:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Sejauh ini kami telah menggunakan training_data dan test_data, dan mengabaikan validation_data [konfirmasi]. Validation_data berisi 10.000 gambar, yang berbeda dari 50.000 gambar dari set pelatihan MNIST dan 10.000 gambar dari set validasi. Alih-alih menggunakan test_data untuk mencegah overfitting, kami akan menggunakan validation_data. Untuk melakukan ini, kita akan menggunakan strategi yang hampir sama dengan yang dijelaskan di atas untuk test_data. Artinya, kami akan menghitung akurasi klasifikasi validation_data pada akhir setiap era. Setelah akurasi klasifikasi validation_data penuh, kami akan berhenti belajar. Strategi ini disebut pemberhentian dini. Tentu saja, dalam praktiknya, kita tidak akan dapat segera mengetahui bahwa keakuratannya memuaskan. Sebaliknya, kami akan melanjutkan pelatihan sampai kami memastikan hal ini (dan memutuskanketika Anda perlu berhenti, itu tidak selalu mudah, dan Anda dapat menggunakan pendekatan yang lebih atau kurang agresif untuk ini).

Mengapa menggunakan validation_data untuk mencegah pelatihan ulang daripada test_data? Ini adalah bagian dari strategi yang lebih umum untuk menggunakan validation_data untuk mengevaluasi berbagai pilihan hyperparameter - jumlah zaman untuk dipelajari, kecepatan belajar, arsitektur jaringan terbaik, dll. Kami menggunakan taksiran-taksiran ini untuk menemukan dan menetapkan nilai yang baik untuk parameter yang terlalu tinggi. Dan meskipun saya belum menyebutkan ini, sebagian karena ini saya membuat pilihan hiperparameter dalam contoh sebelumnya dalam buku ini.

Tentu saja, pernyataan ini tidak menjawab pertanyaan mengapa kami menggunakan validation_data, dan bukan test_data, untuk mencegah overfitting. Itu hanya menggantikan jawaban untuk pertanyaan yang lebih umum - mengapa kita menggunakan validation_data, dan bukan test_data, untuk memilih hyperparameters? Untuk memahami hal ini, perlu diingat bahwa ketika memilih hyperparameters, kita kemungkinan besar harus memilih dari berbagai pilihan mereka. Jika kami menetapkan hyperparameters berdasarkan peringkat dari test_data, kami mungkin akan menyesuaikan data ini terlalu khusus untuk test_data. Artinya, kami mungkin menemukan hyperparameters yang cocok untuk fitur spesifik data spesifik dari test_data, namun, operasi jaringan kami tidak akan digeneralisasi ke set data lainnya. Kami menghindari ini dengan memilih hyperparameters menggunakan validation_data. Dan kemudian, setelah menerima GP yang kami butuhkan,kami melakukan penilaian akurasi akhir menggunakan test_data. Ini memberi kami keyakinan bahwa hasil kami dengan test_data adalah ukuran sebenarnya dari tingkat generalisasi NS. Dengan kata lain, data pendukung adalah data pelatihan khusus yang membantu kita mempelajari GP yang baik. Pendekatan ini untuk menemukan dokter kadang-kadang disebut metode retensi, karena validation_data "diadakan" secara terpisah dari training_data.

Dalam praktiknya, bahkan setelah mengevaluasi kualitas pekerjaan pada test_data, kami ingin mengubah pikiran kami dan mencoba pendekatan yang berbeda - mungkin arsitektur jaringan yang berbeda - yang akan mencakup pencarian kumpulan dokter baru. Dalam hal ini, apakah ada bahaya bahwa kita tidak perlu beradaptasi dengan test_data? Apakah kita memerlukan jumlah set data yang berpotensi tak terbatas sehingga kita dapat yakin bahwa hasil kita digeneralisasikan dengan baik? Secara umum, ini adalah masalah yang mendalam dan kompleks. Tetapi untuk tujuan praktis kami, kami tidak akan terlalu khawatir tentang hal ini. Kami langsung terjun ke dalam penelitian lebih lanjut menggunakan metode retensi sederhana berdasarkan training_data, validation_data, dan test_data, seperti dijelaskan di atas.

Sejauh ini, kami telah mempertimbangkan pelatihan ulang menggunakan 1000 gambar pelatihan. Apa yang terjadi jika kita menggunakan satu set pelatihan lengkap 50.000 gambar? Kami akan membiarkan semua parameter lainnya tidak berubah (30 neuron tersembunyi, kecepatan belajar 0,5, ukuran paket mini 10), tetapi kami akan mempelajari 30 era menggunakan 50.000 gambar. Berikut ini adalah grafik yang menunjukkan keakuratan klasifikasi pada data pelatihan dan data uji. Perhatikan bahwa di sini saya menggunakan data validasi daripada data validasi untuk membuatnya lebih mudah untuk membandingkan hasilnya dengan grafik sebelumnya.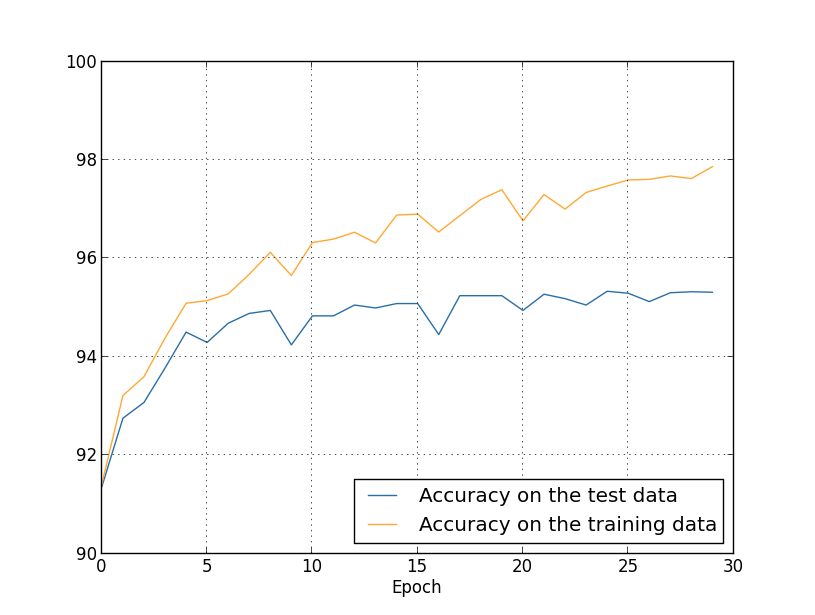



Dapat dilihat bahwa indikator akurasi pada tes dan data pelatihan tetap lebih dekat satu sama lain daripada saat menggunakan 1000 contoh pelatihan. Secara khusus, akurasi klasifikasi terbaik, 97,86%, hanya 2,53% lebih tinggi dari 95,33% dari data verifikasi. Bandingkan dengan terobosan awal 17,73%! Pelatihan ulang sedang berlangsung, tetapi sangat berkurang. Jaringan kami mengumpulkan informasi jauh lebih baik, mulai dari pelatihan hingga menguji data. Secara umum, salah satu cara terbaik untuk mengurangi pelatihan ulang adalah dengan menambah jumlah data pelatihan. Dengan data pelatihan yang cukup, sulit untuk melatih ulang bahkan jaringan yang sangat besar. Sayangnya, mendapatkan data pelatihan itu mahal dan / atau sulit, jadi opsi ini tidak selalu praktis.

Regularisasi

Meningkatkan jumlah data pelatihan adalah salah satu cara untuk mengurangi pelatihan ulang. Apakah ada cara lain untuk mengurangi pelatihan ulang? Salah satu pendekatan yang mungkin adalah mengurangi ukuran jaringan. Benar, jaringan besar memiliki potensi lebih dari yang kecil, jadi kami enggan menggunakan opsi ini.

Untungnya, ada teknik lain yang dapat mengurangi pelatihan ulang, bahkan ketika kami telah memperbaiki ukuran jaringan dan data pelatihan. Mereka dikenal sebagai teknik regularisasi. Dalam bab ini, saya akan menjelaskan salah satu teknik yang paling populer, kadang-kadang disebut bobot yang melemah, atau mengatur L2. Idenya adalah untuk menambahkan anggota tambahan yang disebut anggota regularisasi ke fungsi biaya. Inilah cross-entropy dengan regularisasi:

$$

$$C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2 \tag{85}$$

Istilah pertama adalah ungkapan umum untuk cross entropy. Tapi kami menambahkan yang kedua, yaitu, jumlah kuadrat dari semua bobot jaringan. Ini diskalakan oleh faktor λ / 2n, di mana λ> 0 adalah parameter regularisasi, dan n, seperti biasa, adalah ukuran set pelatihan. Kami akan membahas cara memilih λ. Perlu juga dicatat bahwa bias tidak termasuk dalam istilah regularisasi. Tentang itu di bawah ini.

Tentu saja, dimungkinkan untuk mengatur fungsi biaya lainnya, misalnya kuadratik. Ini dapat dilakukan dengan cara yang serupa:

$$

$$C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2 \tag{86}$$

Dalam kedua kasus, kita dapat menuliskan fungsi biaya yang diatur sebagai

$$

$$C = C_0 + \frac{\lambda}{2n} \sum_w w^2 \tag{87}$$

di mana C ₀ adalah fungsi biaya asli tanpa regularisasi.

Secara intuitif jelas bahwa titik regularisasi adalah untuk membujuk jaringan untuk memilih bobot yang lebih kecil, semua hal lain dianggap sama. Bobot besar hanya akan mungkin jika mereka secara signifikan meningkatkan bagian pertama dari fungsi biaya. Dengan kata lain, regularisasi adalah cara memilih kompromi antara menemukan bobot kecil dan meminimalkan fungsi biaya awal. Penting bahwa kedua elemen kompromi ini bergantung pada nilai λ: ketika λ kecil, kami lebih memilih untuk meminimalkan fungsi biaya asli, dan ketika λ besar, kami lebih suka bobot kecil.

Sama sekali tidak jelas mengapa pilihan kompromi semacam itu akan membantu mengurangi pelatihan ulang! Tapi ternyata itu membantu. Kami akan mencari tahu mengapa ini membantu di bagian selanjutnya. Tapi pertama-tama, mari kita bekerja dengan sebuah contoh yang menunjukkan bahwa regularisasi memang mengurangi pelatihan ulang.

Untuk membangun sebuah contoh, pertama-tama kita perlu memahami bagaimana menerapkan algoritma pelatihan dengan keturunan gradien stokastik ke NS yang diatur. Secara khusus, kita perlu tahu bagaimana menghitung turunan parsial, ∂C / ∂w dan ∂C / ∂b untuk semua bobot dan offset dalam jaringan. Setelah mengambil turunan parsial dalam persamaan (87) kita mendapatkan:

$$

$$\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{88}$$

$$

$$\frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b} \tag{89}$$

Istilah ∂C ₀ / ∂w dan ∂C ₀ / ∂w dapat dihitung melalui OP, seperti yang dijelaskan dalam bab sebelumnya. Kami melihat bahwa mudah untuk menghitung gradien dari fungsi biaya yang diatur: Anda hanya perlu menggunakan OP seperti biasa, dan kemudian menambahkan λ / nw ke turunan parsial dari semua istilah bobot. Derivatif parsial sehubungan dengan perpindahan tidak berubah, oleh karena itu, aturan pembelajaran dengan penurunan gradien untuk perpindahan tidak berbeda dari yang biasa:

$$

$$b \rightarrow b -\eta \frac{\partial C_0}{\partial b} \tag{90}$$

Aturan pelatihan untuk bobot berubah menjadi:

$$

$$w \rightarrow w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{91}$$

$$

$$= \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w} \tag{92}$$

Semuanya sama seperti pada aturan gradient descent yang biasa, kecuali bahwa kita pertama-tama mengukur skala w dengan faktor 1 - ηλ / n. Skala ini kadang-kadang disebut penurunan berat badan, karena mengurangi berat badan. Sekilas, tampaknya bobotnya cenderung tak tertahankan. Tetapi tidak demikian, karena istilah lain dapat menyebabkan peningkatan bobot jika hal ini mengarah pada penurunan fungsi biaya tidak teratur.

Ok, biarkan gradient descent bekerja seperti ini. Bagaimana dengan penurunan gradien stokastik? Nah, seperti dalam versi penurunan gradien stokastik stokastik, kita dapat memperkirakan ∂C ₀ / ∂w melalui rata-rata paket mini contoh pelatihan m. Oleh karena itu, aturan pembelajaran yang diatur untuk penurunan gradien stokastik berubah menjadi (lihat persamaan (20)):

$$

$$w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w} \tag{93}$$

di mana jumlah digunakan untuk contoh pelatihan x dalam paket mini, dan C _x adalah biaya tidak teratur untuk setiap contoh pelatihan. Semuanya sama seperti pada aturan biasa penurunan gradien stokastik, dengan pengecualian 1 - ηλ / n, faktor penurunan berat badan. Akhirnya, untuk melengkapi gambar, izinkan saya menuliskan aturan yang diatur untuk offset. Secara alami, persis sama seperti dalam kasus tidak beraturan (lihat persamaan (21)):

$$

$$b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b} \tag{94}$$

di mana jumlahnya digunakan untuk contoh pelatihan x dalam paket-mini.

Mari kita lihat bagaimana regularisasi mengubah keefektifan Majelis Nasional kita. Kami akan menggunakan jaringan dengan 30 neuron tersembunyi, paket mini ukuran 10, kecepatan belajar 0,5, dan fungsi biaya dengan cross entropy. Namun, kali ini kami menggunakan parameter regularisasi λ = 0,1. Dalam kode, saya menamai variabel ini lmbda, karena kata lambda dicadangkan dalam python untuk hal-hal yang tidak terkait dengan topik kita. Saya juga menggunakan test_data lagi bukan validation_data. Tetapi saya memutuskan untuk menggunakan test_data, karena hasilnya dapat dibandingkan secara langsung dengan hasil awal kami yang tidak teratur. Anda dapat dengan mudah mengubah kode sehingga menggunakan validation_data dan pastikan hasilnya sama.

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, ... evaluation_data=test_data, lmbda = 0.1, ... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True, ... monitor_training_cost=True, monitor_training_accuracy=True) 

Biaya data pelatihan terus menurun, seperti dalam kasus sebelumnya, tanpa regularisasi:



Tapi kali ini, akurasi pada test_data terus meningkat di seluruh 400 zaman: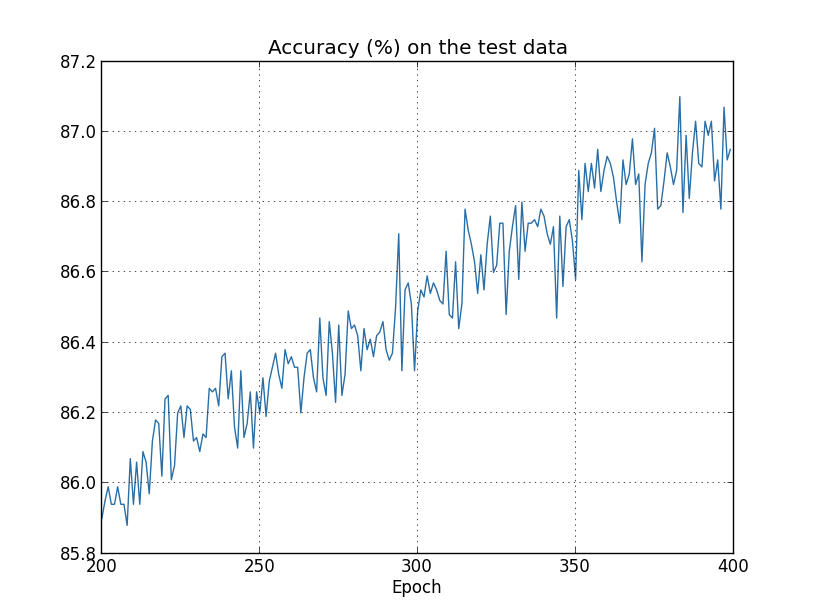



Jelas, regularisasi menekan pelatihan ulang. Selain itu, akurasi telah meningkat secara signifikan, dan akurasi klasifikasi puncak mencapai 87,1%, dibandingkan dengan puncak 82,27% yang dicapai dalam kasus tanpa regularisasi. Secara umum, kami hampir pasti mencapai hasil yang lebih baik dengan terus belajar setelah 400 era. Secara empiris, regularisasi tampaknya membuat jaringan kami lebih menggeneralisasi pengetahuan, dan secara signifikan mengurangi efek pelatihan ulang.

Apa yang terjadi jika kita meninggalkan lingkungan buatan kita, yang hanya menggunakan 1.000 gambar pengajaran, dan kembali ke set penuh 50.000 gambar? Tentu saja, kita telah melihat bahwa pelatihan ulang adalah masalah yang jauh lebih kecil dengan set lengkap 50.000 gambar. Apakah regularisasi membantu meningkatkan hasilnya? Mari kita pertahankan nilai hiperparameter sebelumnya - 30 zaman, kecepatan 0,5, ukuran paket mini 10. Namun, kita perlu mengubah parameter regularisasi. Faktanya adalah bahwa ukuran n set pelatihan melonjak dari 1000 menjadi 50.000, dan ini mengubah faktor pelemahan bobot 1 - ηλ / n. Jika kita terus menggunakan λ = 0,1, ini berarti bobot menjadi lebih lemah, dan sebagai akibatnya, efek regularisasi menurun. Kami mengimbangi ini dengan menerima λ = 5.0.

Ok, mari latih jaringan kami dengan terlebih dahulu menginisialisasi ulang bobot:

 >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, ... evaluation_data=test_data, lmbda = 5.0, ... monitor_evaluation_accuracy=True, monitor_training_accuracy=True) 

Kami mendapatkan hasilnya: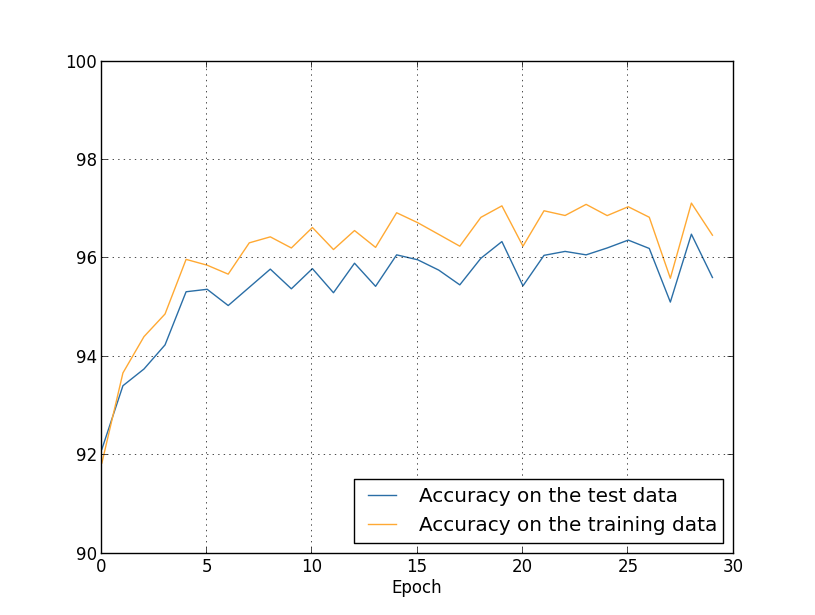



Banyak hal menyenangkan. Pertama, akurasi klasifikasi kami pada data verifikasi telah tumbuh, dari 95,49% tanpa regularisasi menjadi 96,49% dengan regularisasi. Ini merupakan peningkatan besar. Kedua, dapat dilihat bahwa kesenjangan antara hasil pekerjaan pada pelatihan dan set tes jauh lebih rendah dari sebelumnya, kurang dari 1%. Kesenjangan masih layak, tetapi kami jelas telah membuat kemajuan yang signifikan dalam mengurangi pelatihan ulang.

Akhirnya, lihat akurasi klasifikasi apa yang kita dapatkan ketika menggunakan 100 neuron tersembunyi dan parameter regularisasi & lambda = 5.0. Saya tidak akan memberikan analisis terperinci tentang pelatihan ulang, ini hanya untuk bersenang-senang, untuk melihat seberapa banyak akurasi dapat dicapai dengan trik baru kami: fungsi biaya dengan entropi silang dan regularisasi L2.

 >>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

Hasil akhirnya adalah akurasi klasifikasi 97,92% pada data pendukung. Sebuah lompatan besar dibandingkan dengan 30 neuron tersembunyi. Anda dapat menyempurnakan sedikit lebih banyak, memulai proses selama 60 zaman dengan η = 0,1 dan λ = 5.0, dan mengatasi penghalang 98%, mencapai akurasi 98,04 pada data pendukung. Tidak buruk untuk 152 baris kode!

Saya menggambarkan regularisasi sebagai cara untuk mengurangi pelatihan ulang dan meningkatkan akurasi klasifikasi. Tapi ini bukan satu-satunya keuntungan. Secara empiris, setelah mencoba melalui banyak peluncuran MNIST jaringan kami, mengubah bobot setiap kali, saya menemukan bahwa peluncuran tanpa regularisasi kadang-kadang “macet”, jelas, jatuh ke minimum lokal dari fungsi biaya. Akibatnya, peluncuran yang berbeda terkadang menghasilkan hasil yang sangat berbeda. Dan regularisasi, sebaliknya, memungkinkan Anda untuk mendapatkan hasil yang lebih mudah direproduksi.

Kenapa begitu? Secara heuristik, ketika fungsi biaya tidak memiliki regularisasi, panjang vektor bobot kemungkinan besar akan tumbuh, semua hal lain dianggap sama. Seiring waktu, ini dapat menyebabkan vektor bobot yang sangat besar. Dan karena ini, vektor skala dapat macet, menunjukkan dalam arah yang kira-kira sama, karena perubahan karena gradient descent hanya membuat perubahan kecil pada arah dengan panjang vektor yang besar. Saya percaya bahwa karena fenomena ini, sangat sulit bagi algoritma pelatihan kami untuk mempelajari ruang bobot dengan benar, dan oleh karena itu sulit untuk menemukan minimum yang baik dari fungsi biaya.