Kebisingan dalam data besar. Analisis Entropi

Saya menemukan tugas yang disebut Enscombe Quartet ( Anscombe ) ”( versi bahasa Inggris ).

Gambar 1 menunjukkan distribusi tabular dari 4 fungsi acak (diambil dari Wikipedia).


Fig. 1. Distribusi tabel dari empat fungsi acak

Gambar 2 menunjukkan parameter distribusi fungsi acak ini


Fig. 2. Parameter distribusi empat fungsi acak

Dan grafiknya pada Gambar 3.


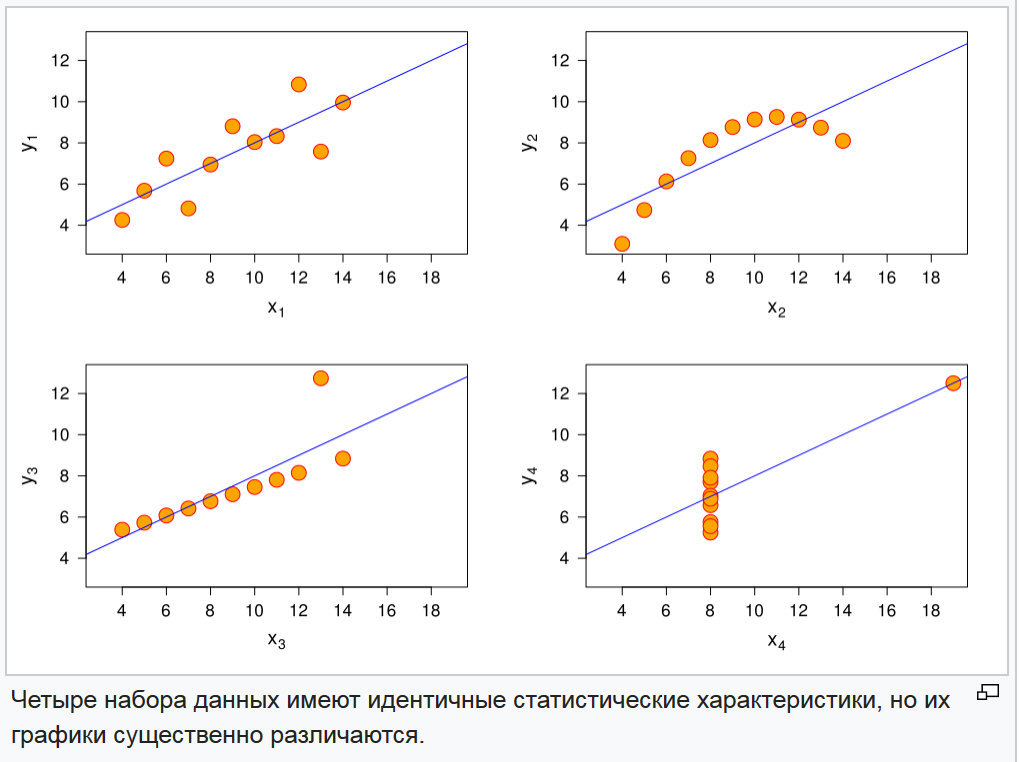Fig. 3. Grafik empat fungsi acak

Masalah membedakan fungsi-fungsi ini diselesaikan cukup sederhana dengan membandingkan momen-momen dari pesanan yang lebih tinggi dan indikator-indikator yang dinormalisasi: koefisien asimetri dan koefisien kelebihan . Indikator-indikator ini disajikan pada Gambar 4.


Fig. 4. Indikator momen dari urutan ketiga dan keempat dan asimetri dan koefisien berlebih dari empat fungsi acak

Seperti dapat dilihat dari tabel pada Gambar 4, kombinasi indikator-indikator ini untuk semua fungsi berbeda.
Kesimpulan pertama, yang secara alami menunjukkan bahwa informasi tentang posisi relatif titik disimpan dalam parameter distribusi pada tingkat yang lebih tinggi daripada varian dari distribusi acak.

Banyak analis mencoba untuk mengisolasi persamaan regresi tertentu dalam data besar dan sejauh ini, hari ini, ini adalah metode pemilihan persamaan dengan dispersi residual terkecil. Tidak banyak yang bisa ditambahkan. Tetapi saya memperhatikan fakta bahwa ini semua informasi, dan informasi memiliki indikator entropi . Dan itu, entropi, memiliki batas dari 0, ketika informasi sepenuhnya ditentukan untuk white noise. Dan white noise di saluran transmisi memiliki distribusi yang seragam.

Ketika diperlukan untuk menganalisis data, pada awalnya diasumsikan bahwa mereka berisi data terkait yang perlu diformalkan sebagai suatu hubungan. Dan ini menunjukkan bahwa data tersebut bukan white noise. Artinya, tahap pertama adalah pemilihan persamaan regresi dan penentuan varian residual. Jika regresi dipilih dengan benar, maka varian residual akan mematuhi hukum distribusi normal. Mari kita lihat dan, dalam Gambar 5-7, rumus entropi untuk variabel acak berdistribusi seragam dan berdistribusi normal disajikan.



Fig. 5. Rumus entropi diferensial untuk kuantitas yang didistribusikan secara normal (VV Afanasyev, Teori Probabilitas dalam Pertanyaan dan Tugas . Kementerian Pendidikan dan Ilmu Pengetahuan Federasi Rusia Universitas Pedagogi Negeri Yaroslavl dinamai dengan KD Ushinsky)


Fig. 6. Rumus entropi diferensial untuk kuantitas yang terdistribusi normal (Pugachev VS Teori fungsi acak dan penerapannya untuk masalah kontrol otomatis . Ed. 2, direvisi dan ditambah. - M.: Fizmatlit, 1960. - 883 p.)


Fig. 7. Rumus entropi diferensial untuk kuantitas yang terdistribusi secara merata (Pugachev VS Teori fungsi acak dan penerapannya pada masalah kontrol otomatis . Ed. 2, direvisi, dan ditambah. - M.: Fizmatlit, 1960. - 883 p.)

Selanjutnya, kami tunjukkan contoh. Tetapi pertama-tama kita mengambil syarat bahwa masing-masing dari empat fungsi adalah koordinat dari hyperplane, yaitu, pada saat yang sama kita memeriksa operasi model dalam ruang multidimensi. Gambar konvolusi hypercube ke pesawat. Mekanisme ini disajikan pada Gambar 8.




Fig. 8. Data awal dengan mekanisme konvolusi


Fig. 9. Pengelompokan agregat dalam gambar.


Fig. 10. Parameter distribusi dari empat fungsi acak dan pengelompokan ringkasan.

Pertimbangkan mekanisme untuk memilih ukuran interval partisi. Kondisi awal disajikan pada Gambar 11.


Fig. 11. Kondisi awal untuk membagi menjadi beberapa interval.

Kondisi 1. Harus dengan probabilitas nol di wilayah variasi, karena jika tidak, entropi sama dengan tak terhingga. Baik untuk sampel awal maupun residual.

Kondisi 2. Karena tidak mungkin untuk mengabaikan kemungkinan pencilan dalam data baru, dll., Untuk interval ekstrim, maka perlu untuk menetapkan probabilitas sesuai dengan hukum teoritis distribusi probabilitas normal atau yang lain yang berlaku umum, sesuai dengan prinsip probabilitas ekor.

Kondisi 3. Langkah interval harus menyediakan jumlah interval minimum yang diperlukan pada penyebaran sampel residu.

Kondisi 4. Jumlah interval harus ganjil.

Kondisi 5. Jumlah interval harus memastikan persetujuan yang dapat diandalkan dengan hukum distribusi teoritis yang dipilih untuk penelitian.


Fig. 12. Sisa dari distribusi

Tentukan mekanisme pemilihan interval pada Gambar 13.


Fig. 13. Algoritma pemilihan interval

Masalah utama, menurut saya, adalah memutuskan untuk memperkenalkan interval ekor atau tidak. Jika untuk dispersi residu terlihat cukup alami, maka untuk seri utama, itu cukup tegang.


Fig. 14. Hasil pengolahan nilai-nilai data dalam menentukan entropi informasi

Kesimpulan Di mana alat ini bisa diterapkan

Membandingkan indikator yang dihasilkan dari tabel pada Gambar 14, dapat dilihat bahwa mereka menanggapi perubahan dalam struktur data. Dan ini berarti alat tersebut memiliki sensitivitas, dan memungkinkan Anda untuk menyelesaikan masalah yang mirip dengan tugas kuartet Enskomb.

Tanpa ragu, masalah ini dapat diselesaikan dengan bantuan momen pesanan yang lebih tinggi. Tetapi pada intinya, entropi informasi tergantung pada varians dari variabel acak, yaitu, itu adalah karakteristik varian pihak ketiga. Jadi, kita dapat menunjukkan interval di mana penggunaan analisis varian dapat mengarah pada hasil tertentu.

Karakteristik numerik dari entropi memungkinkan untuk melakukan analisis korelasi dengan variabel independen. Sebagai salah satu contoh manifestasi dari koneksi yang mungkin, berikut ini: Misalkan, selama interval dari a ke b, tingkat kebisingan dari serangkaian data meningkat, membandingkan nilai variabel independen, kami menemukan bahwa variabel xn memasuki kisaran lebih dari 5 unit, setelah itu variabel, menurun di bawah +5, kebisingan berkurang. Selanjutnya, pemeriksaan tambahan dapat dilakukan dan, jika hipotesis ini dikonfirmasi, maka dalam penelitian lebih lanjut, melarang variabel xn naik di atas +5. Karena dalam kasus ini, data menjadi tidak berguna.

Saya berasumsi bahwa ada opsi lain untuk menggunakan alat ini.

Bagaimana cara menggunakan

Dalam aspek ini, mekanisme alami "moving average" diperiksa, saya kira ukuran sampel yang diperoleh dengan rumus ukuran sampel dari analisis statistik akan memberikan volume yang wajar dari area slip. Menurut analisis saat ini, disimpulkan bahwa ukuran sampel harus ditentukan dari proporsi minimum yang jatuh pada probabilitas terkecil. Dalam contoh kami, untuk varian residual, fraksi minimum interval empiris adalah 0,15909. Ini harus dilakukan, karena jika interval apa pun dalam volume slip ternyata kosong, maka dalam hal ini angka kebisingan akan menjadi keterlaluan atau aturan akan bekerja bahwa logaritma 0 sama dengan minus infinity. Dan dengan ukuran sampel yang dipilih dengan benar, nilai-nilai transendental dari indikator ini akan menunjukkan perubahan besar dalam struktur informasi.