Pengambilan sampel dan akurasi perhitungan

Sejumlah kolega saya dihadapkan dengan masalah bahwa untuk menghitung beberapa jenis metrik, misalnya, tingkat konversi, Anda harus memvalidasi seluruh basis data. Atau Anda perlu melakukan studi terperinci untuk setiap klien, di mana ada jutaan pelanggan. Kerry jenis ini dapat bekerja cukup lama, bahkan dalam repositori yang dibuat khusus. Tidak terlalu menyenangkan untuk menunggu 5-15-40 menit sampai metrik sederhana dianggap mengetahui bahwa Anda perlu menghitung sesuatu yang lain atau menambahkan sesuatu yang lain.

Salah satu solusi untuk masalah ini adalah pengambilan sampel: kami tidak mencoba menghitung metrik kami pada seluruh array data, tetapi mengambil subset yang secara representatif mewakili metrik yang kami butuhkan. Sampel ini bisa 1000 kali lebih kecil dari susunan data kami, tetapi cukup baik untuk menunjukkan angka yang kami butuhkan.

Dalam artikel ini, saya memutuskan untuk menunjukkan bagaimana ukuran sampel sampel memengaruhi kesalahan metrik akhir.

Masalah

Pertanyaan kuncinya adalah: seberapa baik sampel menggambarkan “populasi”? Karena kami mengambil sampel dari array umum, metrik yang kami terima ternyata menjadi variabel acak. Sampel yang berbeda akan memberi kita hasil metrik yang berbeda. Beda, tidak berarti apa-apa. Teori probabilitas memberi tahu kita bahwa nilai metrik yang diperoleh dengan pengambilan sampel harus dikelompokkan di sekitar nilai metrik sebenarnya (dibuat di atas seluruh sampel) dengan tingkat kesalahan tertentu. Selain itu, kita sering mengalami masalah di mana tingkat kesalahan yang berbeda dapat ditiadakan. Adalah satu hal untuk mengetahui apakah kami mendapatkan konversi 50% atau 10%, dan itu hal lain untuk mendapatkan hasil dengan akurasi 50,01% vs 50,02%.

Sangat menarik bahwa dari sudut pandang teori, koefisien konversi yang diamati oleh kami atas seluruh sampel juga merupakan variabel acak, karena Tingkat konversi "teoritis" hanya dapat dihitung pada sampel dengan ukuran tak terbatas. Ini berarti bahwa bahkan semua pengamatan kami dalam basis data benar-benar memberikan perkiraan konversi dengan keakuratannya, meskipun bagi kami angka-angka yang dihitung ini benar-benar akurat. Ini juga mengarah pada kesimpulan bahwa bahkan jika hari ini tingkat konversi berbeda dari kemarin, ini tidak berarti bahwa sesuatu telah berubah, tetapi hanya berarti bahwa sampel saat ini (semua pengamatan dalam database) berasal dari populasi umum (semua mungkin pengamatan untuk hari ini, yang terjadi dan tidak terjadi) memberikan hasil yang sedikit berbeda dari kemarin. Bagaimanapun, untuk setiap produk atau analis yang jujur, ini harus menjadi hipotesis dasar.

Pernyataan tugas

Katakanlah kita memiliki 1.000.000 catatan dalam database tipe 0/1, yang memberi tahu kami apakah konversi telah terjadi pada suatu acara. Maka tingkat konversi hanyalah jumlah 1 dibagi 1 juta.

Pertanyaan: jika kita mengambil sampel berukuran N, berapa banyak dan dengan probabilitas apa perbedaan tingkat konversi dari yang dihitung atas seluruh sampel?

Pertimbangan teoretis

Tugas dikurangi untuk menghitung interval kepercayaan dari koefisien konversi untuk sampel dengan ukuran tertentu untuk distribusi binomial.

Dari teori, simpangan baku untuk distribusi binomial adalah:
S = sqrt (p * (1 - p) / N)

Dimana
p - tingkat konversi
N - Ukuran Sampel
S - standar deviasi

Saya tidak akan mempertimbangkan interval kepercayaan langsung dari teori. Ada matan yang agak rumit dan membingungkan, yang akhirnya menghubungkan standar deviasi dan estimasi akhir dari interval kepercayaan.

Mari kita kembangkan "intuisi" tentang rumus standar deviasi:

1. Semakin besar ukuran sampel, semakin kecil kesalahannya. Dalam kasus ini, kesalahan jatuh dalam ketergantungan kuadrat terbalik, mis. menambah sampel sebanyak 4 kali meningkatkan akurasi hanya 2 kali. Ini berarti bahwa pada titik tertentu meningkatkan ukuran sampel tidak akan memberikan keuntungan tertentu, dan juga berarti bahwa akurasi yang cukup tinggi dapat diperoleh dengan sampel yang cukup kecil.

1. Ada ketergantungan kesalahan pada nilai tingkat konversi. Kesalahan relatif (yaitu, rasio kesalahan dengan nilai tingkat konversi) memiliki kecenderungan "keji" untuk menjadi lebih besar, semakin rendah tingkat konversi:

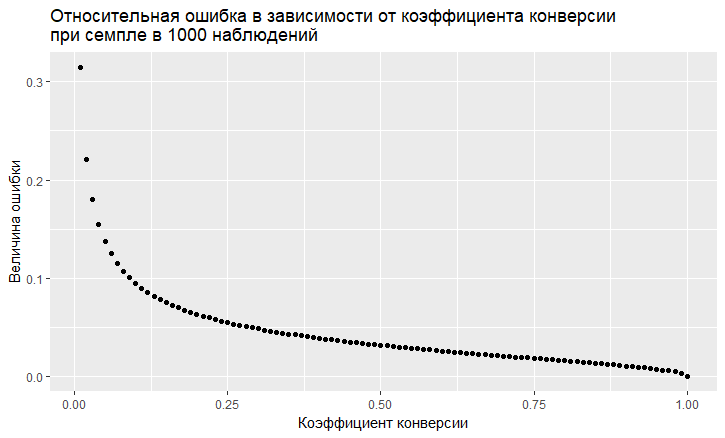
1. Seperti yang kita lihat, kesalahan "terbang" ke langit dengan tingkat konversi yang rendah. Ini berarti bahwa jika Anda mencicipi peristiwa langka, maka Anda memerlukan ukuran sampel yang besar, jika tidak, Anda akan mendapatkan taksiran konversi dengan kesalahan yang sangat besar.

Pemodelan

Kita dapat sepenuhnya menjauh dari solusi teoretis dan menyelesaikan masalah "langsung". Berkat bahasa R, ini sekarang sangat mudah dilakukan. Untuk menjawab pertanyaan, kesalahan apa yang kita dapatkan saat pengambilan sampel, Anda bisa melakukan seribu sampel dan melihat kesalahan apa yang kita dapatkan.

Pendekatannya adalah ini:

1. Kami mengambil tingkat konversi yang berbeda (dari 0,01% menjadi 50%).
2. Kami mengambil 1000 sampel dari 10, 100, 1000, 10.000, 50.000, 100.000, 250.000, 500.000 elemen dalam sampel
3. Kami menghitung tingkat konversi untuk setiap kelompok sampel (1000 koefisien)
4. Kami menyusun histogram untuk setiap kelompok sampel dan menentukan sejauh mana tingkat konversi 60%, 80%, dan 90% yang diamati berada.

Data penghasil kode R:

sample.size <- c(10, 100, 1000, 10000, 50000, 100000, 250000, 500000) bootstrap = 1000 Error <- NULL len = 1000000 for (prob in c(0.0001, 0.001, 0.01, 0.1, 0.5)){ CRsub <- data.table(sample_size = 0, CR = 0) v1 = seq(1,len) v2 = rbinom(len, 1, prob) set = data.table(index = v1, conv = v2) print(paste('probability is: ', prob)) for (j in 1:length(sample.size)){ for(i in 1:bootstrap){ ss <- sample.size[j] subset <- set[round(runif(ss, min = 1, max = len),0),] CRsample <- sum(subset$conv)/dim(subset)[1] CRsub <- rbind(CRsub, data.table(sample_size = ss, CR = CRsample)) } print(paste('sample size is:', sample.size[j])) q <- quantile(CRsub[sample_size == ss, CR], probs = c(0.05,0.1, 0.2, 0.8, 0.9, 0.95)) Error <- rbind(Error, cbind(prob,ss,t(q))) } 

Hasilnya, kita mendapatkan tabel berikut (akan ada grafik nanti, tetapi detailnya lebih baik terlihat dalam tabel).

Mari kita lihat kasus dengan konversi 10% dan dengan konversi 0,01% rendah, karena semua fitur bekerja dengan sampling terlihat jelas pada mereka.

Pada konversi 10%, gambar terlihat sangat sederhana:

Poin adalah tepi dari interval kepercayaan 5-95%, mis. membuat sampel, kami akan dalam 90% kasus mendapatkan CR pada sampel dalam interval ini. Skala vertikal - ukuran sampel (skala logaritmik), horizontal - nilai tingkat konversi. Bilah vertikal adalah CR "benar".

Kami melihat hal yang sama yang kami lihat dari model teoretis: akurasi meningkat ketika ukuran sampel bertambah, dan satu konvergen cukup cepat dan sampel mendapatkan hasil mendekati "benar". Total untuk 1000 sampel kami memiliki 8,6% - 11,7%, yang akan cukup untuk sejumlah tugas. Dan dalam 10 ribu sudah 9,5% - 10,55%.

Hal-hal buruk dengan kejadian langka dan ini konsisten dengan teori:

Pada tingkat konversi yang rendah 0,01%, masalahnya adalah statistik pada 1 juta pengamatan, dan dengan sampel situasinya bahkan lebih buruk. Kesalahannya hanya raksasa. Pada sampel hingga 10.000, metrik pada prinsipnya tidak valid. Misalnya, pada sampel 10 pengamatan, generator saya baru saja 0 konversi 1000 kali, jadi hanya ada 1 poin. Pada 100 ribu, kita memiliki sebaran dari 0,005% hingga 0,0016%, yaitu kita dapat membuat hampir setengah koefisien dengan pengambilan sampel seperti itu.

Perlu juga dicatat bahwa ketika Anda mengamati konversi dalam skala kecil hingga 1 juta uji coba, maka Anda hanya memiliki kesalahan alami yang besar. Dari sini dapat disimpulkan bahwa dinamika kejadian langka seperti itu harus dilakukan pada sampel yang sangat besar, jika tidak, Anda hanya mengejar hantu, fluktuasi acak dalam data.

Kesimpulan:

1. Mengambil sampel metode kerja untuk mendapatkan taksiran
2. Akurasi sampel meningkat dengan meningkatnya ukuran sampel dan berkurang dengan penurunan tingkat konversi.
3. Keakuratan estimasi dapat dimodelkan untuk tugas Anda dan dengan demikian pilih sampel yang optimal untuk Anda sendiri.
4. Penting untuk diingat bahwa peristiwa langka tidak dapat dicicipi dengan baik
5. Secara umum, kejadian langka sulit untuk dianalisis, mereka memerlukan sampel data besar tanpa sampel.