Algoritma kriptografi Grasshopper: kompleks

Artikel ini akan merinci algoritma enkripsi blok yang didefinisikan dalam GOST R 34.12-2015 sebagai Belalang. Apa itu berdasarkan, apa matematika dari algoritma blok kriptografi, dan bagaimana algoritma ini diimplementasikan di java.

Siapa, bagaimana, kapan, dan mengapa dikembangkan algoritme ini akan tetap berada di luar cakupan artikel, karena dalam hal ini kami tidak begitu tertarik, kecuali:

Belalang = Kuznetsov, Nechaev DAN Perusahaan.



Karena kriptografi terutama didasarkan pada matematika, sehingga penjelasan lebih lanjut tidak menimbulkan banyak pertanyaan, Anda harus terlebih dahulu menganalisis konsep dasar dan fungsi matematika di mana algoritma ini dibangun.

Fields Galois

Aritmatika bidang Galois adalah aritmatika polinomial, yaitu, setiap elemen bidang ini adalah polinomial. Hasil dari operasi apa pun juga merupakan elemen dari bidang ini. Bidang Galois tertentu terdiri dari rentang angka yang tetap. Karakteristik lapangan disebut beberapa bilangan prima p. Pesanan lapangan, mis. jumlah unsur-unsurnya adalah tingkat karakteristik alami tertentu $$$p ^ m$ , di mana m ϵ N. Untuk m = 1, bidang ini disebut sederhana. Dalam kasus di mana m> 1, untuk pembentukan bidang, polinomial pembangkit derajat m juga diperlukan, bidang semacam itu disebut diperluas. $$$Gf (p ^ m)$ - Penunjukan bidang Galois. Polinomial pembangkit tidak dapat direduksi, yaitu sederhana (dengan analogi dengan bilangan prima ia dapat dibagi oleh 1 dan dengan sendirinya tanpa sisa). Karena bekerja dengan informasi apa pun bekerja dengan byte, dan byte adalah 8 bit, ambil sebagai bidang $$$Gf (2 ^ 8)$ dan polinomial penghasil:

$$

$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1.$$

Namun, untuk memulainya, kami akan menganalisis operasi dasar di bidang yang lebih sederhana $$$Gf (2 ^ 3)$ dengan menghasilkan polinomial $$$f (x) = x ^ 3 + x + 1$ .

Operasi penambahan

Yang paling sederhana adalah operasi penjumlahan, yang dalam bidang aritmatika Galois adalah modulo 2 penambahan bitwise sederhana (R).

Saya segera menarik perhatian pada fakta bahwa tanda "+" di sini dan selanjutnya mengacu pada operasi bitwise XOR, dan bukan penambahan dalam bentuk yang biasa.

Tabel kebenaran fungsi HOR



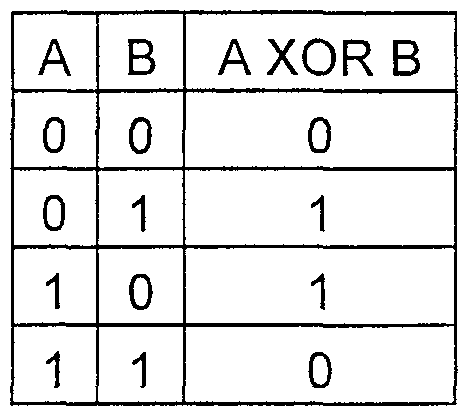
Contoh: $$$5 + 3 = 101 + 011 = 110_2 = 6_ {10}$

Dalam bentuk polinomial, operasi ini akan terlihat seperti

$$

$$(x ^ 2 + 1) + (x + 1) = x ^ 2 + x = 110_2 = 6_ {10}$$

Operasi multiplikasi

Untuk melakukan operasi penggandaan, perlu untuk mengubah angka menjadi bentuk polinom:

$$

$$5 = 101_2 = 1 * x ^ 2 + 0 * x ^ 1 + 1 * x ^ 0 = x ^ 2 + 1$$

Seperti yang Anda lihat, angka dalam bentuk polinom adalah polinomial yang koefisiennya adalah nilai-nilai digit dalam representasi biner dari angka tersebut.

Gandakan dua angka dalam bentuk polinomial:

$$

$$5 * 7 = (x ^ 2 + 1) * (x ^ 2 + x + 1) = x ^ 4 + x ^ 3 + x ^ 2 + x ^ 2 + x + 1 =$$

$$

$$= x ^ 4 + x ^ 3 + x + 1 = 11011_2 = 27_ {10}$$

Hasil perkalian 27 tidak di bidang yang digunakan. $$$Gf (2 ^ 3)$ (Terdiri dari angka dari 0 hingga 7, seperti yang disebutkan di atas). Untuk mengatasi masalah ini, perlu menggunakan polinomial pembangkit.

Juga diasumsikan bahwa x memenuhi persamaan $$$f (x) = x ^ 3 + x + 1 = 0$ lalu



Mari kita buat tabel perkalian:



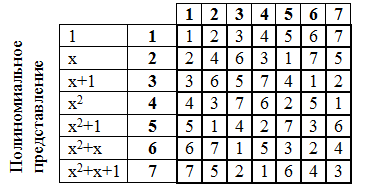
Yang sangat penting adalah tabel derajat unsur-unsur bidang Galois. Meningkatkan kekuatan juga dilakukan dalam bentuk polinomial, mirip dengan perkalian.

Contoh:

$$

$$5 ^ 2 = (x ^ 2 + 1) ^ 2 = x ^ 4 + x ^ 2 + x ^ 2 + 1 = x ^ 4 + x ^ 2 + x + x ^ 2 + x + 1 =$$

$$

$$= x (x ^ 3 + x + 1) + x ^ 2 + x + 1 = x ^ 2 + x + 1 = 111_2 = 7_ {10}$$

Jadi, kami menyusun tabel derajat:



Tabel derajat bersifat siklis: tingkat ketujuh sama dengan nol, sehingga tingkat kedelapan berhubungan dengan yang pertama, dll. Anda dapat memeriksa ini jika mau.

Dalam bidang Galois, ada konsep istilah primitif - elemen bidang yang derajatnya mengandung semua elemen bukan-nol dari bidang tersebut. Dapat dilihat bahwa semua elemen sesuai dengan kondisi ini (tentu saja, kecuali 1). Namun, ini tidak selalu terjadi.

Untuk bidang yang kami pertimbangkan, yaitu, dengan karakteristik 2, selalu memilih 2. Sebagai anggota primitif, mengingat propertinya, elemen apa pun dari bidang tersebut dapat dinyatakan dalam derajat derajat anggota primitif.



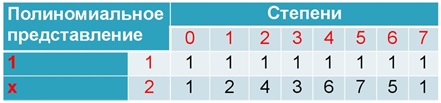
Contoh: $$$5 = 2 ^ 6,7 = 2 ^ 5$

Dengan menggunakan properti ini, dan dengan mempertimbangkan siklus tabel derajat, kami akan mencoba mengalikan angka lagi:

$$

$$5 * 7 = 2 ^ 6 * 2 ^ 5 = 2 ^ {(6 + 5)} = 2 ^ {(11mod7)} = 2 ^ 4 = 6$$

Hasilnya bertepatan dengan apa yang kami hitung sebelumnya.

Sekarang mari kita lakukan pembagian:

$$

$$6/5 = 2 ^ 4/2 ^ 6 = 2 ^ {(4-6)} = 2 ^ {((- 2) mod7)} = 2 ^ 5 = 7$$

Hasil yang didapat juga benar.

Nah, demi kelengkapan, mari kita lihat mengangkat ke kekuatan:

$$

$$5 ^ 2 = (2 ^ 6) ^ 2 = 2 ^ {(6 * 2)} = 2 ^ {(12mod7)} = 2 ^ 5 = 7$$

Pendekatan semacam itu untuk perkalian dan pembagian jauh lebih sederhana daripada operasi nyata menggunakan polinomial, dan bagi mereka tidak perlu menyimpan tabel perkalian besar, tetapi hanya deretan derajat anggota bidang primitif.

Sekarang kembali ke bidang kita $$$Gf (2 ^ 8)$

Elemen nol bidang adalah satu, elemen 1 adalah elemen dua, setiap elemen berikutnya dari elemen ke-2 dan ke-254 dihitung sebagai elemen sebelumnya, dikalikan dengan 2, dan jika elemen tersebut di luar bidang, yaitu, nilainya lebih besar dari $$$(2 ^ 8-1)$ maka XOR dilakukan dengan nomor tersebut $$$195_ {10}$ , angka ini mewakili polinomial tak tereduksi dari bidang tersebut $$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1 = 2 ^ 8 + 2 ^ 7 ++ 2 ^ 6 + 2 + 1 = 451$ , kami membawa nomor ini ke lapangan $$$451-256 = $ 19$ . Dan elemen 255 adalah lagi 1. Jadi kami memiliki bidang yang berisi 256 elemen, yaitu, set byte lengkap, dan kami telah menganalisis operasi dasar yang dilakukan di bidang ini.



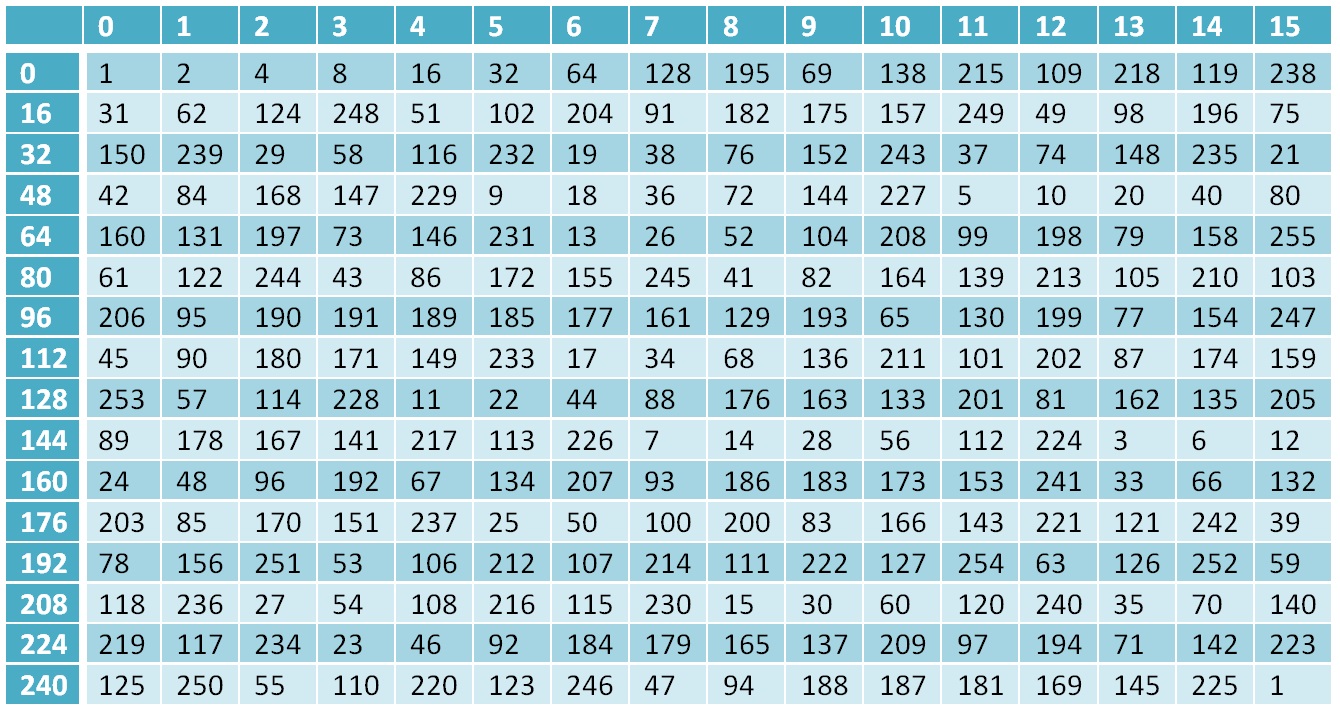
Tabel kekuatan dua untuk lapangan $$$Gf (2 ^ 8)$

Mengapa itu diperlukan - bagian dari perhitungan di algoritma Grasshopper dilakukan di bidang Galois, dan hasil perhitungan, masing-masing, adalah elemen dari bidang ini.

Jaringan Feistel

Feistel Network adalah metode enkripsi blok yang dikembangkan oleh Horst Feistel di IBM pada tahun 1971. Jaringan Feistel saat ini adalah dasar dari sejumlah besar protokol kriptografi.

Jaringan Feistel beroperasi dengan blok teks-jelas:

1. Blok ini dibagi menjadi dua bagian yang sama - L kiri dan kanan R.
2. Sub-blok kiri L diubah oleh fungsi f menggunakan tombol K: X = f (L, K). Sebagai fungsi, bisa ada transformasi apa pun.
3. Sub-blok X yang dihasilkan ditambahkan modulo 2 dengan sub-blok kanan R, yang tetap tidak berubah: X = X + R.
4. Bagian yang dihasilkan dipertukarkan dan dilem.

Urutan tindakan ini disebut sel Feistel.


Gambar 1. Sel Feistel

Jaringan Feistel terdiri dari beberapa sel. Subblok yang diperoleh pada output sel pertama menuju input sel kedua, subblok yang dihasilkan dari sel kedua menuju input sel ketiga dan seterusnya.

Algoritma enkripsi

Sekarang kita telah menjadi akrab dengan operasi yang digunakan dan dapat beralih ke topik utama - yaitu, cryptolgoritma Grasshopper.

Dasar dari algoritma ini adalah yang disebut jaringan SP - jaringan Substitusi-Permutasi. Cipher yang didasarkan pada jaringan SP menerima blok dan kunci pada input dan melakukan beberapa putaran bolak-balik yang terdiri dari tahap substitusi dan tahap permutasi. Grasshopper melakukan sembilan putaran penuh, yang masing-masing mencakup tiga operasi berturut-turut:

1. Operasi penerapan kunci bulat atau bitor XOR dari kunci dan blok data input;
2. Konversi non-linear, yang merupakan penggantian sederhana satu byte dengan byte lain sesuai dengan tabel;
3. Transformasi linier. Setiap byte dari blok dikalikan dalam bidang Galois oleh salah satu koefisien dari seri (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1) tergantung pada ordinal nomor byte (seri disajikan untuk nomor seri dari tanggal 15 hingga tanggal 0, seperti yang ditunjukkan pada gambar). Bytes ditambahkan bersama-sama modulo 2, dan semua 16 byte blok digeser ke arah urutan rendah, dan jumlah yang dihasilkan dituliskan sebagai pengganti byte baca.

Babak kesepuluh terakhir tidak lengkap, hanya mencakup operasi XOR pertama.

Grasshopper adalah algoritma blok, ia bekerja dengan blok data dengan panjang 128 bit atau 16 byte. Panjang kuncinya adalah 256 bit (32 byte).


Gambar 2. Skema enkripsi dan dekripsi dari blok data

Diagram menunjukkan urutan operasi, di mana S adalah transformasi non-linear, L adalah transformasi linier, Ki adalah kunci bulat. Pertanyaan segera muncul - dari mana kunci bulat itu berasal.

Formasi Kunci Bulat

Kunci iteratif (atau bundar) diperoleh dengan transformasi tertentu berdasarkan kunci master, yang panjangnya, seperti yang sudah kita ketahui, adalah 256 bit. Proses ini dimulai dengan memisahkan kunci utama menjadi dua, sehingga pasangan pertama dari kunci bulat diperoleh. Delapan iterasi jaringan Feistel digunakan untuk menghasilkan setiap pasangan kunci putaran berikutnya, sebuah konstanta digunakan pada setiap iterasi, yang dihitung dengan menerapkan transformasi linear dari algoritma ke nilai nomor iterasi.


Skema untuk mendapatkan kunci berulang (bulat)

Jika kita mengingat Gambar 1, maka sub-blok kiri L adalah setengah kiri dari kunci asli, sub-blok kanan R adalah separuh kanan dari kunci asli, K adalah konstanta Ci, fungsi f adalah urutan operasi R XOR Ci, transformasi non-linear, transformasi linear.

Konstanta iterasi Ci diperoleh dengan menggunakan L-transformasi dari nomor urut iterasi.

Jadi, untuk mengenkripsi blok teks, pertama-tama kita harus menghitung 32 konstanta iteratif, kemudian menghitung 10 kunci putaran berdasarkan kunci, dan kemudian melakukan urutan operasi yang ditunjukkan pada Gambar 2.

Mari kita mulai dengan menghitung konstanta:
Const pertama $$$C_1 = 1_ {10} = 00000001_2 = 01_ {16}$ Namun, semua transformasi dalam algoritma kami dilakukan dengan blok sepanjang 16 byte, oleh karena itu perlu menambah konstanta dengan panjang blok, yaitu, menambahkan 15 nol byte ke kanan, kita dapatkan

$$

$$C_1 = 01000000000000000000000000000000 $$$

Lipat gandakan dengan seri (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) sebagai berikut:

$$

$$a_ {15} = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 +$$

$$

$$+ a_5 * 194 + a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

(Kesetaraan ini diberikan dalam operasi bidang Galois)
Karena semuanya kecuali byte nol sama dengan 0, dan byte nol dikalikan dengan 1, kita mendapatkan 1 dan menuliskannya ke urutan tinggi dari angka, menggeser semua byte ke urutan rendah, kita mendapatkan:

$$

$$C_1 = 00000000000000000000000000000001$$

Ulangi operasi yang sama. Kali ini $$$a_ {15} = 1$ , semua byte lainnya adalah 0, oleh karena itu, hanya sisa pertama dari ketentuan $$$a_ {15} * 148 = 1 * 148 = 148_ {10} = 94_ {16}$ kami mendapatkan:

$$

$$C_1 = 00000000000000000000000000000194$$

Kami melakukan iterasi ketiga, berikut adalah dua istilah yang bukan nol:

$$

$$a_ {15} * 148 + a_ {14} * 32 = 148 * 148 + 1 * 32 =$$

$$

$$= 10010100 * 10010100 + 00000001 * 00100000 =$$

$$

$$= (x ^ 7 + x ^ 4 + x ^ 2) * (x ^ 7 + x ^ 4 + x ^ 2) + 1 * x ^ 5 = x ^ {14} + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 6 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {13} + x ^ {12} + x ^ 7 + x ^ 6 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 5 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {11} + x ^ 5 + x ^ 7 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 3 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {10} + x ^ 9 + x ^ 3 + x ^ 8 + x ^ 7 =$$

$$

$$= x ^ 2 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ 2 + x ^ 7 = x ^ 7 + x ^ 2 = 132_ {10}$$

$$

$$132_ {10} = 84_ {16}$$

Menurut tabel derajat, itu bisa diselesaikan lebih mudah:

$$

$$148 * 148 + 1 * 32 = 2 ^ {45} * 2 ^ {45} + 2 ^ 5 = 2 ^ {90} + 2 ^ 5 = 164 + 32 = 132$$

$$

$$C_1 = 00000000000000000000000000019484$$

Selanjutnya, semuanya persis sama, hanya 16 iterasi untuk setiap konstanta

$$

$$C_1 = 000000000000000000000000019484DD$$

$$

$$C_1 = 0000000000000000000000019484DD10$$

$$

$$C_1 = 00000000000000000000019484DD10BD$$

$$

$$C_1 = 000000000000000000019484DD10BD27$$

$$

$$C_1 = 0000000000000000019484DD10BD275D$$

$$

$$C_1 = 00000000000000019484DD10BD275DB8$$

$$

$$C_1 = 000000000000019484DD10BD275DB87A$$

$$

$$C_1 = 0000000000019484DD10BD275DB87A48$$

$$

$$C_1 = 00000000019484DD10BD275DB87A486C$$

$$

$$C_1 = 000000019484DD10BD275DB87A486C72$$

$$

$$C_1 = 0000019484DD10BD275DB87A486C727$$

$$

$$C_1 = 00019484DD10BD275DB87A486C7276A2$$

Dan konstanta terakhir:

$$

$$C_1 = 019484DD10BD275DB87A486C7276A2E6$$

Konstanta lain:

$$

$$C_2 = 02EBCB7920B94EBAB3F490D8E4EC87DC$$

$$

$$C_3 = 037F4FA4300469E70B8ED8B4969A25B2$$

$$

$$C_4 = 041555F240B19CB7A52BE3730B1BCD7B$$

$$

$$C_5 = 0581D12F500CBBEA1D51AB1F796D6F15$$

$$

$$C_6 = 06FE9E8B6008D20D16DF73ABEFF74AA7$$

$$

$$C_7 = 076A1A5670B5F550AEA53BC79D81E8C9$$

$$

$$C_8 = 082AAA2780A1FBAD895605E6163659F6$$

$$

$$C_9 = 09BE2EFA901CDCF0312C4D8A6440FB98$$

$$

$$C_ {10} = 0AC1615EA018B5173AA2953EF2DADE2A$$

$$

$$C_ {11} = 0B5PUBL83B0A5924A82D8DD5280AC7C44$$

$$

$$C_ {12} = 0C3FFFD5C010671A2C7DE6951D2D948D$$

$$

$$C_ {13} = 0DAB7B08D0AD40479407AEF96F5B36E3$$

$$

$$C_ {14} = 0ED434ACE0A929A09F89764DF9C11351$$

$$

$$C_ {15} = 0F40B071F0140EFD27F33E218BB7B13F$$

$$

$$C_ {16} = 1054974EC3813599D1AC0A0F2C6CB22F$$

$$

$$C_ {17} = 11C01393D33C12C469D642635E1A1041$$

$$

$$C_ {18} = 12BF5C37E3387B2362589AD7C88035F3$$

$$

$$C_ {19} = 132BD8EAF3855C7EDA22D2BBBAF6979D$$

$$

$$C_ {20} = 1441C2BC8330A92E7487E97C27777F54$$

$$

$$C_ {21} = 15D54661938D8E73CCFDA1105501DD3A$$

$$

$$C_ {22} = 16AA09C5A389E794C77379A4C39BF888$$

$$

$$C_ {23} = 173E8D18B334C0C97F0931C8B1ED5AE6$$

$$

$$C_ {24} = 187E3D694320CE3458FA0FE93A5AEBD9$$

$$

$$C_ {25} = 19EAB9B4539DE969E0804785482C49B7$$

$$

$$C_ {26} = 1A95F6106399808EEB0E9F31DEB66C05$$

$$

$$C_ {27} = 1B0172CD7324A7D35374D75DACC0CE6B$$

$$

$$C_ {28} = 1C6B689B03915283FDD1EC9A314126A2$$

$$

$$C_ {29} = 1DFFEC46132C75DE45ABA4F6433784CC$$

$$

$$C_ {30} = 1E80A3E223281C394E257C42D5ADA17E$$

$$

$$C_ {31} = 1F14273F33953B64F65F342EA7DB0310$$

$$

$$C_ {32} = 20A8ED9C45C16AF1619B141E58D8A75E$$

Sekarang kita akan menghitung kunci bundar sesuai dengan skema yang disajikan di atas, ambil kunci enkripsi:

$$

$$K = 7766554433221100FFEEDDCCBBAA9988$$

$$

$$EFCDAB89674523011032547698BADCFE$$

Lalu

$$

$$K_1 = 7766554433221100FFEEDDCCBBAA9988$$

$$

$$K_2 = EFCDAB89674523011032547698BADCFE$$

$$$K_1$ akan menjadi sub-blok kiri jaringan Feistel, dan $$$K_2$ - benar.
Ayo lakukan operasi $$$K_1 + C_1$
Byte pertama $$$K_1$ sama dengan $$$77_ {16} = 01110111_2$
Byte pertama $$$C_1$ sama dengan $$$01_ {16} = 00000001_2$

$$

$$01110111_2 + 00000001_2 = 01110110_2 = 76_ {16}$$

byte yang tersisa dikonversi dengan cara yang sama, sebagai hasilnya $$$X (K_1, C_1) = K_1 + C_1$ :

$$

$$X (K_1, C_1) = 76F2D199239F365D479495A0C9DC3BE6$$

Selanjutnya, kami melakukan transformasi nonlinier $$$S (X (K_1, C_1))$ . Ini dilakukan sesuai dengan tabel:


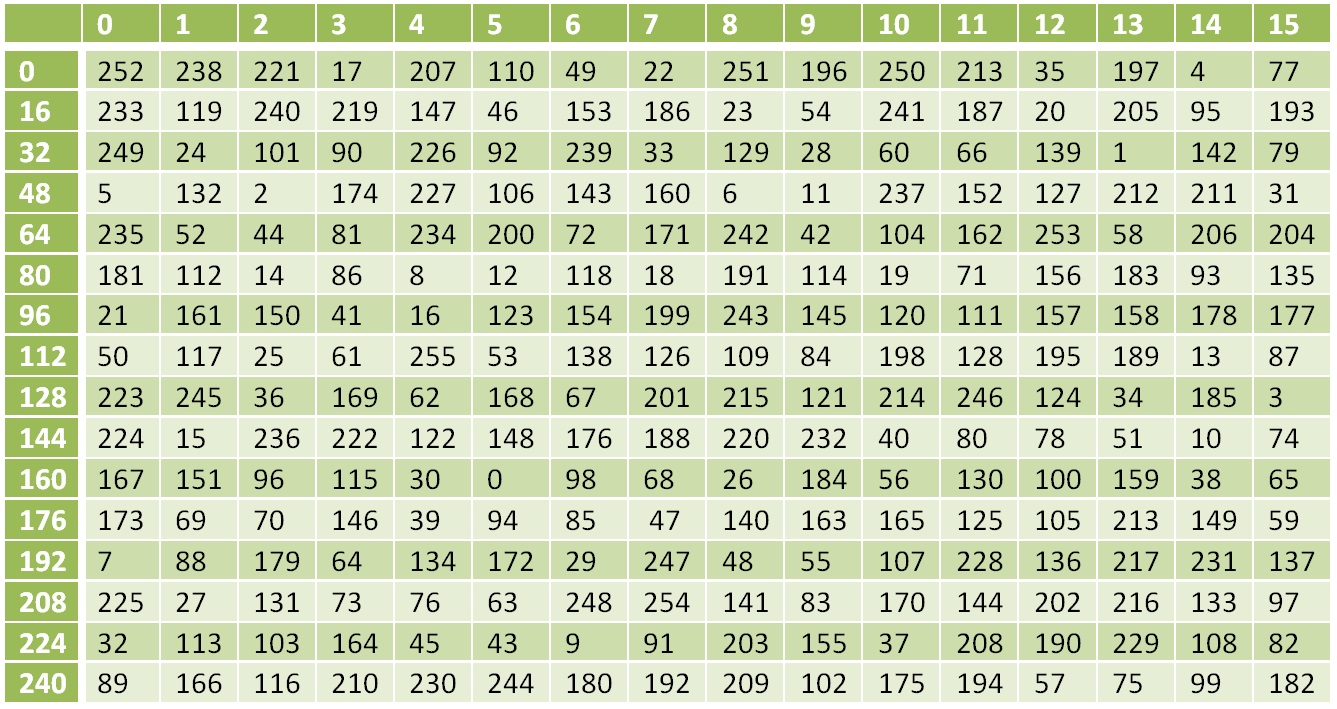Tabel konversi nonlinier

Angka 0 diganti dengan 252, 1 oleh 238, 17 oleh 119, dll.

$$

$$76_ {16} = 118_ {10}$$

$$

$$S (118) = 138_ {10} = 8A_ {16}$$

$$

$$S (X (K_1, C_1)) = 8A741BE85A4A8FB7AB7A94A737CA9809$$

Sekarang lakukan transformasi linear $$$L (S (X (K_1, C_1)))$ , itu dipertimbangkan secara rinci ketika menghitung konstanta iteratif, jadi di sini kami hanya memberikan hasil akhir:

$$

$$L (S (X (K_1, C_1)))) = A644615E1D0757926A5DB79D9940093D$$

Menurut skema sel Feistel, kami melakukan XOR dengan sub-blok kanan, yaitu, dengan $$$K_2$ :

$$

$$X (L (S (X (K_1, C_1))), K_2) = 4989CAD77A4274937A6FE3EB01FAD5C3$$

Dan hasil yang diperoleh pada output sel Feistel pertama:

$$

$$EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3$$

Nilai ini dibagi dua dan masuk ke input sel Feistel kedua, di mana konstanta kedua sudah digunakan $$$C_2$ . Setelah melalui delapan sel, kita mendapatkan 2 kunci berikut $$$K_3$ dan $$$K_4$ . Kami akan melakukan delapan iterasi jaringan Feistel dengan mereka, dapatkan pasangan kunci berikutnya, dan seterusnya. Delapan iterasi per pasangan kunci, karena kita awalnya memiliki pasangan pertama, maka 32 iterasi dilakukan secara total, masing-masing dengan konstanta sendiri.

Kunci yang tersisa:

$$

$$K_3 = 448CC78CEF6A8D2243436915534831DB$$

$$

$$K_4 = 04FD9F0AC4ADEB1568ECCFE9D853453D$$

$$

$$K_5 = ACF129F44692E5D3285E4AC468646457$$

$$

$$K_6 = 1B58DA3428E832B532645C16359407BD$$

$$

$$K_7 = B198005A26275770DE45877E7540E651$$

$$

$$K_8 = 84F98622A2912AD73EDD9F7B0125795A$$

$$

$$K_9 = 17E5B6CD732FF3A52331C77853E244BB$$

$$

$$K_ {10} = 43404A8EA8BA5D755BF4BC1674DDE972$$

Blokir enkripsi

Kami menghitung semua kunci dan sekarang akhirnya kami dapat langsung menuju enkripsi blok teks dan jika Anda dengan cermat membaca semua yang ditulis di atas, maka mengenkripsi teks tidak akan sulit, karena semua operasi yang digunakan dalam proses ini dan urutannya telah diperiksa secara rinci.

Ambil blok plaintext:

$$

$$T = 8899AABBCCDDEEFF0077665544332211$$

jalankan urutan operasi X, S, L

$$

$$X (T, K_1) = FFFFFFFFFFFFFFFFFFFFFF99BB99FF99BB99$$

$$

$$S (X (T, K_1)) = B6B6B6B6B6B6B6B6B6E87DE8B6E87DE8$$

$$

$$L (S (X (T, K_1)))) = 30081449922F4ACFA1B055E386B697E2$$

$$

$$T_1 = 30081449922F4ACFA1B055E386B697E2$$

$$

$$X (T_1, K_2) = DFC5BFC0F56A69CEB18201951E0C4B1C$$

$$

$$S (X (T_1, K_2)) = 61AC3B07F47891E74524EE945F23A214$$

$$

$$L (S (X (T_1, K_2)))) = 7290C6A158426FB396D562087A495E28$$

$$

$$T_2 = 7290C6A158426FB396D562087A495E28$$

dan seterusnya, hasil akhirnya akan terlihat seperti ini:

$$

$$T_ {10} = CDEDD4B9428D465A3024BCBE909D677F$$

Blokir Dekripsi

Untuk mendekripsi teks, Anda perlu menggunakan operasi terbalik dalam urutan terbalik (lihat Gambar. 2).

Operasi XOR terbalik dengan dirinya sendiri, kebalikan dari operasi S adalah substitusi menurut tabel berikut:


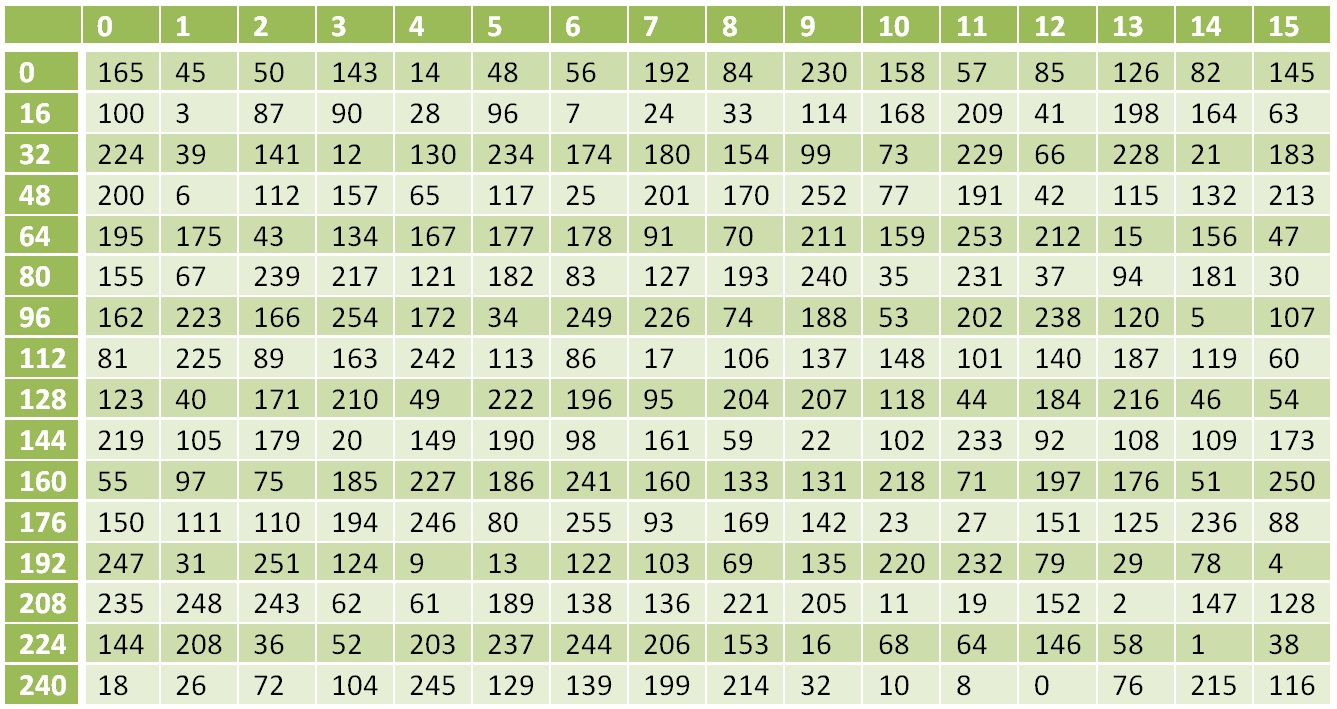Tabel Transformasi Nonlinear Terbalik

Transformasi terbalik ke fungsi L adalah:

$$

$$a_0 = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 + a_5 * 194 +$$

$$

$$+ a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

dan pergeseran ke arah level senior. (Ulangi operasi 16 kali)

Implementasi Java

Pertama, kita mendefinisikan konstanta yang diperlukan

static final int BLOCK_SIZE = 16; //   //     static final byte[] Pi = { (byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16, (byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D, (byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA, 0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1, (byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21, (byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F, 0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0, 0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F, (byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB, (byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC, (byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, (byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87, 0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7, (byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1, 0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E, 0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57, (byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9, (byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03, (byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC, (byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A, (byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41, (byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F, (byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B, 0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7, 0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89, (byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE, (byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61, 0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B, (byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52, 0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0, (byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6 }; //     static final byte[] reverse_Pi = { (byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0, 0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91, 0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F, (byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4, (byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7, (byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9, (byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5, (byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B, 0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F, (byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F, (byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E, (byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2, 0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B, 0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11, 0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C, 0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F, (byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36, (byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1, 0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD, 0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0, (byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA, (byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D, (byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58, (byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04, (byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88, (byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80, (byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE, (byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26, 0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7, (byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74 }; //    static final byte[] l_vec = { 1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1, (byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148 }; //     static byte[][] iter_C = new byte[32][16]; //     static byte[][] iter_key = new byte[10][64]; 

Mari kita buat semua fungsi utama:

 //  X static private byte[] GOST_Kuz_X(byte[] a, byte[] b) { int i; byte[] c = new byte[BLOCK_SIZE]; for (i = 0; i < BLOCK_SIZE; i++) c[i] = (byte) (a[i] ^ b[i]); return c; } //  S static private byte[] GOST_Kuz_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = Pi[data]; } return out_data; } 

Untuk mengimplementasikan fungsi L, kita membutuhkan beberapa fungsi bantu, satu untuk menghitung penggandaan angka di bidang Galois, dan satu untuk shift.

 //     static private byte GOST_Kuz_GF_mul(byte a, byte b) { byte c = 0; byte hi_bit; int i; for (i = 0; i < 8; i++) { if ((b & 1) == 1) c ^= a; hi_bit = (byte) (a & 0x80); a <<= 1; if (hi_bit < 0) a ^= 0xc3; // x^8+x^7+x^6+x+1 b >>= 1; } return c; } //  R     ,    L- static private byte[] GOST_Kuz_R(byte[] state) { int i; byte a_15 = 0; byte[] internal = new byte[16]; for (i = 15; i >= 0; i--) { if(i == 0) internal[15] = state[i]; else internal[i - 1] = state[i]; a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]); } internal[15] = a_15; return internal; } static private byte[] GOST_Kuz_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal = in_data; for (i = 0; i < 16; i++) { internal = GOST_Kuz_R(internal); } out_data = internal; return out_data; } 

Fungsi terbalik:

 //  S^(-1) static private byte[] GOST_Kuz_reverse_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = reverse_Pi[data]; } return out_data; } static private byte[] GOST_Kuz_reverse_R(byte[] state) { int i; byte a_0; a_0 = state[15]; byte[] internal = new byte[16]; for (i = 1; i < 16; i++) { internal[i] = state[i - 1]; a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]); } internal[0] = a_0; return internal; } static private byte[] GOST_Kuz_reverse_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal; internal = in_data; for (i = 0; i < 16; i++) internal = GOST_Kuz_reverse_R(internal); out_data = internal; return out_data; } //    static private void GOST_Kuz_Get_C() { int i; byte[][] iter_num = new byte[32][16]; for (i = 0; i < 32; i++) { for(int j = 0; j < BLOCK_SIZE; j++) iter_num[i][j] = 0; iter_num[i][0] = (byte) (i+1); } for (i = 0; i < 32; i++) { iter_C[i] = GOST_Kuz_L(iter_num[i]); } } // ,     static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const) { byte[] internal; byte[] out_key_2 = in_key_1; internal = GOST_Kuz_X(in_key_1, iter_const); internal = GOST_Kuz_S(internal); internal = GOST_Kuz_L(internal); byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2); byte key[][] = new byte[2][]; key[0] = out_key_1; key[1] = out_key_2; return key; } //     public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2) { int i; byte[][] iter12 = new byte[2][]; byte[][] iter34 = new byte[2][]; GOST_Kuz_Get_C(); iter_key[0] = key_1; iter_key[1] = key_2; iter12[0] = key_1; iter12[1] = key_2; for (i = 0; i < 4; i++) { iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]); iter_key[2 * i + 2] = iter12[0]; iter_key[2 * i + 3] = iter12[1]; } } //    public byte[] GOST_Kuz_Encript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; for(i = 0; i < 9; i++) { out_blk = GOST_Kuz_X(iter_key[i], out_blk); out_blk = GOST_Kuz_S(out_blk); out_blk = GOST_Kuz_L(out_blk); } out_blk = GOST_Kuz_X(out_blk, iter_key[9]); return out_blk; } //   public byte[] GOST_Kuz_Decript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; out_blk = GOST_Kuz_X(out_blk, iter_key[9]); for(i = 8; i >= 0; i--) { out_blk = GOST_Kuz_reverse_L(out_blk); out_blk = GOST_Kuz_reverse_S(out_blk); out_blk = GOST_Kuz_X(iter_key[i], out_blk); } return out_blk; } 

Nah, dan fungsi utamanya

 static byte[] key_1 = {0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee, (byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88}; static byte[] key_2 = {(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01, 0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe}; static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211"); public static void main(String[] args) { GOST_Kuz_Expand_Key(key_1, key_2); byte[] encriptBlok = GOST_Kuz_Encript(blk); System.out.println(DatatypeConverter.printHexBinary(encriptBlok)); byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok); System.out.println(DatatypeConverter.printHexBinary(decriptBlok)); } 

Kami belajar mengenkripsi blok data untuk mengenkripsi teks yang panjangnya lebih panjang dari panjang blok, ada beberapa mode yang dijelaskan dalam standar - GOST 34.13-2015:

• mode penggantian sederhana (Electronic Codebook, ECB);
• mode gamma (Penghitung, RKT);
• mode gamma dengan umpan balik keluaran (Output Umpan Balik, OFB);
• mode penggantian gearing sederhana (Cipher Block Chaining, CBC);
• mode gamma dengan umpan balik dalam ciphertext (Cipher Feedback, CFB);
• Mode Kode Otentikasi Pesan (MAC).

Dalam semua mode, panjang teks harus selalu kelipatan dari panjang blok, sehingga teks selalu empuk ke kanan dengan satu bit tunggal dan nol untuk panjang blok.

Mode termudah adalah mode penggantian sederhana. Dalam mode ini, teks dibagi menjadi beberapa blok, lalu setiap blok dienkripsi secara terpisah dari yang lainnya, lalu blok-blok teks sandi dilem bersama dan kami mendapatkan pesan terenkripsi. Mode ini adalah yang paling sederhana dan paling rentan dan hampir tidak pernah diterapkan dalam praktik.

Mode lain dapat dipertimbangkan secara rinci nanti.