Struktur data B-tree

Halo semuanya! Kami meluncurkan set baru untuk kursus "Algoritma untuk Pengembang" dan hari ini kami ingin berbagi terjemahan menarik yang disiapkan untuk siswa kursus ini.



Dalam pohon pencarian, seperti pohon pencarian biner, pohon AVL, pohon merah-hitam, dll. setiap node hanya berisi satu nilai (kunci) dan maksimum dua turunan. Namun, ada jenis khusus pohon pencarian yang disebut B-tree (diucapkan Bi-tree). Di dalamnya, simpul berisi lebih dari satu nilai (kunci) dan lebih dari dua keturunan. B-tree dikembangkan pada tahun 1972 oleh Bayer dan McCraith dan disebut Pohon Pencarian m-arah Tinggi Seimbang . Nama modernnya B-tree diterima kemudian.

B-tree dapat didefinisikan sebagai berikut:
B-tree adalah pohon pencarian seimbang di mana setiap node berisi banyak kunci dan memiliki lebih dari dua anak.

Di sini, jumlah kunci dalam simpul dan jumlah turunannya tergantung pada urutan pohon-B. Setiap B-tree memiliki pesanan.

B-tree of order m memiliki properti berikut:

Properti 1: Kedalaman semua daun adalah sama.
Properti 2: Semua node kecuali root harus memiliki setidaknya (m / 2) - 1 kunci dan maksimum kunci m-1 .
Properti 3: Semua node tanpa daun, kecuali root (mis., Semua node internal), harus memiliki minimum m / 2 turunan.
Properti 4: Jika root adalah simpul tanpa daun, ia harus memiliki setidaknya 2 keturunan.
Properti 5: Sebuah simpul tanpa daun dengan kunci n-1 harus memiliki n anak.
Properti 6: Semua kunci di simpul harus diatur dalam urutan nilainya.

Sebagai contoh, 4-order B-tree berisi maksimum 3 nilai kunci dan maksimum 4 anak untuk setiap node.


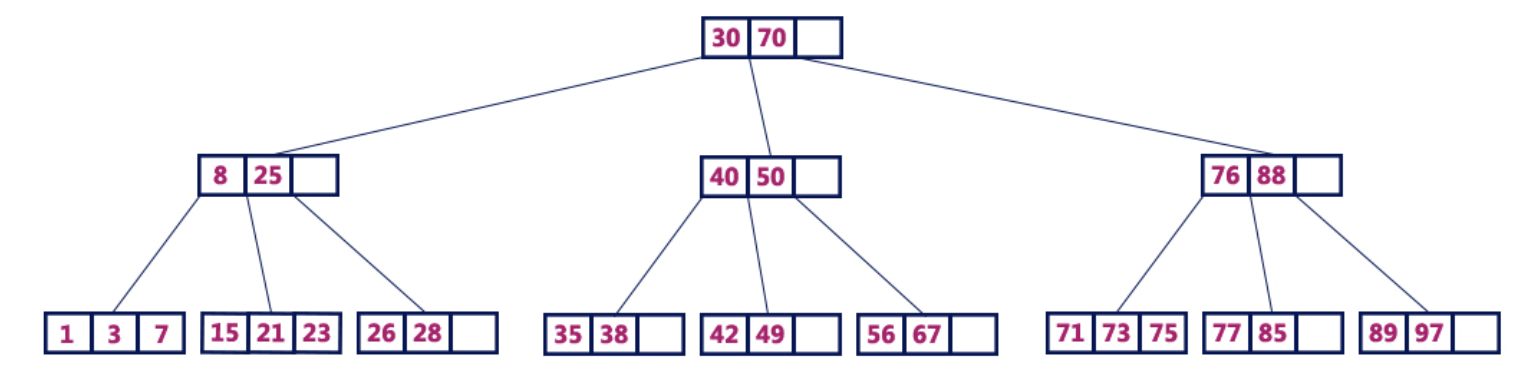B-tree 4 pesanan

Operasi B-tree

Operasi berikut dapat dilakukan pada B-tree:

1. Cari
2. Masukkan
3. Hapus

Cari B-tree

Pencarian B-tree mirip dengan pencarian binary-tree. Di pohon pencarian biner, pencarian dimulai dari root dan setiap kali keputusan dua arah dibuat (berjalan di sepanjang subtree kiri atau kanan). Dalam B-tree, pencarian juga dimulai dari simpul root, tetapi pada setiap langkah keputusan n-sided dibuat, di mana n adalah jumlah total keturunan dari simpul yang dimaksud. Dalam B-tree, kompleksitas pencarian adalah O (log n) . Pencariannya adalah sebagai berikut:

Langkah 1: Baca item yang akan dicari.
Langkah 2: Bandingkan item yang dicari dengan nilai kunci pertama di simpul akar pohon.
Langkah 3: Jika cocok, cetak: "Node ditemukan!" dan selesaikan pencarian.
Langkah 4: Jika tidak cocok, periksa nilai item lebih atau kurang dari nilai kunci saat ini.
Langkah 5: Jika item yang Anda cari lebih kecil, lanjutkan mencari subtree kiri.
Langkah 6: Jika item pencarian lebih besar, bandingkan item dengan nilai kunci berikutnya dalam node dan ulangi Langkah 3, 4, 5 dan 6 sampai kecocokan ditemukan atau sampai item pencarian dibandingkan dengan nilai kunci terakhir pada node sheet.
Langkah 7: Jika nilai kunci terakhir dalam daftar node tidak cocok dengan pencarian, cetak "Item tidak ditemukan!" dan selesaikan pencarian.

Operasi penyisipan B-tree

Di pohon-B, item baru hanya dapat ditambahkan ke simpul daun. Ini berarti bahwa pasangan nilai kunci baru selalu ditambahkan hanya ke simpul daun. Sisipan adalah sebagai berikut:

Langkah 1: Periksa apakah pohon kosong.
Langkah 2: Jika pohon kosong, buat simpul baru dengan nilai kunci baru dan anggap sebagai simpul root.
Langkah 3: Jika pohon tidak kosong, cari simpul daun yang cocok yang akan ditambahkan nilai baru menggunakan logika pohon pencarian biner.
Langkah 4: Jika ada sel kosong di simpul daun saat ini, tambahkan nilai kunci baru ke simpul daun saat ini, mengikuti urutan peningkatan nilai kunci di dalam simpul.
Langkah 5: Jika simpul saat ini penuh dan tidak memiliki sel bebas, pisahkan simpul daun dengan mengirimkan nilai rata-rata ke simpul induk. Ulangi langkah ini sampai nilai yang akan dikirim dikomit ke node.
Langkah 6: Jika pemisahan terjadi dengan akar pohon, maka rata-rata menjadi akar baru pohon dan ketinggian pohon bertambah satu.

Contoh:

Mari kita membuat pohon-B dari urutan 3 dengan menambahkan angka dari 1 hingga 10 di dalamnya.

Masukkan (1):
Karena "1" adalah elemen pertama dari pohon, itu dimasukkan ke dalam simpul baru dan simpul ini menjadi akar dari pohon.



Sisipkan (2):
Elemen 2 ditambahkan ke simpul daun yang ada. Sekarang kita hanya memiliki satu simpul, oleh karena itu keduanya merupakan akar dan daun sekaligus. Lembar ini memiliki sel kosong. Lalu "2" masuk ke sel kosong ini.



Masukkan (3):
Elemen 3 ditambahkan ke simpul daun yang ada. Sekarang kita hanya memiliki satu simpul, yaitu akar dan daun. Lembar ini tidak memiliki sel kosong. Oleh karena itu, kami memisahkan simpul ini dengan mengirimkan nilai rata-rata (2) ke simpul induk. Namun, simpul saat ini tidak memiliki simpul induk. Oleh karena itu, nilai rata-rata menjadi simpul akar pohon.



Masukkan (4):
Elemen "4" lebih besar dari simpul akar dengan nilai "2", sedangkan simpul akar bukan daun. Oleh karena itu, kami bergerak di sepanjang subtree kanan "2". Kami datang ke simpul daun dengan nilai "3", yang memiliki sel kosong. Jadi, kita bisa memasukkan elemen "4" ke dalam sel kosong ini.



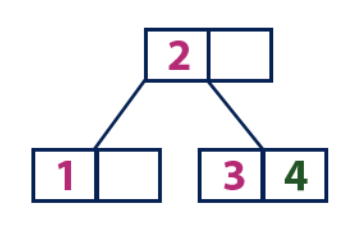Sisipkan (5):
Elemen "5" lebih besar dari simpul akar dengan nilai "2", sedangkan simpul akar bukan daun. Oleh karena itu, kami bergerak di sepanjang subtree kanan "2". Kami datang ke simpul daun dan menemukan bahwa itu sudah penuh dan tidak memiliki sel kosong. Kemudian kami membagi simpul ini dengan mengirimkan nilai rata-rata (4) ke simpul induk (2). Simpul induk memiliki sel kosong untuknya, sehingga nilai "4" ditambahkan ke simpul yang sudah ada nilai "2", dan elemen baru "5" ditambahkan sebagai lembar baru.



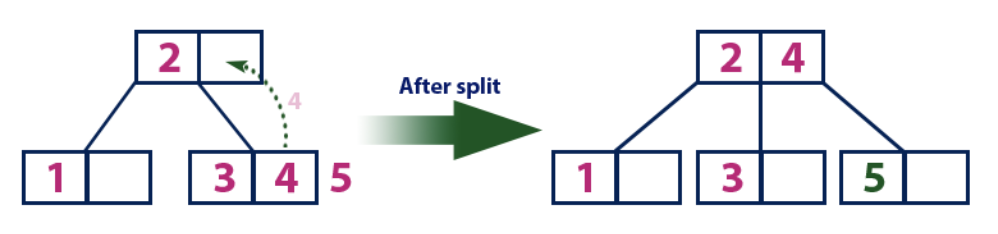Masukkan (6):
Elemen "6" lebih besar dari elemen root "2" dan "4", yang bukan daun. Kami bergerak di sepanjang subtree kanan elemen "4". Kami mencapai selembar dengan nilai "5", yang memiliki sel kosong, sehingga elemen "6" ditempatkan tepat di dalamnya.



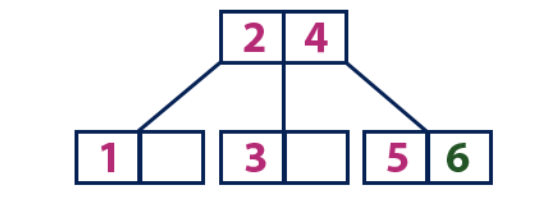Sisipkan (7):
Elemen "7" lebih besar dari elemen root "2" dan "4", yang bukan daun. Kami bergerak di sepanjang subtree kanan elemen "4". Kami mencapai simpul daun dan melihat bahwa itu penuh. Kami membagi simpul ini dengan mengirimkan nilai rata-rata "6" hingga simpul induk dengan elemen "2" dan "4". Namun, simpul induk juga penuh, jadi kami membagi simpul dengan elemen "2" dan "4", mengirimkan nilai "4" ke simpul induk. Hanya simpul ini belum ada di sana. Dalam kasus ini, simpul dengan elemen "4" menjadi root baru dari pohon.



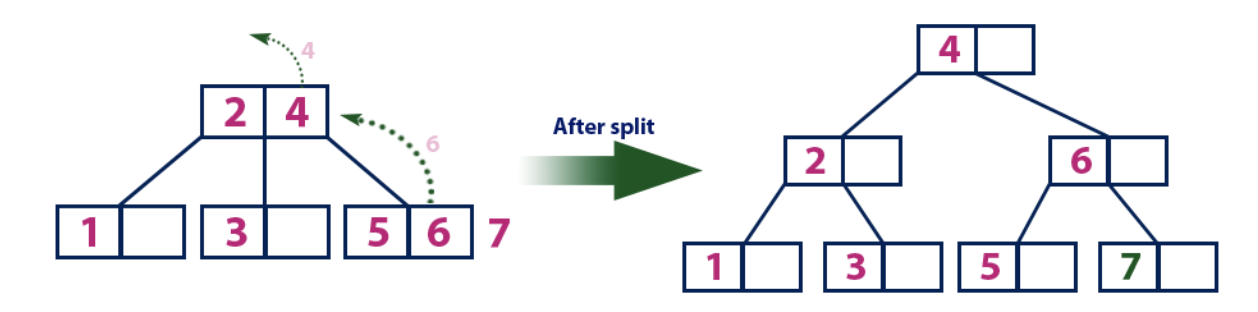Sisipkan (8):
Elemen 8 lebih besar dari simpul akar dengan nilai 4, dan simpul akar bukan daun. Kami bergerak sepanjang subtree kanan dari elemen "4" dan sampai ke node dengan nilai "6". "8" lebih besar dari "6" dan simpul dengan elemen "6" bukan selembar, jadi kami bergerak di sepanjang subtree kanan "6". Kami mencapai simpul daun dengan "7", yang memiliki sel kosong, jadi kami menempatkan "8" di dalamnya.



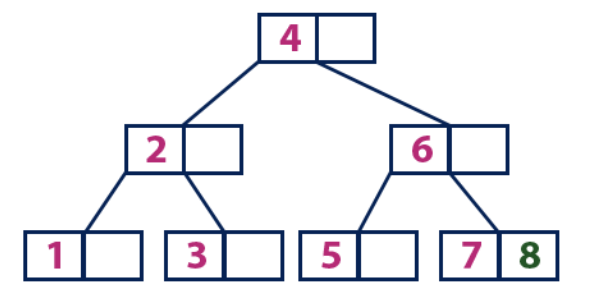Sisipkan (9):
Elemen 9 lebih besar dari simpul akar dengan nilai 4, dan simpul akar bukan daun. Kami bergerak sepanjang subtree kanan dari elemen "4" dan sampai ke node dengan nilai "6". "9" lebih besar dari "6" dan simpul dengan elemen "6" bukan lembar, jadi kami bergerak di sepanjang subtree kanan "6". Kami mencapai simpul daun dengan nilai "7" dan "8". Dia penuh. Kami membagi simpul ini dengan mengirimkan nilai rata-rata (8) ke simpul induk. Node induk "6" memiliki sel kosong, jadi kami menaruh "8" di dalamnya. Dalam hal ini, elemen baru "9" ditambahkan ke daftar node.



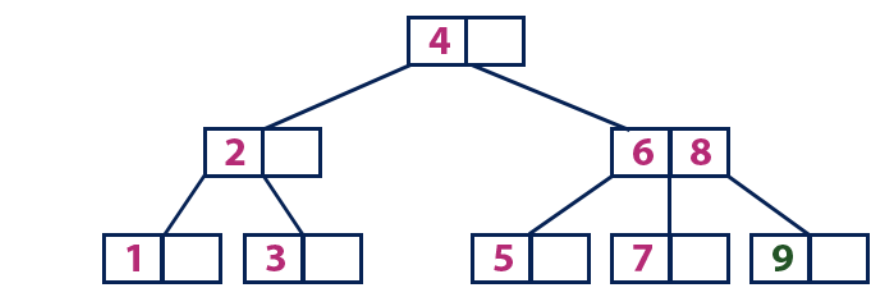
Sisipkan (10):
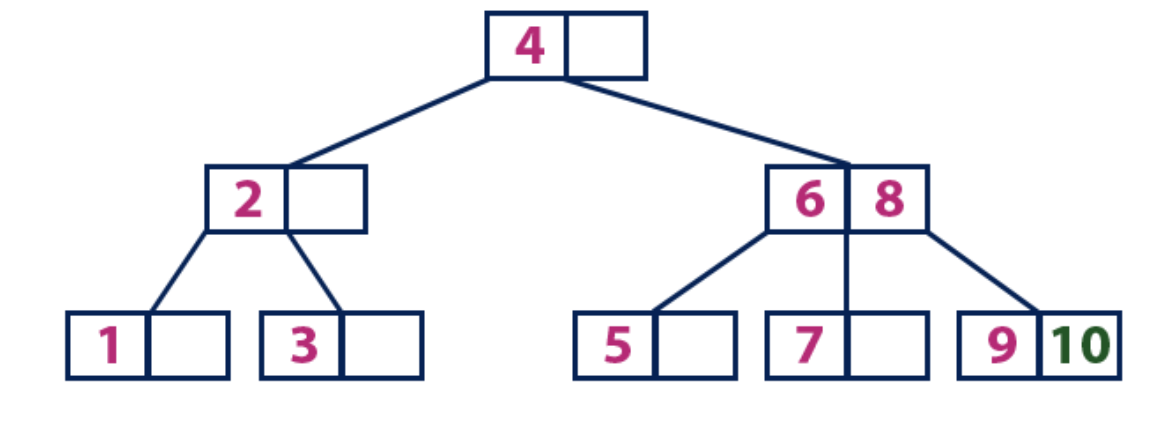
Elemen "10" lebih besar dari simpul akar dengan nilai "4", sedangkan simpul akar bukan daun. Kami bergerak di sepanjang subtree kanan elemen "4" dan sampai ke node dengan nilai "6" dan "8". "10" lebih besar dari "6" dan "8" dan simpul dengan elemen-elemen ini bukan selembar, jadi kami bergerak di sepanjang subtree kanan "8". Kami mencapai simpul daun dengan nilai "9". Dia memiliki sel kosong, jadi kami menempatkan "10" di sana.



Kami menyarankan Anda memahami secara mandiri dalam praktik bagaimana pohon-B disusun menggunakan visualisasi ini .

Kami sedang menunggu semua orang pada pelajaran terbuka gratis , yang akan diadakan pada 12 Juli. Sampai ketemu lagi!