Berhenti menggunakan RSA

Hai% nama pengguna%!

RSA adalah algoritma kriptografi asimetris yang banyak digunakan pertama yang masih populer di industri. Sekilas relatif sederhana. Enkripsi dan tanda tangan RSA dapat dihitung pada selembar kertas, yang sering dilakukan siswa dalam pekerjaan laboratorium.
Tetapi ada banyak sekali nuansa yang tanpanya bahkan seorang anak pun dapat memecahkan implementasi RSA Anda.

Untuk beberapa alasan, orang masih berpikir RSA adalah algoritma yang baik. Tetapi pada kenyataannya, ruang lingkup untuk tembakan di kaki ketika menerapkan RSA sangat besar. Parameter yang lemah sulit untuk diverifikasi, jika bukan tidak mungkin. Dan buruknya kinerja algoritma mendorong pengembang untuk menggunakan cara-cara berisiko untuk memperbaikinya.

Lebih buruk lagi, padding serangan oracle yang ditemukan lebih dari 20 tahun yang lalu masih relevan saat ini.
Sekalipun secara teori dimungkinkan untuk mengimplementasikan RSA dengan benar, dalam praktiknya "prestasi" seperti itu hampir mustahil untuk dicapai. Dan kerentanan yang terus muncul selama beberapa dekade hanya menegaskan hal ini.

Beberapa kata tentang algoritma RSA

Jika Anda tahu cara kerja RSA, Anda dapat melewati bagian ini.

RSA adalah cryptosystem kunci publik yang memiliki dua kegunaan.

Yang pertama adalah enkripsi, ketika Alice menerbitkan kunci publiknya dan Bob, mengetahuinya, dapat mengenkripsi pesan yang hanya dapat dibaca oleh Alice, mendekripsi dengan kunci pribadinya.

Yang kedua adalah tanda tangan digital, yang memungkinkan Alice untuk menandatangani pesan dengan kunci pribadinya sehingga semua orang dapat memverifikasi tanda tangan ini dengan kunci publiknya.

Kedua algoritma berbeda dalam detail yang tidak signifikan, oleh karena itu kami akan menyebutnya hanya RSA.

Untuk mulai bekerja dengan RSA, Alice perlu memilih dua bilangan prima p dan q , yang bersama-sama membentuk sekelompok angka modulo N = pq . Maka Alice perlu memilih eksponen terbuka dan eksponen rahasia sedemikian rupa $$$ed = 1 \ mod (p-1) (q-1)$. Intinya, e dan d harus saling sederhana.

Setelah opsi ini dipilih, Bob dapat mengirim pesan kepada Alice, komputasi $$$C = M ^ e (mod \ N)$. Alice kemudian dapat mendekripsi pesan dengan komputasi $$$M = C ^ d (mod \ N)$.
Tanda tangan digital justru sebaliknya. Jika Alice ingin menandatangani pesan, dia menghitung tanda tangannya $$$S = M ^ d (mod \ N)$Bob dapat memeriksa dengan memastikan pesannya $$$M = S ^ e (mod \ N)$

Itu saja, itu ide utamanya. Kami akan kembali ke Padding oracles nanti, tetapi untuk sekarang mari kita lihat apa yang dapat dilakukan jika parameter RSA dipilih secara tidak benar.

Awal dari akhir

Agar RSA berfungsi, Anda perlu memilih beberapa parameter. Sayangnya, metode yang tampaknya tidak bersalah dari pilihan mereka dapat membahayakan keamanan. Mari kita telusuri masing-masing dan melihat kejutan yang tidak menyenangkan menunggu Anda.

Generasi Perdana

Keamanan RSA didasarkan pada fakta bahwa memiliki sejumlah besar N , yang merupakan produk dari dua bilangan prima p dan q , menguraikan N menjadi faktor utama tanpa mengetahui p dan q sulit dilakukan. Pengembang bertanggung jawab untuk memilih bilangan prima yang membentuk modul RSA. Proses ini sangat lambat dibandingkan dengan pembuatan kunci untuk protokol kriptografi lainnya, di mana cukup untuk hanya memilih beberapa byte acak. Oleh karena itu, alih-alih menghasilkan bilangan prima yang benar-benar acak, pengembang sering mencoba membuat angka dengan bentuk tertentu. Hampir selalu berakhir dengan buruk. Ada banyak cara untuk memilih bilangan prima sehingga anjak N sederhana. Misalnya, p dan q harus unik secara global. Jika p atau q pernah digunakan kembali dalam modul RSA lainnya, maka kedua faktor dapat dengan mudah dihitung menggunakan algoritma GCD. Generator angka acak yang buruk membuat skenario ini sangat mungkin, dan penelitian telah menunjukkan bahwa sekitar 1% dari lalu lintas TLS pada tahun 2012 terkena serangan semacam itu.

Selain itu, p dan q harus dipilih secara independen satu sama lain. Jika p dan q berbagi sekitar setengah dari bit yang paling signifikan, maka N dapat dihitung menggunakan metode Fermat. Bahkan, bahkan memilih algoritma pengujian kesederhanaan dapat memiliki implikasi keamanan. Mungkin serangan yang paling banyak dipublikasikan adalah kerentanan ROCA di RSALib, yang memengaruhi banyak kartu pintar, modul platform tepercaya, dan bahkan kunci Yubikey. Di sini, saat membuat kunci, hanya bilangan prima dari formulir tertentu yang digunakan untuk mempercepat perhitungan. Bilangan prima yang dihasilkan dengan cara ini sepele untuk ditemukan dengan menggunakan teknik rumit dalam teori bilangan. Setelah sistem yang lemah telah dikenali, sifat aljabar khusus dari bilangan prima memungkinkan penyerang untuk menggunakan metode Coppersmith untuk menguraikan N.

Harus diingat bahwa dalam semua kasus ini, generasi bilangan prima dengan cara ini adalah fakta yang jelas mengarah pada kegagalan sistem secara total. Ini karena sifat bilangan-teori yang tidak signifikan dari bilangan prima memiliki dampak signifikan terhadap keamanan RSA. Harapan bahwa pengembang biasa akan menavigasi ladang ranjau matematis ini secara serius merusak keamanan.

Peserta pameran rahasia d

Karena penggunaan kunci pribadi yang besar secara negatif mempengaruhi waktu dekripsi dan penandatanganan, pengembang memiliki insentif untuk memilih huruf d kecil, terutama dalam hal perangkat dengan konsumsi daya yang rendah, seperti kartu pintar. Namun, seorang penyerang dapat memulihkan kunci pribadi ketika d kurang dari tingkat 4 root N. Sebagai gantinya, pengembang harus memilih nilai d yang besar , sehingga teorema sisa China dapat digunakan untuk mempercepat dekripsi. Namun, kompleksitas dari pendekatan ini meningkatkan kemungkinan kesalahan implementasi minor yang dapat menyebabkan pemulihan utama.

Anda mengatakan bahwa biasanya selama inisialisasi RSA Anda pertama kali menghasilkan modul, menggunakan eksponen terbuka tetap, dan kemudian memilih rahasia?
Ya, ini mencegah serangan dengan eksponen rahasia kecil jika Anda selalu menggunakan salah satu eksponen terbuka yang direkomendasikan e .
Sayangnya, ini juga mengasumsikan bahwa pengembang akan benar-benar melakukan ini. Di dunia nyata, pengembang sering melakukan hal-hal aneh, misalnya, pertama memilih d dan kemudian mempertimbangkan e .

Open Exhibitor e

Seperti halnya peserta pameran rahasia, pengembang ingin menggunakan peserta pameran terbuka kecil untuk menghemat enkripsi dan verifikasi tanda tangan. Biasanya, bilangan prima Fermat digunakan dalam konteks ini, khususnya e = 3, 17 dan 65537.

Terlepas dari kenyataan bahwa kriptografi merekomendasikan penggunaan 65537, pengembang sering memilih e = 3, yang menyebabkan banyak kerentanan dalam kriptosistem RSA.


(Di sini, pengembang menggunakan e = 1, yang sebenarnya tidak mengenkripsi plaintext sama sekali.)

Ketika e = 3 atau ukuran yang serupa, banyak yang bisa salah. Eksponen terbuka kecil sering dikombinasikan dengan kesalahan umum lainnya yang memungkinkan penyerang untuk mendekripsi ciphertext atau faktor N.

Sebagai contoh, serangan Franklin-Reuters memungkinkan penyerang untuk mendekripsi dua pesan yang dihubungkan oleh jarak yang diketahui dan diperbaiki. Dengan kata lain, misalkan Alice mengirim Bob hanya "membeli" atau "menjual". Pesan-pesan ini akan dikaitkan dengan nilai yang diketahui dan akan memungkinkan penyerang untuk menentukan mana dari mereka yang berarti "beli" dan yang "jual" tanpa mendekripsi pesan tersebut. Beberapa serangan dengan e kecil bahkan dapat menyebabkan pemulihan kunci.

Jika eksponen terbuka kecil (tidak hanya 3), penyerang yang mengetahui beberapa bit kunci rahasia dapat memulihkan bit yang tersisa dan memecahkan cryptosystem. Meskipun banyak dari serangan RSA e = 3 ini dapat diperbaiki dengan padding, pengembang yang mengimplementasikan RSA sendiri sering lupa untuk menggunakannya.

Tanda tangan RSA juga rentan terhadap peserta pameran publik kecil. Pada tahun 2006, Bleichenbacher menemukan serangan yang memungkinkan penyerang untuk menandatangani tanda tangan sewenang-wenang palsu di banyak implementasi RSA, termasuk yang digunakan di Firefox dan Chrome. Ini berarti bahwa setiap sertifikat TLS dari implementasi yang rentan dapat dirusak. Serangan ini mengeksploitasi fakta bahwa banyak perpustakaan menggunakan eksponen publik kecil dan tidak melakukan pemeriksaan penyelarasan sederhana saat memproses tanda tangan RSA. Serangan Bleichenbacher pada tanda tangan sangat sederhana sehingga termasuk dalam banyak latihan dalam kursus kriptografi.

Memilih opsi adalah tugas yang sulit

Yang umum dari semua serangan pada parameter ini adalah jumlah total varian yang mungkin dari parameter jauh lebih besar daripada jumlah varian yang aman.

Diasumsikan bahwa pengembang sendiri akan mengelola proses seleksi yang kompleks ini, karena semuanya kecuali eksponen terbuka harus dihasilkan selama inisialisasi.
Tidak ada cara mudah untuk memeriksa keandalan parameter . Sebaliknya, pengembang membutuhkan basis matematika yang serius, yang kehadirannya tidak boleh diharapkan dari karyawan biasa. Meskipun menggunakan RSA dengan penyelarasan dapat menyelamatkan Anda jika Anda memiliki parameter yang salah, banyak yang memilih untuk tidak melakukannya.

Padding serangan Oracle

Seperti yang kami jelaskan di atas, cukup menggunakan RSA di luar kotak tidak cukup berhasil. Misalnya, skema RSA yang diuraikan dalam pendahuluan akan membuat ciphertext yang identik jika plaintext yang sama pernah dienkripsi lebih dari satu kali. Ini adalah masalah karena itu akan memungkinkan penyerang mempelajari isi pesan dari konteks, tanpa bisa mendekripsi. Inilah sebabnya mengapa kita perlu menyelaraskan pesan dengan beberapa byte acak. Sayangnya, skema penyelarasan yang paling banyak digunakan, PKCS # 1 v1.5, sering rentan terhadap apa yang disebut padding oracle attack.

Serangan awal pada PKCS # 1 v1.5 ditemukan kembali pada tahun 1998 oleh Daniel Bleikhanbacher. Terlepas dari kenyataan bahwa ia berusia lebih dari 20 tahun, hari ini ia terus relevan untuk banyak sistem. Versi modern dari serangan ini sering menyertakan oracle tambahan, sedikit lebih kompleks daripada yang awalnya dijelaskan oleh Bleikhanbacher, misalnya, waktu respons server atau pelaksanaan downgrade protokol apa pun di TLS. Salah satu contoh yang mengejutkan adalah serangan ROBOT , yang sangat mengerikan sehingga tim peneliti dapat menandatangani pesan dengan kunci rahasia Facebook dan PayPal. Beberapa mungkin berpendapat bahwa ini bukan kesalahan RSA - matematika dasar baik-baik saja, orang hanya mengacaukan standar penting beberapa dekade yang lalu. Faktanya adalah bahwa kita sudah memiliki , sejak 1998, skema penyelarasan standar dengan bukti keamanan yang ketat, OAEP. Tapi hampir tidak ada yang menggunakannya. Bahkan ketika ini terjadi, sudah menjadi rahasia umum bahwa OAEP sulit untuk diimplementasikan, dan seringkali rentan terhadap serangan Manger, yang merupakan serangan oracle lain yang dapat digunakan untuk memulihkan plaintext.

Masalah mendasar di sini adalah bahwa penyelarasan diperlukan saat menggunakan RSA, dan kompleksitas tambahan ini membuka ruang lingkup besar untuk serangan terhadap cryptosystem. Fakta bahwa satu bit informasi, “apakah pesannya telah diselaraskan dengan benar”, dapat memiliki dampak besar pada keamanan yang membuat pengembangan perpustakaan yang aman secara praktis tidak mungkin dilakukan. TLS 1.3 tidak lagi mendukung RSA, jadi kami dapat mengharapkan lebih sedikit serangan seperti itu di masa depan.

Tetapi sementara pengembang terus menggunakan RSA dalam aplikasi mereka sendiri, serangan Padding Oracle akan terus terjadi.

Apa yang harus dilakukan

Orang sering lebih suka menggunakan RSA karena mereka merasa secara konseptual lebih sederhana daripada protokol DSA yang berbelit-belit atau kriptografi kurva eliptik (ECC). Tetapi meskipun RSA lebih intuitif, itu benar-benar tidak memiliki perlindungan dari si bodoh.

Pertama-tama, kesalahpahaman umum adalah bahwa elips sangat berbahaya, karena memilih kurva yang buruk dapat membatalkan semuanya. Memang benar bahwa pemilihan kurva memiliki dampak besar pada keamanan, tetapi salah satu manfaat menggunakan ECC adalah pemilihan parameter dapat dilakukan secara publik. Cryptographers membuat pilihan parameter untuk Anda, jadi pengembang hanya perlu membuat byte data acak untuk digunakan sebagai kunci. Pengembang secara teoritis dapat membangun implementasi ECC dengan parameter yang mengerikan dan tidak akan dapat memeriksa hal-hal seperti titik kurva yang salah, tetapi biasanya tidak. Penjelasan yang mungkin adalah bahwa matematika di balik ECC sangat kompleks sehingga sangat sedikit orang merasa cukup percaya diri untuk mengimplementasikannya. Dengan kata lain, ketakutan ini memaksa orang untuk menggunakan perpustakaan yang dibuat oleh cryptographers yang tahu barang-barang mereka. RSA, di sisi lain, sangat sederhana sehingga dapat (buruk) diimplementasikan dalam satu jam.

Kedua, pencocokan kunci atau skema tanda tangan berbasis Diffie-Hellman (termasuk opsi kurva eliptik) tidak memerlukan perataan dan, karenanya, sepenuhnya tahan terhadap serangan Oracle Padding. Ini adalah kemenangan besar, mengingat RSA memiliki rekam jejak yang sangat panjang untuk menghindari kelas kerentanan ini.

Kami merekomendasikan penggunaan Curve25519 untuk pertukaran kunci dan ed25519 untuk tanda tangan digital. Enkripsi harus dilakukan menggunakan protokol ECIES, yang menggabungkan pertukaran kunci ECC dengan algoritma enkripsi simetris. Curve25519 dirancang untuk sepenuhnya mencegah kelas serangan yang mungkin terjadi pada kurva lain, dan itu juga sangat cepat. Selain itu, ini diterapkan di banyak perpustakaan, misalnya libsodium, yang dilengkapi dengan dokumentasi yang mudah dibaca dan tersedia dalam sebagian besar bahasa.

Berhenti menggunakan RSA. Serius.

(Twilio masih menggunakan kunci RSA)


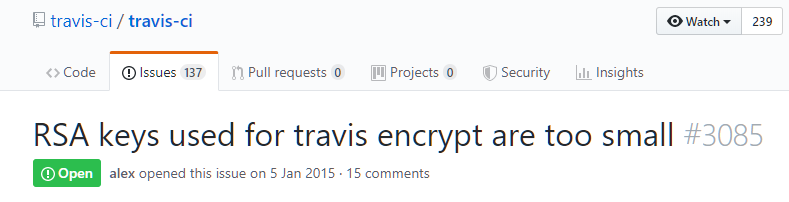
(Travis CI masih menggunakan kunci 1024 bit dan tidak memungkinkan untuk menggantinya)

RSA adalah tonggak penting dalam pengembangan komunikasi yang aman, tetapi dua dekade terakhir penelitian kriptografi telah membuatnya usang. Algoritma pada kurva eliptik untuk pertukaran kunci dan tanda tangan digital telah distandarisasi pada tahun 2005 dan sejak itu telah diintegrasikan ke dalam perpustakaan yang intuitif dan tahan terhadap penyalahgunaan, seperti libsodium. Fakta bahwa RSA masih banyak digunakan saat ini menunjukkan kedua kesalahan pada bagian cryptographers karena deskripsi yang tidak memadai dari risiko yang melekat dalam RSA dan pengembang yang melebih-lebihkan kemampuan mereka untuk berhasil menyebarkannya. Komunitas keamanan harus mulai menganggapnya sebagai masalah kawanan - walaupun beberapa dari kita mungkin dapat menavigasi proses yang sangat berbahaya dalam mengatur atau mengimplementasikan RSA, pengecualian membuat jelas bagi pengembang bahwa RSA masih relevan dalam beberapa hal. Meskipun banyak peringatan dan peringatan di StackExchange dan GitHub README, sangat sedikit orang yang percaya bahwa merekalah yang akan merusak RSA, dan oleh karena itu mereka terus bertindak dengan ceroboh. Pada akhirnya, pengguna Anda akan membayar untuk itu. Itu sebabnya kita semua harus setuju bahwa menggunakan RSA pada 2019 benar-benar tidak dapat diterima. Tidak ada pengecualian.

Artikel asli dalam bahasa Inggris.

VirgilSecurity, Inc. Mengembangkan SDK yang ramah bagi pengembang open source dan layanan perlindungan data. Kami mengizinkan pengembang untuk menggunakan algoritma yang ada dengan risiko keamanan minimal.

PS Saya sarankan Anda juga membaca tentang menanamkan backdoor di kunci publik RSA.