Sebuah model deret angka dan unsur-unsurnya. Belah ketupat

   

Dalam karya ini, model dasar G2 ^± dipertahankan, tetapi organisasi sel yang berbeda diterima (gambar lain). Di atas kisi utama dengan sel 1 × 1 , kotak yang lebih besar diwakili - kotak rhombus, dan juga kotak pusat rhombus dipertimbangkan (SCR). Grid terakhir tidak digambarkan agar tidak membebani garis dengan pola dengan belah ketupat. Kami tidak akan mengulangi definisi dan konsep yang dijelaskan secara rinci dalam karya - karya sebelumnya , tetapi memberikan tautan yang menunjuk ke karya-karya ini.

Deskripsi model konstruktif

Melalui sel-sel G2 ±-model yang terdapat pada diagonal D _i bahkan panjang dan K _i pendek dengan angka-angka yang berakhir dengan nol dalam submodel G2, garis-garis ditarik yang membentuk jaringan besar dari belah ketupat di dalam pesawat. Wilayah belah ketupat untuk sel secara kolektif menutupi seluruh bidang tanpa celah. Setiap belah ketupat mengandung 41 sel, yang hanya 16 yang menarik, dan ketika menggali sebuah belah ketupat, hanya 4 sel dengan fleksi tetap yang digunakan.

Karakteristik belah ketupat akan meliputi:

• jumlah sel dalam belah ketupat;
• nilai angka di sel pusat;
• angka horisontal ( N _i ) dan vertikal ( V _i );
• mengidentifikasi sel untuk angka dengan infleksi 1, 3, 7, 9;
• koordinat sel-sel ini dalam sistem koordinat belah ketupat dengan asal di sel pusat belah ketupat.

Grid pusat-pusat belah ketupat juga dibangun melalui sel-sel pusat belah ketupat, simpul-simpulnya terletak di dalam sel di persimpangan diagonal panjang dan pendek dengan angka yang merupakan kelipatan dari angka 5.
Dari gambar dengan rhombus jelas jenis grid apa yang terlibat. Untuk menggambarkan fitur rhombus, gambar sepasang rhombus di setiap setengah-pesawat diberikan. Rhombus ini ditandai dengan mengidentifikasi jumlah sel di bagian bawah dan sepasang rhombus semacam itu di setengah bidang atas. Penandaan belah ketupat di setengah-bidang di bawah D ₀ diagonal berbeda dari penandaan belah ketupat di setengah-pesawat di atasnya, tetapi dalam setengah-bidang yang sama, penandaan semua belah ketupat identik untuk kedua bidang bawah dan atas. Inti dari penandaan adalah pelokalan sel dengan angka yang memiliki infleksi yang sama (ditandai dengan mengisi sel dengan warna yang sama), mengatur koordinatnya x ₁ , x ₀ . Rhombus yang ditunjuk akan disebut fundamental, Rhombus lain dengan zoom in dapat dibentuk dari mereka.

Pusat-pusat belah ketupat dari setengah-bidang bawah adalah sel-sel dengan angka yang berakhir dengan dua digit baik 25 dengan angka horizontal dengan fleksi 5 dan dengan angka vertikal dengan fleksi 0, atau 75 dengan angka horizontal dengan fleksi 0 dan dengan angka vertikal dengan fleksi 5. Pada setengah bidang atas à ^{2 +} - submodel, semua angka dalam sel pusat dari semua belah ketupat diakhiri dengan dua digit 25. Selanjutnya, kami membatasi pertimbangan kami pada setengah bidang à ^{2 -} .


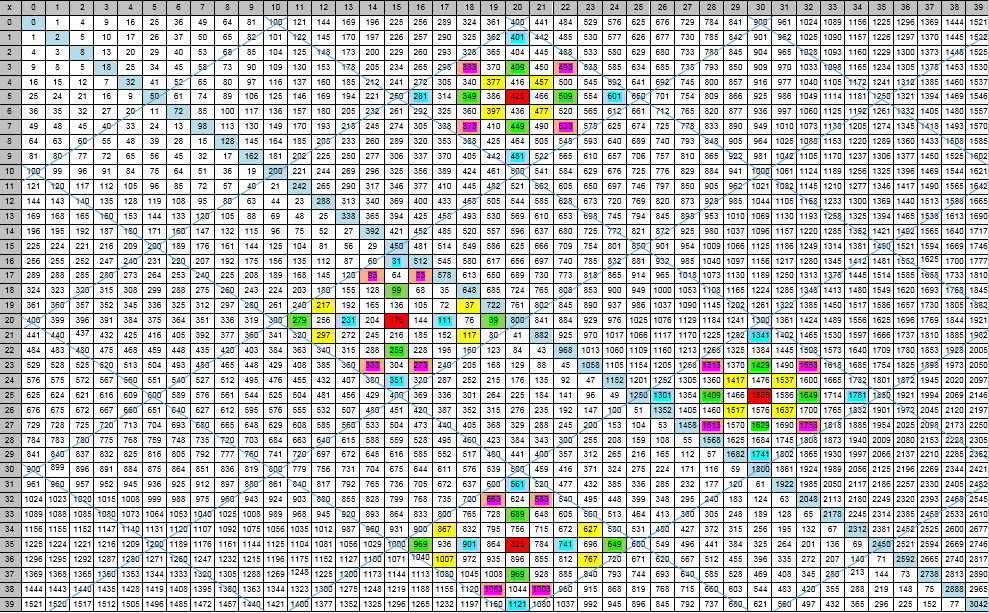_{Gambar 1— Representasi visual dari model berlian}

Definisi 1. Belah ketupat dasar adalah struktur à ^{2 ±} - model, dibatasi oleh dua diagonal pendek dan dua panjang dari bidang ini dengan angka yang merupakan kelipatan dari angka 10. Elemen utama yang mencirikan belah ketupat adalah sel ( x _1c , x _0c ) dari pusatnya. Pusat berisi nilai numerik N, kelipatan 5.

Definisi 2. Himpunan pusat rhombus fundamental adalah simpul (sel) dari jaringan pusat rhombus (SCR) dari memotong diagonal pendek dan panjang dengan angka yang merupakan kelipatan dari 5. Rhombus itu sendiri sepenuhnya menutupi bidang à ^{2 ±} - model (prinsip parket).

Semua belah ketupat diatur dengan cara yang sama, dan angka dalam sel mereka dengan ujung yang tetap ditempatkan pada posisi tetap (sel). Ini memungkinkan Anda untuk dengan mudah memfaktorkan angka ini ketika memecahkan masalah pelokalan nomor N dalam belah ketupat tertentu. Sepuluh horizontal yang sel-selnya membentuk belah ketupat dan belah ketupat (dengan koordinat yang berbeda dari itu) akan disebut keping belah ketupat. Pita horizontal dipertimbangkan: Barat-Timur (); vertikal: Utara-Selatan (NW), sepanjang diagonal pendek: Timur Laut (NE) dan sepanjang diagonal panjang: Utara-Barat (NW). Offset dari satu belah ketupat ke yang lain dapat dilengkapi dengan indikasi (atas dan ke bawah) di sepanjang pita yang ditunjukkan, di samping menunjukkan strip.

Karena mengikuti dari Definisi 2 bahwa set sel dari semua belah ketupat adalah semua sel dari model G2 ^± , maka di salah satu sel (x _1p , x _0p ) milik belah ketupat tertentu, bilangan komposit ganjil alami yang diberikan (ELF) N ( x _1p , x _0p ) = N (x ₁ , x ₀ ) . Pada saat yang sama, kami percaya bahwa adalah mungkin untuk menunjukkan belah ketupat seperti itu (dengan menentukan koordinat sel pusatnya) (x _1c , x _0c ) daripada menyelidiki semua sel, bahkan membatasi diri untuk memeriksa hanya diagonal ganjil.

Indikasi seperti belah ketupat dan sel yang diinginkan di dalamnya adalah solusi untuk masalah lokalisasi untuk nomor N tertentu (x ₁ , x ₀ ) . Masalah ini dan solusinya mendahului penerimaan keputusan WFCH. Arti dan tujuan akhir dari masalah lokalisasi adalah untuk menunjukkan dalam belah ketupat tertentu untuk ELF N yang diberikan (x ₁ , x ₀ ) nilai - nilai koordinat sel (x _1p , x _0p ) dalam model G ^{2 ±} , di mana ada angka yang bertepatan dengan N (x ₁ , x ₀ ) .

Dalam artikel ini, kami menggunakan mekanisme untuk menetapkan kepemilikan nomor N yang diberikan untuk belah ketupat tertentu dan sel di dalamnya. Mekanisme ini jauh dari yang terbaik, tetapi dalam contoh yang diusulkan itu mengatasi tugas. Pembaca diundang untuk menawarkan yang asli, atau memperbaiki mekanisme ini.

Mekanisme kami didasarkan pada keteraturan luar biasa dari model ^{G2 ±} yang ditemukan oleh penulis: keberadaan di garis horizontal dengan angka yang merupakan kelipatan lima (dan beberapa yang lain), sel dengan kuadrat elemen-elemen dari tripel Pythagoras (PFT) < g, k ₁ , k ₂ > = <hypotenuse , leg ₁ , leg ₂ >. CFT akan dibahas dalam karya lain.

Untuk menyederhanakan kesimpulan dan perhitungan, kita membutuhkan tiga sistem koordinat: planar, yang telah diperkenalkan , jaringan dengan sejumlah diagonal lainnya untuk SCR (Gambar 2) dan belah ketupat (Tabel 1), di mana permulaan dikaitkan dengan sel pusat belah ketupat.


<sub>Gambar 2. Penomoran (ganda) diagonal pendek dan
distribusi pusat berlian pada diagonal pendek

Tabel 1. Menentukan koordinat titik pencarian di dalam belah ketupat tetap</sub>



Dalam sistem SCR, berikut ini ditunjukkan: jumlah n diagonal pendek, c adalah nomor seri pusat di atasnya, serta nomor pusat C lebar jaringan, penomoran mereka sendiri diagonal pendek mulai dari n _p = 1 (dalam sistem planar adalah diagonal pendek ke-5) , maka angka n _p = 2 (ini adalah angka yang meningkat sebesar 10, yaitu bidang ke 15 K _i ) dan kemudian dengan langkah 10 yang lainnya. Posisi semua sel pusat belah ketupat di setiap K _i SCR juga dinomori dari c = 1 hingga c = 2n _{p dari} nomor jaringan ganda diagonal pendek.

Contoh 1 Biarkan diperlukan untuk menemukan nomor jaringan C dari pusat salah satu dari belah ketupat dan nomor N dalam sel ini untuk diagonal pendek yang diberikan melalui pusat-pusat rhombus, nomor jaringannya n _p = 5 , dan nomor seri pusat c = 3 dari salah satu dari belah ketupat di atasnya. Sederhananya, koordinat jaringan sel pusat dari belah ketupat ini direpresentasikan dalam bentuk ( _np , q) = (5, 3) .

1. Temukan bidang x ₁ koordinat sel pada awal diagonal yang diberikan (nd):
   x ₁ = x _nd = 10n _p - 5 = 50 - 5 = 45.
   Untuk kasus kami, kami mendapat x ₁ = x _nd = 45 .
   
2. Sekarang kita dapat segera melanjutkan untuk mencari koordinat bidang sel ( x _1c , x _sc ) dari pusat yang diinginkan: x ₁ = x _nd - 5 (c - 1) = 45 - 5 (3 - 1) = 35, x ₀ = 0 + 5 ( μ - 1) = 2 ∙ 5 = 10.
   
3. Temukan nomor jaringan dari pusat belah ketupat ( C ).
   
   Komentar. Diketahui bahwa untuk bilangan x rumus 2C _{x + 1} ² = x (x + 1) adalah jumlah kombinasi dua kali lipat dari x + 1 menjadi dua.
   Jumlah pusat sebelum diagonal pendek _np = 5 adalah 2n _p (n _p - 1) . Kemudian nomor seri C dari pusat jaringan diberikan oleh rumus
   C = n _p (n _p -1) + c = 2C _{n p} ² + 3 = 5 ∙ 4 + 3 = 23 .
   
4. Temukan nilai angka N (x _1c , x _sc ) di sel tengah belah ketupat N = x ₁ ² - x ₀ ² - tanda dalam rumus diambil tergantung pada posisi tengah relatif terhadap diagonal utama.
   N = 35 ² - 10 ² = 1125 - untuk kasus kami.
   

Jadi, dengan hanya memiliki nomor jaringan _{np dari} diagonal pendek yang melewati sel-sel pusat dan nomor pusat saat ini dari belah ketupat c pada diagonal ini, kita dapat memperoleh semua informasi lain tentang pusat belah ketupat.

Semua bilangan bulat positif aneh yang menarik dimiliki oleh sel intan. Konsep fleksi, digit terakhir dari angka, memungkinkan untuk melokalisasi posisi mereka di dalam belah ketupat. Untuk faktorisasi, angka-angka N yang diakhiri dengan angka 1, 3, 7, 9 menarik.

Bahkan bilangan tidak dianggap sebagai N , karena mereka memiliki pembagi utama 2. Bilangan yang berakhir dengan lima memiliki pembagi utama 5, yang juga tidak dapat diterima untuk N. Dianjurkan untuk melokalisasi N tertentu dengan infleksi dalam belah ketupat relatif ke pusat belah ketupat, dalam konteks fakta bahwa pusat adalah karakteristik paling penting dari belah ketupat. Berdasarkan fakta bahwa semua belah ketupat memiliki struktur yang sama, ada hubungan yang jelas antara jumlah N yang ditentukan untuk faktorisasi dan angka dalam sel belah ketupat dengan infleksi tertentu dan dalam sel pusat belah ketupat. Data tentang nomor-nomor hubungan tersebut diberikan dalam tabel. 1.

Namun, memilah semua belah ketupat di pesawat untuk menemukan belah ketupat yang diinginkan tidak dapat diterima baik dalam waktu maupun biaya komputasi. Dengan demikian, muncul masalah pelokalan daerah à ^{2 -} - submodels (setengah-pesawat), termasuk belah ketupat yang akan berisi angka awal N , untuk difaktorkan.

Tiga kali lipat Pythagoras . Untuk memecahkan masalah yang dirumuskan digunakan
Tiga kali lipat Pythagoras adalah tiga kali lipat angka yang memenuhi teorema Pythagoras: Yaitu, tiga kali lipat Pythagoras yang memenuhi aturan yang disebut segitiga Mesir, yaitu segitiga dengan sisi yang merupakan kelipatan 3, 4, 5.
Di setiap horisontal x _{1 yang} berisi pusat-pusat rhombus, ada satu atau lebih tiga kali lipat Pythagoras tersebut.

Belah ketupat pertama dalam masalah lokalisasi diindikasikan kira-kira dan dalam kasus "kehilangan", rhombus berikut harus dipilih. Untuk ini, perlu untuk menentukan arah pergerakan sepanjang SCR, sehingga secara bertahap mendekati tujuan akhir. Misalnya, jika yang lebih kecil dari 4 dalam belah ketupat angka saat ini lebih kecil dari N yang diberikan, maka belah ketupat Timur-Timur dan Timur mengandung bahkan kurang dari 4 angka, yaitu, belah ketupat seperti itu seharusnya tidak diselidiki. Pindah ke belah ketupat Barat menyebabkan peningkatan nilai di semua 4 selnya sehingga jumlah yang lebih kecil dari belah ketupat Barat ternyata lebih besar daripada jumlah yang lebih besar dari belah ketupat sebelumnya dan, oleh karena itu, lebih dari N. Oleh karena itu solusinya: bergerak naik dari belah ketupat ke belah ketupat ke arah barat laut.

Jika belah ketupat yang mengandung sel dengan angka sama dengan N (x _1p , x _0p ) = N ditemukan dan koordinat sel (x _1p , x _0p ) ditentukan, maka solusi FBCH ditentukan oleh hubungan dasar à ^{2 ±} - dari model
N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q

Subproblem lain adalah pemilihan dan implementasi urutan bypass sel dari belah ketupat yang dipilih untuk diselidiki. Di sini, urutan traversal berlawanan arah jarum jam diadopsi, mulai dari sel kiri atas yang berisi nomor dengan infleksi yang diperlukan. Dalam situasi kebetulan dari nilai-nilai dalam sel intan N (x _1p , x _0p ) dan angka yang diberikan N (x ₁ , x ₀ ), perbedaan di antara mereka ternyata menjadi nol.

Algoritma solusi ZFBCH menggunakan rhombus fundamental dan PFT

1. Kami mengekstrak root dari angka N. Membulatkan ke bawah.
   
2. Kami memeriksa apakah √N dapat dibagi dengan 3. Jika dapat dibagi, maka tetapkan nilai ini ke leg pertama k1, jika tidak, untuk memenuhi properti terbagi oleh 3, kurangi 1 atau 2 dari hasilnya, dan masukkan ke dalam memori sebagai k1. Hasil dari membagi nilai yang sepenuhnya dipilih oleh tiga M = √N / 3 - ingat koefisien PFT scaling.
   
3. Kami mendapatkan nilai untuk leg kedua k ₂ , menurut aturan segitiga Mesir, k ₂ = 4 ∙ M.
   
4. Kami menemukan nilai hypotenuse g = 5 ∙ M , dan nilai x ₁ = g harus dibagi dengan angka lima. Seperti yang Anda lihat, nilai sisi miring selalu sama dengan angka horisontal dengan PFT.
   
5. Temukan koordinat x ₁ = g .
   
6. Setelah itu, kami menentukan infleksi (digit terakhir) dari angka N , φ = N (mod10) .
   
7. Kami menemukan pusat belah ketupat yang paling dekat dengan k1 dan kemudian memeriksa belah ketupat yang berdekatan di salah satu jalur belah ketupat (ada 4 arah) untuk menemukan solusi.
   
8. Bergantung pada jenis infleksi yang kita dapatkan pada paragraf 6, kami menggunakan kolom (topeng) yang diinginkan dari yang disajikan dalam tabel. 1 untuk menentukan koordinat titik pencarian ( x _1p , x _0p ) dan menemukan nilai angka dalam sel ini _Np . Di setiap belah ketupat, hanya 4 sel yang diperiksa dari sel ke-41.
   
9. Setelah menetapkan bahwa angka N milik belah ketupat tertentu dan sel di dalamnya, berdasarkan tabel yang sama. 1 kita mendapatkan koordinat pesawat N: (x _1p , x _0p ) .
   
10. Menggunakan properti dari model matematika yang dipilih
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q
    kami mendapatkan representasi multiplikasi dari N dari aditif.
    
11. Jadi, pada output algoritma, kita memiliki: N = p ∙ q . Tergantung pada nilai fleksi f sesuai dengan rumus dalam tabel. 1, koordinat titik (x _1p , x _0p ) _ditentukan dan perbedaan ∆ = N (x _1p , x _0p ) - N (x ₁ , x ₀ ) dihitung. Jika ∆ ≠ 0 , maka pergi ke sel lain, jika semua sel belah ketupat diperiksa, kemudian ke belah ketupat lain.
    Jika Δ = 0 , maka x ₁ = x _1p , x ₀ = x _0p dan p = (x ₁ - x ₀ ) , q = N / p = (x ₁ + x ₀ ) .
    

Contoh 2. Diberikan: N = 1037 , angka dengan kapasitas 4. Diperlukan untuk memfaktorkannya. Kami bertindak sesuai dengan algoritma yang diberikan.

1. Kami mengekstrak root dari N : √N = 32.202 . Kami bulatkan: √N = 32 .
2. Kami memeriksa apakah 32 habis dibagi 3. Karena 32 tidak habis dibagi 3, kami kurangi 2. Jadi, kami berasumsi bahwa leg pertama adalah k ₁ = 3 ∙ 10 = 30 , di sini M = 10 = 30/3 adalah faktor penskalaan PFT .
3. Kami mendapatkan nilai untuk leg kedua k ₂ = 4 ∙ 10 = 40 .
4. Kami menemukan nilai hipotenuse g = (k ² ₁ + k ² ₂ ) ^0,5 , asalkan dibagi menjadi 5, (30 ² +40 ² ) ^0,5 = 50.
5. Jadi, x1 = k1 = 50 dan PFT berubah menjadi bentuk g = 50 , k ₁ = 30, k ₂ = 40 .
6. Kami menemukan belok dari angka N : φ (1037) = 1037 (mod10) = 7 .
7. Kami menemukan pusat belah ketupat paling dekat dengan N = 1037 .
   Ini akan memiliki koordinat sel pusat belah ketupat: x ₁ = 50, x ₀ = 35 . Koordinat pertama adalah nomor baris yang berisi CFT. Kuadrat dari kaki yang lebih kecil adalah 900, itu terkandung dalam vertikal dengan angka 40. Sel dengan angka 957 berakhir dengan tujuh yang paling dekat dengan 900 terletak pada horizontal sebelumnya dengan angka 49 dan di vertikal dengan angka 38. Ini adalah jumlah terkecil dari 4 dalam belah ketupat dan dengan infleksi 7. Di sini kita menggunakan data tabel 1. Pusat belah ketupat terdekat harus tiga sel ke kiri, yaitu, itu milik vertikal 38 - 3 = 35, ini adalah koordinat kedua dari pusat belah ketupat. Nilai angka dalam sel pusat belah ketupat adalah N (50, 35) = 1275
   
   Ini adalah belah ketupat dengan kuadrat kaki k ₁ dan k ₂ di perbatasannya. Di dalam belah ketupat ini, min adalah angka yang berakhir dengan tujuh 957 dalam sel ( x ₁ = 49, x ₀ = 38 ), dan angka lain dalam vertikal ini berakhir di 7 1157 , angka besar 1377 dan 1577 terletak di sebelah kiri sel pusat, bertepatan dengan angka N = 1037 no, oleh karena itu, perlu untuk naik ke belah ketupat ke kiri dan lebih tinggi dengan nilai di sel pusat 1125 dan dengan koordinat sel pusat ( x ₁ = 50 - 5 = 45, x ₀ = 35 - 5 = 30 ) Periksa empat angka untuk fleksi 7 Ini adalah 847, 1027, 1207 dan 1387 dan tidak ada kebetulan dengan N = 1037 dalam belah ketupat ini), kita akan naik lebih tinggi ke arah yang sama di sepanjang pita belah ketupat NW. Sel tengah belah ketupat baru memiliki nilai 975 dan koordinat ( x ₁ = 45 -5 = 40, x ₀ = 35 - 5 = 25 ). Kami memeriksa di dalam belah ketupat ini empat angka untuk infleksi 7. Ini adalah 737, 897, 1197 dan akhirnya kami mendapatkan 1037 di sel ( x _1p = 39, x _0p = 22 ), kami mendapat kecocokan lengkap dengan N. yang diberikan
   
   Secara rinci, tindakan ini diwakili oleh perhitungan berikut: Sesuai dengan Tabel 1, kami menghitung koordinat sel dan nilai angka di dalamnya. Setelah itu, kami menemukan perbedaan antara nilai N. yang dihitung dan diberikan. Dalam belah ketupat pertama, keempat sel dihitung.
   
   ∆ = N (x _1c -1, x _0c -3) - N (x ₁ , x ₀ ) = N (49,32) - 1037 = 1377 - 1037 = 340 ≠ 0,
   ∆ = N (x _1c +1, x _0c -3) - N (x ₁ , x ₀ ) = N (51,32) - 1037 = 1577 - 1037 = 540 ≠ 0,
   ∆ = N (x _1c +1, x _0c +3) - N (x ₁ , x ₀ ) = N (51,38) - 1037 = 1157 - 1037 = 120 ≠ 0,
   ∆ = N (x _1c -1, x _0c +3) - N (x ₁ , x ₀ ) = N (49,38) - 1037 = 957 - 1037 = - 80 ≠ 0.
   Dalam belah ketupat ini tidak ada kebetulan dari angka N dengan jumlah di dalam sel.
   
   Kita pergi ke belah ketupat berikutnya dengan pusat di sel (x _1c -5, x _0c -5) = (45, 30) dan nilai di dalamnya N (x _1c -5, x _0c -5) = N (45, 30) = 1125 .
   ∆ = N (x _1ts -1, x _0ts -3) - N (x ₁ , x ₀ ) = N (44.27) - 1037 = 1207 - 1037 = 170 ≠ 0,
   ∆ = N (x _1c +1, x _0c -3) - N (x ₁ , x ₀ ) = N (46.27) - 1037 = 1387 - 1037 = 350 ≠ 0,
   ∆ = N (x _1c +1, x _0c +3) - N (x ₁ , x ₀ ) = N (46,33) - 1037 = 1027 - 1037 = - 10 ≠ 0,
   ∆ = N (x _1c -1, x _0c +3) - N (x ₁ , x ₀ ) = N (44,33) - 1037 = 847 - 1037 = - 190 ≠ 0.
   Dalam belah ketupat ini, tidak ada kebetulan dari angka N dengan angka di dalam sel juga.
   
   Kita pergi ke belah ketupat berikutnya dengan pusat di sel (x _1c -5, x _0c -5) = (40, 25) dan nilai di dalamnya N (x _1c -5, x _0c -5) = N (40, 25) = 975
   ∆ = N (x _1c -1, x _0c -3) - N (x ₁ , x ₀ ) = N (39.22) - 1037 = 1037 - 1037 = 0.
   Mendapat nol perbedaan nilai. Ada suatu kebetulan yang lengkap. Dari sini dapat disimpulkan bahwa angka yang diberikan N (x ₁ , x ₀ ) = 1037 terkandung dalam sel dengan koordinat (x 1 _r , x 0 _r ) = (39, 22). Akhirnya, solusi HFBC ditentukan oleh hubungan dasar à ^{2 ±} - dari model
   N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = (39 - 22) (39 + 22) = p ∙ q = 17 ∙ 61 .
   
8. Anda dapat bertindak berbeda, dimulai dengan belah ketupat yang ditunjukkan pada paragraf 6, menggunakan tabel. 1, kita mencari tahu apakah nomor N milik belah ketupat tertentu, bergerak di antara pusat-pusat belah ketupat pertama secara horizontal, menuju diagonal utama, kemudian bergerak ke bawah ke potongan berikutnya dari belah ketupat dan mengulangi semuanya lagi.
9. Setelah menetapkan bahwa angka N milik belah ketupat tertentu (dalam kasus kami, belah ketupat akan memiliki koordinat ( x ₁ = 40, x ₀ = 25 )) berdasarkan tabel yang sama. 1 kita mendapatkan koordinat N : x _1p = 39 , x _2p = 22 (9 belah ketupat dilihat).
10. Menggunakan properti dari model matematika nomor yang dipilih
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q
    kami mendapatkan representasi multiplikasi N dari aditif:
    N = (39 - 22) (39 + 22) = 17 ∙ 61 = 1037 .

Dengan demikian, pada output kita memiliki N = p · q = 17 · 61 = 1037 , yaitu, solusi untuk masalah diperoleh dengan sukses.

Kami juga mendapatkan hasil dari solusi perangkat lunak untuk masalah dalam contoh 3.

Contoh 3 Diberikan: N = 3808572773, angka dengan resolusi 10.

1. Kami mengekstrak root dari N: √N = 61713 , 64 = 61713 .
2. Periksa apakah 61713 dapat dibagi 3. Karena 61713 dapat dibagi 3,
   6 + 1 + 7 + 1 + 3 = 18 dibagi 3, maka leg pertama k ₁ sama dengan k ₁ = 61713 .
3. Kita mendapatkan leg kedua k ₂ = 4k 1/3 => 4k 2/3 = 82284 .
4. Kami menemukan hypotenuse g = √k ₁₂ + k ₂₂ , asalkan dibagi
   5 g = √617132 + 822842 = 102855 .
5. Jadi, x ₁ = k ₁ = 61713 , dan triple Pythagoras bertransformasi masing-masing ke bentuk k ₁ = 61713, k ₂ = 82284, g = 102855 .
6. N: (3808572773) = 3808572773(mod10) = 3 .
7. . x ₁ = 61715; x ₉ = 0 .
8. , 7, . 1, N , , , , .
9. N ( x ₁ = 62015 , x ₀ = 6085 ) N :
   x _1p = 62013; x _0p = 6086 ; ( 60 ).
10. 
    N = x ² ₁ — x ² ₀ = (x ₁ — x ₀ )(x ₁ + x ₀ ) =p ·q N :
    N = (62013 — 6086) · (62013 + 62086) = 55927 · 68099 = 3808572773 ;
11. , N = p · q = 55927 · 68099 = 3808572773 , . . .