Bayangkan Anda perlu membuat angka acak yang terdistribusi secara merata dari 1 hingga 10. Yaitu, bilangan bulat dari 1 hingga 10 inklusif, dengan probabilitas yang sama (10%) dari setiap kejadian. Tetapi, katakanlah, tanpa akses ke koin, komputer, bahan radioaktif, atau sumber serupa lainnya dari nomor semu. Anda hanya punya kamar dengan orang.

Misalkan ada sedikit lebih dari 8500 siswa di ruangan ini.

Yang paling sederhana adalah bertanya kepada seseorang: "Hei, pilih nomor acak dari satu hingga sepuluh!". Pria itu menjawab: "Tujuh!". Hebat! Sekarang kamu punya nomor. Namun, Anda mulai bertanya-tanya apakah itu didistribusikan secara merata.

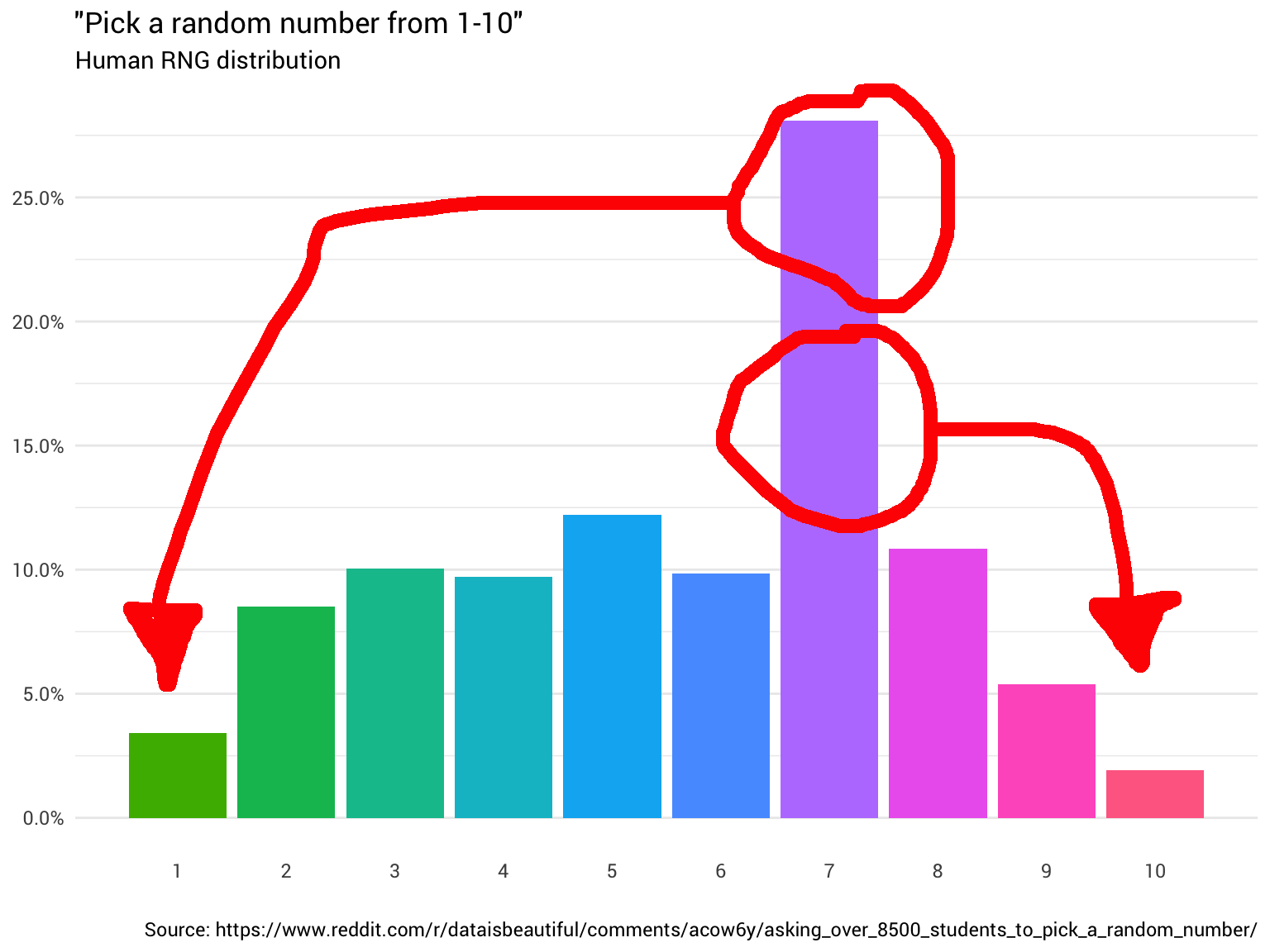
Jadi Anda memutuskan untuk bertanya kepada beberapa orang lagi. Anda terus bertanya kepada mereka dan menghitung jawaban mereka, membulatkan bilangan pecahan dan mengabaikan mereka yang berpikir bahwa kisaran dari 1 hingga 10 mencakup 0. Pada akhirnya, Anda mulai melihat bahwa distribusi tidak sama sekali:

library(tidyverse) probabilities <- read_csv("https://git.io/fjoZ2") %>% count(outcome = round(pick_a_random_number_from_1_10)) %>% filter(!is.na(outcome), outcome != 0) %>% mutate(p = n / sum(n)) probabilities %>% ggplot(aes(x = outcome, y = p)) + geom_col(aes(fill = as.factor(outcome))) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = '"Pick a random number from 1-10"', subtitle = "Human RNG distribution", x = "", y = NULL, caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/") 

Data dari Reddit

Anda menampar dahi Anda. Yah, tentu saja , itu tidak akan acak. Bagaimanapun, Anda tidak bisa mempercayai orang .

Jadi apa yang harus dilakukan?

Saya berharap dapat menemukan beberapa fungsi yang mengubah distribusi "RNG manusia" menjadi distribusi yang seragam ...

Intuisi di sini relatif sederhana. Anda hanya perlu mengambil massa distribusi dari tempat di atas 10%, dan memindahkannya ke tempat di bawah 10%. Sehingga semua kolom pada bagan berada pada level yang sama:



Secara teori, fungsi seperti itu harus ada. Bahkan, harus ada banyak fungsi berbeda (untuk permutasi). Dalam kasus ekstrem, Anda dapat "memotong" setiap kolom menjadi balok-balok kecil tanpa batas dan membangun distribusi dalam bentuk apa pun (seperti batu bata Lego).

Tentu saja, contoh ekstrem semacam itu agak rumit. Idealnya, kami ingin mempertahankan sebanyak mungkin distribusi awal (mis., Untuk membuat serpihan dan gerakan sesedikit mungkin).

Bagaimana menemukan fungsi seperti itu?

Nah, penjelasan kami di atas sangat mirip dengan pemrograman linear . Dari Wikipedia:

Linear programming (LP, juga disebut optimasi linear) adalah metode untuk mencapai hasil terbaik ... dalam model matematika yang persyaratannya diwakili oleh hubungan linear ... Bentuk standar adalah bentuk yang biasa dan paling intuitif untuk menggambarkan masalah pemrograman linear. Ini terdiri dari tiga bagian:

• Fungsi linear menjadi maksimal
  
• Batasan masalah dari formulir berikut
  
• Variabel non-negatif

Demikian pula, masalah redistribusi dapat dirumuskan.

Presentasi masalah

Kami memiliki serangkaian variabel $$$(x_ {i, j}$ , masing-masing mengkodekan sebagian kecil dari probabilitas yang didistribusikan kembali dari integer $$$i$ (1 hingga 10) ke integer $$$j$ (dari 1 hingga 10). Karena itu, jika $$$(x_ {7,1} = 0,2$ , maka kita perlu mentransfer 20% jawaban dari tujuh menjadi satu.

 variables <- crossing(from = probabilities$outcome, to = probabilities$outcome) %>% mutate(name = glue::glue("x({from},{to})"), ix = row_number()) variables 

  ## # Camilan: 100 x 4
 ## dari ke nama ix
 ## <dbl> <dbl> <glue> <int>
 ## 1 1 1 x (1,1) 1
 ## 2 1 2 x (1,2) 2
 ## 3 1 3 x (1,3) 3
 ## 4 1 4 x (1,4) 4
 ## 5 1 5 x (1,5) 5
 ## 6 1 6 x (1,6) 6
 ## 7 1 7 x (1,7) 7
 ## 8 1 8 x (1,8) 8
 ## 9 1 9 x (1.9) 9
 ## 10 1 10 x (1,10) 10
 ## # ... dengan 90 baris lagi 

Kami ingin membatasi variabel-variabel ini sehingga semua probabilitas yang didistribusikan kembali bertambah hingga 10%. Dengan kata lain, untuk masing-masing $$$j$ dari 1 hingga 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0,1$$

Kita dapat mewakili batasan ini sebagai daftar array di R. Kemudian, kita mengikatnya ke dalam matriks.

 fill_array <- function(indices, weights, dimensions = c(1, max(variables$ix))) { init <- array(0, dim = dimensions) if (length(weights) == 1) { weights <- rep_len(1, length(indices)) } reduce2(indices, weights, function(a, i, v) { a[1, i] <- v a }, .init = init) } constrain_uniform_output <- probabilities %>% pmap(function(outcome, p, ...) { x <- variables %>% filter(to == outcome) %>% left_join(probabilities, by = c("from" = "outcome")) fill_array(x$ix, x$p) }) 

Kita juga harus memastikan bahwa seluruh massa probabilitas dari distribusi awal dipertahankan. Jadi untuk semuanya $$$j$ dalam kisaran 1 hingga 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0,1$$

 one_hot <- partial(fill_array, weights = 1) constrain_original_conserved <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome) %>% pull(ix) %>% one_hot() }) 

Seperti yang telah disebutkan, kami ingin memaksimalkan kelestarian distribusi asli. Ini adalah tujuan kami:

$$

$$maksimalkan (x_ {1, 1} + x_ {2, 2} + \ ldots \ x_ {10, 10})$$

 maximise_original_distribution_reuse <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome, to == outcome) %>% pull(ix) %>% one_hot() }) objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums() 

Lalu kami meneruskan masalah ke solver, misalnya, paket lpSolve di R, menggabungkan batasan yang dibuat menjadi satu matriks:

 # Make results reproducible... set.seed(23756434) solved <- lpSolve::lp( direction = "max", objective.in = objective, const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)), const.dir = c(rep_len("==", length(constrain_original_conserved)), rep_len("==", length(constrain_uniform_output))), const.rhs = c(rep_len(1, length(constrain_original_conserved)), rep_len(1 / nrow(probabilities), length(constrain_uniform_output))) ) balanced_probabilities <- variables %>% mutate(p = solved$solution) %>% left_join(probabilities, by = c("from" = "outcome"), suffix = c("_redistributed", "_original")) 

Redistribusi berikut dikembalikan:

 library(gganimate) redistribute_anim <- bind_rows(balanced_probabilities %>% mutate(key = from, state = "Before"), balanced_probabilities %>% mutate(key = to, state = "After")) %>% ggplot(aes(x = key, y = p_redistributed * p_original)) + geom_col(aes(fill = as.factor(from)), position = position_stack()) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = 'Balancing the "Human RNG distribution"', subtitle = "{closest_state}", x = "", y = NULL) + transition_states( state, transition_length = 4, state_length = 3 ) + ease_aes('cubic-in-out') animate( redistribute_anim, start_pause = 8, end_pause = 8 ) 

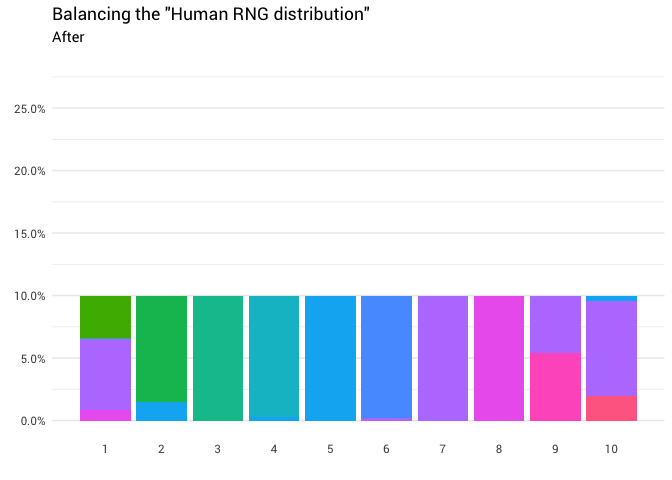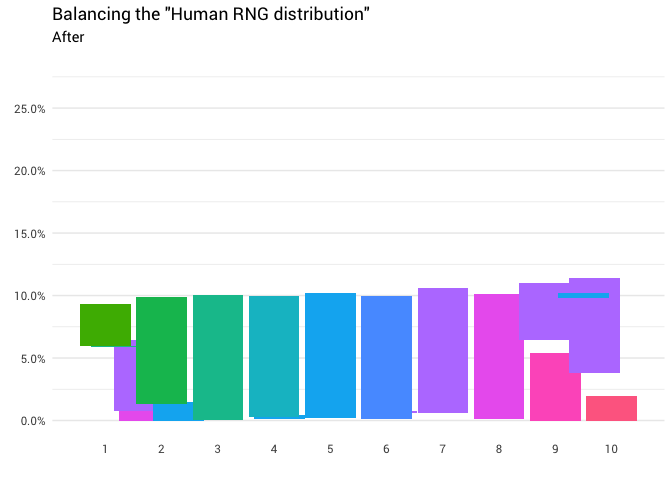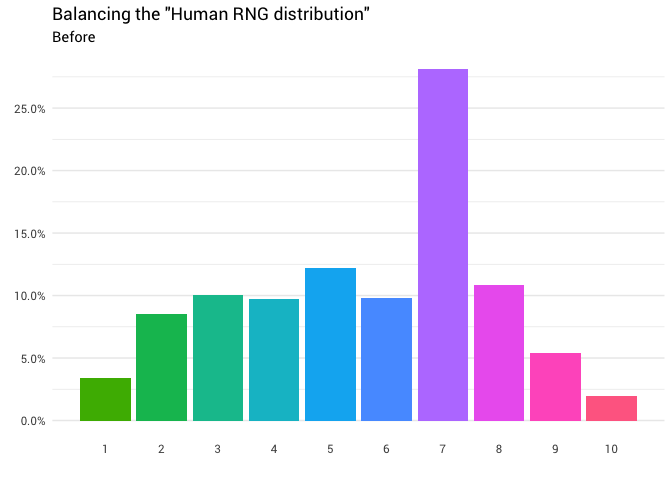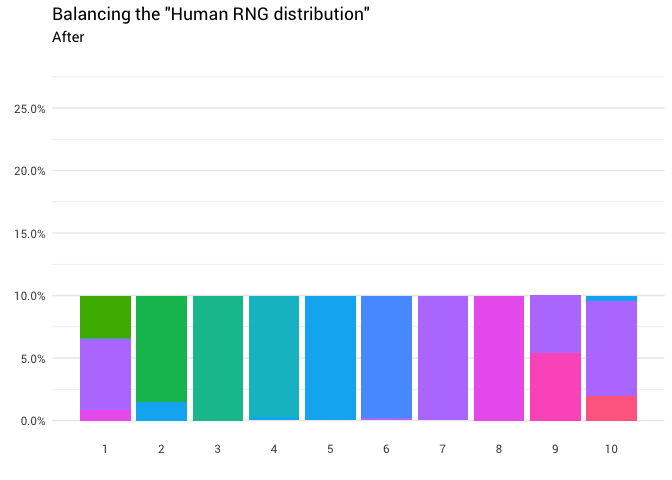
Hebat! Sekarang kami memiliki fungsi redistribusi. Mari kita lihat lebih dekat bagaimana massa bergerak:

 balanced_probabilities %>% ggplot(aes(x = from, y = to)) + geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) + geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) + scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) + scale_fill_discrete(h = c(120, 360)) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(breaks = 1:10) + theme_minimal(base_family = "Roboto") + theme(panel.grid.minor = element_blank(), panel.grid.major = element_line(linetype = "dotted"), legend.position = "none") + labs(title = "Probability mass redistribution", x = "Original number", y = "Redistributed number") 

Bagan ini mengatakan bahwa dalam sekitar 8% kasus ketika seseorang memanggil delapan sebagai angka acak, Anda perlu mengambil jawabannya sebagai satu kesatuan. Dalam sisa 92% kasus, ia tetap delapan.

Akan sangat sederhana untuk menyelesaikan masalah jika kita memiliki akses ke generator nomor acak yang terdistribusi secara merata (dari 0 hingga 1). Tapi kami hanya punya kamar yang penuh dengan orang. Untungnya, jika Anda siap untuk berdamai dengan beberapa ketidakakuratan kecil, maka Anda dapat membuat RNG yang cukup baik dari orang-orang tanpa bertanya lebih dari dua kali.

Kembali ke distribusi asli kami, kami memiliki probabilitas berikut untuk setiap nomor, yang dapat digunakan untuk menetapkan kembali probabilitas apa pun, jika perlu.

 probabilities %>% transmute(number = outcome, probability = scales::percent(p)) 

  ## # Camilan: 10 x 2
 ## angka probabilitas
 ## <dbl> <chr>
 ## 1 1 3,4%
 ## 2 2 8.5%
 ## 3 3 10.0%
 ## 4 4 9.7%
 ## 5 5 12.2%
 ## 6 6 9,8%
 ## 7 7 28.1%
 ## 8 8 10.9%
 ## 9 9 5,4%
 ## 10 10 1.9% 

Misalnya, ketika seseorang memberi kita delapan sebagai angka acak, kita perlu menentukan apakah delapan ini harus menjadi satu unit atau tidak (probabilitas 8%). Jika kita bertanya kepada orang lain tentang angka acak, maka dengan probabilitas 8,5% dia akan menjawab "dua". Jadi, jika angka kedua ini 2, kita tahu bahwa kita harus mengembalikan 1 sebagai angka acak yang terdistribusi secara seragam .

Memperluas logika ini ke semua angka, kami mendapatkan algoritma berikut:

• Minta seseorang untuk nomor acak, $$$n_1$ .
• $$$n_1 = 1, 2, 3, 4, 6, 9,$ atau $$$10$ :
  
  • Nomor acak Anda $$$n_1$
• Jika $$$n_1 = 5$ :
  
  • Minta nomor acak kepada orang lain ( $$$n_2$ )
  • Jika $$$n_2 = 5$ (12,2%):
    
    • Nomor acak Anda 2
  • Jika $$$n_2 = 10$ (1,9%):
    
    • Nomor acak Anda 4
  • Jika tidak, nomor acak Anda adalah 5
• Jika $$$n_1 = 7$ :
  
  • Minta nomor acak kepada orang lain ( $$$n_2$ )
  • Jika $$$n_2 = 2$ atau $$$5$ (20,7%):
    
    • Nomor acak 1 Anda
  • Jika $$$n_2 = 8$ atau $$$9$ (16,2%):
    
    • Nomor acak Anda adalah 9
  • Jika $$$n_2 = 7$ (28,1%):
    
    • Nomor acak Anda adalah 10
  • Jika tidak, nomor acak Anda adalah 7
• Jika $$$n_1 = 8$ :
  
  • Minta nomor acak kepada orang lain ( $$$n_2$ )
  • Jika $$$n_2 = 2$ (8,5%):
    
    • Nomor acak 1 Anda
  • Jika tidak, nomor acak Anda adalah 8

Dengan menggunakan algoritma ini, Anda dapat menggunakan sekelompok orang untuk mendapatkan sesuatu yang dekat dengan generator nomor acak yang terdistribusi secara merata dari 1 hingga 10!