Jaringan saraf dan pembelajaran mendalam, bab 3, bagian 2: mengapa regularisasi membantu mengurangi pelatihan ulang?

Secara empiris, kita telah melihat bahwa regularisasi membantu mengurangi pelatihan ulang. Ini menginspirasi - tetapi, sayangnya, tidak jelas mengapa regularisasi membantu. Biasanya orang menjelaskannya dengan cara tertentu: dalam arti, bobot yang lebih kecil memiliki kompleksitas yang lebih sedikit, yang memberikan penjelasan data yang lebih sederhana dan lebih efisien, sehingga mereka harus lebih disukai. Namun, ini penjelasan yang terlalu singkat, dan beberapa bagiannya mungkin tampak meragukan atau misterius. Mari kita buka kisah ini dan memeriksanya dengan mata kritis. Untuk melakukan ini, misalkan kita memiliki kumpulan data sederhana yang ingin kita buat model:


Dalam hal makna, di sini kita mempelajari fenomena dunia nyata, dan x dan y menunjukkan data nyata. Tujuan kami adalah untuk membangun model yang memungkinkan kami untuk memprediksi y sebagai fungsi x. Kita dapat mencoba menggunakan jaringan saraf untuk membuat model seperti itu, tetapi saya menyarankan sesuatu yang lebih sederhana: Saya akan mencoba memodelkan y sebagai polinomial dalam x. Saya akan melakukan ini alih-alih jaringan saraf, karena penggunaan polinomial membuat penjelasan lebih jelas. Segera setelah kami menangani kasus polinomial, kami akan beralih ke Majelis Nasional. Ada sepuluh poin pada grafik di atas, yang berarti bahwa kita dapat menemukan polinomial orde ke-9 y = a ₀ x ⁹ + a ₁ x ⁸ + ... + a ₉ yang persis sesuai dengan data. Dan ini adalah grafik polinomial ini.


Pukulan sempurna. Tapi kita bisa mendapatkan perkiraan yang baik menggunakan model linier y = 2x


Mana yang lebih baik? Mana yang lebih mungkin benar? Mana yang akan digeneralisasikan dengan lebih baik pada contoh-contoh lain dari fenomena yang sama dari dunia nyata?

Pertanyaan sulit. Dan mereka tidak dapat dijawab dengan tepat tanpa informasi tambahan tentang fenomena dunia nyata yang mendasarinya. Namun, mari kita lihat dua kemungkinan: (1) model dengan polinomial orde ke-9 benar-benar menggambarkan fenomena dunia nyata, dan karenanya, menggeneralisasi dengan sempurna; (2) model yang benar adalah y = 2x, tetapi kami memiliki noise tambahan yang terkait dengan kesalahan pengukuran, sehingga model tersebut tidak cocok dengan sempurna.

A priori, seseorang tidak bisa mengatakan mana dari dua kemungkinan yang benar (atau tidak ada yang ketiga). Logikanya, salah satu dari mereka mungkin ternyata benar. Dan perbedaan di antara mereka adalah nontrivial. Ya, berdasarkan data yang tersedia, dapat dikatakan bahwa hanya ada sedikit perbedaan antara model. Tapi anggaplah kita ingin memprediksi nilai y yang sesuai dengan beberapa nilai x yang besar, jauh lebih besar daripada yang ditunjukkan dalam grafik. Jika kita mencoba melakukan ini, maka perbedaan besar akan muncul antara prediksi kedua model, karena istilah x ⁹ mendominasi dalam polinomial orde ke-9, dan model linier tetap linier.

Satu sudut pandang tentang apa yang terjadi adalah untuk menyatakan bahwa penjelasan yang lebih sederhana harus digunakan dalam sains, jika memungkinkan. Ketika kami menemukan model sederhana yang menjelaskan banyak poin referensi, kami hanya ingin berteriak: "Eureka!" Lagi pula, kecil kemungkinan bahwa penjelasan sederhana akan muncul murni secara kebetulan. Kami menduga bahwa model tersebut harus menghasilkan beberapa kebenaran yang terkait dengan fenomena tersebut. Dalam hal ini, model y = 2x + noise tampaknya jauh lebih sederhana daripada y = a ₀ x ⁹ + a ₁ x ⁸ + ... Akan mengejutkan jika kesederhanaan muncul secara kebetulan, jadi kami menduga bahwa y = 2x + noise mengekspresikan beberapa kebenaran yang mendasarinya. Dari sudut pandang ini, model urutan ke-9 hanya mempelajari efek kebisingan lokal. Meskipun model urutan ke-9 bekerja dengan sempurna untuk titik-titik referensi khusus ini, ia tidak dapat menggeneralisasi ke titik-titik lain, sehingga model linier dengan noise akan memiliki kemampuan prediksi yang lebih baik.

Mari kita lihat apa arti sudut pandang ini untuk jaringan saraf. Misalkan, di jaringan kami, terutama ada bobot yang rendah, seperti yang biasanya terjadi pada jaringan yang diatur. Karena bobotnya yang kecil, perilaku jaringan tidak banyak berubah ketika beberapa input acak diubah di sana-sini. Akibatnya, jaringan yang teregulasi sulit untuk mempelajari efek noise lokal yang ada dalam data. Ini mirip dengan keinginan untuk memastikan bahwa bukti individual tidak sangat mempengaruhi hasil jaringan secara keseluruhan. Alih-alih, jaringan yang diatur dilatih untuk menanggapi bukti yang sering ditemukan dalam data pelatihan. Sebaliknya, jaringan dengan bobot besar dapat mengubah perilakunya dengan cukup kuat sebagai respons terhadap perubahan kecil pada data input. Oleh karena itu, jaringan tidak teratur dapat menggunakan bobot besar untuk melatih model yang kompleks yang berisi banyak informasi gangguan dalam data pelatihan. Singkatnya, keterbatasan jaringan yang diatur memungkinkan mereka untuk membuat model yang relatif sederhana berdasarkan pola yang sering ditemukan dalam data pelatihan, dan mereka tahan terhadap penyimpangan yang disebabkan oleh kebisingan dalam data pelatihan. Ada harapan bahwa ini akan membuat jaringan kita mempelajari fenomena itu sendiri, dan lebih menggeneralisasi pengetahuan yang didapat.

Dengan semua yang dikatakan, gagasan memberikan preferensi pada penjelasan yang lebih sederhana harus membuat Anda gugup. Kadang-kadang orang menyebut ide ini "Occam's razor" dan dengan bersemangat menerapkannya, seolah-olah memiliki status prinsip ilmiah umum. Tapi ini, tentu saja, bukan prinsip ilmiah umum. Tidak ada alasan logis apriori untuk lebih memilih penjelasan sederhana daripada yang kompleks. Terkadang penjelasan yang lebih rumit benar.

Izinkan saya menjelaskan dua contoh bagaimana penjelasan yang lebih rumit ternyata benar. Pada 1940-an, fisikawan Marcel Shane mengumumkan penemuan partikel baru. Perusahaan tempat dia bekerja, General Electric, senang, dan secara luas mendistribusikan publikasi acara ini. Namun, fisikawan Hans Bethe skeptis. Bethe mengunjungi Shane dan mempelajari lemping-lemping itu dengan jejak partikel baru Shane. Shane menunjukkan piring Beta setelah piring, tetapi Bete menemukan pada masing-masing dari mereka masalah yang menunjukkan perlunya menolak data ini. Akhirnya, Shane menunjukkan Beta sebuah catatan yang tampak pas. Bethe mengatakan itu mungkin hanya penyimpangan statistik. Shane: "Ya, tetapi kemungkinan itu karena statistik, bahkan dengan formula Anda sendiri, adalah satu dari lima." Bethe: "Namun, saya sudah melihat lima catatan." Akhirnya, Shane berkata, "Tetapi Anda menjelaskan masing-masing catatan saya, setiap citra yang baik dengan beberapa teori lain, dan saya memiliki satu hipotesis yang menjelaskan semua catatan sekaligus, dari mana selanjutnya kita berbicara tentang partikel baru." Bethe menjawab: “Satu-satunya perbedaan antara penjelasan saya dan Anda adalah bahwa Anda salah dan milik saya benar. Penjelasan tunggal Anda salah, dan semua penjelasan saya benar. " Selanjutnya, ternyata alam setuju dengan Bethe, dan partikel Shane menguap.

Dalam contoh kedua, pada 1859, astronom Urbain Jean Joseph Le Verrier menemukan bahwa bentuk orbit Merkurius tidak sesuai dengan teori gravitasi universal Newton. Ada sedikit penyimpangan dari teori ini, dan kemudian beberapa opsi untuk memecahkan masalah diusulkan, yang bermuara pada fakta bahwa teori Newton secara keseluruhan adalah benar, dan hanya memerlukan sedikit perubahan. Dan pada tahun 1916, Einstein menunjukkan bahwa penyimpangan ini dapat dijelaskan dengan baik menggunakan teori relativitas umumnya, secara radikal berbeda dari gravitasi Newton dan didasarkan pada matematika yang jauh lebih kompleks. Terlepas dari kompleksitas tambahan ini, secara umum diterima hari ini bahwa penjelasan Einstein benar, dan gravitasi Newton tidak benar bahkan dalam bentuk yang dimodifikasi . Ini terjadi, khususnya, karena hari ini kita tahu bahwa teori Einstein menjelaskan banyak fenomena lain yang dengannya teori Newton mengalami kesulitan. Selain itu, bahkan lebih menakjubkan, teori Einstein secara akurat memprediksi beberapa fenomena yang tidak diprediksi oleh gravitasi Newton. Namun, kualitas yang mengesankan ini tidak terlihat jelas di masa lalu. Menilai berdasarkan kesederhanaan belaka, maka beberapa bentuk modifikasi dari teori Newton akan terlihat lebih menarik.

Tiga moralitas dapat ditarik dari kisah-kisah ini. Pertama, kadang-kadang cukup sulit untuk memutuskan mana dari dua penjelasan yang akan "lebih mudah." Kedua, bahkan jika kita membuat keputusan seperti itu, kesederhanaan harus dibimbing dengan sangat hati-hati! Ketiga, tes sebenarnya dari model bukanlah kesederhanaan, tetapi seberapa baik ia memprediksi fenomena baru dalam kondisi perilaku yang baru.

Mempertimbangkan semua ini dan berhati-hati, kami akan menerima fakta empiris - NS yang diatur biasanya lebih digeneralisasikan daripada yang tidak teratur. Karena itu, nanti dalam buku kita akan sering menggunakan regularisasi. Cerita-cerita yang disebutkan di atas hanya diperlukan untuk menjelaskan mengapa belum ada yang mengembangkan penjelasan teoretis yang sepenuhnya meyakinkan tentang mengapa regularisasi membantu jaringan secara umum. Para peneliti terus menerbitkan karya-karya di mana mereka mencoba untuk mencoba pendekatan berbeda untuk regularisasi, membandingkannya, melihat mana yang terbaik, dan mencoba memahami mengapa pendekatan yang berbeda bekerja lebih buruk atau lebih baik. Jadi regularisasi dapat diperlakukan seperti awan . Saat ini cukup membantu, kami tidak memiliki pemahaman sistemik yang sepenuhnya memuaskan tentang apa yang terjadi - hanya aturan heuristik dan praktis yang tidak lengkap.

Di sinilah letak masalah yang lebih dalam yang masuk ke jantung ilmu pengetahuan. Ini adalah masalah generalisasi. Regularisasi dapat memberi kita tongkat ajaib komputasi yang membantu jaringan kita menggeneralisasikan data dengan lebih baik, tetapi itu tidak memberikan pemahaman dasar tentang bagaimana generalisasi bekerja, dan apa pendekatan terbaik untuk itu.

Masalah-masalah ini kembali ke masalah induksi , interpretasi terkenal yang dilakukan oleh filsuf Skotlandia David Hume dalam buku " A Study on Human Cognition " (1748). Masalah induksi adalah subjek dari " teorema tentang tidak adanya makanan gratis " oleh David Walpert dan William Macredie (1977).

Dan ini sangat menjengkelkan, karena dalam kehidupan sehari-hari orang secara fenomenal mampu menggeneralisasikan data. Perlihatkan beberapa gambar gajah kepada anak, dan ia akan segera belajar mengenali gajah lain. Tentu saja, ia kadang-kadang dapat membuat kesalahan, misalnya, membingungkan badak dengan gajah, tetapi secara umum, proses ini bekerja dengan sangat akurat. Sekarang, kami memiliki sistem - otak manusia - dengan sejumlah besar parameter gratis. Dan setelah dia diperlihatkan satu atau lebih gambar pelatihan, sistem belajar untuk menggeneralisasikannya ke gambar lain. Otak kita, dalam arti tertentu, sangat bagus dalam mengatur! Tetapi bagaimana kita melakukan ini? Saat ini, ini tidak kami ketahui. Saya pikir bahwa di masa depan kita akan mengembangkan teknologi regularisasi yang lebih kuat dalam jaringan saraf tiruan, teknik yang pada akhirnya memungkinkan Majelis Nasional untuk menggeneralisasikan data berdasarkan pada set data yang lebih kecil.

Bahkan, jaringan kami sudah menggeneralisasi jauh lebih baik daripada yang dapat diperkirakan secara apriori. Jaringan dengan 100 neuron tersembunyi memiliki hampir 80.000 parameter. Kami hanya memiliki 50.000 gambar dalam data pelatihan. Ini sama dengan mencoba meregangkan polinomial dengan urutan 80.000 lebih dari 50.000 poin referensi. Dengan semua indikasi, jaringan kami harus sangat berlatih. Namun, seperti yang telah kita lihat, jaringan seperti itu sebenarnya sebenarnya cukup baik untuk digeneralisasi. Mengapa ini terjadi? Ini tidak sepenuhnya jelas. Dihipotesiskan bahwa "dinamika pembelajaran dengan penurunan gradien dalam jaringan multilayer tunduk pada pengaturan diri." Ini adalah kekayaan yang ekstrem, tetapi juga fakta yang agak mengganggu, karena kita tidak mengerti mengapa ini terjadi. Sementara itu, kami akan mengambil pendekatan pragmatis, dan kami akan menggunakan regularisasi jika memungkinkan. Ini akan bermanfaat bagi Majelis Nasional kita.

Biarkan saya menyelesaikan bagian ini dengan kembali ke apa yang saya tidak jelaskan sebelumnya: bahwa regularisasi L2 tidak membatasi perpindahan. Tentu, akan mudah untuk mengubah prosedur regularisasi sehingga mengatur perpindahan. Tetapi secara empiris, ini seringkali tidak mengubah hasil dengan cara yang terlihat, oleh karena itu, sampai batas tertentu, untuk berurusan dengan regularisasi bias, atau tidak, adalah masalah kesepakatan. Namun, perlu dicatat bahwa perpindahan besar tidak membuat neuron sensitif terhadap input seperti bobot besar. Oleh karena itu, kita tidak perlu khawatir tentang offset besar yang memungkinkan jaringan kita untuk belajar suara dalam data pelatihan. Pada saat yang sama, dengan memungkinkan perpindahan besar, kami membuat jaringan kami lebih fleksibel dalam perilaku mereka - khususnya, perpindahan besar memfasilitasi saturasi neuron, yang kami inginkan. Untuk alasan ini, kami biasanya tidak memasukkan offset dalam regularisasi.

Teknik regularisasi lainnya

Ada banyak teknik regularisasi selain L2. Sebenarnya, sudah banyak teknik yang dikembangkan sehingga, dengan semua keinginan, saya tidak dapat menjelaskan semuanya secara singkat. Pada bagian ini, saya akan menjelaskan secara singkat tiga pendekatan lain untuk mengurangi pelatihan ulang: mengatur L1, keluar , dan secara artifisial meningkatkan set pelatihan. Kami tidak akan mempelajarinya sedalam topik sebelumnya. Sebagai gantinya, kita hanya mengenal mereka, dan pada saat yang sama menghargai beragam teknik regularisasi yang ada.

Regularisasi L1

Dalam pendekatan ini, kami memodifikasi fungsi biaya tidak teratur dengan menambahkan jumlah nilai absolut dari bobot:

$$

$$C = C_0 + \ frac {\ lambda} {n} \ sum_w | w | \ tag {95}$$

Secara intuitif, ini mirip dengan regularisasi L2, yang dikenakan untuk bobot besar dan membuat jaringan lebih memilih bobot rendah. Tentu saja, istilah regularisasi L1 tidak seperti istilah regularisasi L2, jadi Anda seharusnya tidak mengharapkan perilaku yang persis sama. Mari kita mencoba memahami bagaimana perilaku jaringan yang dilatih dengan regularisasi L1 berbeda dari jaringan yang dilatih dengan regularisasi L2.

Untuk melakukan ini, lihat turunan parsial dari fungsi biaya. Membedakan (95), kami memperoleh:

$$

$$\ frac {\ partial C} {\ partial w} = \ frac {\ partial C_0} {\ partial w} + \ frac {\ lambda} {n} \, {\ rm sgn} (w) \ tag {96 }$$

di mana sgn (w) adalah tanda w, yaitu, +1 jika w positif, dan -1 jika w negatif. Menggunakan ungkapan ini, kami sedikit memodifikasi propagasi belakang sehingga melakukan penurunan gradien stokastik menggunakan regularisasi L1. Aturan pembaruan terakhir untuk jaringan yang diatur L1:

$$

$$w \ rightarrow w '= w- \ frac {\ eta \ lambda} {n} \ mbox {sgn} (w) - \ eta \ frac {\ partial C_0} {\ partial w} \ tag {97}$$

di mana, seperti biasa, ∂C / ∂w dapat diperkirakan secara opsional menggunakan nilai rata-rata paket-mini. Bandingkan ini dengan aturan pembaruan regularisasi L2 (93):

$$

$$w \ rightarrow w '= w \ kiri (1 - \ frac {\ eta \ lambda} {n} \ kanan) - \ eta \ frac {\ partial C_0} {\ partial w} \ tag {98}$$

Dalam kedua ungkapan, efek regularisasi adalah mengurangi bobot. Ini bertepatan dengan gagasan intuitif bahwa kedua jenis regularisasi menghukum bobot yang besar. Namun, bobot dikurangi dengan cara yang berbeda. Dalam regularisasi L1, bobot berkurang dengan nilai konstan, cenderung ke 0. Dalam regularisasi L2, bobot berkurang dengan nilai yang sebanding dengan w. Oleh karena itu, ketika beberapa berat memiliki nilai besar | w |, regularisasi L1 mengurangi bobot tidak sebanyak L2. Begitu juga sebaliknya, saat | w | kecil, regularisasi L1 mengurangi berat badan jauh lebih banyak daripada regularisasi L2. Akibatnya, regularisasi L1 cenderung memusatkan bobot jaringan dalam jumlah yang relatif kecil dari ikatan penting, sedangkan bobot lainnya cenderung nol.

Saya sedikit merapikan satu masalah dalam diskusi sebelumnya - turunan parsial ∂C / ∂w tidak didefinisikan ketika w = 0. Ini karena fungsi | w | ada "ketegaran" akut pada titik w = 0, oleh karena itu, tidak dapat dibedakan di sana. Tapi ini tidak menakutkan. Kami hanya menerapkan aturan biasa, tidak teratur untuk penurunan gradien stokastik ketika w = 0. Secara intuitif, tidak ada yang salah dengan itu - regularisasi harus mengurangi bobot, dan jelas itu tidak dapat mengurangi bobot yang sudah sama dengan 0. Lebih tepatnya, kita akan menggunakan persamaan (96) dan (97) dengan kondisi sgn (0) = 0. Ini akan memberi kita aturan yang nyaman dan kompak untuk penurunan gradien stokastik dengan regularisasi L1.

Pengecualian [putus sekolah]

Pengecualian adalah teknik regularisasi yang sama sekali berbeda. Berbeda dengan regularisasi L1 dan L2, pengecualian tidak berurusan dengan perubahan fungsi biaya. Sebaliknya, kami mengubah jaringan itu sendiri. Izinkan saya menjelaskan mekanika dasar pengoperasian pengecualian sebelum mempelajari topik mengapa ia bekerja dan dengan hasil apa.

Misalkan kita mencoba untuk melatih jaringan:


Secara khusus, katakanlah kita memiliki input pelatihan x dan output yang diinginkan y. Biasanya, kita akan melatihnya dengan secara langsung mendistribusikan x melalui jaringan, dan kemudian kembali merambat untuk menentukan kontribusi gradien. Pengecualian mengubah proses ini. Kami mulai dengan secara acak dan sementara menghapus setengah dari neuron tersembunyi di jaringan, meninggalkan neuron input dan output tidak berubah. Setelah itu, kita akan memiliki kira-kira jaringan seperti itu. Perhatikan bahwa neuron yang dikecualikan, yang dikeluarkan sementara, masih ditandai dalam diagram:


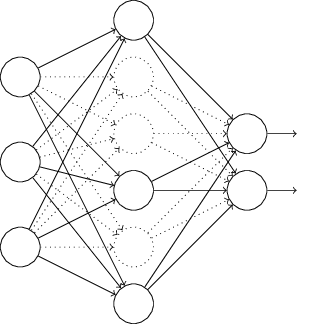
Kami melewati x dengan distribusi langsung melalui jaringan yang diubah, dan kemudian kembali mendistribusikan hasilnya, juga melalui jaringan yang diubah. Setelah kami melakukan ini dengan paket-mini contoh, kami memperbarui bobot dan offset yang sesuai. Kemudian kami ulangi proses ini, pertama mengembalikan neuron yang dikecualikan, kemudian memilih subset acak baru dari neuron tersembunyi untuk dihapus, mengevaluasi gradien untuk paket-mini lainnya, dan memperbarui bobot dan offset jaringan.

Mengulangi proses ini berulang-ulang, kami mendapatkan jaringan yang telah mempelajari beberapa bobot dan perpindahan. Secara alami, bobot dan perpindahan ini dipelajari dalam kondisi di mana setengah dari neuron yang tersembunyi dikeluarkan.Dan ketika kita meluncurkan jaringan secara penuh, kita akan memiliki dua kali lipat neuron tersembunyi aktif. Untuk mengimbangi ini, kami membagi dua bobot yang berasal dari neuron tersembunyi.

Prosedur pengecualian mungkin tampak aneh dan sewenang-wenang. Mengapa dia harus membantu dengan regularisasi? Untuk menjelaskan apa yang terjadi, saya ingin Anda melupakan pengecualian untuk sementara waktu dan memberikan pelatihan Majelis Nasional dengan cara standar. Secara khusus, bayangkan bahwa kami melatih beberapa NS yang berbeda menggunakan data pelatihan yang sama. Tentu saja, jaringan dapat bervariasi pada awalnya, dan kadang-kadang pelatihan dapat memberikan hasil yang berbeda. Dalam kasus seperti itu, kita dapat menerapkan semacam skema rata-rata atau pemungutan suara untuk memutuskan output mana yang akan diterima. Misalnya, jika kita melatih lima jaringan, dan tiga di antaranya mengklasifikasikan angka tersebut sebagai "3," maka ini mungkin tiga yang benar. Dan dua jaringan lainnya mungkin salah. Skema rata-rata seperti itu seringkali merupakan cara yang berguna (walaupun mahal) untuk mengurangi pelatihan ulang. Alasannya adalahbahwa jaringan yang berbeda dapat berlatih kembali dengan cara yang berbeda, dan rata-rata dapat membantu menghilangkan pelatihan ulang tersebut.

Bagaimana semua ini berhubungan dengan pengecualian? Secara heuristik, ketika kami mengecualikan set neutron yang berbeda, seolah-olah kami melatih NS yang berbeda. Oleh karena itu, prosedur pengecualian mirip dengan efek rata-rata pada sejumlah besar jaringan yang berbeda. Jaringan yang berbeda dilatih ulang dengan cara yang berbeda, sehingga diharapkan efek rata-rata pengecualian akan mengurangi pelatihan ulang.

Penjelasan heuristik terkait tentang manfaat pengecualian diberikan dalam salah satu karya paling awalmenggunakan teknik ini: “Teknik ini mengurangi adaptasi sendi yang kompleks dari neuron, karena neuron tidak dapat bergantung pada kehadiran tetangga tertentu. Pada akhirnya, ia harus mempelajari sifat-sifat yang lebih andal yang dapat berguna dalam bekerja bersama dengan banyak subset neuron acak yang berbeda. ” Dengan kata lain, jika kita membayangkan Majelis Nasional kita sebagai suatu model yang membuat prediksi, maka pengecualian akan menjadi cara untuk menjamin stabilitas model tersebut dengan hilangnya bagian-bagian bukti individual. Dalam hal ini, tekniknya menyerupai regularisasi L1 dan L2, yang berusaha mengurangi bobot, dan dengan cara ini membuat jaringan lebih tahan terhadap kehilangan koneksi individu dalam jaringan.

Secara alami, ukuran sebenarnya dari manfaat pengecualian adalah keberhasilannya yang luar biasa dalam meningkatkan efisiensi jaringan saraf. Dalam karya aslinyadi mana metode ini diperkenalkan, itu diterapkan pada banyak tugas berbeda. Kami sangat tertarik pada kenyataan bahwa penulis menerapkan pengecualian pada klasifikasi angka dari MNIST, menggunakan jaringan distribusi langsung sederhana mirip dengan yang kami periksa. Makalah ini mencatat bahwa sampai saat itu, hasil terbaik untuk arsitektur seperti itu adalah akurasi 98,4%. Mereka meningkatkannya menjadi 98,7% menggunakan kombinasi pengecualian dan bentuk modifikasi dari regularisasi L2. Hasil yang sama mengesankannya diperoleh untuk banyak tugas lain, termasuk pengenalan pola dan ucapan, dan pemrosesan bahasa alami. Pengecualian ini sangat berguna dalam pelatihan jaringan dalam yang besar, di mana masalah pelatihan ulang sering muncul.

Set data pelatihan yang diperluas secara artifisial

Kami melihat sebelumnya bahwa akurasi klasifikasi MNIST kami turun menjadi 80 persen, ketika kami hanya menggunakan 1.000 gambar pelatihan. Dan tidak heran - dengan lebih sedikit data, jaringan kami akan memenuhi lebih sedikit opsi untuk menulis angka oleh orang-orang. Mari kita coba latih jaringan kami dari 30 neuron tersembunyi, menggunakan volume pelatihan yang berbeda untuk melihat perubahan efisiensi. Kami berlatih menggunakan ukuran paket mini 10, kecepatan belajar η = 0,5, parameter regularisasi λ = 5.0, dan fungsi biaya dengan cross entropy. Kami akan melatih jaringan 30 era menggunakan set data lengkap, dan meningkatkan jumlah era secara proporsional dengan penurunan volume data pelatihan. Untuk menjamin faktor penurunan berat badan yang sama untuk set data pelatihan yang berbeda, kami akan menggunakan parameter regularisasi λ = 5,0 dengan set pelatihan lengkap, dan menguranginya secara proporsional dengan penurunan volume data.


Dapat dilihat bahwa akurasi klasifikasi tumbuh secara signifikan dengan meningkatnya data pelatihan. Pertumbuhan ini kemungkinan akan berlanjut dengan peningkatan volume lebih lanjut. Tentu saja, dilihat dari grafik di atas, kita sedang mendekati saturasi. Namun, misalkan kita mengulang grafik ini menjadi ketergantungan logaritmik pada jumlah data pelatihan:


Dapat dilihat bahwa pada akhirnya grafik masih cenderung naik. Ini menunjukkan bahwa jika kita mengambil jumlah data yang jauh lebih besar - misalnya, jutaan atau bahkan miliaran contoh tulisan tangan, daripada 50.000 - maka kita mungkin akan mendapatkan jaringan kerja yang jauh lebih baik bahkan dari ukuran sekecil itu.

Mendapatkan lebih banyak data pelatihan adalah ide bagus. Sayangnya, ini bisa mahal, jadi dalam praktiknya tidak selalu mungkin. Namun, ada ide lain yang dapat bekerja hampir sama - secara artifisial meningkatkan kumpulan data. Sebagai contoh, misalkan kita mengambil gambar lima dari MNIST, dan memutarnya sedikit, derajat 15:



Ini jelas angka yang sama. Tetapi pada tingkat piksel, ini sangat berbeda dari gambar yang tersedia di database MNIST. Masuk akal untuk mengasumsikan bahwa menambahkan gambar ini ke dataset pelatihan dapat membantu jaringan kami mempelajari lebih lanjut tentang klasifikasi gambar. Selain itu, kami jelas tidak terbatas pada kemampuan untuk menambahkan hanya satu gambar. Kami dapat memperluas data pelatihan kami dengan membuat beberapa belokan kecil dari semua gambar pelatihan dari MNIST, dan kemudian menggunakan rangkaian data pelatihan yang diperluas untuk meningkatkan efisiensi jaringan.

Ide ini sangat kuat, dan digunakan secara luas. Mari kita lihat hasil dari karya ilmiahyang menerapkan beberapa variasi ide ini ke MNIST. Salah satu arsitektur jaringan yang dipertimbangkan oleh mereka mirip dengan yang kami gunakan - jaringan distribusi langsung dengan 800 neuron tersembunyi, menggunakan fungsi biaya dengan cross entropy. Dengan meluncurkan jaringan ini dengan set pelatihan MNIST standar, mereka memperoleh akurasi klasifikasi 98,4%. Tapi kemudian mereka memperluas data pelatihan, tidak hanya menggunakan rotasi yang saya jelaskan di atas, tetapi juga transfer dan distorsi gambar. Setelah melatih jaringan pada data tingkat lanjut, mereka meningkatkan keakuratannya menjadi 98,9%. Mereka juga bereksperimen dengan apa yang disebut "Elastic distortion", jenis khusus dari distorsi gambar, dirancang untuk menghilangkan getaran acak dari otot-otot tangan. Menggunakan distorsi elastis untuk memperluas data, mereka mencapai akurasi 99,3%. Intinya, mereka memperluas pengalaman jaringan mereka,memberinya berbagai variasi tulisan tangan yang ditemukan dalam tulisan tangan asli.

Varian dari ide ini dapat digunakan untuk meningkatkan kinerja banyak tugas belajar, tidak hanya untuk pengenalan tulisan tangan. Prinsip umum adalah memperluas data pelatihan dengan menerapkan operasi pada mereka yang mencerminkan variasi yang ditemui dalam kenyataan. Variasi seperti itu mudah dibuat. Misalkan kita membuat NS untuk pengenalan ucapan. Orang-orang dapat mengenali pembicaraan bahkan dengan distorsi seperti kebisingan latar belakang. Oleh karena itu, Anda dapat memperluas data dengan menambahkan noise latar belakang. Kami juga mampu mengenali pembicaraan yang dipercepat dan lambat. Ini adalah cara lain untuk memperluas data pelatihan. Teknik-teknik ini tidak selalu digunakan - misalnya, alih-alih memperluas set pelatihan dengan menambahkan noise, mungkin lebih efisien untuk membersihkan input dengan menerapkan filter noise pada mereka. Namun, ada baiknya mengingat gagasan memperluas set pelatihan,dan mencari cara untuk menggunakannya.

Latihan

• Seperti yang kita diskusikan di atas, salah satu cara untuk memperluas data pelatihan dari MNIST adalah dengan menggunakan rotasi kecil dari gambar-gambar pelatihan. Masalah apa yang bisa muncul jika kita mengizinkan rotasi gambar di sudut mana pun?

Penyimpangan data besar dan arti membandingkan akurasi klasifikasi

Mari kita lihat lagi bagaimana keakuratan NS kami bervariasi tergantung pada ukuran set pelatihan:


Misalkan alih-alih menggunakan NS kita akan menggunakan teknologi pembelajaran mesin lain untuk mengklasifikasikan angka. Misalnya, mari kita coba menggunakan metode mesin vektor dukungan (SVM), yang kami temui secara singkat di bab 1. Saat itu, jangan khawatir jika Anda tidak terbiasa dengan SVM, kami tidak perlu memahami detailnya. Kami akan menggunakan SVM melalui perpustakaan scikit-learn. Berikut adalah bagaimana efektivitas SVM bervariasi dengan ukuran set pelatihan. Sebagai perbandingan, saya memasukkan jadwal dan hasil Majelis Nasional.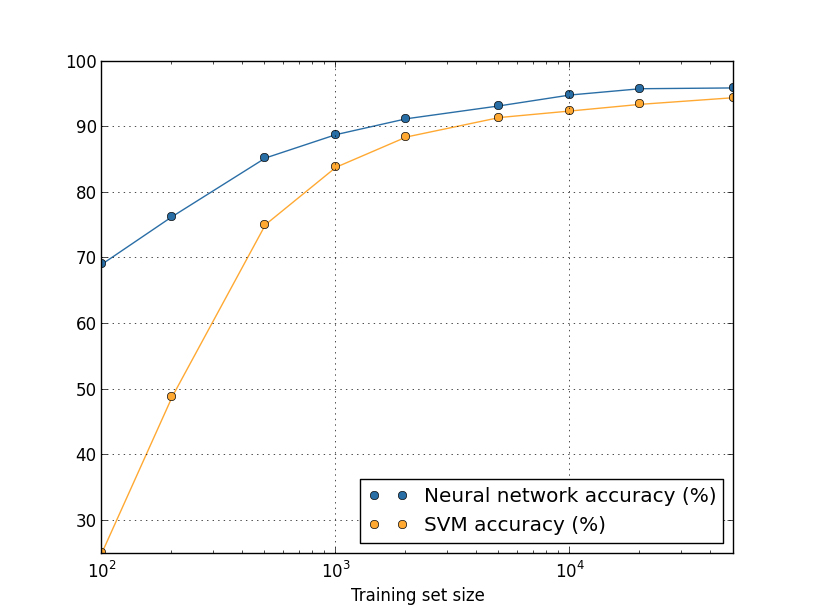


Mungkin hal pertama yang menarik perhatian Anda - NS melampaui SVM dalam ukuran pelatihan apa pun. Ini bagus, meskipun tidak layak menarik kesimpulan yang jauh dari ini, karena saya menggunakan pengaturan scikit-belajar yang telah ditentukan, dan kami bekerja cukup serius di NS kami. Fakta yang kurang jelas, tetapi lebih menarik, yang mengikuti dari grafik, adalah bahwa jika kita melatih SVM kita menggunakan 50.000 gambar, itu akan bekerja lebih baik (akurasi 94,48%) daripada NS kami dilatih dengan 5000 gambar ( 93,24%). Dengan kata lain, peningkatan volume data pelatihan kadang-kadang mengimbangi perbedaan dalam algoritma MO.

Sesuatu yang lebih menarik mungkin terjadi. Misalkan kita sedang mencoba untuk menyelesaikan masalah menggunakan dua algoritma MO, A dan B. Kadang-kadang terjadi bahwa algoritma A berada di depan algoritma B pada satu set data pelatihan, dan algoritma B berada di depan algoritma A pada kumpulan data pelatihan lainnya. Kami tidak melihat ini di atas - maka grafik akan berpotongan - tetapi ini terjadi . Jawaban yang benar untuk pertanyaan: "Apakah algoritma A lebih unggul dari algoritma B?" sebenarnya, ini: "Apa dataset pelatihan yang Anda gunakan?"

Semua ini harus diperhitungkan, baik selama pengembangan dan saat membaca karya ilmiah. Banyak karya berkonsentrasi pada menemukan trik baru untuk memeras hasil yang lebih baik pada set data pengukuran standar. "Teknologi makanan super kami memberi kami peningkatan X% pada set komparatif standar Y" - formulir aplikasi kanonik dalam penelitian tersebut. Terkadang pernyataan seperti itu sebenarnya menarik, tetapi perlu dipahami bahwa pernyataan itu hanya berlaku dalam konteks rangkaian pelatihan tertentu. Bayangkan sebuah cerita alternatif di mana orang-orang yang awalnya membuat set komparatif menerima dana penelitian yang lebih besar. Mereka dapat menggunakan uang ekstra untuk mengumpulkan data tambahan. Ada kemungkinan bahwa "peningkatan" teknologi super-duper akan hilang pada dataset yang lebih besar. Dengan kata lain,esensi dari perbaikan mungkin hanya kecelakaan. Dari ini, moralitas berikut harus dibawa ke bidang aplikasi praktis: kita membutuhkan algoritma yang ditingkatkan dan data pelatihan yang ditingkatkan. Tidak ada yang salah dengan mencari algoritma yang ditingkatkan, tetapi pastikan Anda tidak berkonsentrasi pada hal ini, mengabaikan cara yang lebih mudah untuk menang dengan meningkatkan volume atau kualitas data pelatihan.

Tantangan

• . ? . – , , , . , . - ? , .

Ringkasan

Kami telah menyelesaikan pencelupan kami dalam pelatihan ulang dan regularisasi. Tentu saja, kami akan kembali ke masalah ini. Seperti yang telah saya sebutkan beberapa kali, pelatihan ulang adalah masalah besar di bidang NS, terutama karena komputer menjadi lebih kuat dan kita dapat melatih jaringan yang lebih besar. Akibatnya, ada kebutuhan mendesak untuk mengembangkan teknik regularisasi yang efektif untuk mengurangi pelatihan ulang, sehingga bidang ini sangat aktif saat ini.

Inisialisasi Berat

Ketika kita membuat NS kita, kita perlu membuat pilihan nilai awal bobot dan offset. Sejauh ini, kami telah memilihnya sesuai dengan pedoman yang dijelaskan secara singkat di Bab 1. Saya ingat bahwa kami memilih bobot dan offset berdasarkan distribusi Gaussian independen dengan ekspektasi matematis 0 dan standar deviasi 1. Pendekatan ini bekerja dengan baik, tetapi tampaknya agak sewenang-wenang, jadi itu sangat berharga, merevisinya dan berpikir apakah mungkin untuk menemukan cara yang lebih baik untuk menetapkan bobot dan perpindahan awal, dan, mungkin, membantu NS kami belajar lebih cepat.

Ternyata proses inisialisasi dapat ditingkatkan secara serius dibandingkan dengan distribusi Gaussian yang dinormalisasi. Untuk memahami ini, katakanlah kita bekerja dengan jaringan dengan sejumlah besar neuron input, katakanlah, dari 1000. Dan katakanlah kita menggunakan distribusi Gaussian yang dinormalisasi untuk menginisialisasi bobot yang terhubung ke lapisan tersembunyi pertama. Sejauh ini, saya hanya akan fokus pada skala yang menghubungkan neuron input ke neuron pertama di lapisan tersembunyi, dan mengabaikan sisa jaringan:


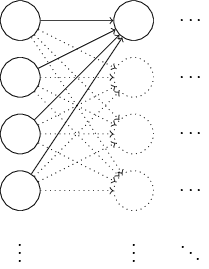
Untuk kesederhanaan, mari kita bayangkan bahwa kita mencoba untuk melatih jaringan dengan input x, di mana setengah dari neuron input dihidupkan, yaitu, mereka memiliki nilai 1, dan setengahnya dimatikan, yaitu, mereka memiliki nilai 0. Argumen berikutnya bekerja dalam kasus yang lebih umum, tetapi lebih mudah bagi Anda akan mengerti dia tentang contoh khusus ini. Pertimbangkan jumlah tertimbang z = wjwjxj + b input untuk neuron tersembunyi. 500 anggota dari jumlah menghilang karena xj yang sesuai adalah 0. Oleh karena itu, z adalah jumlah dari 501 variabel acak Gaussian yang dinormalisasi, 500 bobot, dan 1 offset tambahan. Oleh karena itu, nilai z itu sendiri memiliki distribusi Gaussian dengan ekspektasi matematika 0 dan standar deviasi √501 ≈ 22,4. Artinya, z memiliki distribusi Gaussian yang cukup luas, tanpa puncak yang tajam:


Secara khusus, grafik ini menunjukkan bahwa | z | cenderung cukup besar, yaitu, z ≫ 1 atau z ≫ -1. Dalam hal ini, output dari neuron tersembunyi σ (z) akan sangat dekat dengan 1 atau 0. Ini berarti bahwa neuron tersembunyi kita akan jenuh. Dan ketika ini terjadi, seperti yang sudah kita ketahui, perubahan kecil dalam bobot akan menghasilkan perubahan kecil dalam aktivasi neuron tersembunyi. Perubahan kecil ini, pada gilirannya, praktis tidak akan mempengaruhi neutron yang tersisa dalam jaringan, dan kita akan melihat perubahan kecil terkait fungsi biaya. Akibatnya, bobot ini akan dilatih sangat lambat ketika kita menggunakan algoritma gradient descent. Ini mirip dengan tugas yang telah kita bahas dalam bab ini, di mana neuron keluaran jenuh dengan nilai-nilai yang salah menyebabkan pembelajaran melambat. Kami biasa mengatasi masalah ini dengan secara cerdik memilih fungsi biaya. Sayangnya, meskipun ini membantu dengan neuron output jenuh, itu tidak membantu sama sekali dengan saturasi neuron tersembunyi.

Sekarang saya berbicara tentang skala yang masuk dari lapisan tersembunyi pertama. Tentu saja, argumen yang sama berlaku untuk lapisan tersembunyi berikut: jika bobot dalam lapisan tersembunyi kemudian diinisialisasi menggunakan distribusi Gaussian yang dinormalisasi, aktivasi mereka akan sering mendekati 0 atau 1, dan pelatihan akan berjalan sangat lambat.

Apakah ada cara untuk memilih opsi inisialisasi terbaik untuk bobot dan offset, sehingga kita tidak mendapatkan kejenuhan seperti itu, dan dapat menghindari belajar keterlambatan? Misalkan kita memiliki neuron dengan jumlah bobot masuk n. Maka kita perlu menginisialisasi bobot ini dengan distribusi Gaussian acak dengan ekspektasi matematika 0 dan deviasi standar 1 / √ n _in . Artinya, kita menekan Gaussians, dan mengurangi kemungkinan saturasi neuron. Kemudian kita akan memilih distribusi Gaussian untuk perpindahan dengan ekspektasi matematis 0 dan standar deviasi 1, dengan alasan bahwa saya akan kembali lagi nanti. Setelah membuat pilihan ini, kita kembali menemukan bahwa z = w _{jw j} x _j + b akan menjadi variabel acak dengan distribusi Gaussian dengan ekspektasi matematis 0, tetapi dengan puncak yang jauh lebih jelas daripada sebelumnya. Misalkan, seperti sebelumnya, bahwa 500 input adalah 0 dan 500 adalah 1. Maka mudah untuk menunjukkan (lihat latihan di bawah ini) bahwa z memiliki distribusi Gaussian dengan ekspektasi matematis 0 dan standar deviasi √ (3/2) = 1.22 ... Grafik ini memiliki puncak yang jauh lebih tajam, sedemikian rupa sehingga bahkan dalam gambar di bawah situasinya sedikit dikecilkan, karena saya harus mengubah skala sumbu vertikal dibandingkan dengan grafik sebelumnya:


Neuron semacam itu akan jenuh dengan probabilitas yang jauh lebih rendah, dan, karenanya, kemungkinan kecil akan mengalami penurunan dalam pembelajaran.

Latihan

• Konfirmasikan bahwa standar deviasi z = ∑ _{jw j} x _j + b dari paragraf sebelumnya adalah √ (3/2). Pertimbangan yang mendukung ini: varians dari jumlah variabel acak independen sama dengan jumlah varian variabel acak individu; variansnya sama dengan kuadrat dari deviasi standar.

Saya sebutkan di atas bahwa kita akan terus menginisialisasi perpindahan, seperti sebelumnya, berdasarkan pada distribusi Gaussian yang independen dengan ekspektasi matematis 0 dan standar deviasi 1. Dan ini normal, karena tidak banyak meningkatkan kemungkinan saturasi neuron kita. Sebenarnya, inisialisasi offset tidak terlalu menjadi masalah jika kita berhasil menghindari masalah saturasi. Beberapa bahkan mencoba untuk menginisialisasi semua offset ke nol, dan mengandalkan fakta bahwa gradient descent dapat mempelajari offset yang sesuai. Tetapi karena kemungkinan ini akan mempengaruhi sesuatu yang kecil, kami akan terus menggunakan prosedur inisialisasi yang sama seperti sebelumnya.

Mari kita bandingkan hasil dari pendekatan lama dan baru untuk menginisialisasi bobot menggunakan tugas mengklasifikasikan angka dari MNIST. Seperti sebelumnya, kita akan menggunakan 30 neuron tersembunyi, paket mini ukuran 10, parameter regularisasi & lambda = 5.0, dan fungsi biaya dengan cross entropy. Kami akan secara bertahap mengurangi kecepatan belajar dari η = 0,5 menjadi 0,1, karena dengan cara ini hasilnya akan sedikit lebih baik terlihat pada grafik. Anda dapat belajar menggunakan metode inisialisasi berat yang lama:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

Anda juga dapat belajar menggunakan pendekatan baru untuk menginisialisasi bobot. Ini bahkan lebih sederhana, karena secara default network2 menginisialisasi bobot menggunakan pendekatan baru. Ini berarti bahwa kami dapat menghilangkan panggilan net.large_weight_initializer () sebelumnya:

 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

Kami memplot (menggunakan program weight_initialization.py):


Dalam kedua kasus, akurasi klasifikasi 96% diperoleh. Akurasi yang dihasilkan hampir sama dalam kedua kasus. Tetapi teknik inisialisasi baru mencapai titik ini jauh lebih cepat. Pada akhir era terakhir pelatihan, pendekatan lama untuk menginisialisasi bobot mencapai akurasi 87%, dan pendekatan baru sudah mendekati 93%. Rupanya, pendekatan baru untuk menginisialisasi bobot dimulai dari posisi yang jauh lebih baik, sehingga kami mendapatkan hasil yang baik lebih cepat. Fenomena yang sama diamati jika kita membangun hasil untuk jaringan dengan 100 neuron:


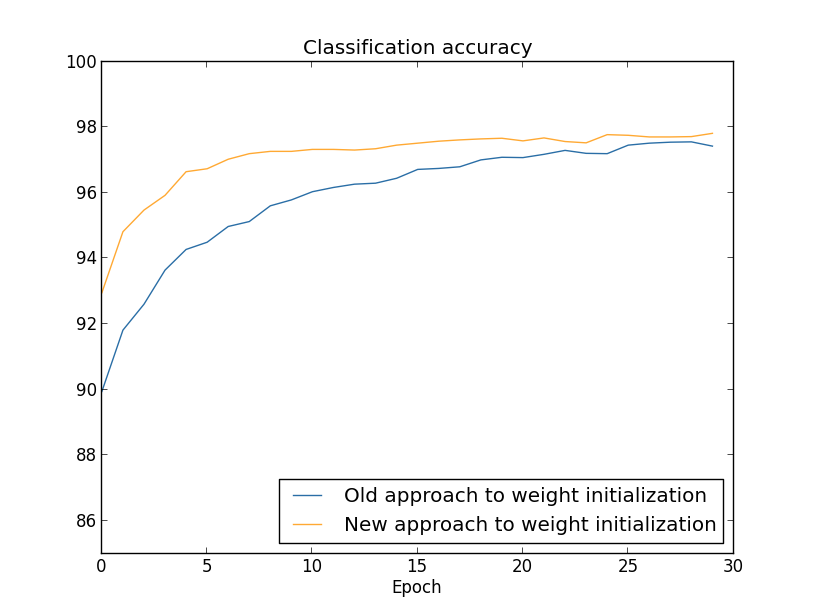
Dalam hal ini, dua kurva tidak terjadi. Namun, percobaan saya mengatakan bahwa jika Anda menambahkan sedikit lebih banyak era, maka keakuratannya mulai hampir bersamaan. Oleh karena itu, berdasarkan percobaan ini, kita dapat mengatakan bahwa meningkatkan inisialisasi bobot hanya mempercepat pelatihan, tetapi tidak mengubah efisiensi jaringan secara keseluruhan. Namun, dalam bab 4 kita akan melihat contoh NS di mana efisiensi jangka panjang meningkat secara signifikan sebagai akibat dari inisialisasi bobot melalui 1 / √ n _in . Oleh karena itu, tidak hanya meningkatkan kecepatan belajar, tetapi kadang-kadang efektivitas yang dihasilkan.

Pendekatan untuk menginisialisasi bobot melalui 1 / √n _dalam membantu meningkatkan pelatihan jaringan saraf. Teknik-teknik lain untuk menginisialisasi bobot telah diusulkan, banyak di antaranya didasarkan pada ide dasar ini. Saya tidak akan mempertimbangkannya di sini, karena 1 / inn bekerja dengan baik untuk tujuan kita. Jika Anda tertarik, saya sarankan membaca diskusi di halaman 14 dan 15 di sebuah makalah 2012 oleh Yoshua Benggio.

Tantangan

• Kombinasi regularisasi dan metode inisialisasi berat badan ditingkatkan. Kadang-kadang regularisasi L2 secara otomatis memberi kita hasil yang mirip dengan metode baru inisialisasi bobot. Katakanlah kita menggunakan pendekatan lama untuk menginisialisasi bobot. Buat garis besar argumen heuristik yang membuktikan bahwa: (1) jika λ tidak terlalu kecil, maka pada zaman pelatihan pertama, pelemahan bobot akan mendominasi hampir sepenuhnya; (2) jika ηλ ≪ n, maka bobot akan melemah e ^{−ηλ / m} kali dalam zaman; (3) jika λ tidak terlalu besar, melemahnya bobot akan melambat ketika bobot turun menjadi sekitar 1 / √ n, di mana n adalah jumlah total bobot dalam jaringan. Buktikan bahwa syarat-syarat ini dipenuhi dalam contoh-contoh yang grafiknya dibangun di bagian ini.

Kembali ke pengenalan tulisan tangan: kode

Mari menerapkan ide-ide yang dijelaskan dalam bab ini. Kami akan mengembangkan program baru, network2.py, versi yang lebih baik dari program network.py yang kami buat di bab 1. Jika Anda belum melihat kodenya untuk waktu yang lama, Anda mungkin perlu dengan cepat membahasnya. Ini hanya 74 baris kode, dan mudah dimengerti.

Seperti halnya network.py, bintang dari network2.py adalah kelas Jaringan, yang kami gunakan untuk mewakili NS kami. Kami menginisialisasi instance kelas dengan daftar ukuran lapisan jaringan yang sesuai, dan dengan pilihan fungsi biaya, secara default akan menjadi lintas entropi:

 class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost 

Beberapa baris pertama dari metode __init__ sama dengan network.py, dan dipahami sendiri. Dua baris berikutnya adalah baru, dan kita perlu memahami secara rinci apa yang mereka lakukan.

Mari kita mulai dengan metode default_weight_initializer. Dia menggunakan pendekatan baru yang ditingkatkan untuk menginisialisasi bobot. Seperti yang telah kita lihat, dalam pendekatan ini, bobot memasuki neuron diinisialisasi berdasarkan distribusi Gaussian independen dengan ekspektasi matematis 0 dan deviasi standar 1 dibagi dengan akar kuadrat dari jumlah tautan yang masuk ke neuron. Juga, metode ini akan menginisialisasi offset menggunakan distribusi Gaussian dengan rata-rata 0 dan standar deviasi 1. Berikut adalah kodenya:

  def default_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] 

Untuk memahaminya, Anda harus ingat bahwa np adalah perpustakaan Numpy yang berurusan dengan aljabar linier. Kami mengimpornya di awal program. Perhatikan juga bahwa kami tidak menginisialisasi perpindahan di lapisan pertama neuron. Lapisan pertama adalah inbound, jadi offset tidak digunakan. Yang sama adalah network.py.

Selain metode default_weight_initializer, kami akan membuat metode large_weight_initializer. Ini menginisialisasi bobot dan offset menggunakan pendekatan lama dari Bab 1, di mana bobot dan offset diinisialisasi berdasarkan distribusi Gaussian independen dengan ekspektasi matematis 0 dan standar deviasi 1. Kode ini, tentu saja, tidak jauh berbeda dari default_weight_initializer:

  def large_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] 

Saya memasukkan metode ini terutama karena lebih mudah bagi kami untuk membandingkan hasil dari bab dan bab 1. Saya tidak bisa membayangkan opsi nyata yang saya sarankan untuk menggunakannya!

Kebaruan kedua dari metode __init__ akan menjadi inisialisasi atribut biaya. Untuk memahami cara kerjanya, mari kita lihat kelas yang kita gunakan untuk merepresentasikan fungsi biaya lintas-entropi (direktif @staticmethod memberi tahu juru bahasa bahwa metode ini tidak tergantung pada objek, sehingga parameter mandiri tidak diteruskan ke metode fn dan delta).

 class CrossEntropyCost(object): @staticmethod def fn(a, y): return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): return (ay) 

Mari kita cari tahu. Hal pertama yang dapat dilihat di sini adalah bahwa, meskipun cross entropy adalah fungsi dari sudut pandang matematika, kami mengimplementasikannya sebagai kelas python, bukan fungsi python. Mengapa saya memutuskan untuk melakukan ini? Di jaringan kami, nilai memainkan dua peran yang berbeda. Jelas - ini adalah ukuran seberapa baik aktivasi output sesuai dengan output yang diinginkan y. Peran ini disediakan oleh metode CrossEntropyCost.fn. (Omong-omong, perhatikan bahwa memanggil np.nan_to_num di dalam CrossEntropyCost.fn memastikan bahwa Numpy memproses logaritma angka yang mendekati nol dengan benar). Namun, fungsi biaya digunakan dalam jaringan kami dengan cara kedua. Kita ingat dari Bab 2 bahwa ketika memulai algoritma backpropagation, kita perlu mempertimbangkan kesalahan output dari jaringan δ ^L. Bentuk kesalahan output tergantung pada fungsi biaya: fungsi biaya yang berbeda akan memiliki bentuk kesalahan output yang berbeda. Untuk cross entropy, kesalahan output, seperti yang berikut dari persamaan (66), akan sama dengan:

$$

$$\ delta ^ L = a ^ L-y \ tag {99}$$

Oleh karena itu, saya mendefinisikan metode kedua, CrossEntropyCost.delta, yang tujuannya adalah untuk menjelaskan kepada jaringan cara menghitung kesalahan output. Dan kemudian kami menggabungkan kedua metode ini ke dalam satu kelas yang berisi segala sesuatu yang perlu diketahui jaringan kami tentang fungsi biaya.

Untuk alasan yang sama, network2.py berisi kelas yang mewakili fungsi biaya kuadratik. Termasuk ini untuk perbandingan dengan hasil Bab 1, karena di masa depan kita terutama akan menggunakan cross entropy. Kode di bawah. Metode QuadraticCost.fn adalah perhitungan sederhana biaya kuadratik yang terkait dengan output a dan output y yang diinginkan. Nilai yang dikembalikan oleh QuadraticCost.delta didasarkan pada ekspresi (30) untuk kesalahan output dari nilai kuadratik, yang kami peroleh pada Bab 2.

 class QuadraticCost(object): @staticmethod def fn(a, y): return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): return (ay) * sigmoid_prime(z) 

Sekarang kami telah menemukan perbedaan utama antara network2.py dan network2.py. Semuanya sangat sederhana. Ada perubahan kecil lain yang akan saya jelaskan di bawah ini, termasuk implementasi regularisasi L2. Sebelum itu, mari kita lihat kode network2.py lengkap. Tidak perlu mempelajarinya secara rinci, tetapi perlu memahami struktur dasar, khususnya, membaca komentar untuk memahami apa yang masing-masing bagian dari program lakukan. Tentu saja, saya tidak melarang mempelajari pertanyaan ini sebanyak yang Anda suka! Jika Anda tersesat, coba baca teks setelah program, dan kembali ke kode lagi. Secara umum, ini dia:

 """network2.py ~~~~~~~~~~~~~~   network.py,            .   –      , ,   .     ,    .   ,       . """ ####  #  import json import random import sys #  import numpy as np ####   ,      class QuadraticCost(object): @staticmethod def fn(a, y): """ ,    ``a``    ``y``. """ return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): """  delta   .""" return (ay) * sigmoid_prime(z) class CrossEntropyCost(object): @staticmethod def fn(a, y): """ ,    ``a``    ``y``. np.nan_to_num    .  ,   ``a``  ``y``      1.0,   (1-y)*np.log(1-a)  nan. np.nan_to_num ,       (0.0). """ return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): """  delta   .  ``z``    ,          delta     . """ return (ay) ####   Network class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].       ,   ``self.default_weight_initializer`` (.  ). """ self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost def default_weight_initializer(self): """            0    1,       ,       .          0    1.    ,         ,           . """ self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def large_weight_initializer(self): """          0    1.          0    1.    ,         ,           .         1,    .       . """ self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def feedforward(self, a): """  ,  ``a``  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, lmbda = 0.0, evaluation_data=None, monitor_evaluation_cost=False, monitor_evaluation_accuracy=False, monitor_training_cost=False, monitor_training_accuracy=False): """     -    . ``training_data`` –   ``(x, y)``,       .       ,    ``lmbda``.    ``evaluation_data``,     ,   .         ,     ,   .      :   ,    ,   ,              .  ,      30 ,        30 ,        .     ,   . """ if evaluation_data: n_data = len(evaluation_data) n = len(training_data) evaluation_cost, evaluation_accuracy = [], [] training_cost, training_accuracy = [], [] for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch( mini_batch, eta, lmbda, len(training_data)) print "Epoch %s training complete" % j if monitor_training_cost: cost = self.total_cost(training_data, lmbda) training_cost.append(cost) print "Cost on training data: {}".format(cost) if monitor_training_accuracy: accuracy = self.accuracy(training_data, convert=True) training_accuracy.append(accuracy) print "Accuracy on training data: {} / {}".format( accuracy, n) if monitor_evaluation_cost: cost = self.total_cost(evaluation_data, lmbda, convert=True) evaluation_cost.append(cost) print "Cost on evaluation data: {}".format(cost) if monitor_evaluation_accuracy: accuracy = self.accuracy(evaluation_data) evaluation_accuracy.append(accuracy) print "Accuracy on evaluation data: {} / {}".format( self.accuracy(evaluation_data), n_data) print return evaluation_cost, evaluation_accuracy, \ training_cost, training_accuracy def update_mini_batch(self, mini_batch, eta, lmbda, n): """    ,          -. ``mini_batch`` –    ``(x, y)``, ``eta`` –  , ``lmbda`` -  , ``n`` -     .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) # backward pass delta = (self.cost).delta(zs[-1], activations[-1], y) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """  l      ,      . l = 1    , l = 2 – ,   .    ,   python      . """ for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def accuracy(self, data, convert=False): """    ``data``,      .   –        .  ``convert``  False,    –    ( )  True,   .    - ,  ``y`` -     .  ,       .           .          ?     –       ,      .   ,      .       mnist_loader.load_data_wrapper. """ if convert: results = [(np.argmax(self.feedforward(x)), np.argmax(y)) for (x, y) in data] else: results = [(np.argmax(self.feedforward(x)), y) for (x, y) in data] return sum(int(x == y) for (x, y) in results) def total_cost(self, data, lmbda, convert=False): """      ``data``.  ``convert``   False,   –  (),   True,   –   . .    ,      ``accuracy``, . """ cost = 0.0 for x, y in data: a = self.feedforward(x) if convert: y = vectorized_result(y) cost += self.cost.fn(a, y)/len(data) cost += 0.5*(lmbda/len(data))*sum( np.linalg.norm(w)**2 for w in self.weights) return cost def save(self, filename): """    ``filename``.""" data = {"sizes": self.sizes, "weights": [w.tolist() for w in self.weights], "biases": [b.tolist() for b in self.biases], "cost": str(self.cost.__name__)} f = open(filename, "w") json.dump(data, f) f.close() ####  Network def load(filename): """    ``filename``.    Network. """ f = open(filename, "r") data = json.load(f) f.close() cost = getattr(sys.modules[__name__], data["cost"]) net = Network(data["sizes"], cost=cost) net.weights = [np.array(w) for w in data["weights"]] net.biases = [np.array(b) for b in data["biases"]] return net ####   def vectorized_result(j): """  10-    1.0   j     .      (0..9)     . """ e = np.zeros((10, 1)) e[j] = 1.0 return e def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

Di antara perubahan yang lebih menarik adalah dimasukkannya regularisasi L2. Meskipun ini adalah perubahan konseptual yang besar, sangat mudah untuk diterapkan sehingga Anda mungkin tidak melihatnya dalam kode. Sebagian besar, ini hanya melewatkan parameter lmbda ke metode yang berbeda, terutama Network.SGD. Semua pekerjaan dilakukan dalam satu baris program, yang keempat dari akhir dalam metode Network.update_mini_batch. Di sana kami mengubah aturan pembaruan gradient descent untuk memasukkan pengurangan berat. Perubahannya kecil, tetapi sangat memengaruhi hasil!

Omong-omong, ini sering terjadi ketika menerapkan teknik baru dalam jaringan saraf. Kami menghabiskan ribuan kata untuk membahas regularisasi. Secara konseptual, ini adalah hal yang cukup halus dan sulit dipahami. Namun, ini dapat ditambahkan secara sepele ke dalam program! Tanpa diduga, teknik kompleks dapat diimplementasikan dengan perubahan kode kecil.

Perubahan kecil tapi penting lainnya dalam kode adalah penambahan beberapa flag opsional pada metode gradient descent stochastic Network.SGD.Bendera ini memungkinkan untuk melacak biaya dan akurasi pada training_data atau evaluation_data, yang dapat ditransmisikan ke Network.SGD. Sebelumnya di bab ini, kami sering menggunakan flag-flag ini, tetapi izinkan saya memberi contoh penggunaannya, hanya sebagai pengingat:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True) 

Kami menetapkan evaluation_data melalui validation_data. Namun, kami dapat melacak kinerja pada test_data dan kumpulan data lainnya. Kami juga memiliki empat flag yang menentukan kebutuhan untuk melacak biaya dan keakuratan baik pada evaluation_data dan training_data. Bendera ini disetel ke False secara default, namun mereka disertakan di sini untuk melacak efektivitas Jaringan. Selain itu, metode Network.SGD dari network2.py mengembalikan tupel empat elemen yang mewakili hasil pelacakan. Anda bisa menggunakannya seperti ini:

 >>> evaluation_cost, evaluation_accuracy, ... training_cost, training_accuracy = net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True) 

Jadi, misalnya, evaluation_cost akan menjadi daftar 30 elemen yang berisi biaya perkiraan data pada akhir setiap era. Informasi tersebut sangat berguna untuk memahami perilaku jaringan saraf. Informasi tersebut sangat berguna untuk memahami perilaku jaringan. Misalnya, dapat digunakan untuk menggambar grafik pembelajaran jaringan dari waktu ke waktu. Begitulah cara saya membuat semua grafik dari bab ini. Namun, jika salah satu flag tidak diatur, elemen tuple yang sesuai akan menjadi daftar kosong.

Tambahan kode lain termasuk metode Network.save, yang menyimpan objek Network ke disk, dan fungsi memuatnya ke dalam memori. Menyimpan dan memuat dilakukan melalui JSON, bukan modul acar Python atau cPickle, yang biasanya digunakan untuk menyimpan ke disk dan memuat dalam python. Menggunakan JSON membutuhkan lebih banyak kode daripada yang diperlukan untuk acar atau cPickle. Untuk memahami mengapa saya memilih JSON, bayangkan bahwa di beberapa titik di masa depan kami memutuskan untuk mengubah kelas Jaringan kami sehingga ada lebih dari neuron sigmoid. Untuk menerapkan perubahan ini, kami kemungkinan besar akan mengubah atribut yang didefinisikan dalam metode Network .__ init__. Dan jika kita hanya menggunakan acar untuk menghemat, fungsi beban kita tidak akan berfungsi. Menggunakan JSON dengan serialisasi eksplisit membuatnya mudah bagi kami untuk menjaminbahwa versi yang lebih lama dari objek Jaringan dapat diunduh.

Ada banyak perubahan kecil dalam kode, tetapi ini hanyalah variasi kecil dari network.py. Hasil akhirnya adalah perpanjangan dari program kami dari 74 baris ke program yang jauh lebih fungsional dari 152 baris.

Tantangan

• Ubah kode di bawah ini dengan memperkenalkan regularisasi L1, dan gunakan untuk mengklasifikasikan digit MNIST oleh jaringan dengan 30 neuron tersembunyi. Dapatkah Anda memilih parameter regularisasi yang memungkinkan Anda untuk meningkatkan hasil dibandingkan dengan jaringan tanpa regularisasi?
• Network.cost_derivative method network.py. . ? , ? network2.py Network.cost_derivative, CrossEntropyCost.delta. ?