🤞 💆🏽 👉🏾 Menghapus kebisingan frekuensi tinggi dari sinyal sensor getaran selama diagnostik getaran bantalan 🥀 👨‍🎤 👨🏼‍🎓

Pendahuluan

Salah satu tugas paling mendesak dari pemrosesan sinyal digital adalah tugas membersihkan sinyal dari kebisingan. Setiap sinyal praktis tidak hanya berisi informasi yang bermanfaat, tetapi juga jejak beberapa efek interferensi atau kebisingan yang tidak ada. Selain itu, selama diagnostik getaran, sinyal dari sensor getaran memiliki spektrum frekuensi non-stasioner, yang memperumit tugas penyaringan.

Ada banyak cara untuk menghilangkan noise frekuensi tinggi dari suatu sinyal. Misalnya, perpustakaan Scipy berisi filter berdasarkan berbagai metode penyaringan: Kalman; menghaluskan sinyal dengan rata-rata sepanjang sumbu waktu, dan lainnya.

Namun, keuntungan dari metode transformasi wavelet diskrit (DWT) adalah berbagai bentuk wavelet. Anda dapat memilih wavelet, yang akan memiliki karakteristik bentuk dari fenomena yang diharapkan. Misalnya, Anda dapat memilih sinyal dalam rentang frekuensi tertentu, yang bentuknya bertanggung jawab atas tampilan cacat.

Tujuan publikasi ini adalah untuk menganalisis metode penyaringan sinyal sensor getaran menggunakan konversi sinyal DWT, filter Kalman dan metode moving average.

Sumber data untuk analisis

Dalam publikasi, pengoperasian filter berdasarkan berbagai metode penyaringan akan dianalisis menggunakan set data NASA . Data diperoleh pada platform eksperimental PRONOSTIA:

Kit ini berisi data tentang sinyal sensor getaran untuk keausan berbagai jenis bantalan. Tujuan folder dengan file sinyal diberikan dalam tabel :

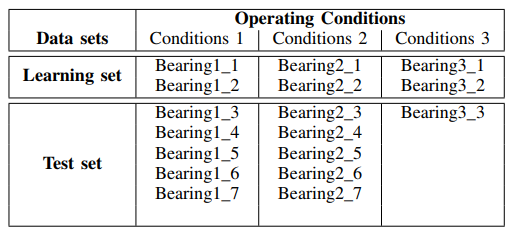
Pemantauan kondisi bantalan disediakan oleh sinyal sensor getaran (akselerometer horizontal dan vertikal), gaya dan suhu.

Sinyal diterima untuk tiga muatan berbeda:

Kondisi kerja pertama: 1800 rpm dan 4000 N;
Kondisi kerja kedua: 1650 rpm dan 4200 N;
Kondisi operasi ketiga: 1500 rpm dan 5000 N.

Untuk kondisi ini, menggunakan konversi sinyal wavelet kontinu, kami membuat skalogram daya spektro untuk data dari set tes - satu file (untuk satu jenis bantalan) dari folder: ['Test_set / Bearing1_3 / acc_00001.csv', 'Test_set / Bearing2_3 / acc_00001. csv ',' Test_set / Bearing3_3 / acc_00001.csv '] (lihat tabel 1).

Daftar Scaleogram

import scaleogram as scg import pandas as pd from pylab import * import pywt filename_n = ['Test_set/Bearing1_3/acc_00001.csv', 'Test_set/Bearing2_3/acc_00001.csv', 'Test_set/Bearing3_3/acc_00001.csv'] for filename in filename_n: df = pd.read_csv(filename, header=None) signal = df[4].values wavelet = 'cmor1-0.5' ax = scg.cws(signal, scales=arange(1, 40), wavelet=wavelet, figsize=(8, 4), cmap="jet", cbar=None, ylabel=' ', xlabel=" ", yscale="log", title='-  %s \n( )'%filename) show()

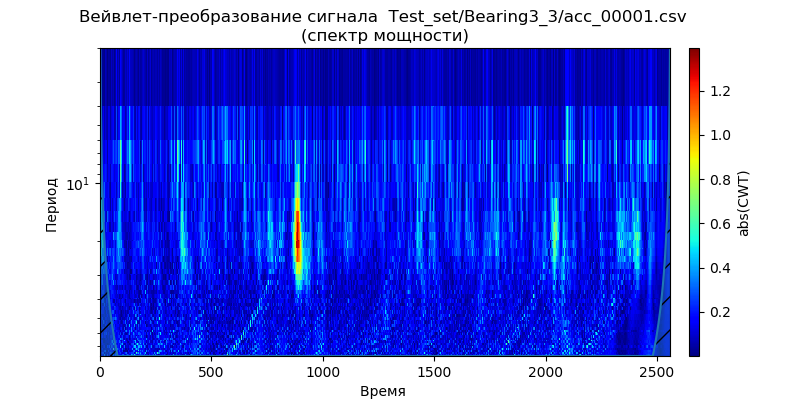
Ini mengikuti dari skala yang diberikan bahwa momen peningkatan kekuatan spektrum muncul lebih awal dalam waktu dan menunjukkan frekuensi untuk kondisi operasi: 1650 rpm dan 4200 N, yang menunjukkan degradasi dipercepat bantalan dalam pita frekuensi ini untuk gaya berkurang. Kami akan menggunakan sinyal ini ('Test_set / Bearing2_3 / acc_00001.csv') untuk menganalisis metode penghilangan derau.

Dekonstruksi Sinyal Menggunakan DWT

Dalam publikasi, kami melihat bagaimana bank filter diimplementasikan pada DWT yang dapat mendekonstruksi sinyal ke dalam subbands frekuensinya. Koefisien perkiraan (cA) mewakili bagian frekuensi rendah dari sinyal (filter rata-rata). Koefisien Detail (cD) mewakili bagian frekuensi tinggi dari sinyal. Selanjutnya, kita akan memeriksa bagaimana DWT dapat digunakan untuk mendekonstruksi sinyal ke dalam subbands frekuensinya dan mengembalikan sinyal aslinya.

Ada dua cara untuk memecahkan masalah dekonstruksi sinyal menggunakan alat PyWavelets:

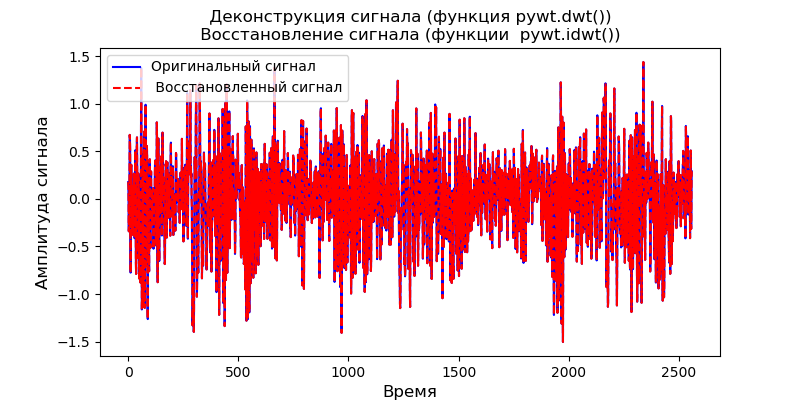
Cara pertama adalah menerapkan pywt.dwt () pada sinyal untuk mengekstraksi perkiraan dan koefisien detail (cA1, cD1). Kemudian, untuk mengembalikan sinyal, kita akan menggunakan pywt.idwt ():

Daftar

 import pywt from scipy import * import pandas as pd from pylab import * filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values (cA1, cD1) = pywt .dwt (signal, 'db2', 'smooth') r_signal = pywt.idwt (cA1, cD1, 'db2', 'smooth') fig, ax =subplots(figsize=(8,4)) ax.plot(signal, 'b',label=' ') ax.plot(r_signal, 'r', label='  ', linestyle='--') ax.legend(loc='upper left') ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) ax.set_title('   ( pywt.dwt()) \n   ( pywt.idwt()) ') show()

Cara kedua untuk menerapkan fungsi pywt.wavedec () pada sinyal adalah mengembalikan semua perkiraan dan koefisien detail ke level tertentu. Fungsi ini mengambil sinyal dan level input sebagai input dan mengembalikan satu set koefisien perkiraan (level ke-n) dan n set koefisien detail (dari level 1 ke level ke-ke-1). Untuk dekonstruksi, terapkan pywt.waverec ():

Daftar

 import pywt import pandas as pd from pylab import * filename = 'Test_set/Bearing3_3/acc_00026.csv' df = pd.read_csv(filename, header=None) signal = df[4].values coeffs = pywt.wavedec(signal, 'db2', level=8) r_signal = pywt.waverec(coeffs, 'db2') fig, ax = plt.subplots(figsize=(8,4)) ax.plot(signal, 'b',label=' ') ax.plot(r_signal, 'r ',label= ' ', linestyle='--') ax.legend(loc='upper left') ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) ax.set_title('    - level.\n   ( pywt.wavedec()) ') show()

Cara kedua untuk mendekonstruksi dan mengembalikan sinyal lebih mudah, ini memungkinkan Anda untuk segera mengatur tingkat dekonstruksi yang diinginkan.

Menghilangkan noise frekuensi tinggi dengan menghilangkan beberapa koefisien detail selama dekonstruksi sinyal

Kami akan mengembalikan sinyal dengan menghapus beberapa koefisien detail. Karena koefisien detail mewakili bagian frekuensi tinggi dari sinyal, kami cukup memfilter bagian spektrum frekuensi ini. Jika ada noise frekuensi tinggi dalam sinyal, ini adalah salah satu cara untuk memfilternya.

Di pustaka PyWavelets, ini bisa dilakukan menggunakan fungsi pemrosesan threshold pywt.threshol ():

pywt.threshold (data, nilai, mode = 'soft', pengganti = 0) ¶
data: seperti array_
Data numerik.
nilai: skalar
Nilai ambang batas.
mode: {'soft', 'hard', 'garrote', 'Greater', 'less'}
Menentukan jenis ambang yang akan diterapkan pada input. Standarnya adalah 'lunak'.
pengganti: float, opsional
Nilai pergantian (standar: 0).
output: array
Array ambang batas.

Penerapan fungsi pemrosesan ambang untuk nilai ambang yang diberikan sebaiknya dipertimbangkan dengan menggunakan contoh berikut:

 >>>> from scipy import* >>> import pywt >>> data =linspace(1, 4, 7) >>> data array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'soft') array([0. , 0. , 0. , 0.5, 1. , 1.5, 2. ]) >>> pywt.threshold(data, 2, 'hard') array([0. , 0. , 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'garrote') array([0. , 0. , 0., 0.9,1.66666667, 2.35714286, 3.])

Kami memplot grafik fungsi ambang menggunakan daftar berikut:

Daftar

 from scipy import* from pylab import* import pywt s = linspace(-4, 4, 1000) s_soft = pywt.threshold(s, value=0.5, mode='soft') s_hard = pywt.threshold(s, value=0.5, mode='hard') s_garrote = pywt.threshold(s, value=0.5, mode='garrote') figsize=(10, 4) plot(s, s_soft) plot(s, s_hard) plot(s, s_garrote) legend(['soft (0.5)', 'hard (0.5)', 'non-neg. garrote (0.5)']) xlabel('   ') ylabel('  ') show()

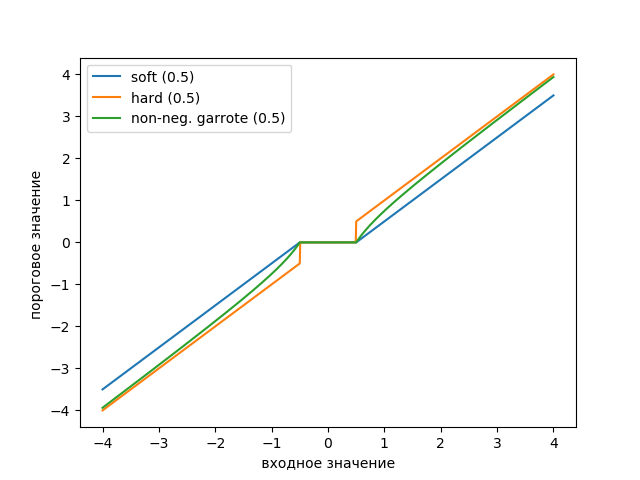
Grafik menunjukkan bahwa ambang batas Garott non-negatif adalah perantara antara ambang lunak dan keras. Sepasang ambang batas diperlukan untuk menentukan lebar wilayah transisi.

Pengaruh fungsi ambang pada karakteristik filter

Sebagai berikut dari grafik di atas, hanya dua fungsi ambang 'lunak' dan 'garrote' yang cocok untuk kami, untuk mempelajari pengaruhnya terhadap karakteristik filter, kami menuliskan daftar:

Daftar

 import pandas as pd from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values v='bior4.4' thres=['soft' ,'garrote'] for w in thres: def lowpassfilter(signal, thresh, wavelet=v): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode=w ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal, 0.4) ax.plot(rec, 'r', label='DWT  ', linewidth=2) ax.legend() ax.set_title('      :%s\n   :%s'%(v,w), fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()

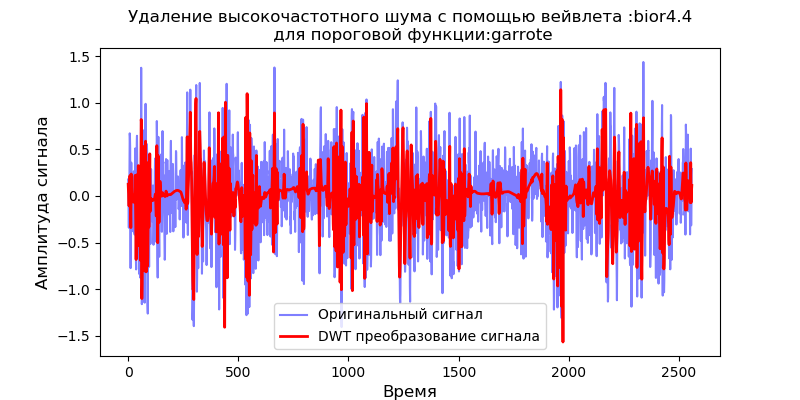
Sebagai berikut dari grafik, fungsi lunak memberikan perataan yang lebih baik daripada fungsi 'garrote', jadi kami akan menggunakan fungsi lunak di masa mendatang.

Pengaruh ambang detail pada karakteristik filter

Untuk jenis filter yang dipertimbangkan, ambang batas untuk mengubah koefisien detail adalah karakteristik penting, oleh karena itu, kami mempelajari efeknya menggunakan daftar berikut:

Daftar

 import pandas as pd from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values v='bior4.4' thres=[0.1,0.4,0.6] for w in thres: def lowpassfilter(signal, thresh, wavelet=v): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal,w) ax.plot(rec, 'r', label='DWT  ', linewidth=2) ax.legend() ax.set_title('      :%s\n    %s'%(v,w), fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()

Sebagai berikut dari grafik yang diperoleh, tingkat ambang detail mempengaruhi skala bagian yang disaring. Dengan peningkatan ambang, wavelet mengurangi kebisingan dari tingkat yang terus meningkat sampai terjadi pembesaran skala detail yang berlebihan dan transformasi mulai mengubah bentuk sinyal asli.Untuk sinyal kami, ambang batas tidak boleh lebih tinggi dari 0,63.

Efek wavelet pada karakteristik filter

Pustaka PyWavelets memiliki jumlah wavelet yang cukup untuk konversi DWT, yang dapat diperoleh seperti ini:

 >>> import pywt >>> print(pywt.wavelist(kind= 'discrete')) ['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20']

Pengaruh wavelet pada karakteristik filter tergantung pada fungsi primitifnya. Untuk menunjukkan ketergantungan ini, kami memilih dua wavelet dari keluarga Dobeshi - db1 dan db38, dan mempertimbangkan keluarga-keluarga ini:

Daftar

 import pywt from pylab import* db_wavelets = ['db1', 'db38'] fig, axarr = subplots(ncols=2, nrows=5, figsize=(14,8)) fig.suptitle('  : db1,db38', fontsize=14) for col_no, waveletname in enumerate(db_wavelets): wavelet = pywt.Wavelet(waveletname) no_moments = wavelet.vanishing_moments_psi family_name = wavelet.family_name for row_no, level in enumerate(range(1,6)): wavelet_function, scaling_function, x_values = wavelet.wavefun(level = level) axarr[row_no, col_no].set_title("{} : {}.   : {}. :: {} ".format( waveletname, level, no_moments, len(x_values)), loc='left') axarr[row_no, col_no].plot(x_values, wavelet_function, 'b--') axarr[row_no, col_no].set_yticks([]) axarr[row_no, col_no].set_yticklabels([]) tight_layout() subplots_adjust(top=0.9) show()

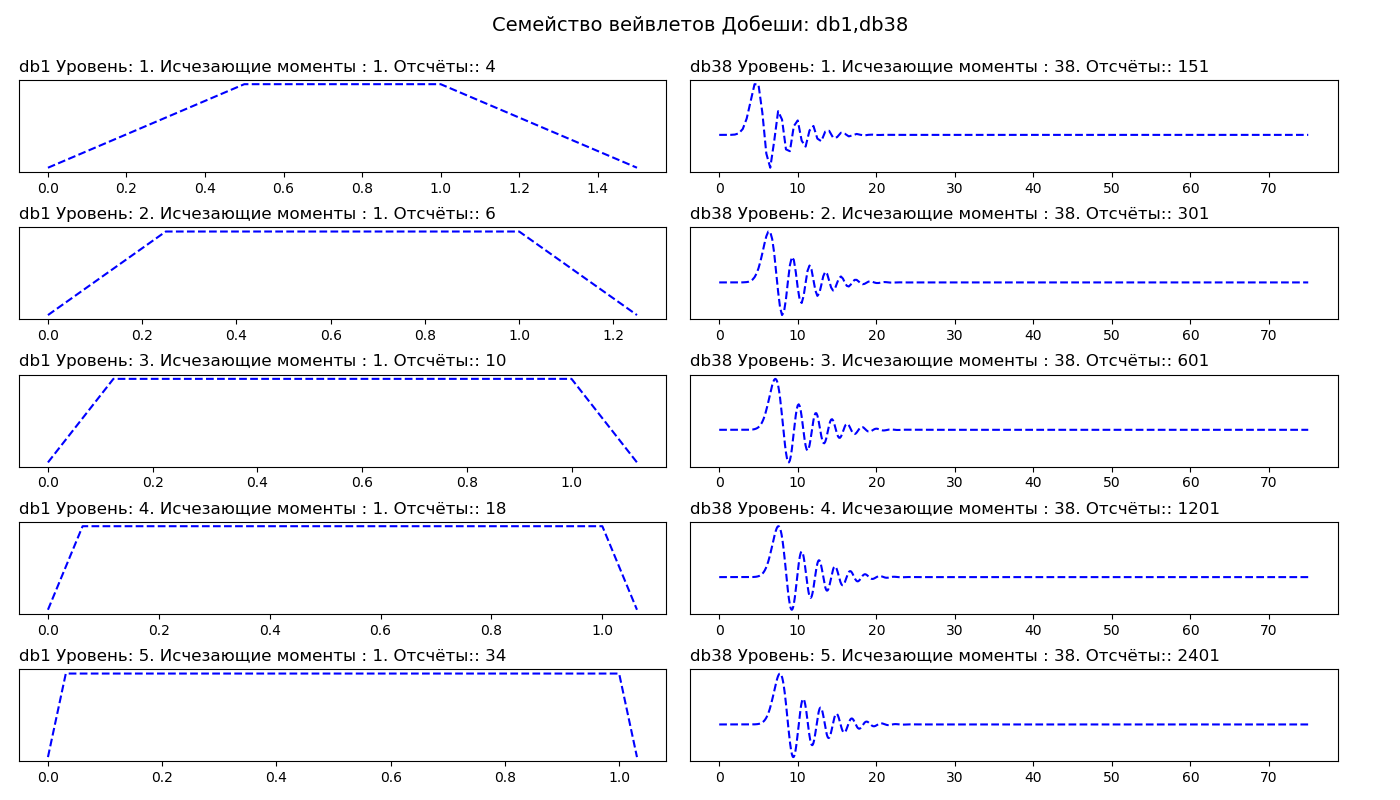
Pada kolom pertama kita melihat wavelet Daubeshi dari orde pertama (db1), di kolom kedua dari orde tiga puluh delapan (db38). Dengan demikian, db1 memiliki satu momen kepunahan, dan db38 memiliki 38 saat kepunahan. Jumlah momen penghilangan terkait dengan urutan aproksimasi dan kelancaran wavelet. Jika wavelet memiliki P poin menghilang, ia dapat mendekati polinomial derajat P - 1.

Wavelet yang lebih halus menghasilkan aproksimasi sinyal yang lebih halus, dan sebaliknya - wavelet "pendek" lebih baik melacak puncak fungsi yang didekati. Saat memilih wavelet, kita juga dapat menunjukkan tingkat dekomposisi yang seharusnya. Secara default, PyWavelets memilih tingkat dekomposisi maksimum yang mungkin untuk sinyal input. Level dekomposisi maksimum tergantung pada panjang sinyal input dan wavelet:

Daftar

 import pandas as pd import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) data = df[4].values w=['db1', 'db38'] for v in w: n_level=pywt.dwt_max_level(len(data),v) print('  %s   : %s ' %(v,n_level))

Untuk db1 wavelet, level dekomposisi maksimum: 11
Untuk db38 wavelet, level dekomposisi maksimum: 5

Untuk nilai yang diperoleh dari level maksimum dekomposisi wavelet, kami mempertimbangkan pengoperasian filter untuk menghilangkan noise frekuensi tinggi:

Daftar

 import pandas as pd import scaleogram as scg from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values discrete_wavelets =[('db38', 5),('db1',11)] for v in discrete_wavelets: def lowpassfilter(signal, thresh = 0.63, wavelet=v[0]): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal wavelet = pywt.DiscreteContinuousWavelet(v[0]) phi, psi, x = wavelet.wavefun(level=v[1]) fig, ax = subplots(figsize=(8,4)) ax.set_title("   : %s,level=%s"%(v[0],v[1]), fontsize=12) ax.plot(x,phi,linewidth=2) fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label='   ') rec = lowpassfilter(signal, 0.4) ax.plot(rec, 'r', label='DWT  ', linewidth=2) ax.legend() ax.set_title('   \n   :%s,level=%s'%(v[0],v[1]),fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) wavelet = 'cmor1-0.5' ax = ax = scg.cws(rec, scales=arange(1,128), wavelet=wavelet,figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT  \n(   DWT  )') show()

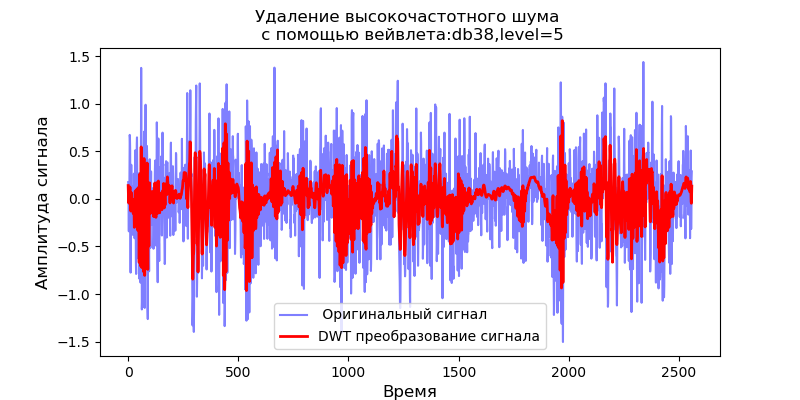
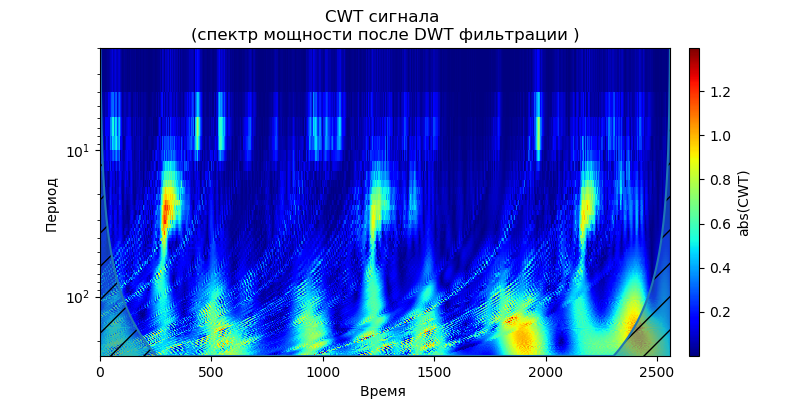
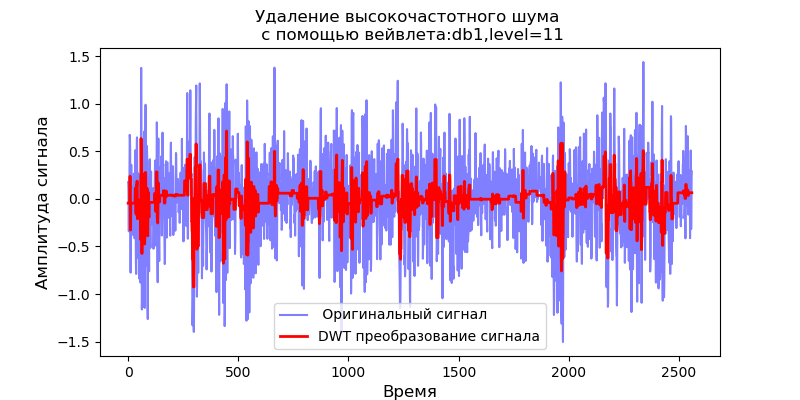
Ini mengikuti dari skalogram yang diberikan sinyal pada output filter yang, untuk wavelet db38, kekuatan puncak spektrum diikuti oleh daerah terlokalisasi, untuk wavelet db1, wilayah ini menghilang. Perlu dicatat bahwa, misalnya, wavelet db38 dapat mendekati sinyal polinomial derajat 37. Ini memperluas klasifikasi sinyal, misalnya, untuk mengidentifikasi kerusakan peralatan sesuai dengan sinyal sensor getaran.

Karena sinyal setelah filter dengan wavelet Daubechies membentuk deret waktu menggunakan koefisien aproksimasi dan dekomposisi sebagai karakteristik dari deret tersebut, seseorang dapat menentukan tingkat kedekatan deret tersebut, yang sangat menyederhanakan pencarian dan klasifikasi mereka.

Filter Kalman untuk menghilangkan noise frekuensi tinggi

Filter Kalman banyak digunakan untuk menyaring kebisingan di berbagai sistem dinamis. Pertimbangkan sistem dinamis dengan vektor keadaan x.

$x = F \ cdot x + w (Q)$

di mana F adalah matriks transisi
w (Q) adalah proses acak (noise) dengan nol harapan matematika dan matriks kovarians Q.

Kami akan mengamati keadaan transisi sistem dengan kesalahan pengukuran yang diketahui pada setiap saat. Menghapus kebisingan menggunakan metode Kalman terdiri dari dua langkah - ekstrapolasi dan koreksi, sepertinya ini.

Atur parameter sistem:

Q-matrix dari kovarians kebisingan (process covariance noise).
H adalah matriks observasi (pengukuran).
R - kovarians noise pengamatan (pengukuran kovarians noise).
P = Q adalah nilai awal dari matriks kovarians untuk vektor keadaan.
z (t) adalah keadaan sistem yang diamati.
x = z (0) adalah nilai awal dari penilaian kondisi sistem.

Untuk setiap pengamatan z, kami akan menghitung status yang disaring x
dan untuk ini kami melakukan langkah-langkah berikut.

• langkah 1: ekstrapolasi
1. ekstrapolasi (prediksi) dari keadaan sistem

$x = F \ cdot x$
2. menghitung matriks kovarians untuk vektor keadaan terekstrapolasi

$F = F \ cdot P \ cdot F ^ {T} + Q$

• langkah 2: koreksi
1. menghitung vektor kesalahan, penyimpangan pengamatan dari keadaan yang diharapkan

$y = z-H \ cdot x$
2. menghitung matriks kovarians untuk vektor deviasi (vektor kesalahan)

$S = H \ cdot P \ cdot H ^ {T} + R$
3. menghitung keuntungan Kalman

$K = P \ cdot H \ cdot H ^ {T} \ cdot S ^ {- 1}$
4. koreksi estimasi vektor negara

$x = x + K \ cdot y$
5. kami mengoreksi matriks kovarians untuk memperkirakan vektor status sistem

$P = (I-K \ cdot H) \ cdot P$

Daftar untuk implementasi algoritma

 from scipy import* from pylab import* import pandas as pd def kalman_filter( z, F = eye(2), #     (transitionMatrix) Q = eye(2)*3e-3, #   (processNoiseCov) H = eye(2), #   (measurement) R = eye(2)*3e-1 #    (measurementNoiseCov) ): n = z.shape[0] #   #m = z.shape[1] #   x = z[0,:].transpose() #      P = Q #       r = [ x ] #  for i in range(1,n): # : x = F.dot( x ) #  ()   P = F.dot(P).dot( F.transpose() ) + Q #       # : y = z[i] - H.dot(x) #  ,      ()  S = H.dot(P).dot(H.transpose()) + R #      ( ) K = P.dot(H.transpose()).dot(linalg.inv(S)) #     x = x + K.dot(y) #     P = ( eye(z.shape[1]) - K.dot(H) ).dot(P) #       r.append( x.transpose()) return array(r) filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values N= signal .shape[0] #   # 2 dimensions y0 =linspace(0.0,2500.0,N) y1 =signal d = array(list(zip(y0,y1))) dn = dr = kalman_filter(dn) fig, ax = subplots(figsize=(8,4)) ax.plot( d[:,0], d[:,1],'b', label=' ' ) ax.plot( r[:,0], r[:,1],'r', label='kalman' ) ax.legend(loc='upper left') ax.set_title('       \n (  )', fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()

Untuk model dinamis yang diberikan, Anda dapat menggunakan pustaka pyKalman:

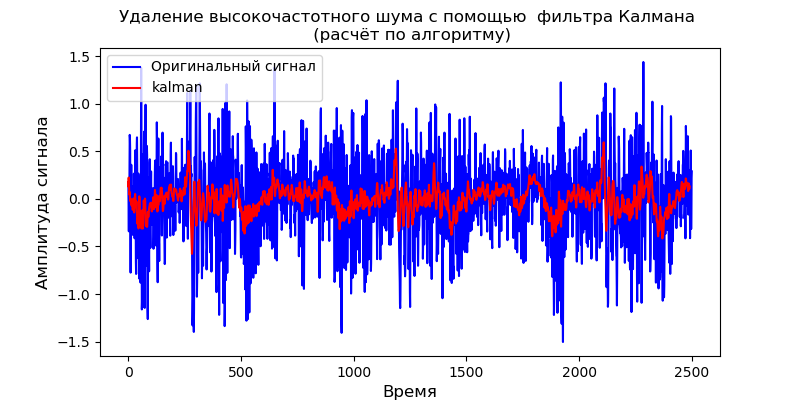
Daftar

 from pykalman import KalmanFilter import pandas as pd from pylab import * import scaleogram as scg filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values measurements =signal kf = KalmanFilter(transition_matrices=[1] ,# A      t  t+1 observation_matrices=[1],# C   initial_state_mean=measurements[0],#   initial_state_covariance=[1],#    observation_covariance=[1],# R    transition_covariance= 0.01) # Q     state_means, state_covariances = kf.filter(measurements)# ,   state_means=[w[0] for w in state_means] state_std = sqrt(state_covariances[:,0]) fig, ax = subplots(figsize=(8,4)) ax.plot(measurements ,'b', label=' ') ax.plot(state_means ,'r', label='kalman- ') ax.legend() ax.set_title('      \n ( pyKalman)', fontsize=14) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) wavelet = 'cmor1-0.5' ax = ax = scg.cws(signal, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4),cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT    \n( )') ax = ax = scg.cws(state_means, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT     \n(  )') show()

Sumur filter Kalman menghilangkan noise frekuensi tinggi, namun, itu tidak memungkinkan mengubah bentuk sinyal output.

Metode rata-rata bergerak

Dalam menentukan arah perubahan utama dalam urutan berosilasi kuat, masalah timbul karena memuluskannya menggunakan metode rata-rata bergerak. Ini mungkin pembacaan sensor level bahan bakar di dalam mobil atau, seperti dalam kasus kami, data sensor frekuensi tinggi mengenai degradasi dipercepat bantalan. Masalahnya dapat dianggap sebagai pemulihan beberapa urutan r di mana kebisingan ditumpangkan.

Simple Moving Average untuk pendek - SMA (Simple Moving Average). Untuk menghitung nilai filter saat ini

$r_ {i}$ kita hanya rata-rata elemen n sebelumnya dari urutan, sehingga filter mulai bekerja dengan elemen urutan n.

$r_ {i} = \ frac {1} {n} \ cdot \ sum_ {j = 1} ^ {n} y _ {(i-j)}; i> n$

Daftar

 <source lang="python">from scipy import * import pandas as pd from pylab import * import pywt import scaleogram as scg def get_ave_values(xvalues, yvalues, n = 6): signal_length = len(xvalues) if signal_length % n == 0: padding_length = 0 else: padding_length = n - signal_length//n % n xarr = array(xvalues) yarr = array(yvalues) xarr.resize(signal_length//n, n) yarr.resize(signal_length//n, n) xarr_reshaped = xarr.reshape((-1,n)) yarr_reshaped = yarr.reshape((-1,n)) x_ave = xarr_reshaped[:,0] y_ave = nanmean(yarr_reshaped, axis=1) return x_ave, y_ave def plot_signal_plus_average(time, signal, average_over = 5): fig, ax = subplots(figsize=(8, 4)) time_ave, signal_ave = get_ave_values(time, signal, average_over) ax.plot(time_ave, signal_ave,"b", label = '   (n={})'.format(5)) ax.set_xlim([time[0], time[-1]]) ax.set_ylabel(' ', fontsize=12) ax.set_title('     SMA', fontsize=14) ax.set_xlabel('', fontsize=12) ax.legend() return signal_ave filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) df_nino = df[4].values N = df_nino.shape[0] time = arange(0, N) signal = df_nino signal_ave=plot_signal_plus_average(time, signal) wavelet = 'cmor1-0.5' ax = ax = scg.cws(signal, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4),cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT  %s \n(     )'%filename) ax = ax = scg.cws(signal_ave, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT  %s \n(    )'%filename) show()

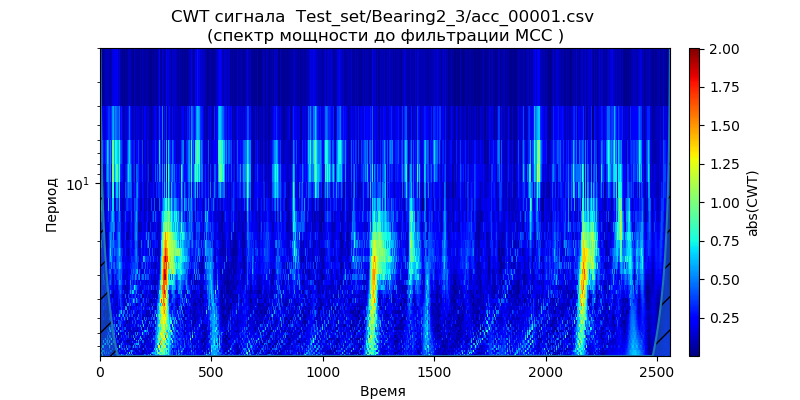
Sebagai berikut dari skalogram, metode SMA membersihkan sinyal dari noise frekuensi tinggi, dan
seperti yang disebutkan di atas digunakan untuk menghaluskan.

Kesimpulan:

Menggunakan modul scaleogram, skalogram wavelet CWT dari tiga sinyal sensor getaran uji diperoleh untuk kondisi pengujian yang berbeda untuk bantalan dari jenis yang sama. Menurut data skalogram, dipilih sinyal dengan tanda-tanda degradasi lambat yang dinyatakan dengan jelas. Sinyal ini digunakan untuk menunjukkan operasi filter dalam semua contoh yang diberikan.
Metode perpustakaan PyWavelets untuk dekonstruksi DWT dan pemulihan sinyal sensor getaran menggunakan modul pywt.dwt (), pywt.idwt () dan modul pywt.wavedec () untuk level wavelet yang diberikan dipertimbangkan.
Contoh-contoh menunjukkan fitur aplikasi modul pywt.threshol () untuk memfilter koefisien penyempitan DWT, yang bertanggung jawab untuk bagian spektrum frekuensi tinggi menggunakan fungsi ambang untuk nilai ambang tertentu.
Efek dari gelombang DWT antiderivatif pada bentuk sinyal yang dibersihkan dari kebisingan dipertimbangkan.
Model filter Kalman untuk media dinamis diperoleh, model diuji pada sinyal uji sensor getaran. Plot penghilangan derau sama dengan yang diperoleh menggunakan modul pyKalman. Sifat grafik bertepatan dengan skalogram.
.

Menghapus kebisingan frekuensi tinggi dari sinyal sensor getaran selama diagnostik getaran bantalan

Pendahuluan

Sumber data untuk analisis

Dekonstruksi Sinyal Menggunakan DWT

Menghilangkan noise frekuensi tinggi dengan menghilangkan beberapa koefisien detail selama dekonstruksi sinyal

Pengaruh fungsi ambang pada karakteristik filter

Pengaruh ambang detail pada karakteristik filter

Efek wavelet pada karakteristik filter

Filter Kalman untuk menghilangkan noise frekuensi tinggi

Metode rata-rata bergerak

Kesimpulan:

More articles: