
Ilmu data menjadi bagian integral dari setiap kegiatan pemasaran, dan buku ini adalah potret hidup dari transformasi digital dalam pemasaran. Analisis data dan algoritma pintar mengotomatiskan tugas pemasaran yang menghabiskan waktu. Proses pengambilan keputusan menjadi tidak hanya lebih sempurna, tetapi juga lebih cepat, yang sangat penting dalam lingkungan kompetitif yang terus meningkat.
“Buku ini adalah potret hidup dari transformasi digital dalam pemasaran. Ini menunjukkan bagaimana ilmu data menjadi bagian integral dari setiap kegiatan pemasaran. Ini menjelaskan secara terperinci bagaimana pendekatan yang didasarkan pada analisis data dan algoritma cerdas berkontribusi pada otomatisasi mendalam dari tugas pemasaran padat karya tradisional. Proses pengambilan keputusan menjadi tidak hanya lebih sempurna, tetapi juga lebih cepat, yang penting dalam lingkungan kompetitif kita yang terus meningkat. Buku ini harus dibaca oleh spesialis pemrosesan data dan spesialis pemasaran, dan lebih baik jika mereka membacanya bersama. " Andrey Sebrant, Direktur Pemasaran Strategis, Yandex.
Kutipan. 5.8.3. Model Faktor Tersembunyi
Dalam algoritme penyaringan bersama yang dibahas sejauh ini, sebagian besar perhitungan didasarkan pada elemen individual dari matriks peringkat. Metode berbasis kedekatan mengevaluasi peringkat yang hilang langsung dari nilai yang diketahui dalam matriks peringkat. Metode berbasis model menambahkan lapisan abstraksi di atas matriks peringkat, menciptakan model prediksi yang menangkap pola hubungan tertentu antara pengguna dan elemen, tetapi pelatihan model masih sangat tergantung pada sifat-sifat matriks peringkat. Akibatnya, teknik penyaringan kolaboratif ini biasanya menghadapi masalah berikut:
Matriks peringkat dapat berisi jutaan pengguna, jutaan elemen, dan miliaran peringkat yang diketahui, yang menciptakan masalah serius pada kompleksitas komputasi dan skalabilitas.
Matriks peringkat biasanya sangat jarang (dalam praktiknya, sekitar 99% peringkat mungkin hilang). Ini memengaruhi stabilitas komputasi dari algoritme rekomendasi dan menyebabkan perkiraan yang tidak dapat diandalkan ketika pengguna atau elemen tidak memiliki tetangga yang benar-benar mirip. Masalah ini sering diperburuk oleh fakta bahwa sebagian besar algoritma dasar berorientasi pada pengguna atau elemen, yang membatasi kemampuan mereka untuk merekam semua jenis persamaan dan hubungan yang tersedia dalam matriks peringkat.
Data dalam matriks peringkat biasanya sangat berkorelasi karena kesamaan antara pengguna dan elemen. Ini berarti bahwa sinyal yang tersedia dalam matriks peringkat tidak hanya jarang, tetapi juga redundan, yang berkontribusi pada eksaserbasi masalah skalabilitas.
Pertimbangan di atas menunjukkan bahwa matriks peringkat asli mungkin bukan representasi sinyal yang paling optimal, dan representasi alternatif lain yang lebih cocok untuk pemfilteran bersama harus dipertimbangkan. Untuk menjelajahi ide ini, mari kita kembali ke titik awal dan berpikir sedikit tentang sifat dari layanan rekomendasi. Bahkan, layanan rekomendasi dapat dianggap sebagai algoritme yang memprediksi peringkat berdasarkan pada beberapa ukuran kesamaan antara pengguna dan elemen:
Salah satu cara untuk menentukan ukuran kesamaan ini adalah dengan menggunakan pendekatan faktor tersembunyi dan memetakan pengguna dan elemen ke titik dalam beberapa ruang dimensi k sehingga setiap pengguna dan setiap elemen diwakili oleh vektor dimensi k:
Vektor harus dikonstruksi sedemikian sehingga dimensi yang sesuai p dan q dapat dibandingkan satu sama lain. Dengan kata lain, setiap dimensi dapat dianggap sebagai tanda atau konsep, yaitu, puj adalah ukuran kedekatan pengguna u dan konsep j, dan qij, masing-masing, adalah ukuran elemen i dan konsep j. Dalam praktiknya, dimensi ini sering ditafsirkan sebagai genre, gaya, dan atribut lainnya yang berlaku secara simultan untuk pengguna dan elemen. Kesamaan antara pengguna dan elemen dan, dengan demikian, peringkat dapat didefinisikan sebagai produk dari vektor yang sesuai:

Karena setiap peringkat dapat didekomposisi menjadi produk dari dua vektor yang termasuk dalam ruang konsep yang tidak secara langsung diamati dalam matriks peringkat asli, p dan q disebut faktor tersembunyi. Keberhasilan pendekatan abstrak ini, tentu saja, sepenuhnya tergantung pada bagaimana faktor-faktor tersembunyi ditentukan dan dibangun. Untuk menjawab pertanyaan ini, kami mencatat bahwa ekspresi 5.92 dapat ditulis ulang dalam bentuk matriks sebagai berikut:
di mana P adalah matriks n × k yang dirakit dari vektor p, dan Q adalah matriks mxk yang dirakit dari vektor q, seperti yang ditunjukkan pada Gambar. 5.13. Tujuan utama dari sistem pemfilteran gabungan biasanya untuk meminimalkan kesalahan prediksi peringkat, yang memungkinkan Anda untuk secara langsung menentukan masalah pengoptimalan sehubungan dengan matriks faktor tersembunyi:
Dengan asumsi bahwa jumlah dimensi tersembunyi k adalah tetap dan k ≤ n dan k ≤ m, masalah optimisasi 5.94 berkurang menjadi masalah perkiraan peringkat rendah, yang kami bahas pada Bab 2. Untuk mendemonstrasikan pendekatan terhadap solusi, mari kita asumsikan sejenak bahwa matriks peringkat telah selesai. Dalam hal ini, masalah optimisasi memiliki solusi analitis dalam hal Singular Value Decomposition (SVD) dari matriks peringkat. Secara khusus, menggunakan algoritma SVD standar, matriks dapat didekomposisi menjadi produk dari tiga matriks:
di mana U adalah matriks n × n yang dinormalisasi oleh kolom, Σ adalah matriks diagonal n × m, dan V adalah matriks mx m yang di-orthonormalisasi oleh kolom. Solusi optimal untuk masalah 5.94 dapat diperoleh dalam hal faktor-faktor ini, terpotong ke k dimensi paling signifikan:
Akibatnya, faktor tersembunyi yang optimal dalam hal akurasi prediksi dapat diperoleh dengan dekomposisi singular, seperti yang ditunjukkan di bawah ini:
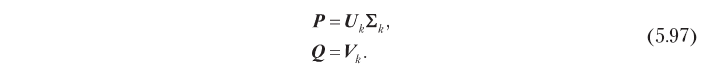
Model faktor tersembunyi berbasis SVD ini membantu memecahkan masalah pemfilteran bersama yang dijelaskan di awal bagian ini. Pertama, ia menggantikan matriks rating n × m yang besar dengan matriks faktor n × k dan m × k, yang biasanya jauh lebih kecil, karena dalam praktiknya jumlah optimal dimensi tersembunyi k sering kecil. Sebagai contoh, ada kasus di mana matriks penilaian dengan 500.000 pengguna dan 17.000 elemen mampu didekati dengan cukup baik menggunakan 40 pengukuran [Funk, 2016]. Lebih lanjut, SVD menghilangkan korelasi dalam matriks peringkat: matriks faktor laten yang didefinisikan oleh 5.97 adalah ortonormal dalam kolom, yaitu dimensi tersembunyi tidak berkorelasi. Jika, yang biasanya benar dalam praktiknya, SVD juga memecahkan masalah kerapuhan, karena sinyal yang ada dalam matriks peringkat awal terkonsentrasi secara efektif (ingat bahwa kami memilih dimensi k dengan energi sinyal tertinggi), dan matriks faktor laten tidak jarang. Gambar 5.14 menggambarkan properti ini. Algoritme kedekatan berbasis pengguna (5.14, a) runtuh vektor peringkat jarang untuk elemen yang diberikan dan pengguna yang diberikan untuk mendapatkan skor peringkat. Model faktor tersembunyi (5.14, b), sebaliknya, memperkirakan peringkat dengan konvolusi dua vektor dimensi tereduksi dan dengan kepadatan energi yang lebih tinggi.

Pendekatan yang baru saja dideskripsikan terlihat seperti solusi yang koheren untuk masalah faktor tersembunyi, tetapi pada kenyataannya memiliki kelemahan serius karena asumsi bahwa matriks peringkat telah selesai. Jika matriks peringkat jarang, yang hampir selalu demikian, algoritma SVD standar tidak dapat diterapkan secara langsung, karena tidak dapat memproses elemen yang hilang (tidak ditentukan). Solusi paling sederhana dalam hal ini adalah mengisi peringkat yang hilang dengan beberapa nilai default, tetapi ini dapat menyebabkan bias serius dalam perkiraan. Selain itu, ini tidak efisien secara komputasi karena kompleksitas komputasi dari solusi seperti itu sama dengan kompleksitas SVD untuk matriks n × m penuh, sementara itu diinginkan untuk memiliki metode dengan kompleksitas yang proporsional dengan jumlah peringkat yang diketahui. Masalah-masalah ini dapat diatasi dengan menggunakan metode dekomposisi alternatif yang dijelaskan pada bagian berikut.
5.8.3.1. Dekomposisi tidak terbatas
Algoritma SVD standar adalah solusi analitis untuk masalah pendekatan peringkat rendah. Namun, masalah ini dapat dianggap sebagai masalah optimisasi, dan metode optimisasi universal juga dapat diterapkan. Salah satu pendekatan yang paling sederhana adalah dengan menggunakan metode gradient descent untuk memperbaiki nilai faktor tersembunyi secara iteratif. Titik awal adalah definisi fungsi biaya J sebagai kesalahan perkiraan residual:
Harap perhatikan bahwa saat ini kami tidak memaksakan pembatasan apa pun, seperti ortogonalitas, pada matriks faktor tersembunyi. Menghitung gradien fungsi biaya sehubungan dengan faktor-faktor tersembunyi, kami memperoleh hasil sebagai berikut:
di mana E adalah matriks kesalahan residual:
Algoritma gradient descent meminimalkan fungsi biaya dengan bergerak pada setiap langkah ke arah negatif gradien. Oleh karena itu, Anda dapat menemukan faktor tersembunyi yang meminimalkan kesalahan kuadrat dari prediksi peringkat dengan secara iteratif mengubah matriks P dan Q untuk bertemu, sesuai dengan ekspresi berikut:

di mana α adalah kecepatan belajar. Kerugian dari metode gradient descent adalah kebutuhan untuk menghitung seluruh matriks kesalahan residual dan secara bersamaan mengubah semua nilai faktor-faktor tersembunyi di setiap iterasi. Pendekatan alternatif, yang mungkin lebih cocok untuk matriks besar, adalah penurunan gradien stokastik [Funk, 2016]. Algoritma gradient descent stochastic menggunakan fakta bahwa kesalahan perkiraan total J adalah jumlah kesalahan untuk elemen individu dari matriks peringkat, oleh karena itu, gradien umum J dapat didekati dengan gradien pada satu titik data dan faktor-faktor tersembunyi dapat diubah berdasarkan elemen. Implementasi penuh dari ide ini ditunjukkan dalam algoritma 5.1.

Tahap pertama dari algoritma adalah inisialisasi matriks faktor tersembunyi. Pilihan nilai-nilai awal ini tidak terlalu penting, tetapi dalam kasus ini, distribusi yang seragam dari energi dari peringkat yang diketahui di antara faktor-faktor tersembunyi yang dihasilkan secara acak dipilih. Kemudian algoritma secara berurutan mengoptimalkan dimensi konsep. Untuk setiap pengukuran, ini berulang kali mengelilingi semua peringkat dalam set pelatihan, memprediksi setiap peringkat menggunakan nilai saat ini dari faktor-faktor tersembunyi, memperkirakan kesalahan dan mengoreksi nilai-nilai faktor sesuai dengan ekspresi 5.101. Optimalisasi pengukuran selesai ketika kondisi konvergensi terpenuhi, setelah itu algoritma melanjutkan ke pengukuran berikutnya.
Algoritma 5.1 membantu mengatasi keterbatasan metode SVD standar. Ini mengoptimalkan faktor tersembunyi dengan perulangan melalui titik data individual, dan dengan demikian menghindari masalah dengan peringkat yang hilang dan operasi aljabar dengan matriks raksasa. Pendekatan iteratif juga membuat penurunan gradien stokastik lebih nyaman untuk aplikasi praktis daripada penurunan gradien, yang memodifikasi seluruh matriks menggunakan ekspresi 5.101.
CONTOH 5.6
Faktanya, pendekatan yang didasarkan pada faktor-faktor tersembunyi adalah seluruh kelompok metode representasi pengajaran yang dapat mengidentifikasi pola-pola yang tersirat dalam matriks peringkat dan mewakilinya secara eksplisit dalam bentuk konsep. Terkadang konsep memiliki interpretasi yang sepenuhnya bermakna, terutama yang berenergi tinggi, meskipun ini tidak berarti bahwa semua konsep selalu memiliki makna yang bermakna. Misalnya, menerapkan algoritma dekomposisi matriks ke database peringkat film dapat membuat faktor yang kira-kira sesuai dengan dimensi psikografis, seperti melodrama, komedi, horor, dll. Mari kita ilustrasikan fenomena ini dengan contoh numerik kecil yang menggunakan matriks peringkat dari Tabel. 5.3:
Pertama, kurangi rata-rata global μ = 2.82 dari semua elemen untuk memusatkan matriks, dan kemudian jalankan algoritma 5.1 dengan k = 3 pengukuran tersembunyi dan tingkat pembelajaran α = 0,01 untuk mendapatkan dua matriks faktor berikut:

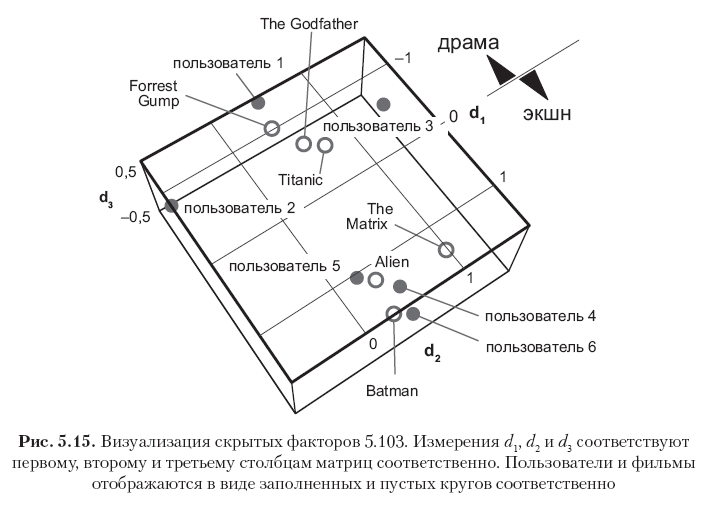
Setiap baris dalam matriks ini sesuai dengan pengguna atau film, dan semua vektor 12 baris ditunjukkan pada Gambar. 5.15. Harap dicatat bahwa elemen-elemen di kolom pertama (vektor konsep pertama) memiliki nilai terbesar, dan nilai-nilai di kolom berikutnya secara bertahap berkurang. Ini dijelaskan oleh fakta bahwa vektor konsep pertama menangkap energi sinyal sebanyak mungkin untuk menangkap menggunakan satu pengukuran, vektor konsep kedua hanya menangkap sebagian dari energi residual, dll. Lebih lanjut, perhatikan bahwa konsep pertama dapat secara semantik diartikan sebagai sumbu drama - film aksi, di mana arah positif sesuai dengan genre film aksi, dan negatif - ke genre drama. Peringkat dalam contoh ini sangat berkorelasi, sehingga dapat dilihat dengan jelas bahwa tiga pengguna pertama dan tiga film pertama memiliki nilai negatif besar dalam vektor konsep pertama (film drama dan pengguna yang menyukai film tersebut), sedangkan tiga pengguna terakhir dan tiga terakhir film memiliki makna positif yang luar biasa di kolom yang sama (film aksi dan pengguna yang menyukai genre ini). Dimensi kedua dalam kasus khusus ini berhubungan terutama dengan bias pengguna atau elemen, yang dapat diartikan sebagai atribut psikografis (kekritisan penilaian pengguna? Popularitas film?). Konsep lain dapat dianggap sebagai kebisingan.
Matriks faktor yang dihasilkan tidak sepenuhnya ortogonal dalam kolom, tetapi cenderung ortogonal, karena ini mengikuti dari optimalitas solusi SVD. Ini dapat dilihat dengan melihat produk-produk PTP dan QTQ, yang dekat dengan matriks diagonal:
Matriks 5.103 pada dasarnya adalah model prediksi yang dapat digunakan untuk mengevaluasi peringkat yang diketahui dan yang hilang. Perkiraan dapat diperoleh dengan mengalikan dua faktor dan menambahkan kembali rata-rata global:
Hasilnya secara akurat mereproduksi yang diketahui dan memperkirakan peringkat yang hilang sesuai dengan harapan intuitif. Keakuratan estimasi dapat ditingkatkan atau dikurangi dengan mengubah jumlah pengukuran, dan jumlah optimal pengukuran dapat ditentukan dalam praktik dengan memeriksa silang dan memilih kompromi yang masuk akal antara kompleksitas dan akurasi komputasi.
»Informasi lebih lanjut tentang buku ini dapat ditemukan di
situs web penerbit»
Isi»
KutipanKupon diskon 25% untuk penjaja -
Pembelajaran MesinSetelah pembayaran versi kertas buku, sebuah buku elektronik dikirim melalui email.