Kursus perkuliahan "Dasar-Dasar Pemrosesan Sinyal Digital"

Halo semuanya!

Seringkali orang menoleh kepada saya dengan pertanyaan tentang tugas-tugas dari bidang pemrosesan sinyal digital (DSP). Saya menceritakan secara rinci nuansa, menyarankan sumber informasi yang diperlukan. Tetapi semua pendengar, seperti yang ditunjukkan waktu, tidak memiliki tugas dan contoh praktis dalam proses mempelajari bidang ini. Dalam hal ini, saya memutuskan untuk menulis kursus interaktif singkat tentang pemrosesan sinyal digital dan memasukkannya ke dalam domain publik .

Sebagian besar materi pelatihan untuk presentasi visual dan interaktif diimplementasikan menggunakan Jupyter Notebook . Diasumsikan bahwa pembaca memiliki pengetahuan dasar tentang bidang matematika yang lebih tinggi, serta sedikit perintah bahasa pemrograman Python.

Daftar kuliah

Kursus ini berisi materi dalam bentuk kuliah jadi tentang berbagai topik dari bidang pemrosesan sinyal digital. Materi disajikan menggunakan pustaka Python (numpy, scipy, paket matplotlib, dll.). Informasi dasar untuk kursus ini diambil dari kuliah saya, yang saya, sebagai mahasiswa pascasarjana, berikan kepada mahasiswa Institut Energi Moskow (NRU MEI). Sebagian informasi dari kuliah ini digunakan pada seminar pelatihan di Pusat Elektronik Kontemporer , di mana saya bertindak sebagai dosen. Selain itu, materi ini mencakup terjemahan berbagai artikel ilmiah, kompilasi informasi dari sumber-sumber terpercaya dan literatur tentang pemrosesan sinyal digital, serta dokumentasi resmi tentang paket aplikasi dan fungsi built-in dari scipy dan numpy libraries di Python.

Untuk pengguna MATLAB (GNU Octave), menguasai materi dari sudut pandang kode program tidak sulit, karena fungsi utama dan atributnya sebagian besar identik dan mirip dengan metode dari pustaka Python.

Semua bahan dikelompokkan berdasarkan topik utama pemrosesan sinyal digital:

1. Sinyal: analog, diskrit, digital. Konversi z
2. Transformasi Fourier: amplitudo dan sinyal fase, DFT dan FFT,
3. Konvolusi dan korelasi. Konvolusi linier dan siklik. Konvolusi cepat
4. Proses acak. Kebisingan putih. Fungsi kepadatan probabilitas
5. Sinyal deterministik. Modulasi: AM, FM, FM, LFM. Manipulasi
6. Penyaringan Sinyal: filter IIR, FIR
7. Fungsi jendela dalam tugas penyaringan. Deteksi sinyal lemah.
8. Resampling: penipisan dan interpolasi. Filter CIC, filter rata-rata bergerak

Daftar kuliah sudah cukup tetapi, tentu saja, tidak lengkap untuk perkenalan dengan bidang DSP. Dengan waktu luang, saya berencana untuk mendukung dan mengembangkan proyek ini.

Di mana menemukan?

Semua bahan benar - benar gratis dan tersedia sebagai gudang terbuka di github saya sebagai proyek sumber terbuka . Materi disajikan dalam dua format - dalam bentuk Notebook Jupyter untuk pekerjaan interaktif, belajar dan mengedit, dan dalam bentuk file HTML yang dikompilasi dari notebook ini (setelah mengunduh dari github mereka memiliki format yang cukup cocok untuk membaca dan mencetak).

Berikut ini adalah deskripsi yang sangat singkat dari bagian-bagian kursus dengan penjelasan singkat, istilah dan definisi. Informasi dasar tersedia di kuliah awal, di sini hanya tinjauan singkat!

Sinyal. Konversi z

Bagian pengantar, yang berisi informasi dasar tentang jenis sinyal. Konsep urutan diskrit, fungsi delta, dan fungsi Heaviside (unit jump) diperkenalkan.

Semua sinyal sesuai dengan metode presentasi pada set dapat dibagi menjadi empat kelompok:

• analog - dijelaskan oleh fungsi terus menerus dalam waktu,
• diskrit - terputus dalam waktu dengan langkah yang ditentukan oleh pengambilan sampel,
• terkuantisasi - memiliki seperangkat level hingga (biasanya dalam amplitudo),
• digital - kombinasi sifat-sifat sinyal diskrit dan terkuantisasi.

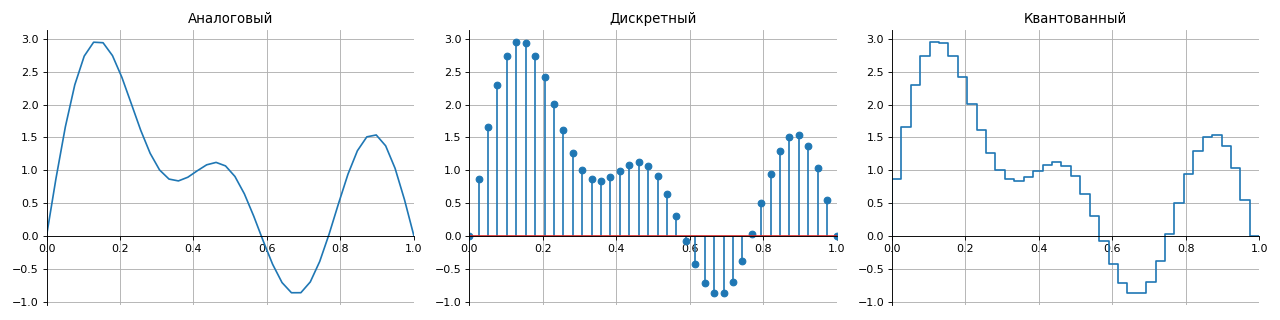
Untuk rekonstruksi yang benar dari sinyal analog dari sinyal digital tanpa distorsi dan kehilangan, teorema pengambilan sampel yang dikenal sebagai teorema Kotelnikov (Nyquist-Shannon) digunakan.

Setiap sinyal kontinu dengan spektrum terbatas dapat dipulihkan secara unik dan tanpa kehilangan dari sampel terpisahnya yang diambil dengan frekuensi yang benar-benar lebih besar dari dua kali frekuensi atas spektrum sinyal kontinyu.

Interpretasi seperti itu valid asalkan fungsi waktu yang kontinyu menempati pita frekuensi dari 0 hingga nilai frekuensi atas. Jika langkah kuantisasi dan diskritisasi dipilih secara salah, sinyal akan terdistorsi dari analog ke diskrit.

Juga di bagian ini, transformasi-Z dan sifat-sifatnya dijelaskan, dan representasi dari sekuens diskrit dalam bentuk-Z ditampilkan.

Contoh urutan diskrit terbatas:

x(nT) = {2, 1, -2, 0, 2, 3, 1, 0} 

.
Contoh dari urutan yang sama dalam bentuk-Z:

X (z) = 2 + z ^-1 - 2z ^-2 + 2z ^-4 + 3z ^-5 + 1z ^-6

Transformasi Fourier. Properti DFT dan FFT

Bagian ini menjelaskan konsep domain waktu dan frekuensi dari suatu sinyal. Definisi transformasi Fourier diskrit (DFT) diperkenalkan. DFT langsung dan terbalik dan sifat utamanya dipertimbangkan. Ditampilkan adalah transisi dari DFT ke algoritma Fourier transform (FFT) cepat dalam basis 2 (algoritma penipisan dalam frekuensi dan waktu). Mencerminkan efektivitas FFT dibandingkan dengan DFT.

Secara khusus, bagian ini menjelaskan paket Python scipy.ffpack untuk menghitung berbagai transformasi Fourier (sinus, cosinus, langsung, terbalik, multidimensi, nyata).

Transformasi Fourier memungkinkan Anda untuk mewakili fungsi apa pun sebagai serangkaian sinyal harmonik! Transformasi Fourier adalah dasar dari metode konvolusi dan desain korelator digital, secara aktif digunakan dalam analisis spektral, dan digunakan ketika bekerja dengan angka yang panjang.

Fitur spektrum sinyal diskrit:
1. Kepadatan spektral dari sinyal diskrit adalah fungsi periodik dengan periode yang sama dengan frekuensi sampling.
2. Jika urutan diskrit adalah nyata , maka modulus kepadatan spektral dari urutan tersebut adalah fungsi genap , dan argumennya adalah fungsi frekuensi ganjil .

Spektrum Sinyal Harmonik:

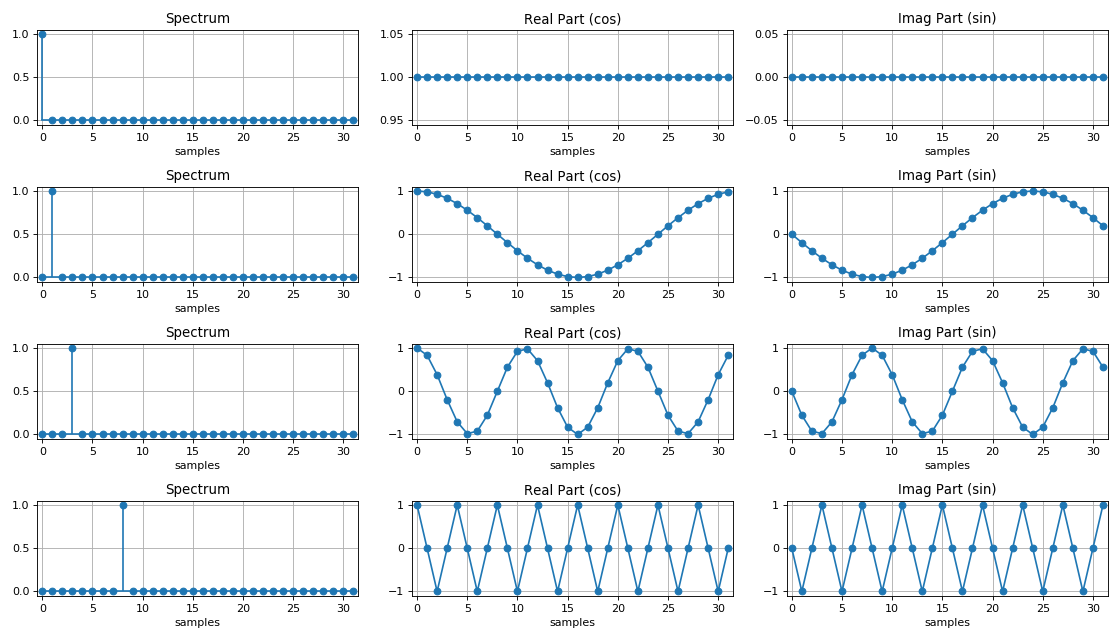
Perbandingan kemanjuran DFT dan FFT

Efisiensi algoritma FFT dan jumlah operasi yang dilakukan secara linear tergantung pada panjang urutan N:


Seperti yang Anda lihat, semakin lama panjang konversi, semakin besar penghematan dalam sumber daya komputasi (dalam hal kecepatan pemrosesan atau jumlah unit perangkat keras)!

Bentuk gelombang sembarang dapat direpresentasikan sebagai satu set sinyal harmonik dari frekuensi yang berbeda. Dengan kata lain, sinyal bentuk kompleks dalam domain waktu memiliki satu set sampel kompleks dalam domain frekuensi, yang disebut * harmonik *. Sampel-sampel ini mengekspresikan amplitudo dan fase efek harmonik pada frekuensi tertentu. Semakin besar himpunan harmonik dalam domain frekuensi, semakin akurat bentuk gelombang kompleks muncul.

Konvolusi dan korelasi

Bagian ini memperkenalkan konsep korelasi dan konvolusi untuk urutan acak dan deterministik diskrit. Hubungan antara fungsi autokorelasi dan korelasi silang dengan konvolusi ditunjukkan. Sifat-sifat konvolusi dijelaskan, khususnya, metode konvolusi linier dan siklik dari sinyal diskrit dengan analisis rinci pada contoh sekuens diskrit dipertimbangkan. Selain itu, metode untuk menghitung konvolusi "cepat" menggunakan algoritma FFT ditampilkan.

Dalam masalah nyata, pertanyaan sering diajukan tentang tingkat kesamaan dari satu proses ke proses lainnya atau tentang independensi dari satu proses dari proses lainnya. Dengan kata lain, diperlukan untuk menentukan hubungan antara sinyal, yaitu, untuk menemukan korelasi . Metode korelasi digunakan dalam berbagai tugas: pencarian sinyal, visi komputer dan pemrosesan gambar, dalam masalah radar untuk menentukan karakteristik target dan menentukan jarak ke objek. Selain itu, korelasi digunakan untuk mencari sinyal lemah dalam noise.

Konvolusi menggambarkan interaksi sinyal satu sama lain. Jika salah satu sinyal adalah respons impuls dari filter, maka konvolusi urutan input dengan respons impuls tidak lain adalah reaksi rangkaian terhadap aksi input. Dengan kata lain, sinyal yang dihasilkan mencerminkan bagian dari sinyal melalui filter.

Fungsi autokorelasi (ACF) digunakan dalam pengkodean informasi. Pilihan urutan pengkodean sesuai dengan parameter panjang, frekuensi dan bentuk sebagian besar disebabkan oleh sifat korelasi dari urutan ini. Urutan kode terbaik memiliki probabilitas terendah untuk deteksi atau operasi palsu (untuk mendeteksi sinyal, untuk perangkat ambang) atau sinkronisasi palsu (untuk mentransmisikan dan menerima urutan kode).

Bagian ini menyajikan tabel yang membandingkan efektivitas konvolusi cepat dan konvolusi yang dihitung dengan rumus langsung (dengan jumlah perkalian nyata).

Seperti yang Anda lihat, untuk panjang FFT hingga 64, konvolusi cepat hilang ke metode langsung. Namun, dengan peningkatan panjang FFT, hasilnya berubah ke arah yang berlawanan - konvolusi cepat mulai mengungguli metode langsung. Jelas, semakin lama FFT, semakin baik gain dalam metode frekuensi.

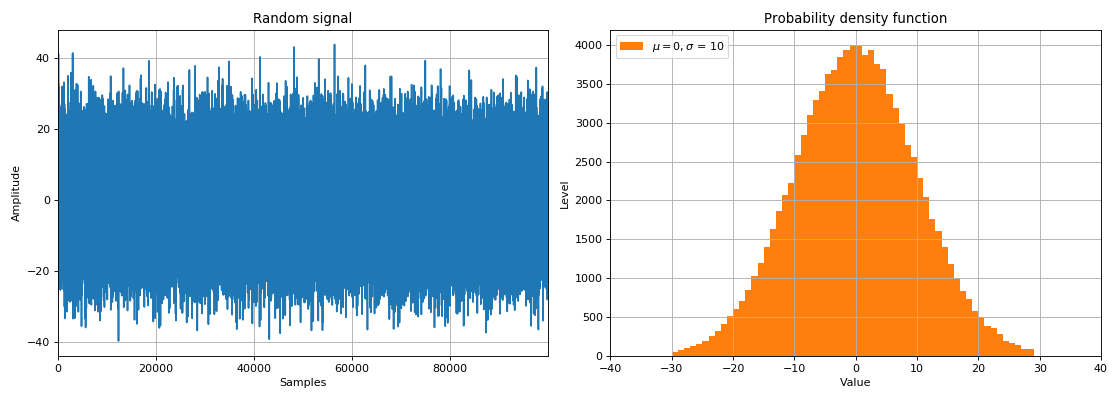
Sinyal dan Kebisingan Acak

Pada bagian ini, konsep sinyal acak, kepadatan probabilitas, hukum distribusi acak diperkenalkan. Momen matematika dianggap - mean (ekspektasi matematis) dan varians (atau akar dari kuantitas ini adalah standar deviasi). Juga di bagian ini, distribusi normal dan konsep terkait white noise dianggap sebagai sumber utama noise (gangguan) selama pemrosesan sinyal.

Sinyal acak adalah fungsi waktu yang nilainya tidak diketahui sebelumnya dan hanya dapat diprediksi dengan beberapa probabilitas . Karakteristik utama dari sinyal acak meliputi:

• hukum distribusi (waktu tinggal relatif dari nilai sinyal dalam interval tertentu),
• distribusi spektral daya sinyal.

Dalam tugas DSP, sinyal acak dibagi menjadi dua kelas:

• noise - fluktuasi acak yang terdiri dari serangkaian frekuensi dan amplitudo yang berbeda,
• sinyal membawa informasi, untuk pemrosesan yang diperlukan untuk menggunakan metode probabilistik.

Dengan menggunakan variabel acak, kita dapat mensimulasikan efek medium nyata pada perpindahan sinyal dari sumber ke penerima data. Ketika sebuah sinyal melewati beberapa tautan bising, yang disebut white noise ditambahkan ke sinyal. Sebagai aturan, kerapatan spektral noise tersebut terdistribusi secara merata (merata) pada semua frekuensi, dan nilai noise dalam domain waktu terdistribusi normal (hukum distribusi Gaussian). Karena white noise ditambahkan secara fisik ke amplitudo sinyal dalam sampel waktu yang dipilih, ini disebut Additive white Gaussian noise (AWGN).

Sinyal, Modulasi dan Manipulasi

Bagian ini menunjukkan metode dasar untuk mengubah satu atau lebih parameter sinyal harmonik. Konsep amplitudo, frekuensi dan modulasi fase diperkenalkan. Secara khusus, modulasi frekuensi linier yang digunakan dalam masalah radar disorot. Karakteristik utama dari sinyal, spektrum sinyal termodulasi tergantung pada parameter modulasi ditampilkan.



Untuk kenyamanan, serangkaian fungsi telah dibuat dengan Python yang mengimplementasikan jenis modulasi di atas. Contoh implementasi sinyal kicauan:

 def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs): """ Create Chirp signal Parameters ---------- amp : float Signal magnitude beta : float Modulation bandwidth: beta < N for complex, beta < 0.5N for real freq : float or int Linear frequency of signal period : integer Number of points for signal (same as period) kwargs : bool Complex signal if is_complex = True Modulated by half-sine wave if is_modsine = True """ is_complex = kwargs.get('is_complex', False) is_modsine = kwargs.get('is_modsine', False) t = np.linspace(0, 1, period) tt = np.pi * (freq * t + beta * t ** 2) if is_complex is True: res = amp * (np.cos(tt) + 1j * np.sin(tt)) else: res = amp * np.cos(tt) if is_modsine is True: return res * np.sin(np.pi * t) return res 

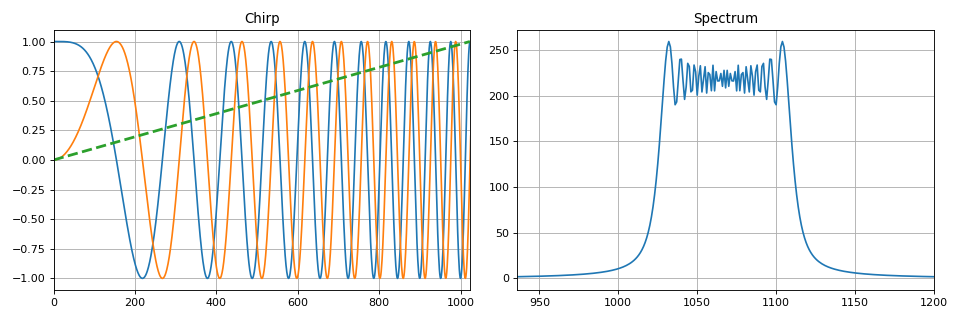
Juga di bagian ini dari teori transmisi jenis pesan diskrit dari modulasi digital - manipulasi dijelaskan. Seperti dalam kasus sinyal analog, urutan harmonik digital dapat dimanipulasi dalam amplitudo, fase dan frekuensi (atau beberapa parameter sekaligus).

Filter Digital - IIR dan FIR

Bagian yang cukup besar yang didedikasikan untuk penyaringan digital dari urutan diskrit. Dalam tugas pemrosesan sinyal digital, data mengalir melalui sirkuit yang disebut filter . Filter digital, seperti yang analog, memiliki karakteristik berbeda - frekuensi: respons frekuensi, respons fase, waktu: respons impuls, serta karakteristik transfer filter. Filter digital terutama digunakan untuk meningkatkan kualitas sinyal - untuk mengisolasi sinyal dari urutan data, atau untuk menurunkan sinyal yang tidak diinginkan - untuk menekan sinyal tertentu dalam urutan sampel yang masuk.



Bagian ini mencantumkan keuntungan dan kerugian utama dari filter digital (dibandingkan dengan analog). Konsep impuls dan karakteristik transfer filter diperkenalkan. Dua kelas filter dipertimbangkan - dengan respon impuls tak terbatas (IIR) dan respon impuls terbatas (FIR). Metode untuk merancang filter dalam bentuk kanonik dan langsung ditampilkan. Untuk filter FIR, pertanyaan tentang cara beralih ke formulir rekursif dipertimbangkan.



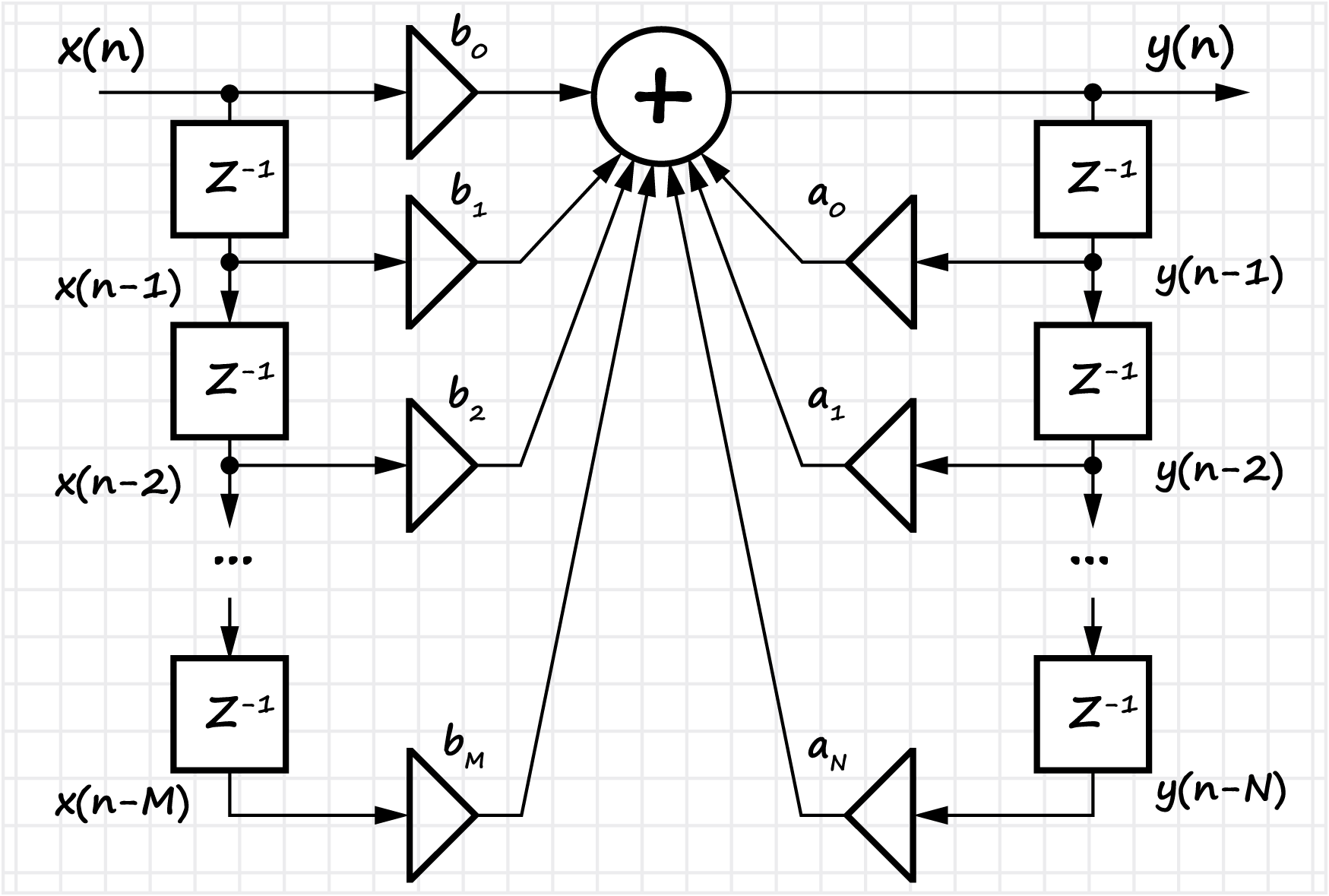
Untuk filter FIR, proses desain filter ditunjukkan dari tahap pengembangan spesifikasi teknis (dengan parameter utama yang ditunjukkan), hingga implementasi perangkat lunak dan perangkat keras - cari koefisien filter (dengan mempertimbangkan bentuk representasi dari angka, kedalaman bit, dll.). Definisi filter FIR simetris, respons fase linier dan hubungannya dengan konsep keterlambatan grup diperkenalkan.

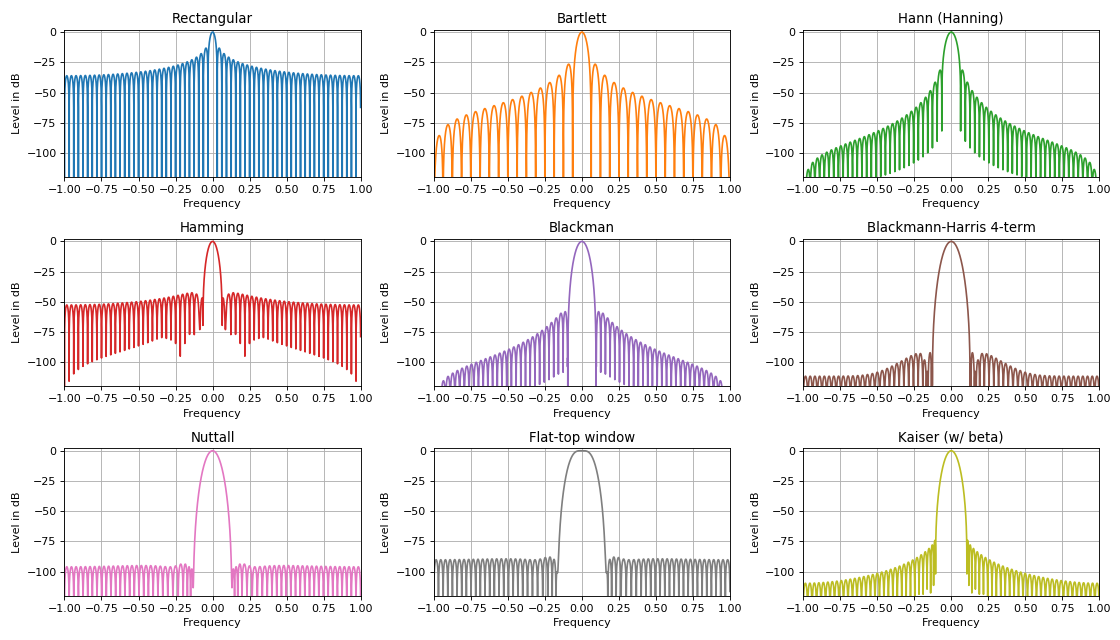
Fungsi jendela dalam tugas penyaringan

Dalam tugas pemrosesan sinyal digital, fungsi jendela berbagai bentuk digunakan, yang, ketika ditumpangkan pada sinyal dalam domain waktu, secara kualitatif dapat meningkatkan karakteristik spektralnya. Sejumlah besar berbagai jendela terutama disebabkan oleh salah satu fitur utama dari setiap hamparan jendela. Fitur ini dinyatakan dalam hubungan antara tingkat lobus samping dan lebar lobus sentral. Aturan:

Semakin kuat penekanan lobus samping spektrum, semakin luas lobus utama spektrum dan sebaliknya.

Salah satu aplikasi fungsi jendela: deteksi sinyal lemah terhadap latar belakang sinyal yang lebih kuat dengan menekan level lobus samping. Fungsi jendela utama dalam tugas DSP adalah ** triangular, sinusoidal, Lanczos, Hann, Hamming, Blackman, Harris, jendela Blackman-Harris, jendela flat-top, Natall, Gauss, jendela Kaiser ** dan banyak lainnya. Sebagian besar dari mereka diekspresikan melalui seri terbatas dengan menjumlahkan sinyal harmonik dengan bobot tertentu. Sinyal-sinyal semacam itu diimplementasikan dengan sempurna dalam praktik pada perangkat perangkat keras apa pun (sirkuit logika yang dapat diprogram atau pemroses sinyal).

Resampling. Penipisan dan interpolasi

Bagian ini membahas masalah pemrosesan sinyal multi-kecepatan - perubahan dalam frekuensi sampling. Pemrosesan sinyal multi-kecepatan (pemrosesan multirate) menunjukkan bahwa dalam proses konversi linear dari sinyal digital, dimungkinkan untuk mengubah frekuensi sampling ke arah penurunan atau peningkatan, atau dalam jumlah fraksional kali. Hal ini mengarah pada pemrosesan sinyal yang lebih efisien, karena membuka kemungkinan menggunakan frekuensi sampling minimum yang diijinkan dan, sebagai hasilnya, pengurangan yang signifikan dalam kinerja komputasi yang diperlukan dari sistem digital yang dirancang.

Penipisan (penipisan) - downsampling. Interpolasi - meningkatkan laju pengambilan sampel.

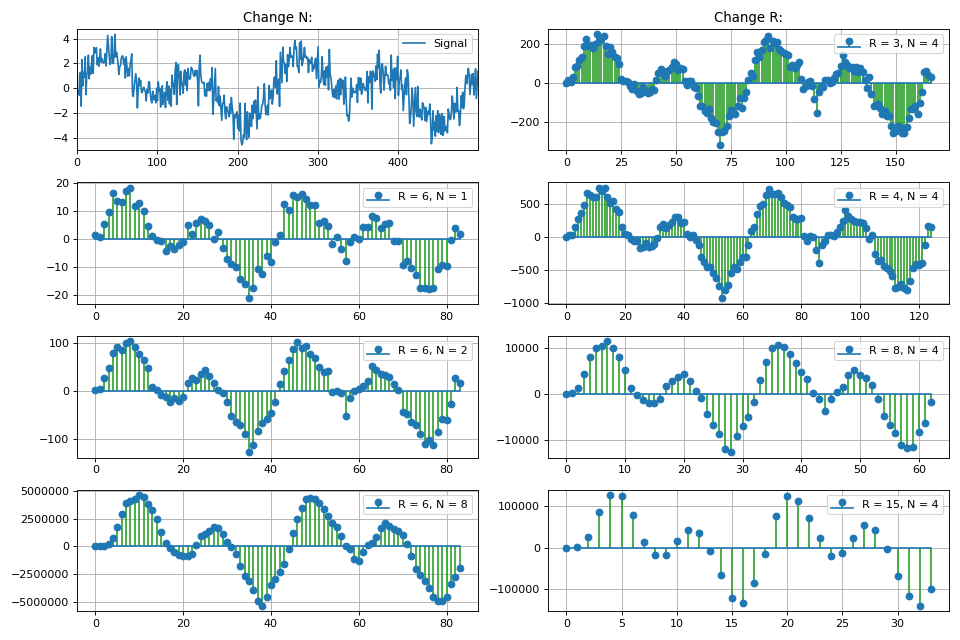
Bagian ini juga mempertimbangkan kelas filter FIR homogen, yang disebut filter integral-sisir (CIC, Cascaded integrator - comb). Implementasi, sifat dasar dan fitur filter CIC ditampilkan. Karena linearitas operasi matematika yang terjadi dalam filter CIC, dimungkinkan untuk membuat beberapa filter berturut-turut, yang memberikan penurunan proporsional pada tingkat lobus samping, tetapi juga meningkatkan "penyumbatan" pada lobus utama dari karakteristik frekuensi amplitudo.



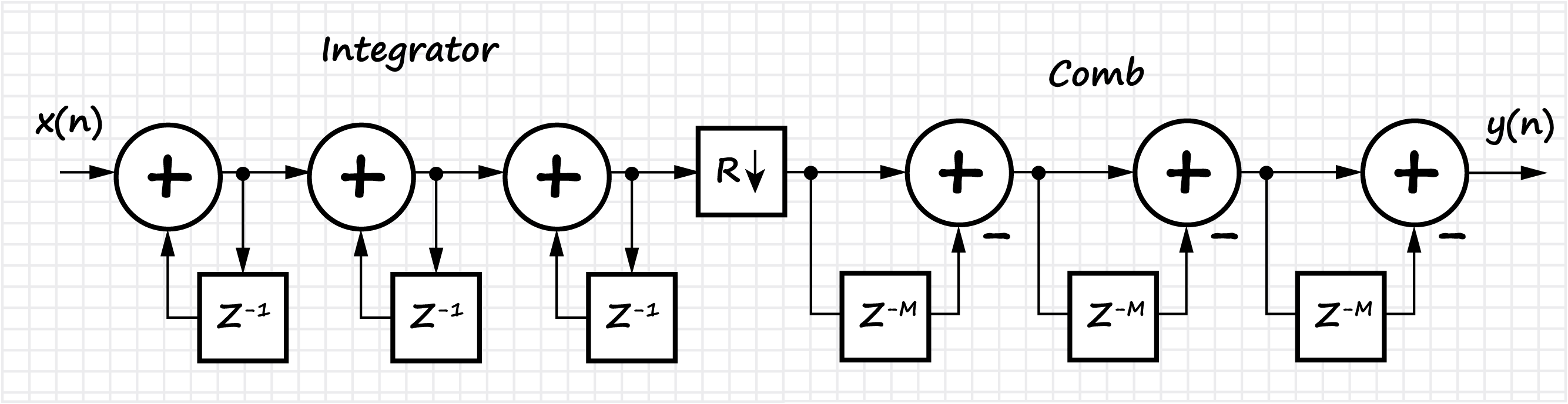
Grafik dari respons frekuensi filter tergantung pada koefisien penipisan:



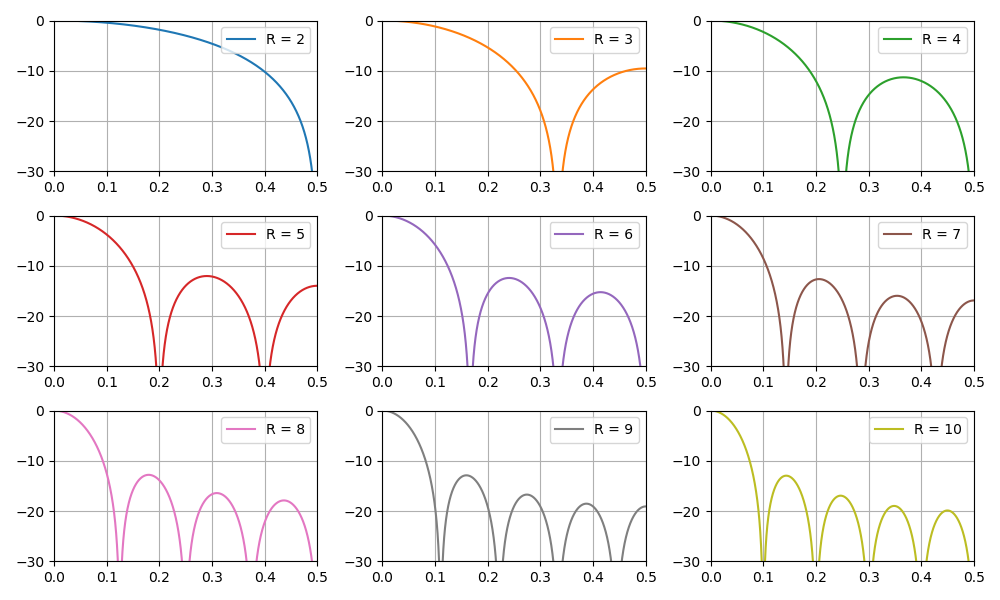
Juga di bagian ini kita membahas masalah peningkatan kedalaman bit data pada output filter CIC, tergantung pada parameternya. Ini sangat penting dalam tugas implementasi perangkat lunak, khususnya pada FPGA.

Untuk implementasi praktis filter CIC di Python, kelas CicFilter yang terpisah telah dikembangkan yang mengimplementasikan metode penipisan dan interpolasi. Juga ditampilkan adalah perubahan laju sampel menggunakan metode bawaan dari paket Python yang cerdik.





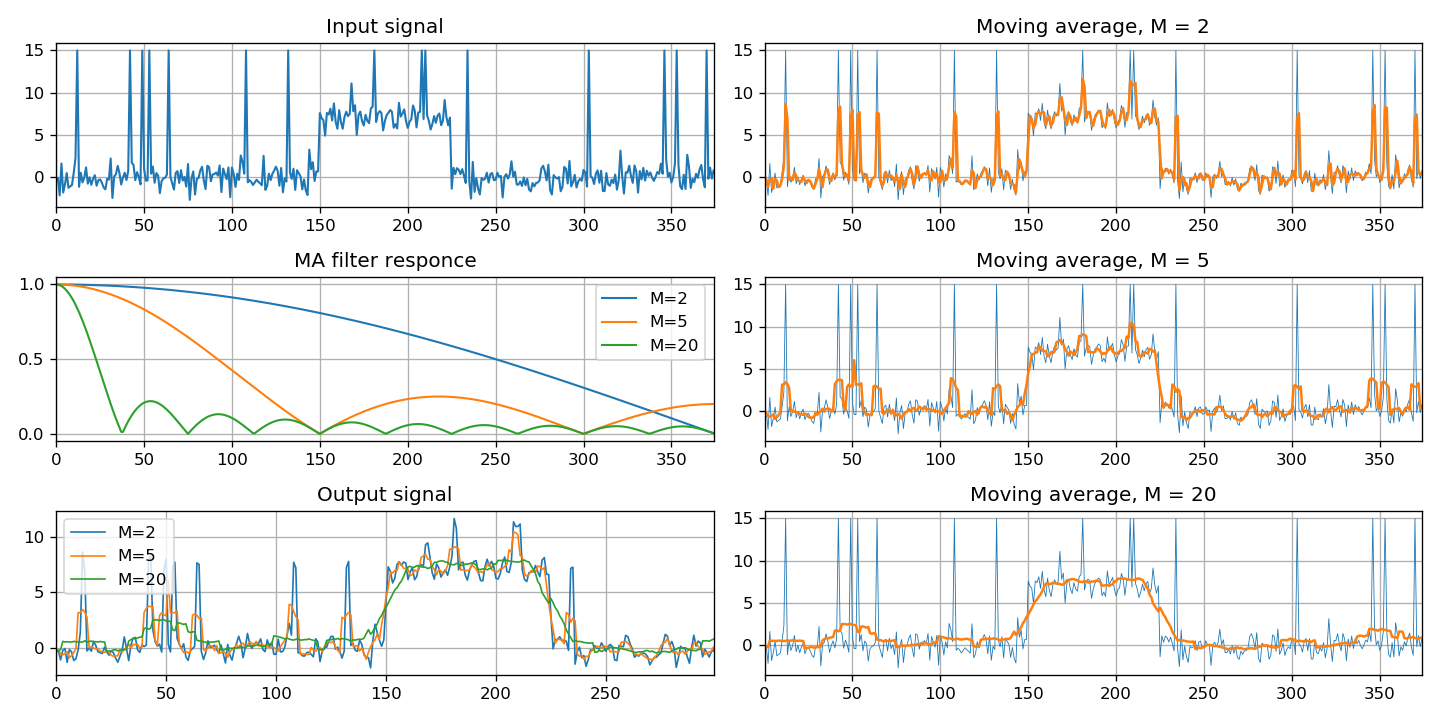
Akhirnya, bagian ini menyediakan kelas filter khusus - rata-rata bergerak. Tiga metode implementasi ditunjukkan: melalui konvolusi sinyal, menggunakan filter FIR dan filter IIR.

Kesimpulan

Saya harap kursus kuliah ini bersama dengan artikel saya sebelumnya tentang pemrosesan sinyal FPGA digital akan membawa manfaat praktis dan membantu pembaca lebih memahami dasar-dasar pemrosesan sinyal digital. Proyek ini akan ditingkatkan dan dilengkapi dengan materi baru yang bermanfaat dan tidak kalah menarik. Ikuti perkembangannya!

Selain materi ini, saya mendukung dan mengembangkan proyek saya pada modul DSP utama (dengan Python). Ini berisi paket untuk menghasilkan berbagai sinyal, kelas filter CIC untuk masalah penipisan dan interpolasi, algoritma untuk menghitung koefisien filter FIR yang diperbaiki, filter rata-rata bergerak, algoritma untuk menghitung FFT yang sangat panjang melalui metode konversi dua dimensi (yang terakhir ini sangat berguna ketika bekerja dengan implementasi perangkat keras pada FPGA) .

Terima kasih atas perhatian anda!