Terjemahan artikel disiapkan untuk siswa kursus "Matematika untuk Ilmu Data"
Anotasi
Artikel ini membahas tugas menemukan kontur wajah untuk satu gambar. Kami menunjukkan bagaimana ansambel pohon regresi dapat digunakan untuk memprediksi posisi kontur wajah langsung dari subset intensitas piksel yang tersebar, mencapai kinerja super secara real time dengan prediksi berkualitas tinggi. Kami menyajikan struktur umum berdasarkan peningkatan gradien untuk mempelajari ansambel pohon regresi yang mengoptimalkan jumlah kerugian kuadrat dan, tentu saja, memproses data yang hilang atau sebagian ditandai. Kami akan menunjukkan bagaimana penggunaan distribusi yang tepat yang memperhitungkan struktur data gambar membantu dalam pemilihan kontur yang efisien. Berbagai strategi regularisasi dan kepentingannya dalam perjuangan melawan pelatihan ulang juga sedang diselidiki. Selain itu, kami menganalisis efek dari jumlah data pelatihan pada keakuratan prakiraan dan menguji pengaruh peningkatan data menggunakan data yang disintesis.
1. Pendahuluan
Dalam artikel ini, kami menyajikan algoritma baru yang mencari kontur wajah dalam milidetik dan mencapai akurasi yang lebih unggul atau sebanding dengan metode modern pada set data standar. Peningkatan kecepatan dibandingkan dengan metode sebelumnya adalah konsekuensi dari identifikasi komponen utama dari algoritma sebelumnya untuk pencarian kontur wajah dan inklusi berikutnya dalam bentuk yang dioptimalkan dalam kaskade model regresi dengan bandwidth tinggi, disetel menggunakan gradient boosting.
Kami menunjukkan, seperti yang telah kami lakukan sebelumnya [8, 2], bahwa pencarian untuk kontur wajah dapat dilakukan menggunakan kaskade model regresi. Dalam kasus kami, setiap model regresi dalam kaskade secara efektif memprediksi bentuk wajah berdasarkan perkiraan awal dan intensitas kumpulan piksel yang diindeks relatif terhadap perkiraan awal ini. Pekerjaan kami didasarkan pada sejumlah besar studi yang dilakukan selama dekade terakhir, yang telah menyebabkan kemajuan yang signifikan dalam tugas menemukan kontur wajah [9, 4, 13, 7, 15, 1, 16, 18, 3, 6, 19]. Secara khusus, kami telah memasukkan dalam model regresi yang disetel kami dua elemen kunci yang hadir dalam beberapa algoritma yang sukses di bawah ini, dan sekarang kami merinci elemen-elemen ini.
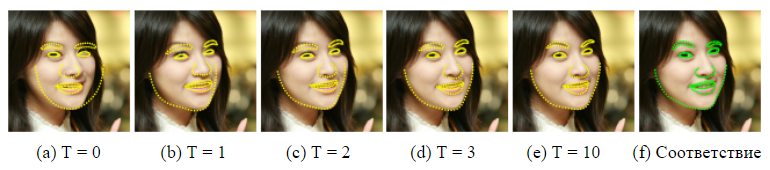
Gambar 1. Hasil yang dipilih pada dataset HELEN. Untuk mendeteksi 194 titik kunci (landmark) pada wajah dalam satu gambar dalam milidetik, ensemble pohon regresi acak digunakan.
Yang pertama berkisar pada pengindeksan intensitas piksel relatif terhadap perkiraan bentuk wajah saat ini. Fitur-fitur khusus dalam representasi vektor dari gambar wajah dapat sangat bervariasi karena deformasi bentuk, dan karena faktor-faktor yang mengganggu seperti perubahan kondisi pencahayaan. Ini membuatnya sulit untuk secara akurat memprediksi bentuk menggunakan fungsi-fungsi ini. Dilema adalah kita membutuhkan tanda yang dapat diandalkan untuk memprediksi bentuk secara akurat, dan di sisi lain, kita membutuhkan perkiraan bentuk yang akurat untuk mengekstraksi tanda yang dapat diandalkan. Dalam karya sebelumnya [4, 9, 5, 8], serta dalam karya ini, pendekatan iteratif (kaskade) digunakan untuk menyelesaikan masalah ini. Alih-alih mundur parameter bentuk berdasarkan fitur yang diekstraksi dalam sistem koordinat gambar global, gambar dikonversi ke sistem koordinat dinormalisasi berdasarkan perkiraan bentuk saat ini, dan kemudian tanda diekstraksi untuk memprediksi vektor pembaruan untuk parameter bentuk. Proses ini biasanya diulang beberapa kali hingga konvergensi.
Yang kedua meneliti bagaimana menangani kompleksitas masalah penjelasan / prediksi. Selama pengujian, algoritma pencarian kontur harus memprediksi bentuk wajah - vektor dimensi tinggi yang sesuai dengan data gambar dan model bentuk kami. Masalahnya adalah nonconvex dengan banyak optima lokal. Algoritma yang berhasil [4, 9] menyelesaikan masalah ini, dengan asumsi bahwa bentuk yang diprediksi harus terletak pada subruang linier yang dapat dideteksi, misalnya, dengan menemukan komponen utama dari formulir pelatihan. Asumsi ini secara signifikan mengurangi jumlah bentuk potensial yang dipertimbangkan selama penjelasan, dan dapat membantu menghindari optima lokal.
Sebuah karya baru-baru ini [8, 11, 2] mengeksploitasi fakta bahwa kelas tertentu dari regressor dijamin untuk membuat prediksi yang terletak pada subruang linier yang ditentukan oleh bentuk pembelajaran, dan tidak perlu adanya pembatasan tambahan. Adalah penting bahwa model regresi kami memiliki dua elemen ini.
Kedua faktor ini terkait dengan pelatihan efektif kami dalam model regresi. Kami mengoptimalkan fungsi kerugian terkait dan melakukan pemilihan fitur berdasarkan data. Secara khusus, kami melatih setiap regressor menggunakan gradient boosting [10] menggunakan fungsi kerugian kuadratik, fungsi kerugian yang sama yang ingin kami meminimalkan selama pengujian. Himpunan piksel jarang yang digunakan sebagai input ke regresi dipilih menggunakan kombinasi algoritma peningkatan gradien dan probabilitas a priori dari jarak antara pasangan piksel input. Distribusi apriori memungkinkan algoritma peningkatan untuk menyelidiki secara efisien sejumlah besar fitur yang relevan. Hasilnya adalah kaskade regressor yang dapat melokalkan landmark wajah ketika diinisialisasi dari depan.
Kontribusi utama dari artikel ini adalah:
- Metode baru untuk menemukan kontur wajah, berdasarkan ansambel pohon regresi (pohon keputusan), yang melakukan pemilihan fitur invarian dari formulir, sambil meminimalkan fungsi kehilangan yang sama selama pelatihan yang ingin kami meminimalkan selama pengujian.
- Kami menyajikan ekstensi alami dari metode kami yang memproses label yang hilang atau tidak ditentukan.
- Hasil kuantitatif dan kualitatif disajikan, yang mengkonfirmasi bahwa metode kami memberikan perkiraan berkualitas tinggi, jauh lebih efektif daripada metode terbaik sebelumnya (Gambar 1).
- Pengaruh jumlah data pelatihan, penggunaan data yang diberi label sebagian dan data yang digeneralisasi pada kualitas perkiraan dianalisis.
2. Metode
Artikel ini menyajikan algoritma untuk secara akurat menilai posisi landmark wajah (poin utama) dalam hal efisiensi komputasi. Seperti dalam karya sebelumnya [8, 2], kaskade regressor digunakan dalam metode kami. Pada bagian selanjutnya dari bagian ini, kami menjelaskan detail bentuk komponen individu dari kaskade dan bagaimana kami melakukan pelatihan.
2.1. Kaskade regresi
Pertama kami memperkenalkan beberapa notasi. Biarkan 
, koordinat y dari landmark ke-i dari wajah pada gambar I. Kemudian vektor 
menunjukkan koordinat semua wajah p dalam I. Seringkali dalam artikel ini kita menyebut vektor S bentuk. Kami menggunakan 
untuk menunjukkan peringkat kami saat ini S. Setiap regresi 
(·, ·) Dalam kaskade memprediksi pembaruan vektor dari gambar dan yang ditambahkan ke evaluasi formulir saat ini Untuk meningkatkan peringkat:
) (1)
Titik kunci dari kaskade adalah bahwa sang regresor membuat perkiraan berdasarkan atribut seperti intensitas piksel yang dihitung oleh I dan diindeks relatif terhadap perkiraan bentuk saat ini . Ini memperkenalkan semacam invarian geometris ke dalam proses, dan saat Anda maju melalui kaskade, Anda bisa lebih yakin bahwa lokasi semantik yang tepat pada wajah diindeks. Kami nanti akan menjelaskan bagaimana pengindeksan ini dilakukan.
Harap dicatat bahwa rentang output yang diperpanjang oleh ansambel dijamin terletak pada subruang linier dari data pelatihan jika perkiraan awal 
milik ruang ini. Oleh karena itu, kami tidak perlu memperkenalkan batasan tambahan pada prediksi, yang sangat menyederhanakan metode kami. Bentuk awal hanya dapat dipilih sebagai bentuk tengah dari data pelatihan, dipusatkan dan diskalakan sesuai dengan output dari kotak pembatas dari detektor wajah umum.
Untuk mendidik semua orang kami menggunakan algoritma peningkatan gradien untuk pohon dengan jumlah kerugian kuadratik, seperti yang dijelaskan dalam [10]. Sekarang kami akan memberikan detail detail dari proses ini.
2.2. Latih setiap regressor dalam sebuah riam
Misalkan kita memiliki data pelatihan 
dimana semua orang 
adalah gambar wajah, dan 
vektor bentuknya. Untuk mengetahui fungsi regresi pertama 
dalam kaskade, kami membuat dari triplet data pelatihan kami dari gambar wajah, prakiraan bentuk awal dan langkah pembaruan target, mis. 
) dimana
(2)
(3) dan
(4)
untuk i = 1, ..., N.
Kami menetapkan jumlah total kembar tiga ini ke N = nR, di mana R adalah jumlah inisialisasi yang digunakan pada gambar Ii. Setiap perkiraan bentuk awal untuk gambar dipilih secara merata 
tanpa penggantian.
Pada data ini kami melatih fungsi regresi 
(Lihat Algoritma 1) menggunakan gradien meningkatkan pohon dengan jumlah kerugian kuadratik. Set triplet pelatihan kemudian diperbarui untuk memberikan data pelatihan. 
% 20) untuk penerus berikutnya 
dalam kaskade dengan mengatur (dengan t = 0).
% 20) (5)
(6)
Proses ini diulangi sampai riam T regressor dilatih. 
yang dalam kombinasi memberikan tingkat akurasi yang cukup.
Seperti yang ditunjukkan, masing-masing regresi belajar menggunakan algoritma peningkatan pohon gradien. Harus diingat bahwa fungsi kerugian kuadratik digunakan, dan residu yang dihitung dalam loop dalam berhubungan dengan gradien dari fungsi kehilangan ini yang diperkirakan dalam setiap sampel pelatihan. Perumusan algoritma mencakup parameter laju pembelajaran 0 <ν ≤ 1, juga dikenal sebagai koefisien regularisasi. Pengaturan ν <1 membantu untuk memerangi konfigurasi ulang dan biasanya mengarah ke regressor yang menggeneralisasi jauh lebih baik daripada yang dilatih dengan ν = 1 [10].
Algoritma Belajar 1 dalam kaskade
Kami memiliki data pelatihan 
dan tingkat pembelajaran (koefisien regularisasi) 0 <ν <1
- Inisialisasi
- untuk k = 1, ..., K:
a) kita atur untuk i = 1, ...,
b) Kami menyesuaikan pohon regresi ke target 
dengan fungsi regresi yang lemah 
.
c) Memperbarui 
- Kesimpulan
2.3. Pohon regressor
Pada intinya setiap fungsi regresi rt adalah regressor mirip pohon yang cocok untuk target residual selama algoritma peningkatan gradien. Sekarang kita akan melihat detail implementasi yang paling penting untuk melatih setiap pohon regresi.
Pada setiap simpul pemisahan di pohon regresi, kami membuat keputusan berdasarkan nilai ambang perbedaan antara intensitas dua piksel. Pixel yang digunakan dalam pengujian berada di posisi u dan v ketika ditetapkan dalam sistem koordinat bentuk tengah. Untuk gambar wajah dengan bentuk sewenang-wenang, kami ingin mengindeks poin yang memiliki posisi yang sama relatif terhadap bentuknya seperti u dan v, untuk bentuk rata-rata. Untuk melakukan ini, sebelum mengekstraksi elemen, gambar dapat dideformasi menjadi bentuk tengah berdasarkan pada perkiraan bentuk saat ini. Karena kami hanya menggunakan representasi gambar yang sangat jarang, jauh lebih efisien untuk mengubah bentuk pengaturan titik daripada keseluruhan gambar. Selain itu, perkiraan kasar deformasi dapat dibuat hanya menggunakan transformasi kesamaan global di samping perpindahan lokal, seperti yang diusulkan dalam [2].
Rincian persisnya adalah sebagai berikut. Biarkan 
Apakah indeks tengara pada wajah dalam bentuk tengah paling dekat dengan Anda, dan tentukan perpindahannya dari Anda sebagai 
.
Kemudian untuk bentuk Si didefinisikan dalam gambar posisi dalam , yang secara kualitatif mirip dengan u pada gambar bentuk sedang, didefinisikan sebagai
(7)
dimana dan 
- skala dan matriks rotasi dari transformasi kesamaan yang mentransformasikannya masuk 
, bentuk tengah.
Skala dan rotasi diminimalkan
(8)
jumlah kuadrat antara titik-titik tengara bentuk tengah, 
dan point warp. 
didefinisikan dengan cara yang sama.
Secara formal, setiap divisi adalah solusi yang mencakup 3 parameter θ = (τ, u, v), dan diterapkan pada setiap pelatihan dan contoh pengujian sebagai
(9)
dimana 
dan ditentukan dengan menggunakan skala dan matriks rotasi yang paling merusak 
masuk sesuai dengan persamaan (7). Dalam praktiknya, tugas dan perpindahan lokal ditentukan pada tahap pelatihan. Perhitungan transformasi kesamaan, selama pengujian bagian paling mahal dari proses ini, dilakukan hanya sekali di setiap tingkat kaskade.
2.3.2 Pemilihan partisi nodal
Untuk setiap pohon regresi, kami memperkirakan fungsi dasar dengan fungsi linear piecewise, di mana vektor konstan cocok untuk setiap node hingga. Untuk melatih pohon regresi, kami secara acak menghasilkan sekumpulan partisi yang cocok, yaitu, θ, di setiap node. Kemudian kami dengan penuh semangat memilih θ * dari kandidat ini, yang meminimalkan jumlah kesalahan kuadratik. Jika Q adalah sekumpulan indeks contoh pelatihan dalam sebuah simpul, maka ini berhubungan dengan minimalisasi
(10)
dimana 
- indeks contoh yang dikirim ke simpul kiri karena keputusan θ, 
Apakah vektor semua residu dihitung untuk gambar i dalam algoritma peningkatan gradien, dan
untuk 
(11)
Partisi optimal dapat ditemukan dengan sangat efisien, karena jika kita mengubah persamaan (10) dan menghilangkan faktor-faktor yang tidak bergantung pada θ, kita dapat melihat bahwa
Di sini kita hanya perlu menghitung 
ketika mengevaluasi berbagai θ, sejak 
dapat dihitung dari sasaran rata-rata di simpul induk μ dan sebagai berikut:
2.3.3 Pemilihan karakteristik
Solusi di setiap node didasarkan pada nilai ambang dari perbedaan dalam nilai intensitas dalam sepasang piksel. Ini adalah tes yang cukup sederhana, tetapi jauh lebih efektif daripada nilai ambang batas dengan intensitas tunggal, karena relatif tidak sensitif terhadap perubahan pencahayaan global. Sayangnya, kelemahan menggunakan perbedaan piksel adalah bahwa jumlah kandidat pemisahan potensial (fitur) kuadrat sehubungan dengan jumlah piksel dalam gambar rata-rata. Hal ini membuat sulit untuk menemukan barang yang bagus tanpa mencari dalam jumlah yang besar. Namun, faktor pembatas ini bisa agak melemah, dengan mempertimbangkan struktur data gambar.
Kami memperkenalkan distribusi eksponensial
(12)
oleh jarak antara piksel yang digunakan dalam pemisahan untuk mendorong pemilihan pasangan piksel yang lebih dekat.
Kami telah menemukan bahwa menggunakan distribusi sederhana ini mengurangi kesalahan prediksi untuk sejumlah set data wajah. Gambar 4 membandingkan fitur yang dipilih dengan dan tanpa itu, di mana ukuran kumpulan objek dalam kedua kasus diatur ke 20.
2.4. Menangani Tag yang Hilang
Masalah persamaan (10) dapat dengan mudah diperluas untuk menangani kasus ketika beberapa landmark tidak ditandai pada beberapa gambar pelatihan (atau kami memiliki ukuran ketidakpastian untuk setiap landmark). Masukkan variabel 
[0, 1] untuk setiap gambar pelatihan i dan setiap tengara j . Instalasi 
nilai 0 menunjukkan bahwa landmark j tidak ditandai dalam gambar ke- i , dan pengaturan 1 menunjukkan bahwa itu ditandai. Maka persamaan (10) dapat direpresentasikan sebagai berikut
dimana 
- matriks diagonal dengan vektor 
di diagonal dan
untuk (13)
Algoritma peningkatan gradien juga harus dimodifikasi untuk memperhitungkan bobot ini. Ini dapat dilakukan dengan hanya menginisialisasi model ensemble dengan nilai rata-rata tertimbang dari target dan menyesuaikan pohon regresi ke residu tertimbang dalam algoritma 1 sebagai berikut
(14)
3. Eksperimen
Basis: Untuk mengevaluasi secara akurat kinerja metode yang kami usulkan, ansambel pohon regresi (ERT), kami membuat dua basis lagi. Yang pertama didasarkan pada pakis acak (random pakis) dengan sifat seleksi acak (EF), dan yang lainnya adalah versi yang lebih maju dari pendekatan ini dengan pemilihan sifat berdasarkan korelasi (EF + CB), yang merupakan implementasi baru kami [2]. Semua parameter diperbaiki untuk ketiga pendekatan.
EF menggunakan implementasi langsung pakis acak sebagai pelemah lemah dalam ansambel dan merupakan yang tercepat untuk pelatihan. Kami menggunakan metode regularisasi yang sama seperti yang disarankan dalam [2] untuk regularisasi pakis.
EF + CB menggunakan metode pemilihan objek berbasis korelasi yang memproyeksikan nilai output, , ke arah acak w dan memilih pasangan tanda (u, v) untuk mana 
memiliki korelasi sampel tertinggi untuk data pelatihan dengan sasaran yang diprediksi 
.
Parameter
Kecuali ditentukan lain, semua percobaan dilakukan dengan pengaturan parameter tetap berikut. Jumlah regresi kuat dalam kaskade adalah T = 10, dan masing-masing terdiri dari K = 500 regressor yang lemah 
. Kedalaman pohon (atau pakis) digunakan untuk mewakili , set sama dengan F = 5. Pada setiap level kaskade, P = 400 piksel dipilih dari gambar. Untuk melatih regressor yang lemah, kami secara acak memilih sepasang piksel P ini sesuai dengan distribusi kami dan memilih ambang acak untuk membuat pemisahan potensial, seperti yang dijelaskan dalam persamaan (9). Pemisahan terbaik dicapai dengan mengulangi proses ini S = 20 kali dan memilih salah satu yang mengoptimalkan tujuan kami. , R = 20 .
2. , Viola & Jones [17]. .
O (TKF). O (NDTKF S), N — , D — . HELEN [12], .
, , HELEN [12], , , . 2330 , 194 . 2000 , .
LFPW [1], 1432 . , 778 216 , , .
Perbandingan
1 . (Active Shape Models) — STASM [14] CompASM [12].
1. HELEN. — . . , . , . .
, , . 3 , , ERT , . , EF + CB . , EF + CB , .
LFPW [1] ( 2). EF + CB , [2]. ( , .) , , .
2. LFPW. 1.
4 (12) , , . λ 0,1 . . 4 .
3. . , , . (12).
, . , . — . ν 1 ( ν = 0.1). . , , , ν = 1. (10 ) . ( .)
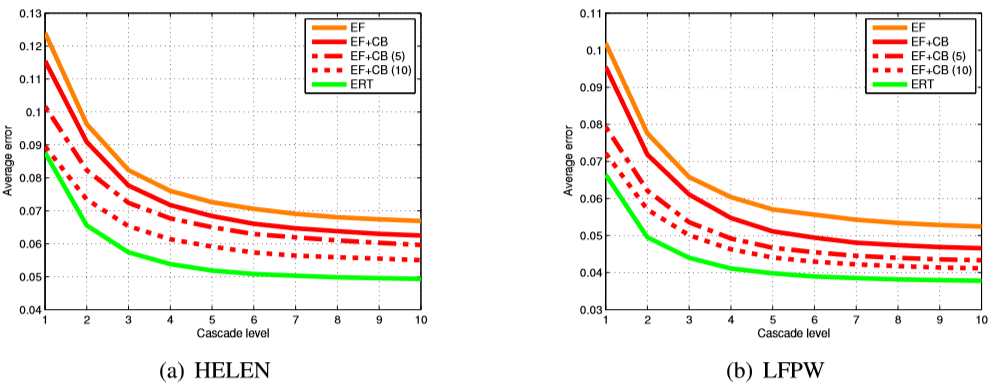
3. HELEN (a) LFPW (b). EF — , EF + CB — , . (5 10), [2]. , (ERT), , , .
4. , . , .
, . , .
4. HELEN . .
, . , , , , .
. . 5 . , , [8, 2] ( 10 × 400 .)
5. .
Data pelatihan
Untuk menguji keefektifan metode kami dalam hal jumlah gambar pelatihan, kami melatih berbagai model dari subset data pelatihan yang berbeda. Tabel 6 merangkum hasil akhir, dan Gambar 5 menunjukkan grafik kesalahan di setiap tingkat kaskade. Menggunakan banyak level regressor sangat berguna ketika kita memiliki banyak contoh pelatihan.
Kami mengulangi percobaan yang sama dengan jumlah total tetap contoh yang diperluas, tetapi mengubah kombinasi bentuk awal yang digunakan untuk membuat contoh pelatihan dari satu contoh wajah yang ditandai dan sejumlah gambar beranotasi yang digunakan untuk mempelajari kaskade (Tabel 7).
Tabel 6. Tingkat kesalahan akhir untuk jumlah contoh pelatihan. Saat membuat data pelatihan untuk mempelajari regresi cascading, setiap gambar wajah yang ditandai menghasilkan 20 contoh pelatihan, menggunakan 20 wajah yang ditandai sebagai asumsi awal tentang bentuk wajah.
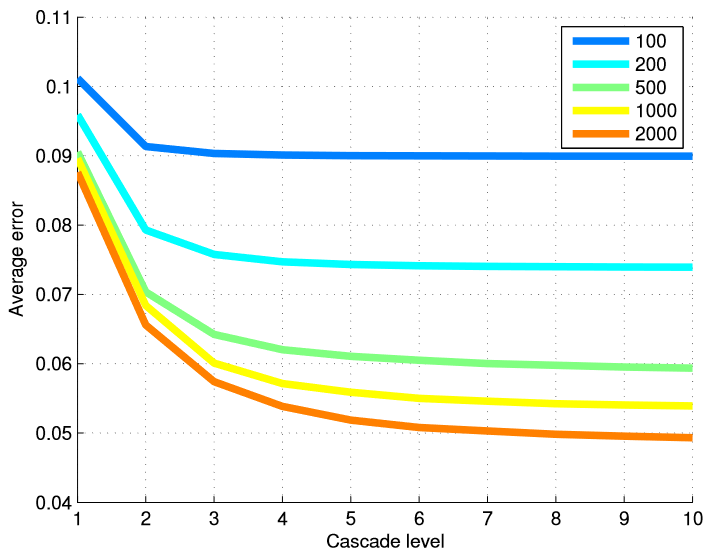
Gambar 5. Kesalahan rata-rata di setiap tingkat kaskade disajikan tergantung pada jumlah contoh pelatihan yang digunakan. Penggunaan banyak level regressor sangat berguna ketika jumlah contoh pelatihan besar.
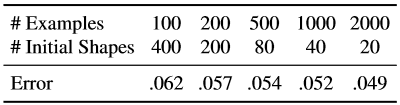
Tabel 7. Di sini jumlah contoh pelatihan efektif diperbaiki, tetapi kami menggunakan berbagai kombinasi jumlah gambar pelatihan dan jumlah formulir awal yang digunakan untuk setiap gambar wajah yang ditandai.
Meningkatkan data pelatihan menggunakan berbagai formulir awal akan memperluas kumpulan data dalam bentuk formulir. Hasil kami menunjukkan bahwa jenis suplemen ini tidak sepenuhnya mengimbangi ketiadaan gambar pelatihan beranotasi. Meskipun tingkat peningkatan diperoleh dengan meningkatkan jumlah gambar pelatihan dengan cepat menurun setelah beberapa ratus gambar pertama.
Anotasi sebagian
Tabel 8 menunjukkan hasil penggunaan data beranotasi sebagian. 200 studi kasus dijelaskan sepenuhnya, dan sisanya hanya sebagian.
Tabel 8. Hasil menggunakan data berlabel sebagian. 200 contoh selalu sepenuhnya beranotasi. Nilai dalam tanda kurung menunjukkan persentase landmark yang diamati.
Hasilnya menunjukkan bahwa kami dapat mencapai peningkatan yang signifikan menggunakan data yang diberi label sebagian. Namun, peningkatan yang ditampilkan mungkin tidak jenuh, karena kita tahu bahwa ukuran dasar dari parameter bentuk jauh lebih rendah daripada ukuran landmark (194 × 2). Akibatnya, ada potensi untuk peningkatan yang lebih signifikan dengan tanda parsial, jika Anda secara eksplisit menggunakan korelasi antara posisi tengara. Harap dicatat bahwa prosedur peningkatan gradien yang dijelaskan dalam artikel ini tidak menggunakan korelasi antara landmark. Masalah ini dapat diselesaikan di pekerjaan mendatang.
4. Kesimpulan
Kami menggambarkan bagaimana ansambel pohon regresi dapat digunakan untuk regresi lokasi landmark wajah dari himpunan bagian dari nilai intensitas yang diekstraksi dari gambar input. Struktur yang disajikan mengurangi kesalahan lebih cepat dari pekerjaan sebelumnya, dan juga dapat memproses tanda parsial atau tidak terdefinisi. Sementara komponen utama dari algoritma kami mempertimbangkan berbagai pengukuran target sebagai variabel independen, kelanjutan alami dari pekerjaan ini adalah penggunaan korelasi parameter bentuk untuk pelatihan yang lebih efektif dan penggunaan label parsial yang lebih baik.
Gambar 6. Hasil akhir dalam database HELEN.
Ucapan Terima Kasih
Pekerjaan ini didanai oleh Swedish Strategic Research Foundation sebagai bagian dari proyek VINST.
Literatur bekas
[1] PN Belhumeur, DW Jacobs, DJ Kriegman, dan N. Kumar. Melokalkan bagian-bagian wajah menggunakan konsensus eksemplar. Dalam CVPR, halaman 545–552, 2011. 1, 5
[2] X. Cao, Y. Wei, F. Wen, dan J. Sun. Perataan wajah dengan regresi bentuk eksplisit. Dalam CVPR, halaman 2887–2894, 2012. 1, 2, 3, 4, 5, 6
[3] TF Cootes, M. Ionita, C. Lindner, dan P. Sauer. Model bentuk yang kuat dan akurat cocok menggunakan voting regresi hutan acak. Dalam ECCV, 2012.1
[4] TF Cootes, CJ Taylor, DH Cooper, dan J. Graham. Model bentuk aktif - pelatihan dan aplikasi mereka. Visi Komputer dan Pemahaman Gambar, 61 (1): 38–59, 1995.1, 2
[5] D. Cristinacce dan TF Cootes. Meningkatkan model bentuk aktif regresi. Dalam BMVC, halaman 79.1–79.10, 2007.1
[6] M. Dantone, J. Gall, G. Fanelli, dan LV Gool. Deteksi fitur wajah real-time menggunakan hutan regresi bersyarat. Dalam CVPR, 2012.1
[7] L. Ding dan AM Mart´ınez. Deteksi rinci wajah dan fitur wajah. Dalam CVPR, 2008.1
[8] P. Dollar, P. Welinder, dan P. Perona. Regresi bertingkat bertingkat. Dalam CVPR, halaman 1078-1085, 2010. 1, 2, 6
[9] GJ Edwards, TF Cootes, dan CJ Taylor. Kemajuan dalam model penampilan aktif. Dalam ICCV, halaman 137–142, 1999. 1, 2
[10] T. Hastie, R. Tibshirani, dan JH Friedman. Unsur-unsur pembelajaran statistik: penambangan data, inferensi, dan prediksi. New York: Springer-Verlag, 2001.2,3
[11] V. Kazemi dan J. Sullivan. Penjajaran wajah dengan pemodelan berbasis bagian. Dalam BMVC, halaman 27.1–27.10, 2011.2
[12] V. Le, J. Brandt, Z. Lin, LD Bourdev, dan TS Huang. Pelokalan fitur wajah interaktif. Dalam [13] L. Liang, R. Xiao, F. Wen, dan J. Sun. Penjajaran wajah melalui pencarian diskriminatif berbasis komponen. Dalam ECCV, halaman 72-85, 2008. 1ECCV, halaman 679- 692, 2012.5
[14] S. Milborrow dan F. Nicolls. Menemukan fitur wajah dengan model bentuk aktif yang diperluas. Dalam ECCV, halaman 504–513, 2008.5
[15] J. Saragih, S. Lucey, dan J. Cohn. Model yang dapat dideformasi pas oleh pergeseran tengara yang teregulasi. Jurnal Internasional Visi Komputer, 91: 200–215, 2010.1
[16] BM Smith dan L. Zhang. Penjajaran wajah bersama dengan model bentuk nonparametrik. Dalam ECCV, halaman 43–56, 2012.1
[17] PA Viola dan MJ Jones. Deteksi wajah real-time yang tangguh. Dalam ICCV, halaman 747, 2001.5
[18] X. Zhao, X. Chai, dan S. Shan. Penjajaran wajah bersama: Menyelamatkan penyelarasan buruk dengan yang baik dengan memasang kembali secara teratur. Dalam ECCV, 2012.1
[19] X. Zhu dan D. Ramanan. Deteksi wajah, estimasi pose, dan pelokalan landmark di alam liar. Dalam CVPR, halaman 2879–2886, 2012.1