Mengapa artikel selanjutnya tentang cara menulis jaringan saraf dari awal? Sayangnya, saya tidak dapat menemukan artikel di mana teori dan kode dijelaskan dari awal hingga model yang berfungsi penuh. Saya segera memperingatkan bahwa akan ada banyak matematika. Saya berasumsi bahwa pembaca akrab dengan dasar-dasar aljabar linier, turunan parsial, dan setidaknya sebagian, dengan teori probabilitas, serta Python dan Numpy. Kami akan berurusan dengan jaringan saraf yang terhubung penuh dan MNIST.
Matematika Bagian 1 (sederhana)
Apa itu lapisan yang terhubung penuh (lapisan FC)? Biasanya mereka mengatakan sesuatu seperti "Lapisan yang sepenuhnya terhubung adalah lapisan, masing-masing neuron yang terhubung ke semua neuron dari lapisan sebelumnya". Hanya tidak jelas apa itu neuron, bagaimana mereka terhubung, terutama dalam kode. Sekarang saya akan mencoba menguraikan ini dengan sebuah contoh. Biarkan ada lapisan 100 neuron. Saya tahu bahwa saya belum menjelaskan apa itu, tetapi mari kita bayangkan bahwa ada 100 neuron dan mereka memiliki input dari mana data dikirim, dan output dari mana mereka memberikan data. Dan gambar hitam-putih 28x28 piksel diumpankan ke input - hanya 784 nilai, jika Anda merentangkannya menjadi vektor. Gambar dapat disebut lapisan input. Kemudian, untuk masing-masing dari 100 neuron untuk terhubung dengan setiap "neuron" atau, jika Anda suka, nilai dari lapisan sebelumnya (yaitu, gambar), perlu bahwa masing-masing dari 100 neuron menerima 784 nilai dari gambar asli. Sebagai contoh, untuk masing-masing dari 100 neuron itu akan cukup untuk melipatgandakan nilai 784 gambar dengan sekitar 784 angka dan menambahkannya bersama-sama, sebagai hasilnya, satu angka keluar. Artinya, ini adalah neuron:
$$ menampilkan $$ \ teks {Output neuron} = \ teks {beberapa angka} _ {1} \ cdot \ teks {nilai gambar} _1 ~ + \\ + ~ ... ~ + ~ \ teks {some- angka itu} _ {784} \ cdot \ text {nilai gambar} _ {784} $$ menampilkan $$
Kemudian ternyata setiap neuron memiliki 784 angka, dan semua angka ini: (jumlah neuron pada lapisan ini) x (jumlah neuron pada lapisan sebelumnya) =
$ inline $ 100 \ times784 $ inline $ = 78.400 digit. Angka-angka ini biasa disebut layer weight. Setiap neuron akan memberikan jumlahnya dan sebagai hasilnya kita mendapatkan vektor 100 dimensi, dan pada kenyataannya kita dapat menulis bahwa vektor 100 dimensi ini diperoleh dengan mengalikan vektor 784 dimensi (gambar asli kita) dengan ukuran matriks ukuran
$ inline $ 100 \ times784 $ inline $ :
$$ tampilkan $$ \ boldsymbol {x} ^ {100} = W_ {100 \ times784} \ cdot \ boldsymbol {x} ^ {784} $$ tampilkan $$
Selanjutnya, 100 nomor yang dihasilkan diteruskan, ke fungsi aktivasi - beberapa fungsi non-linear - yang mempengaruhi masing-masing nomor secara terpisah. Misalnya sigmoid, singgung hiperbolik, ReLU dan lainnya. Fungsi aktivasi tentu non-linear, jika tidak, jaringan saraf akan belajar hanya transformasi sederhana.
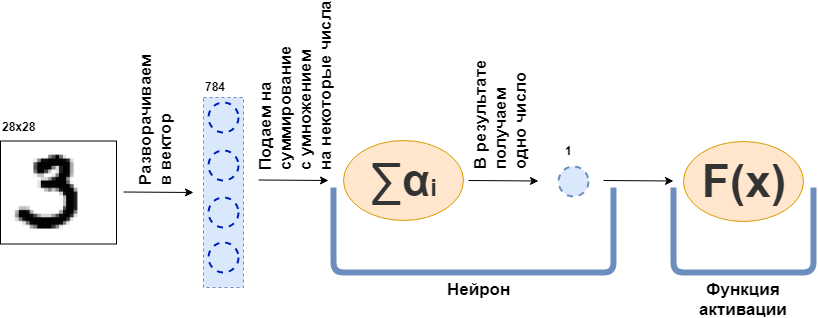
Kemudian, data yang dihasilkan diumpankan kembali ke lapisan yang sepenuhnya terhubung, tetapi dengan jumlah neuron yang berbeda, dan lagi ke fungsi aktivasi. Ini terjadi beberapa kali. Lapisan terakhir dari jaringan adalah lapisan yang menghasilkan jawaban. Dalam hal ini, jawabannya adalah informasi tentang nomor dalam gambar.
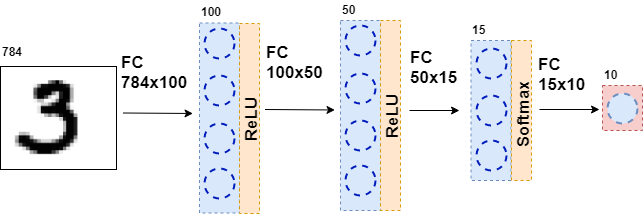
Selama pelatihan jaringan, kita perlu tahu angka apa yang ditunjukkan pada gambar. Yaitu, bahwa dataset ditandai. Kemudian Anda dapat menggunakan elemen lain - fungsi kesalahan. Dia melihat respon dari jaringan saraf dan membandingkannya dengan jawaban yang sebenarnya. Berkat ini, jaringan saraf sedang belajar.
Pernyataan umum masalah
Seluruh dataset adalah tensor besar (kami akan memanggil array data multidimensi tensor)
$ sebaris $ \ boldsymbol {X} = \ kiri [\ boldsymbol {x} _1, \ boldsymbol {x} _2, \ ldots, \ boldsymbol {x} _n \ kanan] $ inline $ dimana
$ inline $ \ boldsymbol {x} _i $ inline $ - Objek ke-i, misalnya, gambar, yang juga merupakan tensor. Untuk setiap objek ada
$ inline $ y_i $ inline $ - jawaban yang benar pada objek ke-i. Dalam hal ini, jaringan saraf dapat direpresentasikan sebagai beberapa fungsi yang mengambil objek sebagai input dan memberikan beberapa jawaban padanya:
$$ menampilkan $$ F (\ boldsymbol {x} _i) = \ hat {y} _i $$ menampilkan $$
Sekarang mari kita lihat lebih dekat fungsi
$ inline $ F (\ boldsymbol {x} _i) $ inline $ . Karena jaringan saraf terdiri dari lapisan, setiap lapisan individu adalah fungsi. Dan itu artinya
$$ menampilkan $$ F (\ boldsymbol {x} _i) = f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i)))) = \ hat {y} _i $$ display $ $
Artinya, pada fungsi paling pertama - lapisan pertama - gambar disajikan dalam bentuk tensor. Fungsi
$ inline $ f_1 $ inline $ memberikan beberapa jawaban - juga tensor, tetapi dari dimensi yang berbeda. Tensor ini akan disebut representasi internal. Sekarang representasi internal ini diumpankan ke input fungsi
$ inline $ f_2 $ inline $ , yang memberikan representasi internal. Begitu seterusnya, hingga fungsinya
$ inline $ f_k $ inline $ - lapisan terakhir - tidak akan memberikan jawaban
$ inline $ \ hat {y} _i $ inline $ .
Sekarang, tugasnya adalah melatih jaringan - untuk membuat jawaban jaringan cocok dengan jawaban yang benar. Pertama, Anda perlu mengukur seberapa salah jaringan saraf itu. Mengukur ini adalah fungsi kesalahan.
$ inline $ L (\ hat {y} _i, y_i) $ inline $ . Dan kami memberlakukan batasan:
1.
$ inline $ \ hat {y} _i \ xrightarrow {} y_i \ Rightarrow L (\ hat {y} _i, y_i) \ xrightarrow {} 0 $ inline $
2.
$ inline $ \ exist ~ dL (\ hat {y} _i, y_i) $ inline $
3.
$ inline $ L (\ hat {y} _i, y_i) \ geq 0 $ inline $
Pembatasan 2 dikenakan pada semua fungsi lapisan
$ inline $ f_j $ inline $ - biarkan semuanya dibedakan.
Selain itu, pada kenyataannya (saya tidak menyebutkan ini) beberapa fungsi ini tergantung pada parameter - bobot jaringan saraf -
$ inline $ f_j (\ boldsymbol {x} _i | \ boldsymbol {\ omega} _j) $ inline $ . Dan seluruh idenya adalah untuk mengambil bobot tersebut sehingga
$ inline $ \ hat {y} _i $ inline $ bertepatan dengan
$ inline $ y_i $ inline $ pada semua objek dataset. Saya perhatikan bahwa tidak semua fungsi memiliki bobot.
Jadi, di mana kita berhenti? Semua fungsi jaringan saraf dapat dibedakan, fungsi kesalahan juga dapat dibedakan. Ingat salah satu sifat gradien - tunjukkan arah pertumbuhan fungsi. Kami menggunakan ini, pembatasan 1 dan 3, fakta itu
$$ menampilkan $$ L (F (\ boldsymbol {x} _i)) = L (f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i)))))) = L (\ hat {y} _i) $$ tampilkan $$
dan fakta bahwa saya dapat mempertimbangkan turunan parsial dan turunan dari fungsi yang kompleks. Sekarang ada semua yang Anda butuhkan untuk menghitung
$$ tampilkan $$ \ frac {\ partial L (F (\ boldsymbol {x} _i))} {\ partial \ boldsymbol {\ omega_j}} $$ tampilkan $$
untuk i dan j. Derivatif parsial ini menunjukkan arah perubahan
$ inline $ \ boldsymbol {\ omega_j} $ inline $ untuk memperbesar
$ inline $ L $ inline $ . Untuk mengurangi Anda perlu mengambil langkah ke samping
$ inline $ - \ frac {\ partial L (F (\ boldsymbol {x} _i))} {\ partial \ boldsymbol {\ omega_j}} $ inline $ tidak ada yang rumit.
Jadi proses pelatihan jaringan dibangun sebagai berikut: beberapa kali dalam satu siklus kita melewati seluruh dataset (ini disebut era), untuk setiap objek dataset yang kita pertimbangkan
$ inline $ L (\ hat {y} _i, y_i) $ inline $ (ini disebut forward pass) dan pertimbangkan turunan parsial
$ inline $ \ partial L $ inline $ untuk semua bobot
$ inline $ \ boldsymbol {\ omega_j} $ inline $ , lalu perbarui bobot (ini disebut backward pass).
Saya perhatikan bahwa saya belum memperkenalkan fungsi dan lapisan tertentu. Jika pada tahap ini tidak jelas apa yang harus dilakukan dengan semua ini, saya usulkan untuk terus membaca - akan ada lebih banyak matematika, tetapi sekarang akan dilanjutkan dengan contoh.
Matematika Bagian 2 (sulit)
Fungsi kesalahan
Saya akan mulai dari akhir dan menampilkan fungsi kesalahan untuk masalah klasifikasi. Untuk masalah regresi, derivasi dari fungsi kesalahan dijelaskan dengan baik dalam buku "Belajar Dalam. Perendaman dalam dunia jaringan saraf. "
Untuk kesederhanaan, ada jaringan saraf (NN) yang memisahkan foto kucing dari foto anjing, dan ada satu set foto kucing dan anjing yang ada jawaban yang benar
$ inline $ y_ {true} $ inline $ .
$$ menampilkan $$ NN (gambar | \ Omega) = y_ {pred} $$ menampilkan $$
Semua yang akan saya lakukan selanjutnya sangat mirip dengan metode kemungkinan maksimum. Oleh karena itu, tugas utama adalah menemukan fungsi kemungkinan. Jika kita menghilangkan detail, maka fungsi yang membandingkan prediksi jaringan saraf dan jawaban yang benar, dan jika mereka bertepatan, memberikan nilai yang besar, jika tidak, sebaliknya. Peluang jawaban yang benar muncul di benak Anda dengan parameter yang diberikan:
$$ menampilkan $$ p (y_ {pred} = y_ {true} | \ Omega) $$ menampilkan $$
Dan sekarang kita akan membuat tipuan, yang, sepertinya, tidak mengikuti dari mana saja. Biarkan jaringan saraf memberikan jawaban dalam bentuk vektor dua dimensi, jumlah nilai-nilainya adalah 1. Elemen pertama dari vektor ini dapat disebut ukuran keyakinan bahwa kucing ada di foto, dan elemen kedua adalah ukuran keyakinan bahwa anjing ada di foto. Ya, ini hampir merupakan probabilitas!
$$ menampilkan $$ NN (gambar | \ Omega) = \ kiri [\ mulai {matrix} p_0 \\ p_1 \\ end {matrix} \ kanan] $$ menampilkan $$
Sekarang fungsi likelihood dapat ditulis ulang sebagai:
$$ menampilkan $$ p (y_ {pred} = y_ {true} | \ Omega) = p_ \ Omega (y_ {pred}) ^ t_ {0} * (1 - p_ \ Omega (y_ {pred})) ^ t_ {1} = \\ p_0 ^ {t_0} * p_1 ^ {t_1} $$ menampilkan $$
Dimana
$ inline $ t_0, t_1 $ inline $ label dari kelas yang benar, misalnya, jika
$ inline $ y_ {true} = cat $ inline $ lalu
$ inline $ t_0 == 1, t_1 == $ $ inline $ jika
$ inline $ y_ {true} = dog $ inline $ lalu
$ inline $ t_0 == 0, t_1 == 1 $ inline $ . Dengan demikian, probabilitas kelas yang seharusnya diprediksi oleh jaringan saraf (tetapi tidak harus diprediksi olehnya) selalu dipertimbangkan. Sekarang ini dapat digeneralisasi ke sejumlah kelas (misalnya, kelas m):
$$ menampilkan $$ p (y_ {pred} = y_ {true} | \ Omega) = \ prod_0 ^ m p_i ^ {t_i} $$ menampilkan $$
Namun, dalam dataset apa pun ada banyak objek (misalnya, objek N). Saya ingin jaringan saraf untuk memberikan jawaban yang benar pada masing-masing atau sebagian besar objek. Dan untuk ini, Anda perlu mengalikan hasil rumus di atas untuk setiap objek dari dataset.
$$ tampilkan $$ MaximumLikelyhood = \ prod_ {j = 0} ^ N \ prod_ {i = 0} ^ m p_ {i, j} ^ {t_ {i, j}} $$ display $$
Untuk mendapatkan hasil yang baik, fungsi ini perlu dimaksimalkan. Tapi, pertama, lebih curam untuk meminimalkan, karena kami memiliki keturunan gradien stokastik dan semua roti untuk itu - hanya menetapkan minus, dan kedua, sulit untuk bekerja dengan pekerjaan besar - itu logaritma.
$$ tampilkan $$ CrossEntropyLoss = - \ jumlah \ limit_ {j = 0} ^ {N} \ jumlah \ limit_ {i = 0} ^ {m} t_ {i, j} \ cdot \ log (p_ {i, j }) $$ menampilkan $$
Hebat! Hasilnya adalah entropi silang atau, dalam kasus biner, logloss. Fungsi ini mudah untuk dihitung dan bahkan lebih mudah untuk dibedakan:
$$ tampilkan $$ \ frac {\ partial CrossEntropyLoss} {\ partial p_j} = - \ frac {\ boldsymbol {t_j}} {\ boldsymbol {p_ {j}}} $$ display $$
Anda perlu membedakan untuk algoritma backpropagation. Saya perhatikan bahwa fungsi kesalahan tidak mengubah dimensi vektor. Jika, seperti dalam kasus MNIST, outputnya adalah vektor jawaban 10-dimensi, maka ketika menghitung turunannya, kita mendapatkan vektor turunan 10-dimensi. Hal lain yang menarik adalah bahwa hanya satu elemen turunan tidak akan nol, di mana
$ inline $ t_ {i, j} \ neq 0 $ inline $ , yaitu, dengan jawaban yang benar. Dan semakin kecil kemungkinan jawaban yang benar diprediksi oleh jaringan saraf pada objek yang diberikan, semakin banyak fungsi kesalahan di dalamnya.
Fitur aktivasi
Pada output dari setiap lapisan yang terhubung penuh dari jaringan saraf, fungsi aktivasi nonlinier harus ada. Tanpa itu, tidak mungkin untuk melatih jaringan saraf yang bermakna. Ke depan, lapisan jaringan neural yang terhubung sepenuhnya hanyalah perkalian dari data input dengan matriks bobot. Dalam aljabar linier, ini disebut peta linier - fungsi linier. Kombinasi fungsi linier juga merupakan fungsi linier. Tetapi ini berarti bahwa fungsi seperti itu hanya dapat mendekati fungsi linear. Sayangnya, ini bukan mengapa jaringan saraf diperlukan.
Softmax
Biasanya fungsi ini digunakan pada lapisan terakhir jaringan, karena ia mengubah vektor dari lapisan terakhir menjadi vektor "probabilitas": setiap elemen vektor terletak dari 0 hingga 1 dan jumlahnya adalah 1. Tidak mengubah dimensi vektor.
$$ menampilkan $$ Softmax_i = \ frac {e ^ {x_i}} {\ jumlah \ limit_ {j} e ^ {x_j}} $$ menampilkan $$
Sekarang mari kita beralih ke pencarian turunan. Sejak
$ inline $ \ boldsymbol {x} $ inline $ Merupakan vektor, dan semua elemennya selalu ada dalam penyebutnya, maka ketika mengambil turunannya kita mendapatkan Jacobian:
$$ menampilkan $$ J_ {Softmax} = \ mulai {kas} x_i - x_i \ cdot x_j, i = j \\ - x_i \ cdot x_j, i \ neq j \ end {kas} $$ menampilkan $$
Sekarang tentang backpropagation. Vektor turunan berasal dari lapisan sebelumnya (biasanya ini adalah fungsi kesalahan)
$ inline $ \ boldsymbol {dz} $ inline $ . Dalam kasus
$ inline $ \ boldsymbol {dz} $ inline $ berasal dari fungsi kesalahan pada mnist,
$ inline $ \ boldsymbol {dz} $ inline $ - Vektor 10 dimensi. Kemudian Jacobian memiliki dimensi 10x10. Untuk mendapatkan
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ , yang melangkah lebih jauh ke lapisan sebelumnya (jangan lupa bahwa kita pergi dari ujung ke awal jaringan ketika kesalahan menyebar kembali), kita perlu memperbanyak
$ inline $ \ boldsymbol {dz} $ inline $ pada
$ inline $ J_ {Softmax} $ inline $ (baris per kolom):
$$ menampilkan $$ dz_ {baru} = \ boldsymbol {dz} \ kali J_ {Softmax} $$ menampilkan $$
Pada output, kita mendapatkan vektor turunan 10 dimensi
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ .
Relu
$$ menampilkan $$ ReLU (x) = \ mulai {kas} x, x> 0 \\ 0, x <0 \ akhir {kas} $$ menampilkan $$
ReLU mulai digunakan secara besar-besaran setelah 2011, ketika artikel "Deep Sparse Rectifier Neural Networks" diterbitkan. Namun, fungsi seperti itu sebelumnya diketahui. Konsep "kekuatan aktivasi" berlaku untuk ReLU (untuk lebih jelasnya, lihat buku "Deep Learning. Immersion in the World of Neural Networks"). Tetapi fitur utama yang membuat ReLU lebih menarik daripada fungsi aktivasi lainnya adalah perhitungan turunannya yang sederhana:
$$ menampilkan $$ d (ReLU (x)) = \ mulai {kas} 1, x> 0 \\ 0, x <0 \ akhir {kas} $$ menampilkan $$
Dengan demikian, ReLU secara komputasi lebih efisien daripada fungsi aktivasi lainnya (sigmoid, hiperbolik tangen, dll.).
Lapisan sepenuhnya terhubung
Sekarang saatnya untuk membahas lapisan yang terhubung sepenuhnya. Yang paling penting dari semua yang lain, karena pada lapisan inilah semua bobot berada, yang harus disesuaikan agar jaringan saraf dapat bekerja dengan baik. Lapisan yang terhubung sepenuhnya hanyalah matriks berat:
$$ display $$ W = | w_ {i, j} | $$ display $$
Representasi internal baru diperoleh ketika matriks bobot dikalikan dengan kolom input:
$$ menampilkan $$ \ boldsymbol {x} _ {baru} = W \ cdot \ boldsymbol {x} $$ menampilkan $$
Dimana
$ inline $ \ boldsymbol {x} $ inline $ memiliki ukuran
$ inline $ input \ _shape $ inline $ , dan
$ inline $ x_ {new} $ inline $ -
$ inline $ output \ _shape $ inline $ . Sebagai contoh
$ inline $ \ boldsymbol {x} $ inline $ - Vektor 784 dimensi, dan
$ inline $ \ boldsymbol {x} _ {new} $ inline $ Merupakan vektor 100 dimensi, maka matriks W memiliki ukuran 100x784. Ternyata pada layer ini adalah 100x784 = 78.400 bobot.
Dengan propagasi belakang kesalahan, kita perlu mengambil turunan sehubungan dengan setiap bobot matriks ini. Sederhanakan masalahnya dan ikuti turunannya saja
$ inline $ w_ {1,1} $ inline $ . Saat mengalikan matriks dan vektor, elemen pertama dari vektor baru
$ inline $ \ boldsymbol {x} _ {new} $ inline $ sama dengan
$ sebaris $ x_ {baru ~ 1} = w_ {1,1} \ cdot x_1 + ... + w_ {1,784} \ cdot x_ {784} $ sebaris $ , dan turunannya
$ sebaris $ x_ {baru ~ 1} $ sebaris $ oleh
$ inline $ w_ {1,1} $ inline $ akan sederhana
$ inline $ x_1 $ inline $ , Anda hanya perlu mengambil turunan dari jumlah di atas. Demikian pula yang terjadi untuk semua bobot lainnya. Tapi ini bukan algoritma propagasi kesalahan kembali, asalkan itu hanya matriks turunan. Anda harus ingat bahwa dari lapisan berikutnya ke ini (kesalahan beranjak dari ujung ke awal) menghasilkan vektor gradien 100-dimensi
$ inline $ d \ boldsymbol {z} $ inline $ . Elemen pertama dari vektor ini
$ inline $ dz_1 $ inline $ akan dikalikan dengan semua elemen dari matriks turunan yang "berpartisipasi" dalam penciptaan
$ sebaris $ x_ {baru ~ 1} $ sebaris $ , mis. aktif
$ sebaris $ x_1, x_2, ..., x_ {784} $ sebaris $ . Begitu pula dengan elemen yang tersisa. Jika Anda menerjemahkan ini ke dalam bahasa aljabar linier, maka itu ditulis seperti ini:
$$ menampilkan $$ \ frac {\ partial L} {\ partial W} = (d \ boldsymbol {z}, ~ dW) = \ kiri (\ begin {matrix} dz_ {1} \ cdot \ boldsymbol {x} \ \ ... \\ dz_ {100} \ cdot \ boldsymbol {x} \ end {matrix} \ kanan) _ {100} $$ tampilkan $$
Outputnya adalah matriks 100x784.
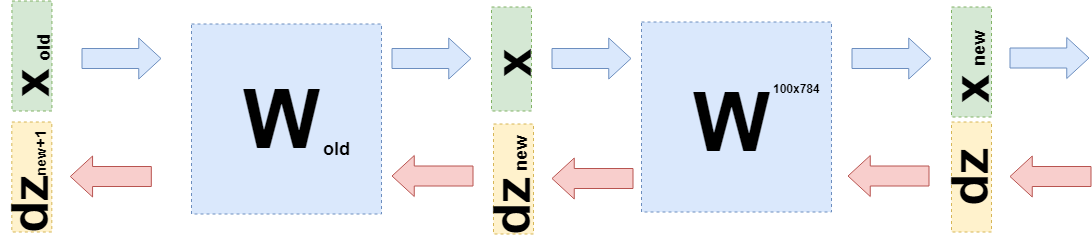
Sekarang Anda perlu memahami apa yang harus ditransfer ke lapisan sebelumnya. Untuk ini dan untuk pemahaman yang lebih baik tentang apa yang terjadi sekarang, saya ingin menuliskan apa yang terjadi ketika mengambil turunan pada lapisan ini dalam bahasa yang sedikit berbeda, untuk menjauh dari spesifik "apa yang dikalikan dengan" ke fungsi (lagi).
Ketika saya ingin menyesuaikan bobot, saya ingin mengambil turunan dari fungsi kesalahan untuk bobot ini:
$ inline $ \ frac {\ partial L} {\ partial W} $ inline $ . Itu ditunjukkan di atas cara mengambil turunan dari fungsi kesalahan dan fungsi aktivasi. Oleh karena itu, kita dapat mempertimbangkan kasus seperti itu (dalam bahasa Indonesia)
$ inline $ d \ boldsymbol {z} $ inline $ semua turunan dari fungsi kesalahan dan fungsi aktivasi sudah ada):
$$ menampilkan $$ \ frac {\ partial L} {\ partial W} = d \ boldsymbol {z} \ cdot \ frac {\ partial \ boldsymbol {x} _ {baru} (W)} {\ partial W} $ $ display $$
Ini bisa dilakukan, karena bisa Anda pertimbangkan
$ inline $ \ boldsymbol {x} _ {new} $ inline $ sebagai fungsi dari W:
$ inline $ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $ inline $ .
Anda dapat menggantinya dengan formula di atas:
$$ menampilkan $$ \ frac {\ partial L} {\ partial W} = d \ boldsymbol {z} \ cdot \ frac {\ partial W \ cdot \ boldsymbol {x}} {\ partial W} = d \ boldsymbol { z} \ cdot E \ cdot \ boldsymbol {x} $$ menampilkan $$
Di mana E adalah matriks yang terdiri dari unit (BUKAN matriks unit).
Sekarang ketika Anda perlu mengambil turunan dari lapisan sebelumnya (bahkan jika untuk kesederhanaan perhitungan itu juga akan menjadi lapisan yang terhubung penuh, tetapi dalam kasus umum itu tidak mengubah apa pun), maka Anda perlu mempertimbangkan
$ inline $ \ boldsymbol {x} $ inline $ sebagai fungsi dari layer sebelumnya
$ inline $ \ boldsymbol {x} (W_ {old}) $ inline $ :
$$ tampilan $$ \ begin {collected} \ frac {\ partial L} {\ partial W_ {old}} = d \ boldsymbol {z} \ cdot \ frac {\ partial \ boldsymbol {x} _ {baru} (W )} {\ partial W_ {old}} = d \ boldsymbol {z} \ cdot \ frac {\ partial W \ cdot \ boldsymbol {x} (W_ {old})} {\ partial W_ {old}} = \\ = d \ boldsymbol {z} \ cdot \ frac {\ partial W \ cdot W_ {old} \ cdot \ boldsymbol {x} _ {old}} {\ partial W_ {old}} = d \ boldsymbol {z} \ cdot W \ cdot E \ cdot \ boldsymbol {x} _ {old} = \\ = d \ boldsymbol {z} _ {baru} \ cdot E \ cdot \ boldsymbol {x} _ {old} \ end {berkumpul} $$ tampilkan $$
Tepat
$ inline $ d \ boldsymbol {z} _ {new} = d \ boldsymbol {z} \ cdot W $ inline $ dan Anda perlu mengirim ke lapisan sebelumnya.
Kode
Artikel ini terutama bertujuan menjelaskan matematika jaringan saraf. Saya akan mencurahkan sedikit waktu untuk kode.
Ini adalah contoh implementasi dari fungsi kesalahan:
class CrossEntropy: def forward(self, y_true, y_hat): self.y_hat = y_hat self.y_true = y_true self.loss = -np.sum(self.y_true * np.log(y_hat)) return self.loss def backward(self): dz = -self.y_true / self.y_hat return dz
Kelas memiliki metode untuk lulus langsung dan mundur. Pada saat pass langsung, instance kelas menyimpan data di dalam layer, dan pada saat pass kembali itu menggunakan mereka untuk menghitung gradien. Lapisan yang tersisa dibangun dengan cara yang sama. Berkat ini, menjadi mungkin untuk menulis saraf yang terhubung sepenuhnya dalam gaya ini:
class MnistNet: def __init__(self): self.d1_layer = Dense(784, 100) self.a1_layer = ReLu() self.drop1_layer = Dropout(0.5) self.d2_layer = Dense(100, 50) self.a2_layer = ReLu() self.drop2_layer = Dropout(0.25) self.d3_layer = Dense(50, 10) self.a3_layer = Softmax() def forward(self, x, train=True): ... def backward(self, dz, learning_rate=0.01, mini_batch=True, update=False, len_mini_batch=None): ...
Kode lengkap dapat ditemukan di
sini .
Saya juga menyarankan untuk mempelajari
artikel ini
di Habré .
Kesimpulan
Saya harap saya dapat menjelaskan dan menunjukkan bahwa matematika yang cukup sederhana ada di belakang jaringan saraf dan ini sama sekali tidak menakutkan. Namun demikian, untuk pemahaman yang lebih dalam, ada baiknya mencoba menulis "sepeda" Anda sendiri. Koreksi dan saran dengan senang hati dibaca di komentar.