Jaringan saraf dan pembelajaran mendalam, bab 3, bagian 3: bagaimana memilih hyperparameter jaringan saraf?

Sejauh ini, saya belum menjelaskan bagaimana saya memilih nilai-nilai hyperparameters - kecepatan belajar η, parameter regularisasi λ, dan sebagainya. Saya hanya memberi nilai kerja yang bagus. Dalam praktiknya, ketika Anda menggunakan jaringan saraf untuk menyerang suatu masalah, mungkin sulit untuk menemukan hiperparameter yang baik. Bayangkan, misalnya, bahwa kita baru saja diberitahu tentang masalah MNIST, dan kita mulai mengatasinya, tidak tahu apa-apa tentang nilai-nilai hiperparameter yang sesuai. Misalkan kita beruntung secara kebetulan, dan dalam percobaan pertama kita memilih banyak hiperparameter seperti yang sudah kita lakukan dalam bab ini: 30 neuron tersembunyi, ukuran paket-mini 10, pelatihan untuk 30 era, dan menggunakan cross entropy. Namun, kami memilih tingkat pembelajaran η = 10.0, dan parameter regularisasi λ = 1000.0. Dan inilah yang saya lihat dengan berlari seperti itu:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 1030 / 10000 Epoch 1 training complete Accuracy on evaluation data: 990 / 10000 Epoch 2 training complete Accuracy on evaluation data: 1009 / 10000 ... Epoch 27 training complete Accuracy on evaluation data: 1009 / 10000 Epoch 28 training complete Accuracy on evaluation data: 983 / 10000 Epoch 29 training complete Accuracy on evaluation data: 967 / 10000 

Klasifikasi kami tidak berfungsi lebih baik daripada pengambilan sampel acak! Jaringan kami berfungsi sebagai penghasil derau acak!

"Ya, itu mudah diperbaiki," Anda bisa mengatakan, "kurangi saja hiperparameter seperti kecepatan belajar dan regularisasi." Sayangnya, apriori Anda tidak memiliki informasi tentang apa sebenarnya hyperparameter ini yang perlu Anda sesuaikan. Mungkin masalah utamanya adalah bahwa 30 neuron tersembunyi kita tidak akan pernah berfungsi, terlepas dari bagaimana hiperparameter lainnya dipilih? Mungkin kita membutuhkan setidaknya 100 neuron tersembunyi? Atau 300? Atau banyak lapisan tersembunyi? Atau pendekatan berbeda untuk pengkodean keluaran? Mungkin jaringan kita sedang belajar, tetapi kita perlu melatihnya lebih banyak era? Mungkin ukuran paket mini terlalu kecil? Mungkin kita akan melakukan lebih baik jika kita kembali ke fungsi nilai kuadrat? Mungkin kita perlu mencoba pendekatan berbeda untuk menginisialisasi bobot? Dan seterusnya dan seterusnya. Dalam ruang hiperparameter mudah hilang. Dan ini benar-benar dapat membawa banyak ketidaknyamanan jika jaringan Anda sangat besar, atau menggunakan sejumlah besar data pelatihan, dan Anda dapat melatihnya selama berjam-jam, berhari-hari atau berminggu-minggu tanpa menerima hasil. Dalam situasi seperti itu, kepercayaan diri Anda mulai berlalu. Mungkin jaringan saraf adalah pendekatan yang salah untuk menyelesaikan masalah Anda? Mungkin Anda berhenti dan melakukan perlebahan?

Pada bagian ini, saya akan menjelaskan beberapa pendekatan heuristik yang dapat Anda gunakan untuk mengonfigurasi hyperparameters dalam jaringan saraf. Tujuannya adalah untuk membantu Anda mengetahui alur kerja yang memungkinkan Anda mengkonfigurasi hyperparameters dengan cukup baik. Tentu saja, saya tidak bisa membahas seluruh topik optimasi hiperparameter. Ini adalah area yang sangat luas, dan ini bukan masalah yang dapat diselesaikan sepenuhnya, atau sesuai dengan strategi yang tepat untuk penyelesaian yang ada kesepakatan universal. Selalu ada kesempatan untuk mencoba beberapa trik lain untuk memeras hasil tambahan dari jaringan saraf Anda. Tetapi heuristik di bagian ini harus memberi Anda titik awal.

Strategi umum

Ketika menggunakan jaringan saraf untuk menyerang masalah baru, kesulitan pertama adalah mendapatkan hasil non-sepele dari jaringan, yaitu, melebihi probabilitas acak. Ini bisa sangat sulit, terutama ketika Anda dihadapkan dengan kelas tugas baru. Mari kita lihat beberapa strategi yang dapat digunakan untuk kesulitan semacam ini.

Misalkan, misalnya, bahwa Anda adalah orang pertama yang menyerang tugas MNIST. Anda mulai dengan antusiasme yang besar, tetapi kegagalan total jaringan pertama Anda sedikit mengecewakan, seperti dijelaskan dalam contoh di atas. Maka Anda perlu membongkar masalah di beberapa bagian. Anda harus menyingkirkan semua pelatihan dan gambar pendukung, kecuali untuk gambar nol dan satu. Kemudian cobalah untuk melatih jaringan untuk membedakan 0 dari 1. Tugas ini tidak hanya pada dasarnya lebih mudah daripada membedakan semua sepuluh digit, itu juga mengurangi jumlah data pelatihan sebesar 80%, mempercepat pembelajaran sebanyak 5 kali. Ini memungkinkan Anda untuk melakukan eksperimen lebih cepat, dan memberi Anda kesempatan untuk dengan cepat memahami cara membuat jaringan yang baik.

Eksperimen dapat dipercepat lebih lanjut dengan mengurangi jaringan ke ukuran minimum yang mungkin dilatih secara bermakna. Jika Anda berpikir bahwa jaringan [784, 10] sangat mungkin untuk dapat mengklasifikasikan digit MNIST lebih baik daripada sampel acak, maka mulailah bereksperimen dengannya. Ini akan menjadi jauh lebih cepat daripada melatih [784, 30, 10], dan Anda sudah bisa tumbuh nantinya.

Percepatan lain dari percobaan dapat diperoleh dengan meningkatkan frekuensi pelacakan. Dalam program network2.py, kami memantau kualitas pekerjaan di akhir setiap era. Memproses 50.000 gambar per era, kita harus menunggu waktu yang cukup lama - sekitar 10 detik per era di laptop saya ketika mempelajari jaringan [784, 30, 10] - sebelum mendapatkan umpan balik tentang kualitas pembelajaran jaringan. Tentu saja, sepuluh detik tidak terlalu lama, tetapi jika Anda ingin mencoba beberapa puluh hiperparameter yang berbeda, itu mulai mengganggu, dan jika Anda ingin mencoba ratusan atau ribuan opsi, itu hanya menghancurkan. Umpan balik dapat diterima lebih cepat dengan melacak akurasi konfirmasi lebih sering, misalnya, setiap 1000 gambar pelatihan. Selain itu, alih-alih menggunakan set lengkap 10.000 gambar konfirmasi, kita bisa mendapatkan perkiraan lebih cepat menggunakan hanya 100 gambar konfirmasi. Hal utama adalah bahwa jaringan melihat gambar yang cukup untuk benar-benar belajar, dan untuk mendapatkan perkiraan efektivitas yang cukup baik. Tentu saja, network2.py kami belum menyediakan pelacakan seperti itu. Tetapi sebagai penopang untuk mencapai efek ini untuk tujuan ilustrasi, kami memotong data pelatihan kami ke 1000 gambar MNIST pertama. Mari kita coba melihat apa yang terjadi (untuk kesederhanaan kode, saya tidak menggunakan gagasan hanya menyisakan gambar 0 dan 1 - ini juga dapat diwujudkan dengan sedikit usaha lebih).

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 ... 

Kami masih mendapatkan noise murni, tetapi kami memiliki keuntungan besar: umpan balik diperbarui dalam sepersekian detik, dan tidak setiap sepuluh detik. Ini berarti Anda dapat bereksperimen lebih cepat dengan pemilihan hiperparameter, atau bahkan bereksperimen dengan banyak hiperparameter yang berbeda hampir secara bersamaan.

Pada contoh di atas, saya meninggalkan nilai λ sama dengan 1000.0, seperti sebelumnya. Tetapi karena kita mengubah jumlah contoh pelatihan, kita perlu mengubah λ sehingga melemahnya bobot adalah sama. Ini berarti bahwa kami mengubah λ sebesar 20.0. Dalam hal ini, yang berikut ini akan berubah:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 12 / 100 Epoch 1 training complete Accuracy on evaluation data: 14 / 100 Epoch 2 training complete Accuracy on evaluation data: 25 / 100 Epoch 3 training complete Accuracy on evaluation data: 18 / 100 ... 

Ya! Kami punya sinyal. Tidak terlalu bagus, tapi ada. Ini sudah bisa diambil sebagai titik awal, dan ubah hyperparameter untuk mencoba mendapatkan peningkatan lebih lanjut. Misalkan kita memutuskan bahwa kita perlu meningkatkan kecepatan belajar (seperti yang mungkin Anda pahami, kami memutuskan secara tidak benar, untuk alasan yang akan kami diskusikan nanti, tetapi mari kita coba lakukan ini sekarang). Untuk menguji tebakan kami, kami memutar η ke 100.0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 Epoch 3 training complete Accuracy on evaluation data: 10 / 100 ... 

Semuanya buruk! Rupanya, dugaan kami salah, dan masalahnya bukan pada nilai yang sangat rendah dari kecepatan belajar. Kami mencoba mengencangkan η menjadi nilai kecil 1,0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 62 / 100 Epoch 1 training complete Accuracy on evaluation data: 42 / 100 Epoch 2 training complete Accuracy on evaluation data: 43 / 100 Epoch 3 training complete Accuracy on evaluation data: 61 / 100 ... 

Itu lebih baik! Sehingga kita dapat melanjutkan lebih jauh, memutar setiap hiperparameter, dan secara bertahap meningkatkan efisiensi. Setelah mempelajari situasi dan menemukan nilai yang lebih baik untuk η, kami melanjutkan ke pencarian nilai yang baik untuk λ. Kemudian kita akan melakukan percobaan dengan arsitektur yang lebih kompleks, misalnya, dengan jaringan 10 neuron tersembunyi. Kemudian, kita kembali menyempurnakan parameter untuk η dan λ. Kemudian kita akan meningkatkan jaringan menjadi 20 neuron tersembunyi. Sedikit mengubah hyperparameter. Dan seterusnya, mengevaluasi efektivitas pada setiap langkah menggunakan bagian dari data pendukung kami, dan menggunakan perkiraan ini untuk memilih semua hyperparameter terbaik. Dalam proses peningkatan, dibutuhkan lebih banyak dan lebih banyak waktu untuk melihat efek penyetelan hyperparameter, sehingga kita dapat secara bertahap mengurangi frekuensi pelacakan.

Sebagai strategi keseluruhan, pendekatan ini terlihat menjanjikan. Namun, saya ingin kembali ke langkah pertama dalam mencari hyperparameters yang memungkinkan jaringan untuk belajar setidaknya. Bahkan, bahkan dalam contoh di atas, situasinya terlalu optimis. Bekerja dengan jaringan yang tidak belajar apa pun bisa sangat menjengkelkan. Anda dapat menyesuaikan hiperparameter selama beberapa hari, dan tidak menerima jawaban yang berarti. Karena itu, saya ingin menekankan sekali lagi bahwa pada tahap awal Anda perlu memastikan bahwa Anda bisa mendapatkan umpan balik cepat dari percobaan. Secara intuitif, sepertinya menyederhanakan masalah dan arsitektur hanya akan memperlambat Anda. Bahkan, ini mempercepat proses, karena Anda dapat menemukan jaringan dengan sinyal yang bermakna jauh lebih cepat. Setelah menerima sinyal seperti itu, Anda akan sering mendapatkan peningkatan cepat saat menyetel hyperparameter. Seperti dalam banyak situasi kehidupan, yang paling sulit adalah memulai proses.

Oke, ini adalah strategi umum. Sekarang mari kita lihat rekomendasi spesifik untuk meresepkan hyperparameter. Saya akan berkonsentrasi pada kecepatan belajar η, parameter regularisasi L2 λ, dan ukuran paket-mini. Namun, banyak komentar akan berlaku untuk hiperparameter lain, termasuk yang terkait dengan arsitektur jaringan, bentuk regularisasi lainnya, dan beberapa hiperparameter, yang akan kita pelajari di buku nanti, misalnya, koefisien momentum.

Kecepatan belajar

Misalkan kita meluncurkan tiga jaringan MNIST dengan tiga kecepatan belajar yang berbeda, η = 0,025, η = 0,25, dan η = 2,5, masing-masing. Kami akan meninggalkan sisa hyperparameters seperti pada bagian sebelumnya - 30 era, ukuran paket mini adalah 10, λ = 5.0. Kami juga akan kembali menggunakan semua 50.000 gambar pelatihan. Berikut ini adalah grafik yang menunjukkan perilaku biaya pelatihan (dibuat oleh program multiple_eta.py):



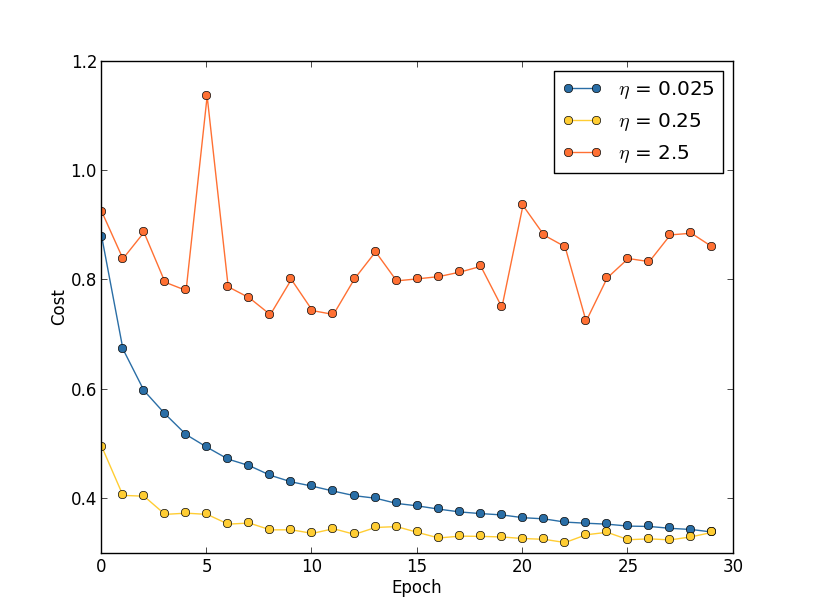
Pada η = 0,025, biaya berkurang dengan lancar ke era terakhir. Dengan η = 0,25, biaya awalnya menurun, tetapi setelah 20 zaman jenuh, sehingga sebagian besar perubahan berubah menjadi kecil dan, jelas, fluktuasi acak. Dengan η = 2.5, biaya sangat bervariasi sejak awal. Untuk memahami alasan fluktuasi ini, kita ingat bahwa penurunan gradien stokastik harus secara bertahap menurunkan kita ke lembah fungsi biaya:



Gambar ini membantu membayangkan secara intuitif apa yang terjadi, tetapi bukan penjelasan yang lengkap dan komprehensif. Lebih tepatnya, tetapi secara singkat, gradient descent menggunakan pendekatan orde pertama untuk fungsi biaya untuk memahami cara mengurangi biaya. Untuk η yang lebih besar, anggota dari fungsi biaya pesanan yang lebih tinggi menjadi lebih penting, dan mereka dapat mendominasi perilaku dengan memecah gradient descent. Ini sangat mungkin ketika mendekati minimum dan minimum lokal dari fungsi biaya, karena di samping titik-titik tersebut gradien menjadi kecil, yang membuatnya lebih mudah bagi anggota dari orde yang lebih tinggi untuk mendominasi.

Namun, jika η terlalu besar, maka langkah-langkahnya akan sangat besar sehingga mereka dapat melompat minimum, karena itu algoritma akan naik dari lembah. Mungkin inilah yang membuat harga terombang-ambing pada η = 2.5. Pilihan η = 0,25 mengarah pada fakta bahwa langkah-langkah awal benar-benar menuntun kita menuju fungsi biaya minimum, dan hanya ketika kita sampai di sana kita mulai mengalami kesulitan dengan melompat. Dan ketika kita memilih η = 0,025, kita tidak mengalami kesulitan seperti itu selama 30 zaman pertama. Tentu saja, pilihan nilai η yang demikian kecil menciptakan kesulitan lain - yaitu, memperlambat penurunan gradien stokastik. Pendekatan terbaik adalah memulai dengan η = 0.25, belajar 20 era, dan kemudian pergi ke η = 0.025. Nanti kita akan membahas tingkat pembelajaran variabel tersebut. Sementara itu, mari kita memikirkan pertanyaan menemukan satu nilai yang cocok untuk kecepatan belajar η.

Dengan mengingat hal ini, kita dapat memilih η sebagai berikut. Pertama, kami mengevaluasi nilai ambang η di mana biaya data pelatihan segera mulai berkurang, tetapi tidak berfluktuasi dan tidak meningkat. Estimasi ini tidak harus akurat. Urutan dapat diperkirakan dengan mulai dengan η = 0,01. Jika biaya berkurang di beberapa era pertama, maka ada baiknya mencoba η = 0,1, lalu 1,0, dan seterusnya, hingga Anda menemukan nilai di mana nilai berfluktuasi atau meningkat di era pertama. Dan sebaliknya, jika nilainya berfluktuasi atau meningkat pada zaman pertama dengan η = 0,01, maka coba η = 0,001, η = 0,0001, hingga Anda menemukan nilai penurunan biaya dalam beberapa zaman pertama. Prosedur ini akan memberi Anda urutan nilai ambang η. Jika mau, Anda dapat memperbaiki penilaian Anda dengan memilih nilai tertinggi untuk η, di mana biaya berkurang pada zaman pertama, misalnya, η = 0,5 atau η = 0,2 (ultra-presisi tidak diperlukan di sini). Ini memberi kita perkiraan nilai ambang η.

Nilai riil η, jelas, tidak boleh melebihi ambang yang dipilih. Bahkan, agar nilai η tetap berguna untuk banyak era, Anda sebaiknya menggunakan nilai dua kali lebih kecil dari ambang. Pilihan seperti itu biasanya memungkinkan Anda untuk belajar dari banyak era tanpa memperlambat belajar Anda.

Dalam kasus data MNIST, mengikuti strategi ini akan menghasilkan estimasi urutan ambang η pada 0,1. Setelah beberapa perbaikan, kami mendapatkan nilai η = 0,5. Dengan mengikuti resep di atas, kita harus menggunakan η = 0,25 untuk kecepatan belajar kita. Tetapi pada kenyataannya, saya menemukan bahwa η = 0,5 bekerja dengan baik untuk 30 era, jadi saya tidak khawatir tentang penurunannya.

Semua ini terlihat sangat mudah. Namun, menggunakan biaya pelatihan untuk memilih η tampaknya bertentangan dengan apa yang saya katakan sebelumnya - bahwa kami memilih hyperparameters, mengevaluasi efektivitas jaringan menggunakan data konfirmasi yang dipilih. Bahkan, kita akan menggunakan akurasi konfirmasi untuk memilih hiperparameter regularisasi, ukuran paket-mini dan parameter jaringan seperti jumlah lapisan dan neuron tersembunyi, dan sebagainya. Mengapa kita melakukan berbagai hal secara berbeda dengan kecepatan belajar? Jujur, pilihan ini adalah karena preferensi estetika pribadi saya, dan mungkin bias. Argumennya adalah bahwa hiperparameter lain harus meningkatkan akurasi klasifikasi akhir pada set tes, jadi masuk akal untuk memilih mereka berdasarkan keakuratan konfirmasi. Namun, tingkat pembelajaran hanya secara tidak langsung mempengaruhi akurasi klasifikasi akhir. Tujuan utamanya adalah untuk mengontrol ukuran langkah dari gradient descent, dan untuk melacak biaya pelatihan dengan cara terbaik untuk mengenali ukuran langkah yang terlalu besar. Tapi tetap ini preferensi estetika pribadi. Pada tahap awal pelatihan, biaya pelatihan biasanya berkurang hanya jika keakuratan konfirmasi meningkat, jadi dalam praktiknya tidak masalah kriteria mana yang digunakan.

Menggunakan pemberhentian awal untuk menentukan jumlah era pelatihan

Seperti yang kami sebutkan dalam bab ini, pemberhentian awal berarti bahwa pada akhir setiap era, kita perlu menghitung keakuratan klasifikasi pada data pendukung. Ketika berhenti membaik, kami berhenti bekerja. Akibatnya, pengaturan jumlah era menjadi urusan sederhana. Secara khusus, ini berarti bahwa kita tidak perlu secara khusus mengetahui bagaimana jumlah zaman tergantung pada hiperparameter lainnya. Ini terjadi secara otomatis. Selain itu, pemberhentian dini juga secara otomatis mencegah kita dari pelatihan ulang. Ini, tentu saja, itu baik, meskipun mungkin berguna untuk mematikan penghentian awal pada tahap awal percobaan sehingga Anda dapat melihat tanda-tanda pelatihan ulang dan menggunakannya untuk menyempurnakan pendekatan untuk regularisasi.

Untuk mengimplementasikan RO, kita perlu menjelaskan secara lebih spesifik apa yang dimaksud dengan “menghentikan peningkatan akurasi klasifikasi”. Seperti yang telah kita lihat, keakuratan dapat melompat sangat jauh ke sana kemari bahkan ketika tren secara keseluruhan membaik. Jika kita berhenti untuk pertama kalinya, ketika keakuratan menurun, maka kita hampir pasti tidak akan mencapai peningkatan lebih lanjut. Pendekatan terbaik adalah berhenti belajar jika akurasi klasifikasi terbaik tidak membaik untuk waktu yang lama. Misalkan, misalnya, kita terlibat dalam MNIST. Kemudian kita dapat memutuskan untuk menghentikan proses jika akurasi klasifikasi belum meningkat selama sepuluh era terakhir. Ini memastikan bahwa kami tidak berhenti terlalu dini karena kegagalan dalam pelatihan, tetapi kami tidak akan menunggu selamanya untuk setiap perbaikan yang tidak akan terjadi.

Aturan “no improvement over ten era” ini sangat cocok untuk studi MNIST awal. Namun, jaringan kadang-kadang dapat mencapai dataran tinggi di dekat akurasi klasifikasi tertentu, tinggal di sana selama beberapa waktu, dan kemudian mulai membaik lagi. Jika Anda perlu mencapai kinerja yang sangat baik, maka aturan "tidak ada peningkatan lebih dari sepuluh era" mungkin terlalu agresif untuk itu. Oleh karena itu, saya sarankan menggunakan aturan "tidak ada peningkatan lebih dari sepuluh era" untuk percobaan utama, dan secara bertahap mengadopsi aturan yang lebih lembut ketika Anda mulai lebih memahami perilaku jaringan Anda: "tidak ada peningkatan lebih dari dua puluh era", "tidak ada peningkatan lebih dari lima puluh era", dan seterusnya selanjutnya. Tentu saja, ini memberi kita hyperparameter lain untuk optimisasi! Namun dalam praktiknya, hyperparameter ini biasanya mudah disesuaikan untuk hasil yang baik. Dan untuk tugas-tugas selain MNIST, aturan "tidak ada peningkatan lebih dari sepuluh era" mungkin terlalu agresif, atau tidak cukup agresif, tergantung pada rincian tugas tertentu.Namun, setelah bereksperimen sedikit, biasanya cukup mudah untuk menemukan strategi pemberhentian awal yang cocok.

Kami belum menggunakan pemberhentian awal dalam percobaan kami dengan MNIST. Ini disebabkan oleh fakta bahwa kami membuat banyak perbandingan berbagai pendekatan untuk belajar. Untuk perbandingan seperti itu, berguna untuk menggunakan jumlah era yang sama dalam semua kasus. Namun, ada baiknya mengubah network2.py dengan memperkenalkan RO ke dalam program.

Tugasnya

• Ubah network2.py sehingga PO muncul di sana sesuai dengan aturan "no change for n epochs", di mana n adalah parameter yang dapat dikonfigurasi.
• Pikirkan aturan pemberhentian awal selain dari "tidak berubah dalam era". Idealnya, aturan tersebut harus mencari kompromi antara memperoleh akurasi dengan konfirmasi tinggi dan waktu pelatihan yang cukup singkat. Tambahkan aturan ke network2.py, dan jalankan tiga percobaan yang membandingkan akurasi validasi dan jumlah era pelatihan dengan aturan "tidak ada perubahan lebih dari 10 era".

Mempelajari Rencana Perubahan Kecepatan

Sementara kami menjaga kecepatan belajar η konstan. Namun, seringkali berguna untuk memodifikasinya. Pada tahap awal proses pelatihan, bobot kemungkinan besar dianggap salah sepenuhnya. Oleh karena itu, akan lebih baik menggunakan pelatihan kecepatan tinggi, yang akan menyebabkan bobot berubah lebih cepat. Kemudian Anda dapat mengurangi kecepatan pelatihan untuk membuat penyesuaian skala yang lebih baik.

Bagaimana kita menguraikan rencana untuk mengubah kecepatan belajar? Di sini Anda dapat menerapkan banyak pendekatan. Salah satu opsi alami adalah menggunakan ide dasar yang sama seperti di RO. Kami menjaga kecepatan pembelajaran konstan hingga keakuratan konfirmasi mulai memburuk. Kemudian kita mengurangi CO dengan jumlah tertentu, katakanlah, dua atau sepuluh kali. Kami mengulangi ini berkali-kali sampai CO 1024 (atau 1000) kali lebih sedikit dari yang awal. Dan selesaikan pelatihan.

Rencana untuk mengubah kecepatan belajar dapat meningkatkan efisiensi, dan juga membuka peluang besar untuk memilih rencana. Dan ini bisa menjadi sakit kepala - Anda dapat menghabiskan selamanya mengoptimalkan rencana. Untuk percobaan pertama, saya menyarankan menggunakan nilai CO konstan tunggal. Ini akan memberi Anda perkiraan pertama yang baik. Kemudian, jika Anda ingin memeras efisiensi terbaik dari jaringan, ada baiknya bereksperimen dengan rencana untuk mengubah kecepatan belajar seperti yang saya jelaskan. Sebuah karya ilmiah yang cukup mudah dibaca tahun 2010 menunjukkan keuntungan dari kecepatan belajar variabel saat menyerang MNIST.

Latihan

• Ubah network2.py sehingga mengimplementasikan rencana berikut untuk mengubah kecepatan belajar: membagi dua CR setiap kali keakuratan konfirmasi memenuhi aturan "no change in 10 epochs", dan berhenti belajar ketika kecepatan belajar turun ke 1/128 dari yang awal.

Parameter regularisasi λ

Saya sarankan memulai tanpa regularisasi sama sekali (λ = 0,0), dan menentukan nilai η, seperti yang ditunjukkan di atas. Dengan menggunakan nilai η yang dipilih, kita dapat menggunakan data pendukung untuk memilih nilai λ yang baik. Mulailah dengan λ = 1.0 (Saya tidak memiliki argumen yang bagus untuk memilih pilihan seperti itu), lalu naik atau turunkan sebanyak 10 kali untuk meningkatkan efisiensi dalam bekerja dengan mengonfirmasi data. Setelah menemukan urutan besarnya yang benar, kita dapat menyempurnakan nilai λ lebih tepat. Setelah ini, perlu untuk kembali ke optimasi η lagi.

Latihan

• , , λ η. , λ? , η?

Jika Anda menggunakan rekomendasi dari bagian ini, Anda akan melihat bahwa nilai yang dipilih dari η dan λ tidak selalu sama persis dengan yang saya gunakan sebelumnya. Hanya saja buku ini memiliki batasan teks, yang terkadang membuatnya tidak praktis untuk mengoptimalkan hyperparameter. Ingat semua perbandingan dari berbagai pendekatan pelatihan yang telah kami kerjakan - membandingkan fungsi biaya kuadratik dan entropi silang, metode lama dan baru untuk menginisialisasi bobot, dimulai dengan dan tanpa regularisasi, dan sebagainya. Untuk membuat perbandingan ini bermakna, saya mencoba untuk tidak mengubah hyperparameters antara pendekatan yang dibandingkan (atau skala mereka dengan benar). Tentu saja, tidak ada alasan untuk hiperparameter yang sama menjadi optimal untuk semua pendekatan pembelajaran yang berbeda, sehingga hiperparameter yang saya gunakan adalah hasil dari kompromi.

Sebagai alternatif, saya bisa mencoba untuk mengoptimalkan semua parameter hiper untuk setiap pendekatan untuk belajar secara maksimal. Ini akan menjadi pendekatan yang lebih baik dan lebih jujur, karena kami akan mengambil yang terbaik dari setiap pendekatan untuk belajar. Namun, kami membuat puluhan perbandingan, dan dalam praktiknya ini akan terlalu mahal secara komputasi. Oleh karena itu, saya memutuskan untuk berkompromi, untuk menggunakan opsi hyperparameter yang cukup baik (tetapi belum tentu optimal).

Ukuran Paket Mini

Bagaimana memilih ukuran paket mini? Untuk menjawab pertanyaan ini, pertama-tama mari kita asumsikan bahwa kita terlibat dalam pelatihan online, yaitu, kita menggunakan paket mini ukuran 1.

Masalah yang jelas dengan pembelajaran online adalah bahwa menggunakan paket mini yang terdiri dari satu contoh pelatihan akan menyebabkan kesalahan serius dalam memperkirakan gradien. Namun pada kenyataannya, kesalahan ini tidak akan menghadirkan masalah serius. Alasannya adalah bahwa estimasi gradien individu tidak harus sangat akurat. Kami hanya perlu mendapatkan perkiraan yang cukup akurat sehingga fungsi biaya kami berkurang. Seolah-olah Anda mencoba untuk sampai ke kutub magnet utara, tetapi Anda akan memiliki kompas yang tidak dapat diandalkan, dengan masing-masing pengukuran dikira 10-20 derajat. Jika Anda cukup sering memeriksa kompas, dan rata-rata akan menunjukkan arah yang benar, Anda pada akhirnya akan dapat mencapai kutub magnet utara.

Dengan argumen ini, tampaknya kita harus menggunakan pembelajaran online. Namun dalam kenyataannya situasinya agak lebih rumit. Dalam tugas ke bab terakhir, saya menunjukkan bahwa untuk menghitung pembaruan gradien untuk semua contoh dalam paket-mini, Anda dapat menggunakan teknik matriks pada saat yang sama, daripada loop. Bergantung pada perincian perangkat keras Anda dan pustaka aljabar linier, mungkin ternyata lebih cepat untuk menghitung taksiran paket mini, katakanlah, 100 daripada menghitung taksiran gradien untuk paket mini dalam siklus untuk 100 contoh pelatihan. Ini bisa berubah menjadi, misalnya, hanya 50 kali lebih lambat, dan bukan 100.

Pada awalnya tampaknya ini tidak banyak membantu kita. Dengan ukuran paket mini 100, aturan pelatihan untuk bobot terlihat seperti:

$$

$$w \rightarrow w' = w-\eta \frac{1}{100} \sum_x \nabla C_x \tag{100}$$

di mana penjumlahan membahas contoh pelatihan dalam paket mini. Bandingkan dengan

$$

$$w \rightarrow w' = w-\eta \nabla C_x \tag{101}$$

untuk pembelajaran online. Sekalipun dibutuhkan 50 kali lebih banyak waktu untuk memperbarui paket mini, pelatihan online tampaknya masih menjadi pilihan terbaik, karena kita akan lebih sering diperbarui. Namun, misalkan dalam kasus paket mini, kami meningkatkan kecepatan belajar 100 kali, maka aturan pembaruan berubah menjadi:

$$

$$w \rightarrow w' = w-\eta \sum_x \nabla C_x \tag{102}$$

Ini mirip dengan 100 tahapan pembelajaran online yang terpisah dengan kecepatan belajar η. Namun, satu langkah dalam pembelajaran online hanya membutuhkan waktu 50 kali lipat. Tentu saja, pada kenyataannya ini bukan 100 level pembelajaran online, karena dalam paket-mini semua ∇C _x dievaluasi untuk set bobot yang sama, berbeda dengan pembelajaran kumulatif yang terjadi pada case online. Namun tampaknya menggunakan paket mini yang lebih besar akan mempercepat prosesnya.

Mengingat semua faktor ini, memilih ukuran mini-pack terbaik adalah kompromi. Pilih terlalu kecil dan tidak mendapatkan manfaat penuh dari perpustakaan matriks yang baik yang dioptimalkan untuk perangkat keras cepat. Pilih yang terlalu besar, dan tidak akan cukup sering memperbarui bobot. Anda perlu memilih nilai kompromi yang memaksimalkan kecepatan belajar. Untungnya, pilihan ukuran paket mini di mana kecepatan dimaksimalkan relatif independen dari hyperparameters lainnya (kecuali untuk arsitektur umum), oleh karena itu, untuk menemukan ukuran paket mini yang baik, tidak perlu untuk mengoptimalkannya. Oleh karena itu, akan cukup untuk menggunakan nilai yang dapat diterima (belum tentu optimal) untuk hiperparameter lainnya, dan kemudian mencoba beberapa ukuran paket mini yang berbeda, penskalaan η, seperti ditunjukkan di atas.Bangun grafik akurasi konfirmasi versus waktu (waktu berlalu sebenarnya, bukan era!), Dan pilih ukuran paket mini yang memberikan peningkatan kinerja tercepat. Dengan ukuran paket mini yang dipilih, Anda dapat melanjutkan untuk mengoptimalkan hyperparameter lainnya.

Tentu saja, karena Anda sudah pasti mengerti, dalam pekerjaan kami, saya tidak melakukan optimasi seperti itu. Dalam implementasi Majelis Nasional kami, pendekatan cepat untuk memperbarui paket mini tidak digunakan sama sekali. Saya hanya menggunakan paket mini ukuran 10 tanpa berkomentar atau menjelaskannya, di hampir semua contoh. Secara umum, kami dapat mempercepat pembelajaran dengan mengurangi ukuran paket-mini. Saya tidak melakukan ini, khususnya, karena percobaan awal saya menunjukkan bahwa akselerasi akan agak sederhana. Tetapi dalam implementasi praktis, kami pasti ingin menerapkan pendekatan tercepat untuk memperbarui paket mini, dan mencoba untuk mengoptimalkan ukurannya untuk memaksimalkan kecepatan keseluruhan.

Teknik Otomatis

Saya menggambarkan pendekatan heuristik ini sebagai sesuatu yang perlu diubah dengan tangan. Optimalisasi manual adalah cara yang baik untuk mendapatkan ide tentang cara kerja NS. Namun, dan, kebetulan, tidak mengherankan bahwa banyak pekerjaan telah dilakukan pada otomatisasi proyek ini. Teknik umum adalah pencarian kisi yang secara sistematis menyaring kisi dalam ruang hyperparameter. Tinjauan tentang pencapaian dan keterbatasan teknik ini (serta rekomendasi tentang alternatif yang mudah diimplementasikan) dapat ditemukan di 2012 . Banyak teknik canggih telah diusulkan. Saya tidak akan meninjau semuanya, tapi saya ingin mencatat karya yang menjanjikan tahun 2012, menggunakan optimasi Bayesian dari hiperparameter. Kode dari kantor terbuka untuk semua orang , dan dengan beberapa keberhasilan digunakan oleh peneliti lain.

Ringkaslah

Menggunakan aturan praktik yang telah saya jelaskan, Anda tidak akan mendapatkan hasil terbaik dari PS Anda dari semua kemungkinan. Tetapi mereka cenderung memberi Anda titik awal dan dasar yang baik untuk perbaikan lebih lanjut. Secara khusus, saya pada dasarnya menggambarkan hiperparameter secara independen. Dalam praktiknya, ada hubungan di antara mereka. Anda dapat bereksperimen dengan η, memutuskan bahwa Anda telah menemukan nilai yang benar, kemudian mulai mengoptimalkan λ, dan menemukan bahwa itu melanggar optimasi η Anda. Dalam praktiknya, berguna untuk bergerak ke arah yang berbeda, secara bertahap mendekati nilai-nilai yang baik. Yang terpenting, ingatlah bahwa pendekatan heuristik yang saya jelaskan adalah aturan praktik sederhana, tetapi bukan sesuatu yang diukir di atas batu. Anda perlu mencari tanda-tanda bahwa ada sesuatu yang tidak berfungsi dan memiliki keinginan untuk bereksperimen. Khususnyahati-hati memonitor perilaku jaringan saraf Anda, terutama keakuratan konfirmasi.

Kompleksitas pilihan hiperparameter diperparah oleh fakta bahwa pengetahuan praktis pilihan mereka tersebar di banyak penelitian dan program penelitian, dan seringkali hanya di kepala praktisi individu. Ada sejumlah besar pekerjaan dengan deskripsi tentang apa yang harus dilakukan (seringkali saling bertentangan). Namun, ada beberapa karya yang sangat berguna yang mensintesis dan menyoroti sebagian besar pengetahuan ini. Di dalam Yosua Benji dari 2012 memberikan saran praktis tentang penggunaan back-propagasi gradien keturunan dan pelatihan bagi Majelis Nasional, termasuk Majelis Nasional dan mendalam. Benjio menjelaskan banyak detail dengan lebih detail. Dari saya, termasuk pencarian sistematis untuk hiperparameter. Pekerjaan bagus lainnya adalah bekerja.1998 Yanna Lekuna dan yang lainnya. Kedua karya ini muncul dalam buku yang sangat berguna tahun 2012, yang berisi banyak trik yang sering digunakan dalam Majelis Nasional: " Jaringan saraf: trik kerajinan ." Buku itu mahal, tetapi banyak artikelnya diposting di Internet oleh penulisnya, dan mereka dapat ditemukan di mesin pencari.

Dari artikel-artikel ini, dan terutama dari percobaan kami sendiri, satu hal menjadi jelas: masalah mengoptimalkan hiperparameter tidak bisa disebut sepenuhnya diselesaikan. Selalu ada trik lain yang bisa Anda coba untuk meningkatkan efisiensi. Penulis memiliki pepatah bahwa sebuah buku tidak dapat diselesaikan, tetapi hanya dapat dijatuhkan. Hal yang sama berlaku untuk optimasi NS: ruang hyperparameters sangat besar sehingga optimasi tidak dapat diselesaikan, tetapi hanya dapat dihentikan, meninggalkan NS ke turunan. Jadi tujuan Anda adalah untuk mengembangkan alur kerja yang memungkinkan Anda untuk dengan cepat melakukan pengoptimalan yang baik, sambil memberi Anda kesempatan untuk mencoba opsi pengoptimalan yang lebih terperinci jika perlu.

Kesulitan dengan pemilihan hiperparameter membuat beberapa orang mengeluh bahwa NSs membutuhkan terlalu banyak usaha dibandingkan dengan teknik MO lainnya. Saya telah mendengar banyak varian keluhan seperti: “Ya, NS yang disesuaikan dengan baik dapat memberikan efisiensi terbaik saat memecahkan masalah. Tetapi di sisi lain, saya dapat mencoba hutan acak [atau SVM, atau teknologi favorit Anda lainnya], dan hanya berfungsi. Saya tidak punya waktu untuk mencari tahu NA mana yang tepat untuk saya. " Tentu saja, dari sudut pandang praktis, ada baiknya memiliki teknik yang mudah digunakan di bawah seorang teman. Ini sangat baik ketika Anda baru mulai bekerja dengan tugas, dan masih belum jelas apakah MO dapat membantu menyelesaikannya sama sekali. Di sisi lain, jika penting bagi Anda untuk mencapai hasil yang optimal, Anda mungkin perlu mencoba beberapa pendekatan yang membutuhkan pengetahuan khusus. Itu akan bagusjika MO selalu mudah, tetapi tidak ada alasan mengapa itu harus menjadi sepele priori.

Teknik lainnya

Masing-masing teknik yang dikembangkan dalam bab ini sangat berharga, tetapi ini bukan satu-satunya alasan saya menggambarkannya. Lebih penting untuk membiasakan diri dengan beberapa masalah yang mungkin muncul di bidang NA, dan dengan gaya analisis yang dapat membantu mengatasinya. Di satu sisi, kita belajar bagaimana berpikir tentang NS. Di sisa bab ini, saya akan menjelaskan secara singkat seperangkat teknik lain. Deskripsi mereka tidak akan sedalam yang sebelumnya, tetapi mereka harus menyampaikan beberapa sensasi mengenai berbagai teknik yang ditemukan di bidang NA.

Variasi keturunan gradien stokastik

Penurunan gradien stokastik melalui backpropagation membantu kami dengan baik selama serangan terhadap masalah mengklasifikasikan angka tulisan tangan dari MNIST. Namun, ada banyak pendekatan lain untuk mengoptimalkan fungsi biaya, dan kadang-kadang mereka menunjukkan efisiensi yang lebih baik daripada penurunan gradien stokastik dengan paket mini. Di bagian ini, saya jelaskan secara singkat dua pendekatan seperti itu, Goni dan momentum.

Goni

Untuk memulai, mari kita kesampingkan Majelis Nasional. Sebaliknya, kami hanya mempertimbangkan masalah abstrak meminimalkan fungsi biaya C dari banyak variabel, w = w1, w2, ..., yaitu, C = C (w). Dengan teorema Taylor, fungsi biaya pada titik w dapat diperkirakan:

$$

$$C(w+\Delta w) = C(w) + \sum_j \frac{\partial C}{\partial w_j} \Delta w_j \nonumber \\ + \frac{1}{2} \sum_{jk} \Delta w_j \frac{\partial^2 C}{\partial w_j \partial w_k} \Delta w_k + \ldots \tag{103}$$

Kita dapat menulis ulang dengan lebih ringkas sebagai

$$

$$C(w+\Delta w) = C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w + \ldots \tag{104}$$

di mana ∇C adalah vektor gradien biasa, dan H adalah matriks yang dikenal sebagai matriks Hessian , di mana jk berisi ∂ ² C / ∂w _j ∂w _k . Misalkan kita memperkirakan C dengan meninggalkan istilah tingkat tinggi yang bersembunyi di balik elipsis dalam rumus:

$$

$$C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w \tag{105}$$

Dengan menggunakan aljabar, dapat ditunjukkan bahwa ekspresi di sisi kanan dapat diminimalkan dengan memilih:

$$

$$\Delta w = -H^{-1} \nabla C \tag{106}$$

Tegasnya, agar ini menjadi minimum, dan bukan hanya ekstrem, kita harus mengasumsikan bahwa matriks Hessian lebih pasti positif. Secara intuitif, ini berarti bahwa fungsi C seperti lembah, bukan gunung atau pelana.

Jika (105) merupakan perkiraan yang baik untuk fungsi biaya, diharapkan transisi dari titik w ke titik w + Δw = w - H - 1 −C harus secara signifikan mengurangi fungsi biaya. Ini menawarkan kemungkinan algoritma minimisasi biaya:

• Pilih titik awal w.
• Perbarui w ke titik baru, w ′ = w - H ⁻¹ ∇C, di mana H G dan H ∇C dihitung dalam w.
• w' , w′′=w′−H′ ⁻¹ ∇′C, H ∇C w'.
• ...

Dalam praktiknya, (105) hanya perkiraan, dan lebih baik mengambil langkah yang lebih kecil. Kami akan melakukan ini dengan terus memperbarui w oleh Δw = −ηH - 1∇C, di mana η adalah kecepatan belajar.

Pendekatan ini untuk meminimalkan fungsi biaya dikenal sebagai optimasi Hessian. Ada hasil teoritis dan empiris yang menunjukkan bahwa metode Hessian konvergen ke minimum dalam langkah yang lebih sedikit daripada penurunan gradien standar. Secara khusus, dengan memasukkan informasi tentang perubahan urutan kedua dalam fungsi biaya, dimungkinkan untuk menghindari banyak patologi yang ditemukan pada gradient descent dalam pendekatan Hessian. Selain itu, ada versi algoritma backpropagation yang dapat digunakan untuk menghitung Hessian.

Jika optimasi Hessian sangat keren, lalu mengapa kita tidak menggunakannya di NS kami? Sayangnya, meskipun memiliki banyak sifat yang diinginkan, ada satu yang sangat tidak diinginkan: sangat sulit untuk dipraktikkan. Bagian dari masalahnya adalah ukuran besar dari matriks Hessian. Misalkan kita memiliki NS dengan 10 ⁷ bobot dan offset. Kemudian dalam matriks Goni yang sesuai akan ada 10 ⁷ × 10 ⁷ = 10 ¹⁴ elemen. Terlalu banyak! Akibatnya , ternyata sangat sulit untuk menghitung H ⁻¹ ∇C dalam praktiknya. Tetapi ini tidak berarti bahwa tidak ada gunanya mengetahui tentang dia. Banyak pilihan gradient descent terinspirasi oleh optimisasi Hessian, mereka hanya menghindari masalah matriks yang terlalu besar. Mari kita lihat satu teknik seperti itu, penurunan gradien impuls.

Penurunan gradien berdasarkan impuls

Secara intuitif, keuntungan dari optimasi Hessian adalah bahwa ia tidak hanya mencakup informasi tentang gradien, tetapi juga informasi tentang perubahannya. Penurunan gradien berbasis impuls didasarkan pada intuisi yang sama, tetapi menghindari matriks besar dari turunan kedua. Untuk memahami teknik impuls, mari kita ingat gambar gradient descent pertama kami, di mana kami memeriksa bola yang bergulir di lembah. Lalu kami melihat bahwa gradient descent, yang bertentangan dengan namanya, hanya sedikit menyerupai bola yang jatuh ke bawah. Teknik pulsa mengubah gradient descent di dua tempat, yang membuatnya lebih seperti gambar fisik. Pertama, ia memperkenalkan konsep "kecepatan" untuk parameter yang kami coba optimalkan. Gradien mencoba mengubah kecepatan, bukan "lokasi" secara langsung, mirip dengan bagaimana kekuatan fisik mengubah kecepatan,dan hanya secara tidak langsung mempengaruhi lokasi. Kedua, metode impuls adalah semacam istilah gesekan yang secara bertahap mengurangi kecepatan.

Mari kita berikan definisi yang lebih tepat secara matematis. Kami memperkenalkan variabel kecepatan v = v1, v2, ..., satu untuk setiap variabel yang sesuai dengan _wj (dalam jaringan saraf, variabel-variabel ini secara alami mencakup semua bobot dan perpindahan). Kemudian kita mengubah aturan pembaruan gradient descent w → w ′ = w - η∇C menjadi

$$

$$v \rightarrow v' = \mu v - \eta \nabla C \tag{107}$$

$$

$$w \rightarrow w' = w+v' \tag{108}$$

Dalam persamaan, μ adalah hiperparameter yang mengontrol jumlah pengereman atau gesekan sistem. Untuk memahami arti persamaan, pertama-tama berguna untuk mempertimbangkan kasus di mana μ = 1, yaitu, ketika tidak ada gesekan. Dalam kasus ini, studi persamaan menunjukkan bahwa sekarang "gaya" ∇C mengubah kecepatan v, dan kecepatan mengontrol laju perubahan w. Secara intuitif, kecepatan dapat diperoleh dengan terus-menerus menambahkan anggota gradien ke dalamnya. Ini berarti bahwa jika gradien bergerak di sekitar satu arah selama beberapa tahap pelatihan, kita dapat memperoleh kecepatan gerakan yang cukup tinggi di arah ini. Bayangkan, misalnya, apa yang terjadi ketika bergerak menuruni bukit:



Dengan setiap langkah menuruni lereng, kecepatan meningkat, dan kami bergerak lebih cepat dan lebih cepat ke dasar lembah. Ini memungkinkan teknik kecepatan berjalan lebih cepat daripada penurunan gradien standar. Tentu saja, masalahnya adalah, setelah mencapai dasar lembah, kita akan melewatinya. Atau, jika gradien berubah terlalu cepat, mungkin kita bergerak ke arah yang berlawanan. Ini adalah titik memperkenalkan hyperparameter μ in (107). Saya katakan sebelumnya bahwa μ mengontrol jumlah gesekan dalam sistem; lebih tepatnya, jumlah gesekan harus dibayangkan sebagai 1-μ. Ketika μ = 1, seperti yang kita lihat, tidak ada gesekan, dan kecepatan sepenuhnya ditentukan oleh gradien ∇C. Dan sebaliknya, ketika μ = 0, ada banyak gesekan, tidak ada kecepatan yang diperoleh, dan persamaan (107) dan (108) direduksi menjadi persamaan gradient descent yang biasa, w → w ′ = w - η∇C. Dalam praktek,menggunakan nilai μ dalam interval antara 0 dan 1 dapat memberi kita keuntungan dari kemampuan untuk mendapatkan kecepatan tanpa bahaya tergelincir minimum. Kita dapat memilih nilai untuk μ menggunakan data konfirmasi yang tertunda dalam banyak cara yang sama seperti kita memilih nilai untuk η dan λ.

Sejauh ini saya telah menghindari penamaan hyperparameter μ. Faktanya adalah bahwa nama standar untuk μ dipilih dengan buruk: itu disebut koefisien momentum. Ini bisa membingungkan karena μ sama sekali tidak menyukai konsep momentum dari fisika. Ini jauh lebih kuat terkait dengan gesekan. Namun, istilah "koefisien momentum" banyak digunakan, jadi kami akan terus menggunakannya juga.

Fitur bagus dari teknik impuls adalah bahwa hampir tidak ada yang perlu dilakukan untuk mengubah implementasi gradient descent untuk memasukkan teknik ini di dalamnya. Kita masih dapat menggunakan propagasi balik untuk menghitung gradien, seperti sebelumnya, dan menggunakan ide-ide seperti memeriksa minipack yang dipilih secara stokastik. Dalam hal ini, kita bisa mendapatkan beberapa manfaat dari optimasi Hessian menggunakan informasi tentang perubahan gradien. Namun, semua ini terjadi tanpa cacat, dan hanya dengan perubahan kode kecil. Dalam praktiknya, teknik impuls banyak digunakan dan sering membantu mempercepat pembelajaran.

Latihan

• Apa yang salah jika kita menggunakan μ> 1 dalam teknik pulsa?
• Apa yang salah jika kita menggunakan μ <0 dalam teknik pulsa?

Tantangan

• Tambahkan penurunan gradien stokastik berbasis momentum ke network2.py.

Pendekatan lain untuk meminimalkan fungsi biaya

Banyak pendekatan lain telah dikembangkan untuk meminimalkan fungsi biaya, dan tidak ada kesepakatan telah dicapai pada pendekatan terbaik. Menuju lebih dalam ke topik jaringan saraf, penting untuk mempelajari teknologi lain, memahami cara kerjanya, apa kekuatan dan kelemahannya, dan bagaimana mempraktikkannya. Dalam karya yang saya sebutkan sebelumnya , beberapa teknik tersebut diperkenalkan dan dibandingkan, termasuk gradient descent berpasangan dan metode BFGS (dan juga mempelajari metode BFGS terkait erat dengan batas memori, atau L-BFGS ). Teknologi lain yang baru-baru ini menunjukkan hasil yang menjanjikan., ini adalah gradien percepatan Nesterov, meningkatkan teknik denyut nadi. Namun, penurunan gradien sederhana bekerja dengan baik untuk banyak tugas, terutama saat menggunakan momentum, jadi kami akan tetap menggunakan penurunan gradien stokastik sampai akhir buku ini.

Model lain dari neuron buatan

Sejauh ini, kami telah membuat NS kami menggunakan neuron sigmoid. Pada prinsipnya, NS yang dibangun di atas neuron sigmoid dapat menghitung fungsi apa pun. Namun dalam praktiknya, jaringan yang dibangun di atas model neuron lain kadang-kadang di atas yang sigmoid. Bergantung pada aplikasinya, jaringan yang didasarkan pada model alternatif semacam itu dapat belajar lebih cepat, lebih baik menggeneralisasikan data verifikasi, atau melakukan keduanya. Izinkan saya menyebutkan beberapa model neuron alternatif untuk memberi Anda gambaran tentang beberapa opsi yang umum digunakan.

Mungkin variasi paling sederhana adalah tang neuron menggantikan fungsi sigmoid dengan tangen hiperbolik. Output dari neuron tang dengan input x, vektor bobot w, dan offset b ditetapkan sebagai

$$

$$\tanh(w \cdot x+b) \tag{109}$$

di mana tanh secara alami tangen hiperbolik . Ternyata dia sangat erat terhubung dengan neuron sigmoid. Untuk melihat ini, ingat bahwa tanh didefinisikan sebagai

$$

$$\tanh(z) \equiv \frac{e^z-e^{-z}}{e^z+e^{-z}} \tag{110}$$

Menggunakan aljabar kecil, mudah untuk melihatnya

$$

$$\sigma(z) = \frac{1+\tanh(z/2)}{2} \tag{111}$$

yaitu, tanh hanya meningkatkan sigmoid. Secara grafis, Anda juga dapat melihat bahwa fungsi tanh memiliki bentuk yang sama dengan sigmoid: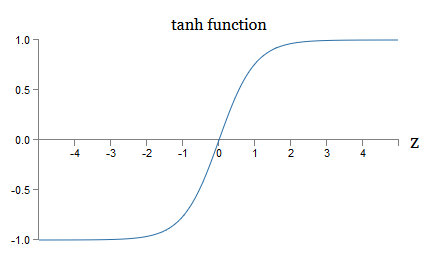



Satu perbedaan antara neuron tang dan neuron sigmoid adalah bahwa output dari pertama meluas dari -1 ke 1, dan bukan dari 0 ke 1. Ini berarti bahwa ketika membuat jaringan berdasarkan tang neuron, Anda mungkin perlu menormalkan output Anda (dan, tergantung pada detail aplikasi, mungkin input) sedikit berbeda dari pada jaringan sigmoid.

Seperti yang sigmoid, tang neuron, pada prinsipnya, dapat menghitung fungsi apa pun (walaupun ada beberapa trik), menandai input dari -1 hingga 1. Selain itu, gagasan propagasi balik dan penurunan gradien stokastik sama mudahnya diterapkan pada tang -Euron, serta sigmoid.

Latihan

• Buktikan persamaan (111).

Jenis neuron apa yang harus digunakan dalam jaringan, tang atau sigmoid? Jawabannya, sejujurnya, tidak jelas! Namun, ada argumen teoretis dan beberapa bukti empiris bahwa tang neuron terkadang bekerja lebih baik. Mari kita secara singkat membahas salah satu argumen teoretis yang mendukung tang neuron. Misalkan kita menggunakan neuron sigmoid, dan semua aktivasi pada jaringan akan positif. Pertimbangkan bobot w ^{l + 1} _jk termasuk untuk neuron No. j di lapisan No. l + 1. Aturan backpropagation (BP4) memberi tahu kita bahwa gradien yang terkait dengan ini akan sama dengan ^l _k δ ^{l + 1} _j . Karena aktivasi positif, tanda gradien ini akan sama dengan tanda δ ^{l + 1} _j. Ini berarti bahwa jika δ ^{l + 1} _j positif, maka semua bobot w ^{l + 1} _jk akan berkurang selama gradient descent, dan jika δ ^{l + 1} _j negatif, maka semua bobot w ^{l + 1} _jkakan meningkat selama gradient descent. Dengan kata lain, semua bobot yang terkait dengan neuron yang sama akan naik atau turun bersama. Dan ini merupakan masalah, karena Anda mungkin perlu menambah bobot sambil mengurangi yang lain. Tetapi ini hanya dapat terjadi jika beberapa aktivasi input memiliki tanda yang berbeda. Ini menunjukkan perlunya mengganti sigmoid dengan fungsi aktivasi lain, misalnya, tangen hiperbolik, yang memungkinkan aktivasi menjadi positif dan negatif. Memang, karena tanh simetris terhadap nol, tanh (−z) = −tanh (z), orang dapat berharap bahwa, secara kasar, aktivasi dalam lapisan tersembunyi akan terdistribusi secara merata antara positif dan negatif. Ini akan membantu memastikan bahwa tidak ada bias sistematis dalam pembaruan skala dalam satu arah atau lainnya.

Seberapa serius argumen ini dipertimbangkan? Bagaimanapun, ini heuristik, tidak memberikan bukti ketat bahwa tang neuron lebih unggul daripada yang sigmoid. Mungkin neuron sigmoid memiliki beberapa sifat yang mengkompensasi masalah ini? Memang, dalam banyak kasus, fungsi tanh menunjukkan dari minimal hingga tidak ada keuntungan dibandingkan dengan sigmoid. Sayangnya, kami tidak memiliki metode yang sederhana dan cepat diimplementasikan untuk memeriksa jenis neuron mana yang akan belajar lebih cepat atau akan terbukti lebih efektif dalam generalisasi untuk kasus tertentu.

Varian lain dari neuron sigmoid adalah neuron linear terkoreksi, atau unit linear terkoreksi, ReLU. Output ReLU dengan input x, vektor bobot w dan offset b ditentukan sebagai berikut:

$$

$$\max(0, w \cdot x+b) \tag{112}$$

Fungsi meluruskan grafik maks (0, z) terlihat seperti ini:



Neuron semacam itu, jelas, sangat berbeda dari neuron sigmoid dan tang. Namun, mereka serupa karena mereka juga dapat digunakan untuk menghitung fungsi apa pun, dan mereka dapat dilatih menggunakan propagasi balik dan penurunan gradien stokastik.

Kapan saya harus menggunakan ReLU alih-alih neuron sigmoid atau tang? Dalam karya terbaru tentang pengenalan gambar ( 1 , 2 , 3 , 4) Keuntungan serius menggunakan ReLU ditemukan di hampir seluruh jaringan. Namun, seperti halnya dengan neuron tang, kita belum memiliki pemahaman yang benar-benar mendalam tentang kapan tepatnya ReLU mana yang lebih disukai, dan mengapa. Untuk mengetahui beberapa masalah, ingat bahwa neuron sigmoid berhenti belajar ketika jenuh, yaitu ketika output mendekati 0 atau 1. Seperti yang telah kita lihat berulang kali dalam bab ini, masalahnya adalah bahwa anggota σ mengurangi gradien yang memperlambat belajar. Neuron Tang menderita kesulitan yang sama dalam saturasi. Pada saat yang sama, peningkatan input tertimbang pada ReLU tidak akan pernah membuatnya jenuh, oleh karena itu, perlambatan yang sesuai dalam pelatihan tidak akan terjadi. Di sisi lain, ketika input tertimbang pada ReLU negatif, gradien menghilang dan neuron berhenti belajar sama sekali.Ini hanya beberapa dari banyak masalah yang membuatnya tidak sepele untuk memahami kapan dan bagaimana ReLU berperilaku lebih baik daripada neuron sigmoid atau tang.

Saya melukis gambar ketidakpastian, menekankan bahwa kami belum memiliki teori yang kuat tentang pilihan fungsi aktivasi. Memang, masalah ini bahkan lebih rumit daripada yang saya jelaskan, karena ada banyak kemungkinan fungsi aktivasi. Yang mana yang akan memberi kita jaringan pembelajaran tercepat? Yang akan memberikan akurasi terbesar dalam tes? Saya terkejut betapa sedikit studi yang sangat mendalam dan sistematis tentang masalah ini. Idealnya, kita harus memiliki teori yang memberi tahu kita secara terperinci bagaimana memilih (dan mungkin berubah dengan cepat) fungsi aktivasi kita. Di sisi lain, kita tidak boleh dihentikan oleh kurangnya teori yang lengkap! Kami sudah memiliki alat yang kuat, dan dengan bantuan mereka kami dapat mencapai kemajuan yang signifikan. Sampai akhir buku ini saya akan menggunakan neuron sigmoid sebagai yang utama,karena mereka bekerja dengan baik dan memberikan ilustrasi konkret tentang ide-ide kunci yang terkait dengan Majelis Nasional. Tetapi perlu diingat bahwa ide yang sama dapat diterapkan pada neuron lain, dan opsi ini memiliki kelebihan.

: , , ? ?

: , . , . . : , , ?

—

Suatu kali di sebuah konferensi tentang dasar-dasar mekanika kuantum, saya memperhatikan sesuatu yang tampak seperti kebiasaan berbicara yang lucu: di akhir laporan, pertanyaan para penonton sering dimulai dengan frasa: "Saya sangat menyukai sudut pandang Anda, tapi ..." Dasar-dasar kuantum bukan bidang yang biasa saya, dan saya menarik perhatian pada gaya mengajukan pertanyaan ini karena pada konferensi ilmiah lainnya saya praktis tidak bertemu dengan penanya yang menunjukkan simpati terhadap sudut pandang pembicara. Pada saat itu, saya memutuskan bahwa prevalensi pertanyaan seperti itu menunjukkan bahwa kemajuan fundamental kuantum dicapai cukup sedikit, dan bahwa orang-orang baru mulai mendapatkan momentum. Kemudian saya menyadari bahwa penilaian ini terlalu keras. Para pembicara bergumul dengan beberapa masalah paling sulit yang pernah ada dalam benak manusia. Secara alami, kemajuan berjalan lambat!Namun, masih ada nilai dalam mendengar berita tentang pemikiran orang tentang daerah ini, bahkan jika mereka tidak memiliki apa-apa.

Dalam buku ini Anda mungkin telah memperhatikan "detak saraf" yang mirip dengan frasa "Saya sangat terkesan." Untuk menjelaskan apa yang kita miliki, saya sering menggunakan kata-kata seperti "heuristik" atau "berbicara kasar", diikuti dengan penjelasan tentang fenomena tertentu. Kisah-kisah ini dapat dipercaya, tetapi bukti empiris seringkali cukup dangkal. Jika Anda mempelajari literatur penelitian, Anda akan melihat bahwa cerita-cerita semacam ini muncul di banyak makalah penelitian tentang jaringan saraf, sering di perusahaan sejumlah kecil bukti yang mendukung mereka. Bagaimana kita berhubungan dengan cerita seperti itu?

Dalam banyak bidang ilmu pengetahuan - terutama di mana fenomena sederhana dipertimbangkan - orang dapat menemukan bukti yang sangat ketat dan dapat diandalkan dari hipotesis yang sangat umum. Tetapi di Majelis Nasional ada sejumlah besar parameter dan hiperparameter, dan ada hubungan yang sangat kompleks di antara mereka. Dalam sistem yang sangat kompleks ini, sangat sulit untuk membuat pernyataan umum yang andal. Pemahaman NS dalam semua kepenuhannya, seperti yayasan kuantum, menguji batas-batas pikiran manusia. Seringkali kita harus membuang bukti yang mendukung atau menentang beberapa kasus khusus dari pernyataan umum. Akibatnya, pernyataan-pernyataan ini kadang-kadang diminta untuk diubah atau ditinggalkan, ketika bukti baru muncul.

Salah satu pendekatan untuk situasi ini adalah untuk mempertimbangkan bahwa setiap cerita heuristik tentang NS menyiratkan tantangan tertentu. Sebagai contoh, perhatikan penjelasan yang saya kutip tentang mengapa pengecualian (putus sekolah) dari pekerjaan di 2012 bekerja.: “Teknik ini mengurangi adaptasi sendi yang kompleks dari neuron, karena neuron tidak dapat bergantung pada kehadiran tetangga tertentu. Pada akhirnya, ia harus mempelajari sifat-sifat yang lebih andal yang dapat berguna dalam bekerja bersama dengan banyak subset neuron acak yang berbeda. ” Pernyataan yang kaya dan provokatif, atas dasar di mana Anda dapat membangun seluruh program penelitian, di mana Anda perlu mencari tahu apa yang benar, di mana itu salah, dan apa yang perlu diklarifikasi dan diubah. Dan sekarang benar-benar ada seluruh industri peneliti yang mempelajari pengecualian (dan banyak variasinya), mencoba memahami cara kerjanya dan keterbatasan apa yang dimilikinya. Demikian juga dengan banyak pendekatan heuristik lain yang kami diskusikan. Masing-masing tidak hanya penjelasan potensial,tetapi juga tantangan untuk penelitian dan pemahaman yang lebih rinci.

Tentu saja, tidak seorang pun akan memiliki cukup waktu untuk menyelidiki semua penjelasan heuristik ini dengan cukup dalam. Seluruh komunitas peneliti NS akan membutuhkan waktu puluhan tahun untuk mengembangkan teori pelatihan NS yang sangat kuat berdasarkan bukti. Apakah ini berarti bahwa ada baiknya menolak penjelasan heuristik sebagai lemah dan kurang bukti? Tidak! Kita membutuhkan heuristik yang akan menginspirasi pemikiran kita. Ini mirip dengan era penemuan geografis yang hebat: para sarjana awal sering bertindak (dan membuat penemuan) berdasarkan kepercayaan yang salah secara serius. Kemudian, kami memperbaiki kesalahan ini, mengisi kembali pengetahuan geografis kami. Ketika Anda memahami sesuatu dengan buruk - seperti para peneliti memahami geografi, dan seperti yang kita pahami NS saat ini - lebih penting untuk dengan berani mempelajari yang tidak diketahui,daripada benar benar pada setiap langkah penalaran Anda. Oleh karena itu, Anda harus mempertimbangkan kisah-kisah ini sebagai instruksi yang berguna tentang cara merenungkan NS, menjaga kesadaran yang sehat akan keterbatasannya, dan dengan hati-hati memantau keandalan bukti dalam setiap kasus. Dengan kata lain, kita membutuhkan cerita yang bagus untuk motivasi dan inspirasi, dan investigasi menyeluruh yang teliti untuk menemukan fakta nyata.