Fisika dan Ekonomi. Perbedaan gnoseologis dan manifestasinya dalam IT

Saya datang ke dunia IT dari fisika teoretis. Dia terutama terlibat dalam tugas ekonomi. Terlibat - ini: analisis, TK, pernyataan, desain, pemrograman. Secara alami, setiap saat saya membandingkan pendekatan fisik dan ekonomi untuk memahami hukum alam dan ekonomi. Suatu sudut pandang tertentu telah matang tentang hal ini. Tentang dia dan akan dibahas.

1. Tentang kognisi secara umum

Ada dua pendekatan untuk kognisi:

Pendekatan Aristoteles . Ini adalah pendekatan holistik dan memperlakukan objek sebagai kotak hitam. Fenomena, objek dipelajari dalam semua realitas secara keseluruhan. Dan kenyataan mengatakan, misalnya, bahwa benda berat jatuh ke tanah lebih cepat daripada yang ringan; yang tersisa bagi dirinya sendiri sebuah tubuh yang bergerak lambat laun berhenti. Pendekatan Aristoteles berkaitan dengan fenomena sebagai realitas integral, oleh karena itu dapat disebut fenomenologis.

Pendekatan Galileo . Ini adalah pendekatan sistem analitik. Ini adalah pendekatan membagi dan menaklukkan. Fenomena, objek diuraikan menjadi bagian-bagian penyusunnya dan masing-masing dipelajari secara terpisah, abstrak dari yang lain (analisis). Kemudian, gambar yang dihasilkan dapat digabungkan menjadi satu, dengan mempertimbangkan interaksi komponen (sintesis). Misalnya, jatuhnya mayat dianggap sebagai jatuhnya mayat di kekosongan. Dan di sana mereka jatuh dengan akselerasi yang sama. Namun pada kenyataannya, gesekan terhadap udara mencegah mereka jatuh sama rata. Setelah mempelajari kekuatan ini secara terpisah, kita dapat menjelaskan hasil Aristoteles. Demikian pula, jika kita melepaskan diri dari gaya gesekan, maka benda yang bergerak akan bergerak tanpa henti. Dan jika kita memperhitungkan gaya gesekan, kita mendapatkan hasil dari Aristoteles. Pendekatan Galileo segera mengarah pada kebutuhan untuk mempelajari kekuatan. Ini, pada akhirnya, diterjemahkan ke dalam sistem fisika klasik yang koheren.

Sekali lagi, untuk kejelasan.

Pendekatan Aristoteles . Ada sebuah fenomena yang sedang diteliti, "Jatuhnya tubuh di udara ke tanah" - fenomena F. Kami mengambil benda yang berbeda dan menemukan bahwa benda yang lebih berat jatuh ke tanah lebih cepat daripada yang ringan.

Pendekatan Galileo . Saat mempelajari fenomena F, seseorang harus memperhitungkan tidak hanya berat badan. Kami mempelajari kejatuhan di udara. Dan mari kita ubah tidak hanya berat badan, tetapi juga udara. Mari kita coba mengurangi kepadatannya, sehingga, pada akhirnya, tidak ada udara. Kemudian kita menemukan bahwa semua tubuh jatuh dalam kekosongan dengan akselerasi yang sama. Kami menemukan parameter pengaruh pada fenomena dan mencoba menciptakan kondisi di mana hanya satu parameter yang signifikan. Ini bukan sifatnya. Oleh karena itu, seorang fisikawan memerlukan laboratorium di mana ia dapat memvariasikan parameter. Setelah mempelajari pengaruh satu parameter, kita dapat melanjutkan untuk mempelajari pengaruh parameter lain. Kami berusaha mengurangi kerumitan keseluruhan pendekatan menjadi komposisi pendekatan yang lebih sederhana. Memvariasikan bentuk tubuh yang jatuh, kita dapat mempelajari ketergantungan gaya gesekan di udara tergantung pada bentuk tubuh. Dengan memvariasikan laju jatuh, kita dapat mendeteksi ketergantungan gaya gesek terhadap kecepatan. Dengan memvariasikan ketinggian musim gugur, kita dapat mendeteksi ketergantungan akselerasi pada ketinggian. Dengan memvariasikan lokasi geografis di bumi, kita menemukan ketergantungan akselerasi jatuh pada geografi.

Secara kasar, dalam pendekatan Aristoteles mereka mempelajari realitas, dan dalam pendekatan Galileo mereka mempelajari abstraksi, dan dari mereka, melalui sintesis, mereka menuju kenyataan.

2. Model pengetahuan fisik

Fisika adalah teori ideal untuk banyak ilmu, termasuk ekonomi. Dalam eksperimen fisik, serangkaian nilai diskrit diperoleh. Tetapi mereka dianggap sebagai perkiraan fungsi kontinu, yang pada kenyataannya adalah indikator fisik. Dan fisikawan mencoba menebak fungsi-fungsi ini. Maka Galileo menebak parabola untuk lintasan sebuah batu yang dilemparkan ke sudut ke cakrawala; Kepler menebak lintasan planet-planet - elips, dll. Setelah menebak lintasan, kami mendapatkan alat prediksi - kemampuan untuk menghitung nilai untuk koordinat lintasan yang belum dijelajahi. Untuk menguji, mereka melakukan percobaan - menciptakan kondisi untuk percobaan yang mendapatkan nilai menarik. Kemudian, setelah memverifikasi nilai prediksi dan nilai eksperimental, kami memperoleh konfirmasi atau bantahan terhadap teori tersebut. Di sini terkadang kesalahan kesalahan eksperimental memainkan peran penting. Pengetahuan fisik diturunkan ke identifikasi determinisme - hukum untuk memperoleh negara dari keadaan awal:

$$

$$S (t) = D (Q, S (0))$$

S(0) -   D –  – ,  S(t)  S(0) Q –       . ,  ,      . 

Jadi, untuk melempar batu dari titik (0,0) dengan kecepatan $$$v_0$secara miring $$$α$ke cakrawala yang kita miliki

$$$$ menampilkan $$ x (t) = v_0 t cos⁡ (α), y (t) = v_0 t sin⁡ (α) - (gt ^ 2) / 2 $$ menampilkan $$

Status awal S (0) diatur oleh tiga parameter: titik keberangkatan (0,0), kecepatan awal $$$v_0$sudut $$$α$.
Dampak lingkungan Q diberikan oleh percepatan gravitasi g. Ketika memperluas ruang lingkup masalah (kecepatan awal yang tinggi) g tidak lagi konstan.
Determinisme D diberikan oleh rumus di atas.

Untuk tugas yang lebih realistis, gesekan terhadap udara harus diperhitungkan. Ini menyulitkan matematika dari masalah, tetapi prinsipnya tetap sama. Alih-alih batu, Anda bisa mempertimbangkan pesawat. Kemudian kekuatan dorong pesawat mulai berlaku, dan pengaturannya oleh pilot. Faktor non-fisik juga muncul - kehendak pilot. Kami tidak dapat memperhitungkannya. Tetapi kita tahu bahwa itu bukan tanpa batas: daya tarik tidak bisa tanpa batas, akselerasi tidak bisa tanpa batas. Ini memperkenalkan unsur kepastian ke dalam gerakan. Mereka menggunakannya, misalnya, untuk membangun lintasan rudal pertahanan udara.

Mari kita kembali ke batu terbang. Ini ditandai dengan jumlah parameter fisik yang tak terbatas. Misalnya, hanya bentuknya saja yang bisa rumit. Tetapi kami yakin bahwa di beberapa area yang bermanfaat kami dapat mempertimbangkan batu sebagai titik material. Ini adalah abstraksi utama dari mekanika klasik. Semua sistem direpresentasikan sebagai set poin materi yang berinteraksi. Hal ini membuat pengurangan kognitif utama - mengurangi perilaku sistem yang kompleks menjadi perilaku komponen-komponen dasarnya.

Sehubungan dengan reduksi kognitif yang disebutkan, dua pendekatan epistemologis dapat dibedakan - reduksionisme dan holisme.

3. Reduksionisme dan holisme

Reduksionisme adalah prinsip pengurangan karakteristik suatu sistem dari karakteristik subsistem dan karakteristik interaksi subsistem. Berhasil bekerja dalam fisika.
Pertimbangkan, misalnya, gas. Tanpa menguraikannya menjadi subsistem, kita dapat beroperasi dengan eksperimen, konsep fenomenologis: tekanan P, suhu T, volume V. Secara empiris, kita menemukan hubungan yang menghubungkan parameter-parameter ini - persamaan keadaan gas:

$$

$$PV = constT$$

Inilah yang disebut tingkat fenomenologis - bekerja dengan fenomena (fenomena) tanpa masuk ke strukturnya. Ini adalah pendekatan Aristoteles.

Sekarang terapkan pendekatan Galileo. Kami menguraikan sistem "gas": bayangkan sebagai kumpulan molekul yang bertabrakan. Kemudian kita mendefinisikan P dan T melalui parameter mekanik molekul. Ini dilakukan dalam fisika molekuler. Jadi, kami mengurangi sistem gas menjadi subsistem molekul. Ini akan memperjelas persamaan negara atau menyimpulkannya untuk sistem baru.

Dengan demikian, dalam bisnis kami memiliki analogi: ekonomi makro didekomposisi menjadi perusahaan dan rumah tangga. Namun di sini pengurangannya belum sempurna. Sayangnya, tidak ada Newton ekonomi. Masalahnya adalah kompleksitas dan ketersediaan faktor subyektif yang tidak ada dalam fisika (meskipun ada perdebatan tentang peran subjek dalam mekanika kuantum).

Dan sekarang tentang holisme.

Holisme adalah prinsip bahwa bisa ada sifat yang tidak dapat direduksi dalam suatu sistem. Jadi dalam biologi, doktrin vitalisme didasarkan pada konsep entelechy, kekuatan hidup yang melekat dalam tubuh secara keseluruhan dan tidak dapat direduksi.

Fisika sejauh ini membuang konsep holisme.

4. Formula dan model algoritmik

Model rumus adalah model yang ditentukan oleh rumus. Konsep "formula" akan dianggap dikenal.

Contoh dalam fisika: persamaan Newton, persamaan Lagrange, persamaan Maxwell, persamaan Navier-Stokes, persamaan Heisenberg-Schrödinger, persamaan Einstein.

Contoh dari ekonomi: formula Black-Scholes untuk harga opsi, formula penawaran uang, model pemrograman linier untuk mengoptimalkan portofolio keuangan, formula perhitungan bunga, formula perhitungan risiko.

Dengan model formula, seseorang dapat bekerja tanpa komputer. Itulah hampir semua matematika murni. Namun di sini, algoritmik memainkan peran yang semakin penting. Jadi solusi untuk masalah empat warna tidak direduksi menjadi formula apa pun, tetapi membutuhkan solusi brute-force untuk banyak kasus khusus. Payudara ini dilakukan oleh komputer.

Model algoritmik - model yang ditentukan oleh suatu algoritma, mungkin tidak dapat direduksi menjadi sebuah formula. Tentu saja, dimungkinkan untuk mengklasifikasikan algoritma sebagai formula, tetapi ini bukan formula klasik yang sama. Model algoritmik awalnya realistis hanya menggunakan komputer
Model formal selalu dapat direduksi menjadi model algoritmik.

Contoh dari model algoritmik pertama adalah masalah Fermi-Pasta-Ulam. Berikut ini kutipan dari buku Ulam, The Adventures of Mathematics.

Dan di sini ada artikel tentang Habré, menceritakan tentang kondisi terkini dari masalah Fermi-Pasta-Ulam:
Matematikawan memecahkan masalah Fermi-Pasta-Ulam

5. Koordinasi

Dengan koordinasi sistem, maksud saya definisi parameter dasar yang, pada prinsipnya, menentukan evolusi sistem. Misalnya, dalam mekanika titik material, koordinasi ditentukan oleh:

• Kekuatan eksternal F
  
  • Titik m massa material
  • Koordinat spasial (x, y, z) = r dari titik material
  • Waktu t

Evolusi sistem diberikan oleh persamaan Newton

$$

$$(d ^ 2 r (t)) / (dt ^ 2) = (F (t)) / m$$

Apa koordinasi entitas ekonomi? Saya pernah bekerja pada sistem intelijen bisnis. Istilah utamanya adalah indikator. Basis sistem adalah kartu skor. Ratusan indikator. Tetapi saya sia-sia mencari di internet untuk deskripsi dasar indikator - seperangkat indikator yang tidak dapat direduksi menjadi yang lain dan, pada prinsipnya, sepenuhnya menentukan evolusi suatu entitas ekonomi. Yaitu, seperti yang saya mengerti, tidak ada koordinasi yang dilakukan dalam ekonomi. Dan, karena itu, berbicara tentang beberapa hukum dasar yang dinamis belum dimungkinkan. Hanya dimungkinkan, berdasarkan koneksi indikator, untuk melakukan analisis skenario - untuk menjawab pertanyaan "Apa yang akan terjadi pada indikator yang diturunkan jika indikator yang mendasarinya akan berubah sesuai dengan skenario yang diberikan?"

6. Contoh abstrak. Peramalan Seri Waktu Seperti Fisika

Anda dapat menanyakan masalah perkiraan berdasarkan deret waktu aktual: memiliki sejumlah nilai nyata, Anda perlu mendapatkan nilai prediksi indikator - nilai di masa mendatang. Ini menyiratkan semacam determinisme tersembunyi dari deret waktu. Ada banyak spekulasi ilmiah dan pseudoscientific tentang hal ini. Saya sendiri berurusan dengan dokter sains yang mengklaim bahwa metodologi mereka akan memungkinkan mereka untuk mendapatkan perkiraan nilai tukar dan menunjukkan disertasi yang sesuai dengan segala macam interval kepercayaan dan atribut lain dari undang-undang distribusi. Tetapi, ketika dihadapkan dengan kenyataan, teknik-teknik itu terhanyut.

Terkadang untuk mendapatkan perkiraan, lakukan ini:

1. Ambil rangkaian waktu nyata {V (ti)}. Jadwal - langkah garis putus-putus.
2. Ambil fungsi kontinu W (t) sedemikian rupa sehingga W (ti) = V (ti). Grafik adalah kurva kontinu.
3. P polinomial (t) dipilih yang mendekati W (t) dengan tingkat akurasi yang memadai. Polinomial dapat dipertimbangkan untuk semua t.
4. Kemudian kami memiliki perkiraan untuk waktu mendatang T: V (T) = P (T)
   Semua ini memberi kesan sains, tetapi hanya pada pandangan pertama. Ya, keberadaan polinomial perkiraan untuk W (t) dijamin oleh teorema Weierstrass dari matanalisis. Kami dapat melakukan polinomisasi secara sewenang-wenang tepatnya W (t). Tapi itu tidak bisa digunakan untuk prediksi.

Nilai perkiraan untuk seri nyata adalah 100%, dan nilai prediktifnya adalah nol. Polinomial dapat ditemukan secara sewenang-wenang, tetapi semuanya akan memberikan perkiraan yang berbeda.

Ketika hari T tiba dan kami menemukan V nyata (T), maka untuk seri {{V (ti)}, V (T)} kita dapat membuat Q polinomial baru (t) yang mendekati deret ini secara sewenang-wenang tepat, tetapi waktu T tidak lagi dalam masa depan dan Q (T) bukan lagi ramalan, tetapi kenyataan. Polinomial P (t) dan Q (t) sama sekali tidak harus bersamaan dan untuk waktu perkiraan baru T '> T mereka akan menunjukkan hasil yang berbeda. Artinya, tidak ada perkiraan. Tampaknya ada sains, tetapi tidak ada ramalan. Itu seperti teori malaikat abad pertengahan. Dia bisa menjelaskan semuanya, tetapi dia tidak bisa memprediksi apa pun.

Perbedaan antara interpolasi fisik dan ekstrapolasi dari ekonomi:

• Keakuratan data empiris : perkiraan dalam fisika, akurat dalam ekonomi
• Fungsi domain : kontinu dalam fisika, terputus-putus, bertahap dalam ekonomi
• Data empiris : dalam fisika, diskrit, ekonomi terus menerus dengan diskontinuitas diskrit
• Hukum dasar : dalam fisika ada. F = ma, misalnya; dalam ekonomi belum

7. Ekonomi dan fisika

Dalam ilmu ekonomi, lintasan nyata - pada dasarnya diskontinyu - adalah fungsi yang konstan konstan. Misalnya, indikator "Nilai tukar" dapat membuat lompatan kapan saja. Fungsi ekonomi berkelanjutan - perkiraan demi matanalisis (jika Anda memiliki palu di tangan Anda, maka Anda ingin mempertimbangkan objek apa pun seperti paku ...). Setiap transaksi akuntansi menyebabkan lonjakan nilai indikator derivatif dari akun. Dan mereka adalah mayoritas indikator. Selanjutnya, setiap perubahan dalam jumlah pekerja terpisah, dll. Kelangsungan lintasan ekonomi berbeda dengan kelanjutan sebagian besar lintasan fisik. Oleh karena itu, peralatan matanalisis tidak secara langsung berlaku untuk lintasan ekonomi.

Gambar untuk kognisi fisik. Lintasan batu dilemparkan pada sudut ke cakrawala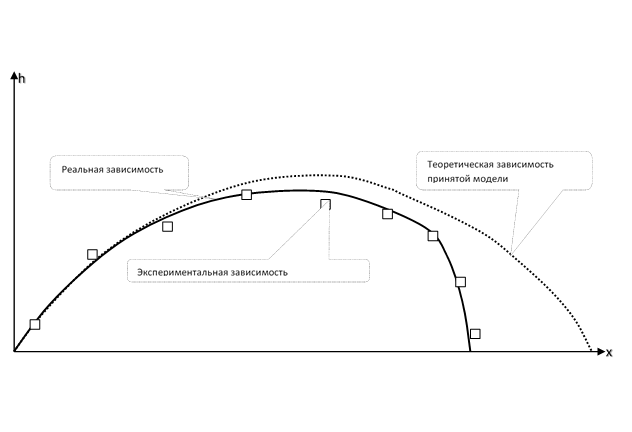

Gambar untuk pengetahuan ekonomi. Nilai tukar mata uang di bank sentral.

Ini adalah fungsi eksak eksperimental yang nyata. Ini terputus pada titik waktu ketika nilai tukar berubah.

Dalam fisika:

• Nilai fisik eksperimental hampir selalu merupakan perkiraan
• Nilai fisik eksperimental membentuk serangkaian diskrit.
• Serangkaian diskrit eksperimental dianggap sebagai poligon untuk pendekatan kontinu karena kenyataan kontinu. Konsep kontinuitas dapat berubah menjadi kebohongan pada skala spasial dan temporal yang kecil. Maka fisika akan mengubah wajahnya.
• Indikator dasar yang terdefinisi dengan baik
• Lintasan teoretis dan nyata hampir selalu kontinu dan hampir selalu dapat dibedakan (lintasan titik material selalu dua kali dapat dibedakan dalam waktu)
• Karena kontinuitas dinamika nyata dan lintasan nyata, pendekatan kontinu yang baik memiliki kekuatan prediksi: dalam lingkungan yang cukup kecil, fungsi tidak akan jauh dari nilai riil terakhirnya.

Dalam perekonomian:

• Nilai ekonomi eksperimental dapat dianggap akurat. Hanya dalam ekonomi makro ada masalah akurasi karena banyaknya entitas bisnis.
• Nilai ekonomi eksperimental terdiri dari interval keteguhan, terputus pada titik-titik tertentu ketika nilai berubah secara tiba-tiba
• Data eksperimental tidak dapat dianggap sebagai tempat pengujian untuk perkiraan kontinu karena kenyataan terputus-putus.
• Indikator dasar tidak sepenuhnya ditentukan. Tidak jelas mengapa menari.
• Karena diskontinuitas lintasan nyata, setiap pendekatan berkelanjutan yang sewenang-wenang yang baik tidak menjamin prediksi di lingkungan kecil yang sewenang-wenang.
• Lintasan nyata hampir selalu terputus. Ini berarti bahwa tekad ekonomi memerlukan pendekatan yang berbeda dari mekanika klasik.
• Dalam perekonomian, pada awalnya ada faktor kehendak bebas suatu entitas ekonomi. Kisarannya diatur oleh negara. Batas ekstrim kebebasan ini:
  - Kebebasan penuh dalam pasar yang tidak diatur oleh negara
  - Kebebasan sebagian di pasar yang sebagian diatur oleh negara
  - Tidak adanya kebebasan di negara yang sepenuhnya tersentralisasi dimana tidak ada pasar bebas

Pengetahuan ekonomi belum mencapai tingkat yang mirip dengan mekanika klasik:

1. Komponen dasar dari jenis titik material tidak didefinisikan
2. Tidak didefinisikan Q (parameter lingkungan), tidak jelas apa yang penting, apa yang tidak
3. Stratifikasi sistem ekonomi yang terperinci belum dilakukan,
4. Proses reduksi tidak jelas dan apakah mungkin; hukum determinisme ekonomi tidak jelas.

. – . – . ? , . . . . , – .

, . , , - .

8. IT

8.1.

. . . . , . . . . . . . , , . . … , . . , . . . , . . . . . . . . . . . – " . - "!? , . -1840( , ). . . , . , . , . , . . , , . (). . , , , : ", . ". ! . , , - .

8.2. -

. — . , , .. . . , . . – . , . , . – . . …

. . , . , , , . , . . . . . , - . . . . , : , . . . , , . . ? . . , .

. - , .

, , . , . . , .

. . . , . , . , : , . , . . .

, – Jump Processing. , . .

, . “ ”. , – . , , . – , . . , – .

8.3.

( ). . “”. . , . , . . – . . , . . . . , . . – . . , . … . ? , . , - . . . , . , , . . .

. , . , . , – . , . , – ( – ?).

8.4.

_{“ ”}

. () . . . , , . . , . . , , . . . – . , , . , . . , . Bagus . – . , . – . . , (, ). , . . , . . , , , . . . – . . . . . . . . . : , , , , , , , , … . 100 . ( , , ) . , ( , (SQL-) ). , . Yaitu . . . , . . , : ”, . . . ”.

. , . , . : . , , .

. . . , , . . . . -.

() . , , ( ), . , . , – . , , , , , . . . , , . , “” “”. , “” “”. ? , .

: . . . , . . . . — . . : . : , …

. . , . . .

, . . - . . — . Kenapa ini? .

: IT. .