Kami melanjutkan ke perhitungan fungsi logis menurut grafik untuk kelas perilaku yang lebih luas. Kami menganggap perilaku otonom siklik yang tidak mengandung banyak sinyal (atau dengan cara lain: tidak mengandung peristiwa yang diindeks). Batasan lain: untuk kenyamanan, kami tidak akan mempertimbangkan koneksi cabang paralel di OR. Kami menganggap hanya koneksi oleh AND, yaitu, suatu peristiwa dipicu hanya ketika semua peristiwa pendahulunya dipicu.
Kami akan menggunakan STG untuk menggambarkan perilaku, tetapi dengan batasan tambahan. Untuk setiap tempat, jumlah busur yang masuk dan keluar sama dengan masing-masing satu. Dengan demikian, tempat dengan busur masuk dan keluar dapat dianggap sebagai satu busur yang menghubungkan dua peristiwa (transisi). Dengan demikian, penandaan bergerak di sepanjang busur. Karena perilaku dengan banyak sinyal tidak dipertimbangkan sekarang, indeks peristiwa dilarang, mereka tidak diperlukan. Acara kosong dilarang. Situasi ini juga dilarang ketika dua busur yang termasuk dalam satu peristiwa keluar dari peristiwa yang tidak sejajar satu sama lain (kasus khusus berasal dari peristiwa yang sama). Tujuan dari ini adalah untuk menghilangkan busur yang tidak membawa muatan semantik. Selebihnya dianggap benar (normal, hidup, aman) dari sudut pandang perilaku STG, dengan mempertimbangkan batasan di atas. Perilaku tidak mengandung konflik CSC.
Definisi 1. Peristiwa di mana busur masuk adalah konsekuensi dari peristiwa dari mana busur ini keluar. Sebaliknya, peristiwa dari mana busur keluar adalah penyebab peristiwa di mana busur ini masuk.
Definisi 2. Sebuah jalur - urutan kejadian tanpa akhir - hasil dari perubahan dalam pelabelan grafik, dimulai dengan yang spesifik. Setiap peristiwa memasuki urutan jumlah kali yang tak terbatas. Setiap entri tersebut unik.
Definisi 3. Jejak peristiwa A adalah jalur di mana semua peristiwa merupakan konsekuensi langsung dari peristiwa A, atau hasil dari penutupan transitif dari hubungan konsekuensi dari peristiwa sehubungan dengan peristiwa A. Penandaan awal untuk jejak peristiwa A ditetapkan sebagai berikut. Jika penandaan diubah secara sewenang-wenang, setelah peristiwa A dipicu, penanda di output busur peristiwa A diperbaiki. Kemudian sisa marker bergerak hingga pergerakan marker menjadi tidak mungkin tanpa melepaskan marker pada output busur acara A. Penandaan yang dihasilkan adalah penandaan awal untuk jejak peristiwa A.
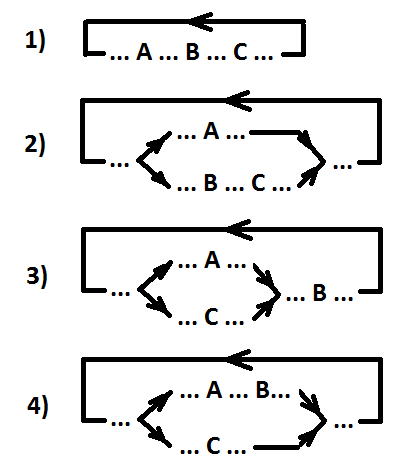
Definisi 4. Kami memperkenalkan relasi pemesanan untuk tiga acara (A, B, C). Tiga peristiwa diperintahkan (ditulis A> B> C) jika dan hanya jika, untuk setiap jejak peristiwa A, kejadian pertama peristiwa B dalam urutan akan selalu terjadi lebih awal daripada kejadian pertama peristiwa C.
Komentar. Peristiwa A dapat paralel dengan kedua peristiwa B dan C (atau hanya C), atau kedua peristiwa A dan B dapat paralel dengan peristiwa C.
Opsi lokasi untuk acara yang dipesan A, B, dan C (A> B> C).
Definisi 5. Sinyal b (switching B1 dan B2) mengambil sinyal a (switching A1 dan A2) berkenaan dengan peristiwa X dan Y (peristiwa X dan Y adalah paralel atau bertepatan) jika kondisi berikut ini benar:
1) X> A1> A2;
2) jika event A2 sejajar dengan event X dan tidak sejajar dengan event Y, maka X> A2> Y;
3) Y> B1> B2;
4) jika event B2 sejajar dengan event Y dan tidak sejajar dengan event X, maka Y> B2> X;
5) Y> B1> A2;
6) jika event A2 sejajar dengan event Y dan tidak sejajar dengan event X, maka Y> A2> X.
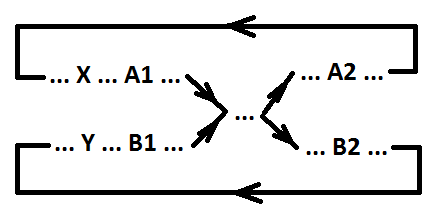
Keterangan 1. Kondisi 1, 2, dan 3, 4 menentukan urutan perpindahan sinyal a dan b, masing-masing. Ketentuan 5, 6 menentukan urutan kejadian tangkapan B1 dan kejadian tangkapan A2.
Komentar 2. Acara X dapat menjadi acara A1. Dalam hal ini, kondisi 1 dan 2 merosot.
Keterangan 3. Acara Y dapat menjadi acara B1. Dalam hal ini, kondisi 3, 4, dan 5 merosot.
Komentar 4. Event X dapat menjadi event A1, dan juga event B1 dapat menjadi event Y. Dalam hal ini, kondisi 1, 2, 3, 4, dan 5 mengalami degenerasi.
Sekarang kita mulai mempertimbangkan apa itu implan. Implan dicirikan oleh peristiwa, sebagai akibatnya implan mengubah maknanya.
Definisi 6. Suatu peristiwa, sebagai akibatnya AND (OR) yang implant mengubah nilainya dari 1 (0) menjadi 0 (1), kita akan memanggil batas kanan dari implan. Sinyal yang sesuai dengan acara ini akan disebut dinyalakan. Implan menyala.
Definisi 7. Suatu peristiwa, sebagai akibatnya AND (OR) yang implant mengubah nilainya dari 0 (1) menjadi 1 (0), kita akan memanggil batas kiri dari implan. Sinyal yang sesuai dengan acara ini akan dimatikan. Implan mati.
Definisi 8. Implant di mana dua kanan (atau dua kiri) batas tidak sejajar satu sama lain akan disebut diskontinyu.
Untuk saat ini, kami tidak akan mempertimbangkan implan yang terganggu. Kami akan kembali ke pertimbangan mereka di bawah ini.
Jadi, kita memiliki: semua batas kanan implan berpasangan sejajar satu sama lain, serta batas kiri implan berpasangan sejajar satu sama lain.
Properti penting. Implan menyala ketika setidaknya satu peristiwa terjadi, yang merupakan batas kanan implant. Implan mati hanya ketika semua peristiwa yang merupakan batas kiri dari implan terjadi.
Sekarang tinggal mengidentifikasi sifat-sifat sinyal yang membentuk implan.
Definisi 9. Sinyal yang termasuk dalam implan akan disebut variabel.
Properti variabel pertama. Menghidupkan dan mematikan sinyal adalah variabel.
Properti variabel kedua. Untuk setiap variabel switching (salah satu sakelar yang merupakan batas kiri dari L implant, yang lain adalah beberapa peristiwa X), harus ada suatu peristiwa - beberapa batas kanan R dari implan yang sama adalah sedemikian rupa sehingga baik X dan R adalah peristiwa yang sama, atau R > X> L.
Properti variabel ketiga. Untuk setiap variabel inklusif (salah satu sakelar yang merupakan batas kanan R implant, yang lain adalah beberapa peristiwa X), harus ada suatu peristiwa - beberapa batas kiri L dari implan yang sama adalah sedemikian rupa sehingga baik X dan L adalah peristiwa yang sama, atau R > X> L.
Properti variabel keempat. Untuk variabel apa pun (switching X1 dan X2) yang tidak menyalakan atau mematikan, harus ada dua peristiwa: beberapa batas kiri L implant dan beberapa batas kanan R implant sehingga R> X1> L dan R> X2> L . Jika tidak, implan tidak dapat mempertahankan nilai konstan dalam posisi tidak aktif.
Properti variabel kelima. Untuk setiap pasangan: beberapa variabel switching dan beberapa variabel switching, harus ada urutan variabel yang saling mengambil sehubungan dengan beberapa batas kanan implan (untuk pickup yang berbeda, batas kanan dapat bervariasi), dimulai dengan variabel switching ini dan berakhir dengan variabel switching ini. . Jika tidak, implan tidak dapat mempertahankan nilai konstan pada posisi aktif.
Properti variabel keenam. Untuk setiap variabel inklusif a, jika batas kanan implan adalah peristiwa a + (a-), maka variabel tersebut termasuk dalam catatan implan AND (OR) dengan inversi, dan dalam catatan implan OR (dan AND) tanpa inversi. Untuk setiap variabel switching a, jika batas kiri implant adalah peristiwa a- (a +), maka variabel tersebut dimasukkan dalam rekaman implant AND (OR) dengan inversi, dan dalam rekaman implant OR (DAN) tanpa inversi.
Properti variabel ketujuh. Berdasarkan sifat keempat dari variabel, untuk setiap variabel a yang tidak menyala atau mati, ada batas kanan untuk implant R dan batas kiri untuk implant L sehingga R> a +> L dan R> a-> L. Jika R> a +> a-, maka variabel seperti itu memasukkan implant dari Dan dengan inversi, dan implant dari OR tanpa inversi. Jika R> a-> a +, maka variabel tersebut memasuki AND dan tanpa inversi, dan OR implant dengan inversi.
Tujuh properti variabel yang terdaftar adalah properti yang diperlukan dari implan. Juga, sifat-sifat ini cukup untuk menggambarkan implan.
Komentar. Deskripsi implan di atas tidak melarang situasi ketika beberapa batas kiri implan dapat sejajar dengan beberapa batas kanan implan yang sama. Arti dari fenomena ini adalah bahwa, tergantung pada kecepatan proses paralel, implan tersebut secara real time dapat menjadi opsional untuk implementasi sinyal yang sesuai dan secara real time mungkin tidak mati (jika batas kanan bekerja lebih awal dari batas kiri).
Sekarang kita akan mempertimbangkan bagaimana bentuk normal dari fungsi logis dibangun dari implan.
Definisi 10. Jika untuk beberapa keadaan, implan berada pada posisi tidak aktif (nilai implan AND (OR) adalah 1 (0)), kami mengatakan bahwa implan mencakup keadaan ini.
Pertimbangkan sinyal x tertentu, untuk itu kita perlu menghitung fungsi logis. Untuk membangun DNF (CNF), maka perlu AND (OR) -implicants mencakup semua status di mana fungsi x adalah 1 (0). Dalam hal ini, adalah penting bahwa tidak satupun dari AND (OR) -implicants ini yang mencakup kondisi di mana fungsi x adalah 0 (1). Juga, ketika menghitung fungsi logis, perlu untuk mempertimbangkan spesifikasi sirkuit: implan harus “tumpang tindih”. Artinya, jika dalam beberapa keadaan implan dapat dihidupkan (yaitu, suatu peristiwa yang merupakan batas kanan implan ini dapat dipicu) dan nilai fungsi sinyal x tidak berubah selama perpindahan ini, maka harus ada implan lain yang mencakup keadaan ini dan tidak menyala saat acara ini dipicu.
Sekarang kita perlu mengklarifikasi tiga pertanyaan. Apa yang dimaksud dengan keadaan dalam bentuk grafik? Bagaimana menentukan status di mana fungsi sinyal x adalah 1 (0)? Bagaimana cara menentukan kondisi yang dicakup oleh implan?
Mari kita mulai dengan negara. Segala pelabelan yang dapat dicapai adalah syarat. Karena tidak ada konflik CSC, setiap label yang dapat dicapai sesuai dengan keadaan unik (dapat dicapai). Di negara-negara yang tidak dapat dijangkau, nilai fungsi bersifat arbitrer dan tidak perlu mempertimbangkannya. Dengan demikian, setiap negara yang kami anggap secara unik dijelaskan oleh label yang sesuai. Posisi setiap penanda secara unik ditentukan oleh busur yang ditandainya. Setiap busur secara unik terkait dengan sepasang peristiwa (dipesan): peristiwa dari mana busur keluar dan peristiwa di mana busur masuk. Dengan demikian, setiap keadaan yang dapat dicapai secara unik dijelaskan oleh satu set yang terdiri dari pasangan peristiwa yang teratur.
Definisi 11. Sepasang peristiwa yang menunjukkan busur bertanda akan ditulis {P, S}, di mana P adalah peristiwa penyebabnya, dan S adalah peristiwa akibatnya.
Definisi 12. MM akan disebut himpunan pasangan berurutan {P, S}, yang menggambarkan beberapa keadaan yang dapat dicapai.
Sekarang mari kita tentukan yang menyatakan nilai fungsi x adalah 1, dan untuk mana itu adalah 0. Biarkan peristiwa x + disebabkan oleh n peristiwa A1, A2, ..., An, dan peristiwa x- disebabkan oleh m peristiwa B1, B2, ..., Bm.
Nilai fungsi x adalah 1 jika:
atau 1) untuk setiap i dari 1 hingga n, pasangan {Ai, x +} milik MM yang ditetapkan;
atau 2) pasangan {x +, S} sedemikian rupa sehingga x +> S> x- milik MM yang ditetapkan;
atau 3) pasangan {P, S} sedemikian rupa sehingga x +> P> x- dan x +> S> x- milik MM yang ditetapkan;
atau 4) pasangan {P, x-} sedemikian rupa sehingga x +> P> x- milik MM yang ditetapkan dan terdapat i dari 1 hingga m sehingga pasangan {Bi, x-} tidak termasuk dalam MM yang ditetapkan.
Nilai fungsi x adalah 0 jika:
atau 1) untuk setiap i dari 1 hingga m, pasangan {Bi, x-} milik MM yang ditetapkan;
atau 2) pasangan {x-, S} sedemikian rupa sehingga x-> S> x + milik MM yang ditetapkan;
atau 3) pasangan {P, S} sedemikian sehingga x-> P> x + dan x-> S> x + milik MM set;
atau 4) pasangan {P, x +} sedemikian rupa sehingga x-> P> x + milik MM yang ditetapkan dan terdapat i dari 1 hingga n sehingga pasangan {Ai, x +} tidak termasuk dalam MM yang ditetapkan.
Sekarang kita mengetahui kondisi apa yang dicakup implan. Biarkan implan memiliki n batas kiri L1, L2, ..., Ln dan m batas kanan R1, R2, ..., Rm.
Implan tidak mencakup keadaan yang dijelaskan oleh himpunan MM jika setidaknya salah satu pasangan {P, S} milik set MM memenuhi kondisi berikut: ada i dari 1 ke n dan j dari 1 ke m sedemikian rupa sehingga
1) Li dan S adalah acara yang sama dan Rj> P> Li,
atau 2) Rj dan P adalah acara yang sama dan Rj> S> Li,
atau 3) Rj> P> Li dan Rj> S> Li.
Pernyataan ini benar berdasarkan properti kelima variabel.
Implan mencakup keadaan yang dijelaskan oleh himpunan MM jika tidak ada pasangan {P, S} yang dimiliki oleh himpunan MM kondisi berikut dipenuhi: ada i dari 1 ke n dan j dari 1 ke m sedemikian rupa sehingga
1) Li dan S adalah acara yang sama dan Rj> P> Li,
atau 2) Rj dan P adalah acara yang sama dan Rj> S> Li,
atau 3) Rj> P> Li dan Rj> S> Li.
Pernyataan ini benar berdasarkan sifat variabel kedua, ketiga, dan keempat.
Berbicara secara kiasan, sebuah implan mencakup negara jika semua penanda berada di antara batas kiri dan kanan implan. Jika setidaknya satu penanda terletak di luar batas ini, maka implan tidak mencakup keadaan ini.
Sekarang kami memiliki alat untuk menghitung bentuk normal (masih belum jelas, namun, masih ada pertanyaan dengan implan intermiten). Tapi kami tertarik pada bentuk normal minimal (dengan mempertimbangkan spesifikasi sirkuit). Sebelum melangkah lebih jauh, mari kita kembali ke pertimbangan implan intermiten. Pertimbangkan I-implant untuk sinyal DNF x (kasus dengan OR-implant untuk CNF serupa). Misalkan dua batas kiri dari implan yang sama L1 dan L2 tidak sejajar satu sama lain dan L1> L2> x- (kasus untuk dua batas kanan dianggap sama). Maka harus ada dua batas kanan dari implan R1 dan R2 sehingga untuk pasangan L1 dan R2, dan L2 dan R1, sifat kedua, ketiga, keempat dan kelima dari variabel harus dipenuhi. Jika ada batas kiri L3 yang sejajar dengan L1, maka untuk pasangan L3 dan R2, properti di atas juga harus dipenuhi (sama, dalam hal adanya batas yang sesuai, implan yang sejajar dengan batas L2, R1 dan R2). Tetapi, karena banyak sinyal tidak digunakan, harus ada implan non-diskontinyu dengan batas L1 dan R2 (dan dengan batas paralel yang sesuai, jika ada implan terputus memilikinya). Selain itu, implan non-diskontinyu terdiri dari variabel yang lebih sedikit dan mencakup semua keadaan yang dicakup oleh implan diskontinyu, di mana fungsi sinyal x memiliki nilai 1. Oleh karena itu kesimpulan: implan diskontinyu bukan ekstrem dan tidak dapat digunakan untuk menghitung fungsi minimal.
Lebih lanjut tentang menghitung fungsi minimal di bagian selanjutnya.