Pendekatan serakah dan mesin slot. Analisis tugas ML-track kejuaraan pemrograman

Kami terus mempublikasikan analisis tugas yang diusulkan di kejuaraan baru-baru ini. Baris berikutnya adalah tugas yang diambil dari babak kualifikasi untuk spesialis pembelajaran mesin. Ini adalah trek ketiga dari empat (backend, frontend, ML, analytics). Peserta perlu membuat model untuk memperbaiki kesalahan ketik dalam teks, mengusulkan strategi untuk bermain di mesin slot, mengingatkan sistem rekomendasi untuk konten, dan menyusun beberapa program lagi.

A. Kesalahan Pengetikan

Ketentuan

(epigraf) (dari satu forum)
- Siapa yang menyusun omong kosong ini?
- Ahli astrofisika. Mereka juga manusia.
- Anda membuat 10 kesalahan dalam kata "jurnalis".

Banyak pengguna membuat kesalahan pengetikan, beberapa karena menekan tombol, dan beberapa karena buta huruf. Kami ingin memeriksa apakah pengguna benar-benar dapat mengingat kata lain selain yang diketiknya.

Secara lebih formal, anggaplah bahwa model kesalahan berikut terjadi: pengguna mulai dengan kata yang ingin ia tulis, dan kemudian membuat sejumlah kesalahan di dalamnya. Setiap kesalahan adalah substitusi dari beberapa substring kata untuk substring lain. Satu kesalahan terkait dengan mengganti hanya dalam satu posisi (yaitu, jika pengguna ingin membuat kesalahan tunggal dengan aturan "abc" → "cba", maka dari string "abcabc" ia bisa mendapatkan "cbaabc" atau "abccba"). Setelah setiap kesalahan, proses berulang. Aturan yang sama dapat digunakan beberapa kali dalam langkah yang berbeda (misalnya, dalam contoh di atas, "cbacba" dapat diperoleh dalam dua langkah).

Hal ini diperlukan untuk menentukan jumlah kesalahan minimum yang dapat dilakukan pengguna jika ia memikirkan satu kata tertentu dan menulis yang lain.

Solusi

Mari kita coba untuk menghasilkan dari ejaan yang benar semua kata yang mungkin dengan tidak lebih dari 4 kesalahan. Dalam kasus terburuk, mungkin ada O ((L﹒N) ⁴ ). Dalam batasan masalah, ini adalah angka yang agak besar, jadi Anda perlu mencari cara untuk mengurangi kompleksitas. Alih-alih, Anda dapat menggunakan algoritme meet-in-the-middle: menghasilkan kata-kata dengan tidak lebih dari 2 kesalahan, serta kata-kata dari mana Anda bisa mendapatkan kata yang ditulis pengguna tanpa lebih dari 2 kesalahan. Perhatikan bahwa ukuran masing-masing set ini tidak akan melebihi 10 ⁶ . Jika jumlah kesalahan yang dilakukan oleh pengguna tidak melebihi 4, maka set ini akan berpotongan. Demikian pula, kami dapat memverifikasi bahwa jumlah kesalahan tidak melebihi 3, 2, dan 1.

 struct FromTo { std::string from; std::string to; }; std::pair<size_t, std::string> applyRule(const std::string& word, const FromTo &fromTo, int pos) { while(true) { int from = word.find(fromTo.from, pos); if (from == std::string::npos) { return {std::string::npos, {}}; } int to = from + fromTo.from.size(); auto cpy = word; for (int i = from; i < to; i++) { cpy[i] = fromTo.to[i - from]; } return {from, std::move(cpy)}; } } void inverseRules(std::vector<FromTo> &rules) { for (auto& rule: rules) { std::swap(rule.from, rule.to); } } int solve(std::string& wordOrig, std::string& wordMissprinted, std::vector<FromTo>& replaces) { std::unordered_map<std::string, int> mapping; std::unordered_map<int, std::string> mappingInverse; mapping.emplace(wordOrig, 0); mappingInverse.emplace(0, wordOrig); mapping.emplace(wordMissprinted, 1); mappingInverse.emplace(1, wordMissprinted); std::unordered_map<int, std::unordered_set<int>> edges; auto buildGraph = [&edges, &mapping, &mappingInverse](int startId, const std::vector<FromTo>& replaces, bool dir) { std::unordered_set<int> mappingLayer0; mappingLayer0 = {startId}; for (int i = 0; i < 2; i++) { std::unordered_set<int> mappingLayer1; for (const auto& v: mappingLayer0) { auto& word = mappingInverse.at(v); for (auto& fromTo: replaces) { size_t from = 0; while (true) { auto [tmp, wordCpy] = applyRule(word, fromTo, from); if (tmp == std::string::npos) { break; } from = tmp + 1; { int w = mapping.size(); mapping.emplace(wordCpy, w); w = mapping.at(wordCpy); mappingInverse.emplace(w, std::move(wordCpy)); if (dir) { edges[v].emplace(w); } else { edges[w].emplace(v); } mappingLayer1.emplace(w); } } } } mappingLayer0 = std::move(mappingLayer1); } }; buildGraph(0, replaces, true); inverseRules(replaces); buildGraph(1, replaces, false); { std::queue<std::pair<int, int>> q; q.emplace(0, 0); std::vector<bool> mask(mapping.size(), false); int level{0}; while (q.size()) { auto [w, level] = q.front(); q.pop(); if (mask[w]) { continue; } mask[w] = true; if (mappingInverse.at(w) == wordMissprinted) { return level; } for (auto& v: edges[w]) { q.emplace(v, level + 1); } } } return -1; } 

B. Bandit berlengan banyak

Ketentuan

Ini adalah tugas interaktif.

Anda sendiri tidak tahu bagaimana itu terjadi, tetapi Anda mendapati diri Anda berada di aula dengan mesin slot dengan seluruh kantong token. Sayangnya, di box office, mereka menolak untuk menerima token kembali, dan Anda memutuskan untuk mencoba keberuntungan Anda. Ada banyak mesin slot di aula yang bisa Anda mainkan. Untuk satu game dengan mesin slot Anda menggunakan satu token. Jika menang, mesin memberi Anda satu dolar, jika terjadi kerugian - tidak ada. Setiap mesin memiliki probabilitas tetap untuk menang (yang Anda tidak tahu), tetapi berbeda untuk mesin yang berbeda. Setelah mempelajari situs web produsen mesin ini, Anda menemukan bahwa probabilitas menang untuk setiap mesin dipilih secara acak pada tahap pembuatan dari distribusi beta dengan parameter tertentu.

Anda ingin memaksimalkan kemenangan yang Anda harapkan.

Solusi

Masalah ini sudah diketahui, bisa diselesaikan dengan berbagai cara. Keputusan utama juri menerapkan strategi pengambilan sampel Thompson , tetapi karena jumlah langkah diketahui pada awal program, ada strategi yang lebih optimal (misalnya, UCB1). Selain itu, seseorang bahkan bisa bertahan dengan strategi epsilon-serakah: dengan probabilitas tertentu ε memainkan mesin acak dan dengan probabilitas (1 - ε) memainkan mesin dengan statistik kemenangan terbaik.

 class SolverFromStdIn(object): def __init__(self): self.regrets = [0.] self.total_win = [0.] self.moves = [] class ThompsonSampling(SolverFromStdIn): def __init__(self, bandits_total, init_a=1, init_b=1): """ init_a (int): initial value of a in Beta(a, b). init_b (int): initial value of b in Beta(a, b). """ SolverFromStdIn.__init__(self) self.n = bandits_total self.alpha = init_a self.beta = init_b self._as = [init_a] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self._bs = [init_b] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self.last_move = -1 random.seed(int(time.time())) def move(self): samples = [random.betavariate(self._as[x], self._bs[x]) for x in range(self.n)] self.last_move = max(range(self.n), key=lambda x: samples[x]) self.moves.append(self.last_move) return self.last_move def set_reward(self, reward): i = self.last_move r = reward self._as[i] += r self._bs[i] += (1 - r) return i, r while True: n, m = map(int, sys.stdin.readline().split()) if n == 0 and m == 0: break alpha, beta = map(float, sys.stdin.readline().split()) solver = ThompsonSampling(m) for _ in range(n): print >> sys.stdout, solver.move() + 1 sys.stdout.flush() reward = int(sys.stdin.readline()) solver.set_reward(reward) 

C. Penyelarasan kalimat

Ketentuan

Salah satu tugas paling penting untuk melatih model terjemahan mesin yang baik adalah kasus kalimat paralel yang baik. Biasanya, sumber untuk penawaran paralel adalah dokumen paralel. Ternyata seringkali untuk membangun korpus kalimat paralel tertentu, Anda tidak perlu tahu apa-apa selain panjangnya. Secara khusus, Anda mungkin memperhatikan bahwa semakin lama kalimat dalam bahasa sumber, semakin lama kemungkinan akan diterjemahkan. Beberapa kesulitan terletak pada kenyataan bahwa selama terjemahan jumlah kalimat dalam teks dapat berubah: kadang-kadang dua kalimat yang berdekatan dalam terjemahan dapat digabungkan menjadi satu, atau sebaliknya - satu kalimat dapat dibagi menjadi dua. Dalam beberapa kasus yang jarang terjadi, kalimat dapat dihilangkan seluruhnya dalam terjemahan, atau terjemahan mungkin muncul dalam terjemahan yang tidak asli.

Lebih formal, anggap model generatif berikut untuk penutup paralel adalah benar. Pada setiap langkah, kami melakukan salah satu dari yang berikut:

1. Berhenti

Dengan probabilitas p _h, generasi lambung berakhir.

2. [1-0] Melewati penawaran

Dengan probabilitas p _{d kita} menganggap satu kalimat ke teks asli. Kami tidak menghubungkan apa pun dengan terjemahan. Panjang kalimat dalam bahasa asli L ≥ 1 dipilih dari distribusi diskrit:

.

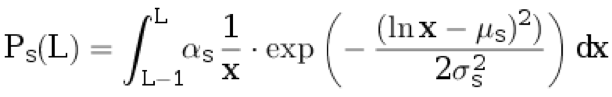
Di sini μ _s , σ _s adalah parameter distribusi, dan α _s adalah koefisien normalisasi yang dipilih .

3. [0-1] Masukkan proposal

Dengan probabilitas p _{i, kami} menetapkan satu kalimat untuk terjemahan. Kami tidak menganggap apa pun dari aslinya. Panjang kalimat dalam bahasa terjemahan L ≥ 1 dipilih dari distribusi diskrit:

.

Di sini μ _t , σ _t adalah parameter distribusi, dan α _t adalah koefisien normalisasi yang dipilih .

4. Terjemahan

Dengan probabilitas (1 - p _d - p _i - p _h ) kami mengambil panjang kalimat dalam bahasa asli L _s ≥ 1 dari distribusi p _s (dengan pembulatan ke atas). Selanjutnya, kami menghasilkan panjang kalimat dalam bahasa terjemahan _Lt ≥ 1 dari distribusi diskrit bersyarat:

.

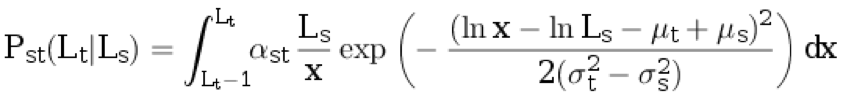
Di sini, α _st adalah koefisien normalisasi, dan parameter yang tersisa dijelaskan dalam paragraf sebelumnya.

Berikutnya adalah langkah lain:

1. [2-1] Dengan probabilitas p _{split s,} kalimat yang dihasilkan dalam bahasa asli terbagi menjadi dua yang tidak kosong, sehingga jumlah total kata bertambah tepat satu . Probabilitas bahwa kalimat dengan panjang Ls _akan terpisah menjadi bagian-bagian dengan panjang L1 dan L2 (yaitu, L1 + L2 = Ls + 1) sebanding dengan Ps (L ₁ ) ⋅ Ps (L ₂ ).

2. [1-2] Dengan probabilitas p _{split t,} kalimat yang dihasilkan dalam bahasa target dibagi menjadi dua kalimat yang tidak kosong, sehingga jumlah total kata bertambah tepat satu. Probabilitas bahwa kalimat dengan panjang _{Lt akan} terpecah menjadi beberapa bagian dengan panjang L1 dan L2 (yaitu, L1 + L2 = _Lt + 1) sebanding dengan _Pt (L1) ⋅ Pt (L ₂ ).

3. 3. [1-1] Dengan probabilitas (1 - _{pisah s} - p _{split t} ), tidak satu pun dari pasangan kalimat yang dihasilkan akan meluruh.

Solusi

Tugas ini merupakan kasus penyelarasan khusus menggunakan model Markov tersembunyi (penyelarasan HMM). Gagasan utamanya adalah Anda dapat menghitung probabilitas menghasilkan sepasang dokumen tertentu menggunakan model ini dan algoritma penerusan : dalam kasus ini, negara adalah sepasang awalan dokumen. Dengan demikian, probabilitas yang diperlukan untuk menyelaraskan pasangan kalimat paralel tertentu dapat dihitung dengan algoritma maju-mundur .

D. Rekaman rekomendasi

Ketentuan

Pertimbangkan umpan rekomendasi untuk konten heterogen. Ini mencampur objek dari berbagai jenis (gambar, video, berita, dll.). Objek-objek ini biasanya dipesan berdasarkan relevansinya dengan pengguna: semakin relevan (menarik) objek dengan pengguna, semakin dekat ke bagian atas daftar rekomendasi. Namun, dengan pemesanan seperti itu, situasi sering muncul di mana beberapa objek dari jenis yang sama muncul dalam daftar rekomendasi. Ini sangat memperburuk variasi eksternal dari rekomendasi kami dan oleh karena itu pengguna tidak menyukainya. Diperlukan untuk mengimplementasikan suatu algoritma yang, sesuai dengan daftar rekomendasi, akan membuat daftar baru yang akan bebas dari masalah ini dan akan menjadi yang paling relevan.

Biarkan daftar rekomendasi awal diberi = [a ₀ , a ₁ , ..., a _{n - 1} ] dengan panjang n> 0. Objek dengan angka i memiliki tipe dengan angka b _i ∈ {0, ..., m - 1}. Selain itu, objek di bawah angka i memiliki relevansi r (a _i ) = 2 _−i . Pertimbangkan daftar yang diperoleh dari yang awal dengan memilih subset objek dan mengatur ulang mereka: x = [a _{i 0} , a _{i 1} , ..., a _{i k - 1} ] dengan panjang k (0 ≤ k ≤ n). Daftar disebut dapat diterima jika tidak ada dua objek berurutan di dalamnya bertepatan dengan tipe, mis., B _{i j} ≠ b _{i j + 1} untuk semua j = 0, ..., k - 2. Relevansi daftar dihitung oleh rumus $$$\ sum_ {j = 0} ^ {k-1} 2 _ {- j} r (a_ {i_j})$. Anda perlu menemukan daftar relevansi maksimum di antara semua yang valid.

Solusi

Dengan menggunakan perhitungan matematis sederhana, dapat ditunjukkan bahwa masalahnya dapat diselesaikan dengan pendekatan "serakah", yaitu, dalam daftar rekomendasi yang optimal, setiap item memiliki objek paling relevan dari semua yang valid pada awal daftar yang sama. Implementasi dari pendekatan ini sederhana: kita mengambil objek dalam satu baris dan menambahkannya ke jawabannya, jika memungkinkan. Ketika objek yang tidak valid ditemukan (jenis yang bertepatan dengan jenis yang sebelumnya), kami mengesampingkannya dalam antrian terpisah, dari mana kami memasukkannya ke dalam respons sesegera mungkin. Perhatikan bahwa pada setiap saat, semua objek dalam antrian ini akan memiliki jenis yang cocok. Pada akhirnya, beberapa objek mungkin tetap dalam antrian, mereka tidak akan lagi dimasukkan dalam respons.

  std::vector<int> blend(int n, int m, const std::vector<int>& types) { std::vector<int> result; std::queue<int> repeated; for (int i = 0; i < n; ++i) { if (result.empty() || types[result.back()] != types[i]) { result.push_back(i); if (!repeated.empty() && types[repeated.front()] != types[result.back()]) { result.push_back(repeated.front()); repeated.pop(); } } else { repeated.push(i); } } return result; } 

D. Klasterisasi urutan karakter

Ada alfabet terbatas A = {a ₁ , a ₂ , ..., a _{K - 1} , a _K = S}, a _i ∈ {a, b, ..., z}, S adalah akhir dari baris.

Pertimbangkan metode berikut untuk menghasilkan string acak di atas alfabet A:

1. Karakter pertama x ₁ adalah variabel acak dengan distribusi P (x ₁ = a _i ) = q _i (diketahui bahwa q _K = 0).
2. Setiap karakter berikutnya dihasilkan berdasarkan yang sebelumnya sesuai dengan distribusi kondisional P (x _i = a _j | | x _{i - 1} = a _l ) = p _jl .
3. Jika x _i = S, generasi berhenti dan hasilnya x ₁ x ₂ ... x _{i - 1} .

Himpunan garis yang dihasilkan dari campuran dua model yang dijelaskan dengan parameter yang berbeda diberikan. Adalah perlu untuk setiap baris untuk memberikan indeks rantai dari mana ia dihasilkan.

Solusi

Masalah diselesaikan dengan menggunakan algoritma EM : diasumsikan bahwa sampel yang disajikan dihasilkan dari campuran dua rantai Markov yang parameternya dipulihkan selama iterasi. Pembatasan 80% dari jawaban yang benar dibuat sehingga kebenaran solusi tidak terpengaruh oleh contoh-contoh yang memiliki probabilitas tinggi di kedua rantai. Contoh-contoh ini, oleh karena itu, ketika dipulihkan dengan benar, dapat ditugaskan ke rantai yang tidak benar dalam hal respons yang dihasilkan.

 import random import math EPS = 1e-9 def empty_row(size): return [0] * size def empty_matrix(rows, cols): return [empty_row(cols) for _ in range(rows)] def normalized_row(row): row_sum = sum(row) + EPS return [x / row_sum for x in row] def normalized_matrix(mtx): return [normalized_row(r) for r in mtx] def restore_params(alphabet, string_samples): n_tokens = len(alphabet) n_samples = len(string_samples) samples = [tuple([alphabet.index(token) for token in s] + [n_tokens - 1, n_tokens - 1]) for s in string_samples] probs = [random.random() for _ in range(n_samples)] for _ in range(200): old_probs = [x for x in probs] # probs fixed p0, A = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) q0, B = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) for prob, sample in zip(probs, samples): p0[sample[0]] += prob q0[sample[0]] += 1 - prob for t1, t2 in zip(sample[:-1], sample[1:]): A[t1][t2] += prob B[t1][t2] += 1 - prob A, p0 = normalized_matrix(A), normalized_row(p0) B, q0 = normalized_matrix(B), normalized_row(q0) trans_log_diff = [ [math.log(b + EPS) - math.log(a + EPS) for b, a in zip(B_r, A_r)] for B_r, A_r in zip(B, A) ] # A, p0, B, q0 fixed probs = empty_row(n_samples) for i, sample in enumerate(samples): value = math.log(q0[sample[0]] + EPS) - math.log(p0[sample[0]] + EPS) for t1, t2 in zip(sample[:-1], sample[1:]): value += trans_log_diff[t1][t2] probs[i] = 1.0 / (1.0 + math.exp(value)) if max(abs(x - y) for x, y in zip(probs, old_probs)) < 1e-9: break return [int(x > 0.5) for x in probs] def main(): N, K = list(map(int, input().split())) string_samples = [] alphabet = list(input().strip()) + [''] for _ in range(N): string_samples.append(input().rstrip()) result = restore_params(alphabet, string_samples) for r in result: print(r) if __name__ == '__main__': main() 

---

.