Algoritma Collapse Wavefunction mengajarkan komputer untuk berimprovisasi. Pada input, ia menerima data pola dasar dan membuat data yang dihasilkan secara prosedural mirip dengan yang asli.
( Sumber )Paling sering digunakan untuk membuat gambar, tetapi juga dapat membangun
kota ,
skatepark dan menulis
puisi yang mengerikan .
( Sumber )Runtuhnya fungsi gelombang adalah algoritma yang sangat independen yang hampir tidak memerlukan bantuan atau instruksi dari luar. Anda hanya perlu contoh gaya yang ingin Anda capai, dan dia akan melakukan sisanya. Terlepas dari kemandiriannya, ia ternyata sederhana. Itu tidak menggunakan jaringan saraf, hutan acak, atau apa pun yang menyerupai pembelajaran mesin. Jika Anda berurusan dengan ide itu, itu akan menjadi sangat dimengerti dan intuitif untuk Anda.
Sebagian besar implementasi dan penjelasan tentang runtuhnya fungsi gelombang adalah versi algoritma yang lengkap dan dioptimalkan dengan cepat. Tentu saja, semua itu penting dan perlu, tetapi sulit untuk memahaminya dari awal. Dalam posting ini, saya akan menjelaskan semuanya dalam bahasa sederhana yang saya pahami, dengan fokus pada versi terbatas Wavefunction, yang saya sebut
Even Simpler Tiled Model . Selain itu, saya memposting
contoh implementasi ESTM di Github . Kode di dalamnya tidak efisien dan lambat, tetapi sangat mudah dibaca dan dikomentari secara rinci. Segera setelah Anda memahami teknologi yang mendasari ESTM, Anda akan menjadi lebih dekat untuk memahami versi algoritma yang lebih kompleks. Jika Anda ingin memahami algoritma runtuhnya fungsi gelombang, maka artikel ini akan menjadi awal yang baik.
Mari kita mulai dengan ceritanya.
Pernikahan
Bayangkan Anda merencanakan pernikahan Anda. Selain pilihan perhiasan dan musik, Anda perlu membuat rencana tempat duduk untuk tamu untuk makan malam. Keluarga Anda suka berdebat dan nakal, jadi itu bisa sulit. Seorang ayah tidak bisa duduk lebih dekat dari dua meja dari ibunya. Sepupu menjadi kesepian jika dia tidak duduk dengan sepupu lainnya. Dan lebih baik tidak menanam Paman Roy di sebelah anggota keluarga pasangan Anda yang ramah lingkungan. Tetap hanya 5 jam sebelum kedatangan makanan, jadi Anda memutuskan untuk menyerang tugas keras kepala ini menggunakan algoritma keruntuhan fungsi gelombang.
Anda mulai dengan daftar panjang aturan dan rencana tempat duduk kosong.
Anda membuat
fungsi gelombang asli
dari paket. Dia mengikat setiap kursi ke daftar orang yang dapat duduk di atasnya. Sementara setiap orang bisa duduk di kursi apa saja. Fungsi gelombang tamu tempat duduk dimulai dengan
superposisi lengkap (konsep ini dipinjam dari fisika kuantum) dari setiap skema yang mungkin.
Kucing Schrödinger mati dan hidup pada saat yang sama sampai seseorang membuka kotak itu dan memeriksa; rencana Anda pada saat yang sama setiap skema yang mungkin sampai Anda membereskan semuanya. Superposisi lengkap adalah gagasan teoretis yang berguna, tetapi itu tidak akan membantu nenek Anda menentukan di mana dia harus duduk. Anda perlu membawa fungsi gelombang lokasi para tamu ke satu keadaan tertentu, yang kemudian dapat diubah menjadi kartu nama biasa, non-kuantum.
Kami mulai melakukan ini dengan melakukan
runtuhnya fungsi gelombang untuk satu kursi. Kami memilih kursi, melihat daftar orang yang dapat duduk di atasnya, dan secara acak menugaskannya kepada salah satu dari mereka. Dalam hal ini, fungsi gelombang tinja menjadi runtuh.
Pilihan ini memiliki konsekuensi memperluas ke fungsi gelombang kursi yang tersisa. Jika Paman Roy duduk di meja 2, maka sepupu Frank dan Michelle Obama (teman keluarga pasangan Anda) pasti tidak akan di sebelahnya. Dan jika Michelle tidak duduk di meja 2, maka Barack juga tidak akan berada di belakangnya. Kami memperbarui fungsi gelombang dari rencana lokasi dengan menghapus orang dari daftar kandidat yang memungkinkan.
Segera setelah getaran diselesaikan, kami mengulangi proses ini. Kami memilih kursi lain dengan beberapa kandidat yang memungkinkan dan menutup fungsi gelombangnya, secara acak memilih salah satu orang yang dapat diterima. Sekali lagi, kami memperluas getaran yang disebabkan oleh pilihan ini ke seluruh rencana, menghilangkan orang dari fungsi gelombang kursi jika mereka tidak bisa lagi duduk di atasnya.
Kami mengulangi proses ini baik sampai fungsi gelombang runtuh (yaitu, persis 1 orang yang duduk tetap di dalamnya), atau sampai kami mencapai
kontradiksi . Kontradiksi adalah kursi yang tidak dapat diduduki oleh siapa pun, karena mereka semua diusir karena pemilihan sebelumnya. Kontradiksi membuat ketidakmungkinan runtuhnya seluruh fungsi gelombang.
Jika Anda telah mencapai kontradiksi, maka cara termudah adalah memulai dari awal. Buang semua pekerjaan sebelumnya, temukan rencana kosong baru dan mulai algoritme lagi, selesaikan runtuhnya fungsi gelombang untuk kursi acak lainnya. Anda juga dapat menerapkan sistem backtracking yang memungkinkan Anda untuk membatalkan pilihan tertentu, daripada segera meninggalkan segalanya ("bagaimana jika Sheila dipindahkan ke kursi 54?").
Setelah beberapa kesalahan dimulai, Anda akhirnya akan mencapai keadaan benar-benar runtuh di mana setiap kursi ditugaskan tepat satu orang dan semua aturan diikuti. Selesai!
Dari pernikahan hingga bitmap
Ini bukan contoh teoretis. Anda benar-benar dapat mewujudkan varian runtuhnya fungsi gelombang, yang akan membuat rencana tempat duduk untuk tamu untuk pernikahan. Namun, dalam Wavefunction Collapse yang lebih tradisional, kami biasanya mencoba untuk tidak menempatkan orang di pesta pernikahan, tetapi untuk mengatur piksel dalam gambar output. Namun, prosesnya akan sangat mirip. Kami mengajarkan algoritma seperangkat aturan yang harus dipenuhi oleh output. Kami menginisialisasi fungsi gelombang. Kami melakukan keruntuhan satu elemen dan memperluas konsekuensinya ke seluruh fungsi gelombang. Dan kami terus melakukannya, baik sampai fungsi gelombang benar-benar runtuh, atau sampai kami mencapai kontradiksi.
Runtuhnya fungsi gelombang tradisional berbeda dari keruntuhan pernikahan dalam cara kami mengajarkan algoritma aturan yang harus diikuti. Dalam versi pernikahan, kami harus menuliskan sendiri peraturannya. Namun dalam versi tradisional, kami hanya memberikan algoritma contoh gambar, dan berdasarkan itu, algoritma menciptakan sisanya. Dia mem-parsing contoh, menganalisis polanya dan mencari tahu bagaimana pixel atau
ubin harus sejajar.
Mari kita mulai meneliti runtuhnya fungsi gelombang dengan melihat kasus khusus sederhana, yang
ExUtumno (pencipta algoritma) dengan
Model Ubin Sederhana .
Model ubin sederhana
Dalam Model Ubin Sederhana, gambar input dan output dibangun dari sejumlah kecil ubin yang telah ditentukan, dan setiap kotak dalam gambar output dibatasi hanya untuk empat tetangga terdekatnya. Misalnya, kita menghasilkan dunia acak untuk gim dua dimensi dengan tampilan teratas. Kita dapat memiliki ubin untuk daratan, pantai dan laut, serta seperangkat aturan seperti "pantai bisa dekat laut", "tanah bisa dekat pantai" dan "laut bisa di sebelah laut lain".
Model Ubin Sederhana memperhitungkan simetri dan rotasi ubinnya. Misalnya, tanah mungkin dekat pantai, tetapi hanya dalam orientasi yang benar.
Pemrosesan simetri ini memberikan gambar output yang lebih baik, tetapi menyulitkan kode. Untuk menjaga hal-hal sederhana, mari kita melihat pandangan yang lebih sederhana tentang runtuhnya fungsi gelombang, yang saya sebut
Even Simpler Tiled Model .
Bahkan Model Ubin Lebih Sederhana
Bahkan Model Ubin Simpler (“model ubin yang bahkan lebih sederhana”) mirip dengan Model Ubin Sederhana, tetapi ubinnya tidak memiliki sifat simetri. Setiap ubin memiliki satu piksel dengan warna yang sama, artinya, kami tidak akan dapat mengacaukan tepinya dengan cara apa pun.
Bahkan aturan Model Ubin Sederhana menentukan ubin mana yang dapat ditempatkan bersebelahan dan di mana orientasi. Setiap aturan adalah tupel dari tiga elemen (3-tuple): dua ubin dan satu arah. Misalnya,
(SEA, COAST, LEFT) berarti bahwa ubin
SEA (laut) dapat
dari ubin
COAST (pantai). Aturan ini harus disertai dengan aturan lain yang menggambarkan situasi dalam hal
COAST -
(COAST, SEA, RIGHT) .
Jika Anda ingin ubin
SEA berada tidak hanya untuk
, tetapi juga untuk
dari ubin
COAST . maka mereka membutuhkan aturan tambahan:
(SEA, COAST, RIGHT) dan
(COAST, SEA, LEFT) .
Seperti yang saya katakan di atas, kita tidak perlu membuat daftar semua aturan ini sendiri. Runtuhnya fungsi gelombang dapat membuat seperangkat aturan untuk Model Even Simpler Tile dengan mem-parsing contoh gambar dan mengumpulkan daftar semua 3-tupel yang dikandungnya.
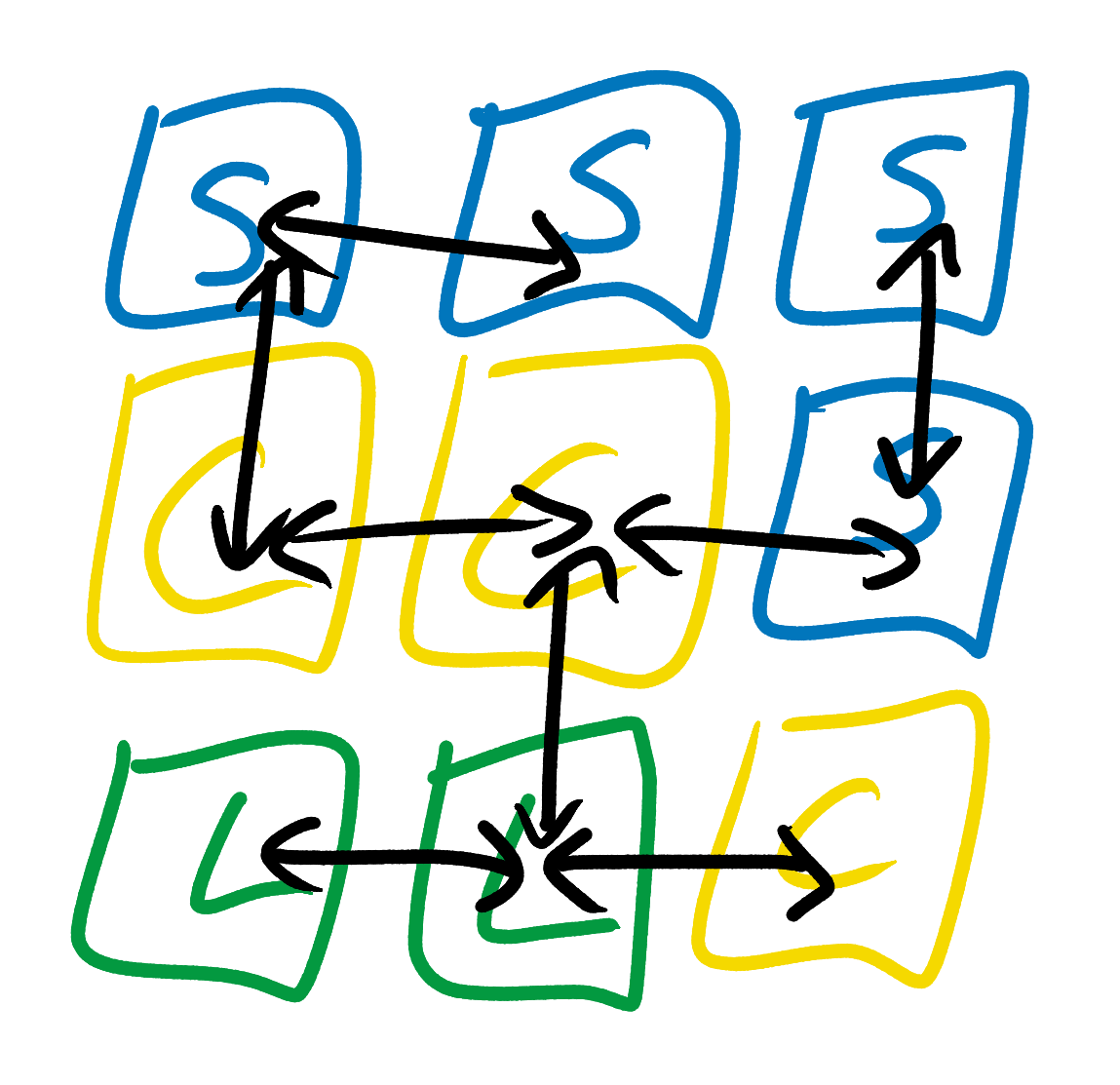
Setelah memeriksa contoh gambar yang ditunjukkan di atas, Even Tile Model Simpler memperhatikan bahwa ubin laut hanya bisa berada di bawah atau ke sisi ubin pantai, atau di mana saja di dekat ubin laut lainnya. Dia juga mencatat bahwa ubin pantai dapat ditempatkan di sebelah tanah, laut, atau ubin pantai lainnya, tetapi hanya di atas ubin laut dan di bawah ubin tanah. Dia tidak mencoba untuk mendapatkan aturan yang lebih kompleks, misalnya, "ubin laut harus dekat setidaknya satu ubin laut" atau "setiap pulau harus mengandung setidaknya satu ubin tanah." Tidak ada ubin yang dapat memengaruhi fakta bahwa beberapa jenis ubin dapat atau tidak dapat ditemukan dua kotak atau lebih dari mereka. Ini mirip dengan model rencana pernikahan di mana satu-satunya aturan adalah: "X bisa duduk di sebelah Y".
Saat menganalisis gambar yang masuk, kita juga perlu merekam frekuensi pertemuan setiap ubin. Kemudian, kita menggunakan angka-angka ini sebagai bobot ketika memilih fungsi gelombang kotak, yang keruntuhannya harus dilakukan, dan juga ketika memilih ubin yang ditugaskan ke kotak ketika itu runtuh.
Setelah mempelajari aturan yang harus dipatuhi gambar keluaran, kami siap membangun runtuhnya fungsi gelombang dari gambar keluaran.
Runtuh
Seperti dalam contoh pernikahan, kami memulai proses keruntuhan dengan fungsi gelombang di mana setiap kuadrat gambar output berada di superposisi setiap jenis ubin.
Kita mulai dengan memilih kotak yang fungsi gelombangnya akan runtuh. Dalam contoh pernikahan, pilihan ini dibuat secara kebetulan. Namun, seperti yang dicatat
ExUtumno , orang biasanya melakukan tugas-tugas ini secara berbeda. Sebaliknya, mereka mencari kotak dengan
entropi terendah. Entropi adalah ukuran ketidakpastian dan gangguan. Secara umum, kotak dengan entropi tinggi adalah kotak dengan banyak ubin yang tersisa dalam fungsi gelombangnya. Masih belum jelas ubin mana dia akhirnya runtuh. Kotak entropi rendah adalah kotak dengan ubin paling sedikit dalam fungsi gelombang. Himpunan ubin, yang salah satunya runtuh, sudah sangat terbatas.
Misalnya, dalam Model Even Simpler Tile, kotak tanpa informasi tentang kotak di sekitarnya tidak terbatas dan dapat menjadi ubin apa pun. Karena itu, ia memiliki entropi yang sangat tinggi. Tetapi sebuah kotak di mana beberapa kotak telah runtuh dapat memiliki pilihan hanya 2 ubin.
Fungsi gelombang dari alun-alun pusat pada gambar di atas tidak sepenuhnya runtuh, tetapi kita sudah tahu bahwa itu tidak bisa menjadi ubin tanah. Namun, ini sudah terbatas, yang berarti memiliki
entropi lebih rendah daripada kuadrat kanan atas, yang masih bisa berupa daratan, laut, atau pantai.
Ini adalah ubin terbatas dengan entropi rendah sehingga orang biasanya memperhatikan ketika mereka secara manual menyelesaikan masalah tersebut. Bahkan jika Anda tidak menggunakan runtuhnya fungsi gelombang untuk membuat rencana untuk menempatkan tamu di pesta pernikahan dan akan menyusunnya sendiri, tetap fokus pada area rencana yang sudah memiliki jumlah pembatasan terbesar. Anda tidak akan menempatkan Dwayne di tabel 1, dan kemudian secara acak melompat untuk mendapatkan Katie di tabel 7 (yang sejauh ini kosong). Anda pertama-tama meletakkan Dwayne, lalu Anda akan mencari tahu siapa yang bisa duduk di sebelahnya, lalu siapa yang bisa duduk di sebelah orang ini, dan seterusnya. Saya belum melihat adanya pembenaran untuk ini, tetapi intuisi saya mengatakan bahwa menggunakan
heuristik dengan entropi minimal ini cenderung menghasilkan lebih sedikit
kontradiksi daripada jika Anda secara acak memilih kotak untuk runtuh.
Rumus Shannon digunakan sebagai rumus entropi dalam algoritma runtuhnya fungsi gelombang. Itu menggunakan bobot ubin yang kami parsing dari gambar yang masuk pada langkah sebelumnya:
# Sums are over the weights of each remaining # allowed tile type for the square whose # entropy we are calculating. shannon_entropy_for_square = log(sum(weight)) - (sum(weight * log(weight)) / sum(weight))
Setelah menghitung kuadrat fungsi gelombang dengan entropi terkecil, kami menutup fungsi gelombangnya. Kami melakukan ini dengan memilih secara acak salah satu ubin yang masih tersedia untuk kuadrat, ditimbang oleh bobot ubin yang kami parsing dari gambar yang masuk. Bobot digunakan karena memberikan gambar keluaran yang lebih realistis. Misalkan fungsi gelombang dari sebuah bujur sangkar melaporkan bahwa ia dapat berupa daratan atau pantai. Kami tidak selalu harus memilih salah satu opsi dengan probabilitas 50%. Jika gambar input memiliki lebih banyak ubin tanah daripada pantai, maka kita harus mencerminkan keunggulan ini dalam gambar output. Ini diwujudkan dengan menggunakan bobot global sederhana. Jika dalam contoh gambar ada
20 ubin tanah dan
10 ubin pantai, maka kuadrat runtuh menjadi tanah dengan probabilitas
2/3 , dan di pantai dengan probabilitas tersisa
1/3 .
Kemudian kita memperluas konsekuensi dari pilihan ke fungsi gelombang keluaran lainnya ("jika ubin itu ternyata laut, maka ubin ini tidak bisa menjadi daratan, artinya, ini bukan pantai"). Ketika semua tremor ini telah menetap, kami mengulangi proses menggunakan heuristik entropi minimum untuk memilih ubin runtuh berikutnya. Kami mengulangi siklus propagasi runtuh ini, baik sampai seluruh fungsi gelombang gambar output benar-benar runtuh dan kami dapat mengembalikan hasilnya, atau sampai kami mencapai kontradiksi dan mengembalikan kesalahan.
Akibatnya, kami menciptakan dunia (atau kesalahan).
Ke mana harus pergi selanjutnya
Setelah berurusan dengan Even Tiles Model Bahkan, Anda siap untuk menaiki tangga kekuatan dan kompleksitas algoritma. Mulailah dengan Model Ubin Sederhana yang kami sebutkan di awal posting ini, kemudian lanjutkan ke Model Tumpang tindih penuh. Dalam Model Tumpang tindih, ubin atau piksel saling mempengaruhi dari jarak jauh. Jika Anda memahami hal-hal seperti itu, maka
ExUtumno memperhatikan bahwa Model Ubin Sederhana mirip dengan rantai Markov pesanan-1, dan model yang lebih kompleks menyerupai rantai pesanan yang lebih besar.
Kerusakan Fungsi Gelombang bahkan dapat memperhitungkan batasan tambahan akun, misalnya, "ubin ini harus berupa laut" atau "piksel ini harus berwarna merah" atau "hanya ada satu monster dalam output". Semua ini dijelaskan dalam
README dari proyek utama . Anda juga dapat mempelajari optimasi kecepatan yang dilakukan untuk implementasi penuh. Tidak perlu menghitung ulang entropi dari setiap kotak di setiap iterasi, dan penyebaran informasi dengan fungsi gelombang dapat dilakukan lebih cepat. Aspek-aspek ini menjadi lebih penting karena ukuran gambar output meningkat.
Runtuhnya fungsi gelombang adalah alat yang indah dan kuat yang layak dikuasai. Pikirkan tentang hal itu lain kali Anda merencanakan pernikahan atau menghasilkan dunia prosedural.