Dalam bab ini, saya memberikan penjelasan sederhana dan sebagian besar visual dari teorema universalitas. Untuk mengikuti materi dalam bab ini, Anda tidak harus membaca yang sebelumnya. Ini disusun sebagai esai independen. Jika Anda memiliki pemahaman paling dasar tentang NS, Anda harus dapat memahami penjelasannya.
Salah satu fakta paling menakjubkan tentang jaringan saraf adalah mereka dapat menghitung fungsi apa pun. Artinya, katakanlah seseorang memberi Anda semacam fungsi kompleks dan berliku f (x):
Dan terlepas dari fungsi ini, ada jaminan jaringan saraf sehingga untuk setiap input x nilai f (x) (atau beberapa perkiraan dekat dengan itu) akan menjadi output dari jaringan ini, yaitu:
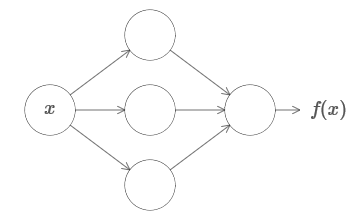
Ini berfungsi bahkan jika itu adalah fungsi dari banyak variabel f โโ= f (x
1 , ..., x
m ), dan dengan banyak nilai. Sebagai contoh, di sini adalah jaringan yang menghitung suatu fungsi dengan m = 3 input dan n = 2 output:
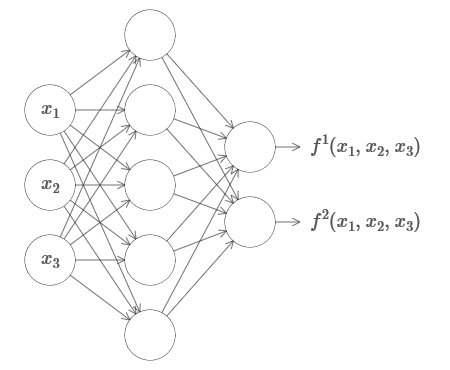
Hasil ini menunjukkan bahwa jaringan saraf memiliki universalitas tertentu. Tidak peduli apa fungsi yang ingin kita hitung, kita tahu bahwa ada jaringan saraf yang bisa melakukan ini.
Selain itu, teorema universalitas berlaku bahkan jika kita membatasi jaringan pada satu lapisan antara neuron yang masuk dan keluar - yang disebut dalam satu lapisan tersembunyi. Jadi, bahkan jaringan dengan arsitektur yang sangat sederhana pun bisa sangat kuat.
Teorema universalitas dikenal oleh orang-orang yang menggunakan jaringan saraf. Tetapi meskipun demikian, pemahaman tentang fakta ini tidak begitu luas. Dan sebagian besar penjelasan untuk ini terlalu rumit secara teknis. Sebagai contoh,
salah satu makalah pertama yang membuktikan hasil ini menggunakan
teorema Hahn - Banach ,
teorema representasi Riesz , dan beberapa analisis Fourier. Jika Anda seorang ahli matematika, mudah bagi Anda untuk memahami bukti ini, tetapi bagi kebanyakan orang itu tidak mudah. Sayang sekali, karena alasan dasar universalitas itu sederhana dan indah.
Dalam bab ini, saya memberikan penjelasan sederhana dan sebagian besar visual dari teorema universalitas. Kami akan melangkah langkah demi langkah melalui ide-ide yang melatarbelakanginya. Anda akan mengerti mengapa jaringan saraf benar-benar dapat menghitung fungsi apa pun. Anda akan memahami beberapa batasan dari hasil ini. Dan Anda akan memahami bagaimana hasilnya dikaitkan dengan NS yang mendalam.
Untuk mengikuti materi dalam bab ini, Anda tidak harus membaca yang sebelumnya. Ini disusun sebagai esai independen. Jika Anda memiliki pemahaman paling dasar tentang NS, Anda harus dapat memahami penjelasannya. Namun saya terkadang akan memberikan tautan ke materi sebelumnya untuk membantu mengisi kesenjangan pengetahuan.
Teorema universalitas sering ditemukan dalam ilmu komputer, jadi terkadang kita bahkan lupa betapa menakjubkannya mereka. Tapi ada baiknya mengingatkan diri sendiri: kemampuan untuk menghitung fungsi sewenang-wenang benar-benar luar biasa. Hampir setiap proses yang dapat Anda bayangkan dapat direduksi menjadi penghitungan suatu fungsi. Pertimbangkan tugas menemukan nama komposisi musik berdasarkan pada bagian singkat. Ini dapat dianggap sebagai penghitungan fungsi. Atau pertimbangkan tugas menerjemahkan teks berbahasa Mandarin ke bahasa Inggris. Dan ini dapat dianggap sebagai penghitungan fungsi (pada kenyataannya, banyak fungsi, karena ada banyak opsi yang dapat diterima untuk menerjemahkan satu teks). Atau pertimbangkan tugas menghasilkan deskripsi plot film dan kualitas akting berdasarkan file mp4. Ini juga dapat dianggap sebagai penghitungan fungsi tertentu (pernyataan yang dibuat tentang opsi terjemahan teks juga benar di sini). Universalitas berarti bahwa, pada prinsipnya, NS dapat melakukan semua tugas ini, dan banyak lainnya.
Tentu saja, hanya dari fakta bahwa kita tahu bahwa ada NS yang mampu, misalnya, menerjemahkan dari Bahasa Mandarin ke Bahasa Inggris, tidak berarti kita memiliki teknik yang baik untuk membuat atau bahkan mengenali jaringan semacam itu. Pembatasan ini juga berlaku untuk teorema universalitas tradisional untuk model seperti skema Boolean. Tetapi, seperti yang telah kita lihat dalam buku ini, NS memiliki algoritma yang kuat untuk fungsi pembelajaran. Kombinasi dari algoritma pembelajaran dan fleksibilitas adalah campuran yang menarik. Sejauh ini, dalam buku ini, kami telah berkonsentrasi pada algoritma pelatihan. Dalam bab ini, kita akan fokus pada keserbagunaan dan apa artinya.
Dua trik
Sebelum menjelaskan mengapa teorema universalitas itu benar, saya ingin menyebutkan dua trik yang terkandung dalam pernyataan informal โjaringan saraf dapat menghitung fungsi apa punโ.
Pertama, ini tidak berarti bahwa jaringan dapat digunakan untuk menghitung fungsi apa pun secara akurat. Kita hanya bisa mendapatkan perkiraan sebaik yang kita butuhkan. Dengan meningkatkan jumlah neuron tersembunyi, kami meningkatkan aproksimasi. Sebagai contoh, saya sebelumnya menggambarkan jaringan yang menghitung fungsi tertentu f (x) menggunakan tiga neuron tersembunyi. Untuk sebagian besar fungsi, menggunakan tiga neuron, hanya perkiraan berkualitas rendah yang dapat diperoleh. Dengan meningkatkan jumlah neuron tersembunyi (katakanlah, hingga lima), kita biasanya bisa mendapatkan perkiraan yang lebih baik:
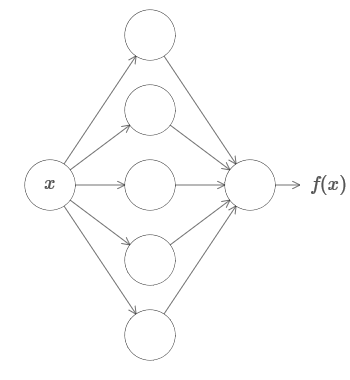
Dan untuk memperbaiki situasi dengan meningkatkan jumlah neuron tersembunyi lebih lanjut.
Untuk memperjelas pernyataan ini, katakanlah kita diberi fungsi f (x), yang ingin kita hitung dengan akurasi yang diperlukan ฮต> 0. Ada jaminan bahwa ketika menggunakan jumlah neuron tersembunyi yang cukup, kita selalu dapat menemukan NS yang outputnya g (x) memenuhi persamaan | g (x) โf (x) | <ฮต untuk setiap x. Dengan kata lain, perkiraan akan dicapai dengan akurasi yang diinginkan untuk setiap nilai input yang memungkinkan.
Tangkapan kedua adalah bahwa fungsi yang dapat diperkirakan dengan metode yang dijelaskan adalah milik kelas kontinu. Jika fungsi terputus, yaitu, ia membuat lompatan tajam tiba-tiba, maka dalam kasus umum tidak mungkin untuk mendekati dengan bantuan NS. Dan ini tidak mengejutkan, karena NS kami menghitung fungsi input data yang berkelanjutan. Namun, bahkan jika fungsi yang benar-benar perlu kita hitung adalah diskontinyu, perkiraannya seringkali cukup kontinu. Jika demikian, maka kita dapat menggunakan NS. Dalam praktiknya, batasan ini biasanya tidak penting.
Akibatnya, pernyataan yang lebih akurat dari teorema universalitas adalah bahwa NS dengan satu lapisan tersembunyi dapat digunakan untuk memperkirakan setiap fungsi kontinu dengan akurasi yang diinginkan. Dalam bab ini, kami membuktikan versi yang sedikit kurang keras dari teorema ini, menggunakan dua lapisan tersembunyi, bukan satu. Dalam tugas, saya akan menjelaskan secara singkat bagaimana penjelasan ini dapat disesuaikan, dengan perubahan kecil, menjadi bukti yang hanya menggunakan satu lapisan tersembunyi.
Fleksibilitas dengan satu input dan satu nilai output
Untuk memahami mengapa teorema universalitas itu benar, kita mulai dengan memahami cara membuat fungsi perkiraan NS hanya dengan satu input dan satu nilai output:
Ternyata inilah esensi dari tugas universalitas. Setelah kami memahami kasus khusus ini, akan sangat mudah untuk memperluasnya ke fungsi dengan banyak nilai input dan output.
Untuk membuat pemahaman tentang bagaimana membangun jaringan untuk menghitung f, kita mulai dengan jaringan yang mengandung lapisan tersembunyi tunggal dengan dua neuron tersembunyi, dan dengan lapisan keluaran yang mengandung satu neuron keluaran:
Untuk membayangkan bagaimana komponen jaringan bekerja, kami fokus pada neuron tersembunyi atas. Dalam diagram di
artikel asli, Anda dapat secara interaktif mengubah berat dengan mouse dengan mengklik "w" dan segera melihat bagaimana fungsi yang dihitung oleh perubahan neuron tersembunyi atas:
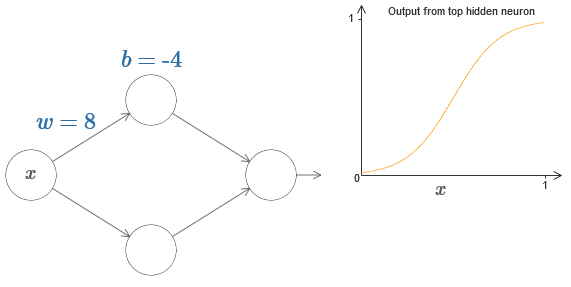
Seperti yang kita pelajari sebelumnya dalam buku ini, neuron tersembunyi menghitung ฯ (wx + b), di mana ฯ (z) โก 1 / (1 + e
โz ) adalah
sigmoid . Sejauh ini, kami cukup sering menggunakan bentuk aljabar ini. Namun, untuk membuktikan universalitas, akan lebih baik jika kita mengabaikan aljabar ini sepenuhnya, dan sebaliknya memanipulasi dan mengamati bentuk pada grafik. Ini tidak hanya akan membantu Anda lebih merasakan apa yang terjadi, tetapi juga memberi kami bukti universalitas yang berlaku untuk fungsi aktivasi lainnya selain sigmoid.
Sebenarnya, pendekatan visual yang saya pilih secara tradisional tidak dianggap sebagai bukti. Tetapi saya percaya bahwa pendekatan visual memberikan lebih banyak wawasan tentang kebenaran hasil akhir daripada bukti tradisional. Dan, tentu saja, pemahaman seperti itu adalah tujuan nyata dari buktinya. Dalam bukti yang saya usulkan, celah kadang-kadang akan muncul; Saya akan memberikan bukti visual yang masuk akal, tetapi tidak selalu ketat. Jika ini mengganggu Anda, maka anggap tugas Anda untuk mengisi kekosongan ini. Namun, jangan lupa tujuan utama: untuk memahami mengapa teorema universalitas itu benar.
Untuk memulai dengan bukti ini, klik pada offset b pada diagram asli dan seret ke kanan untuk memperbesarnya. Anda akan melihat bahwa dengan peningkatan offset, grafik bergerak ke kiri, tetapi tidak berubah bentuk.
Kemudian seret ke kiri untuk mengurangi offset. Anda akan melihat bahwa grafik bergerak ke kanan tanpa mengubah bentuk.
Kurangi berat badan menjadi 2-3. Anda akan melihat bahwa ketika berat berkurang, kurva meluruskan. Agar kurva tidak lari dari grafik, Anda mungkin harus memperbaiki offset.
Akhirnya, tambah bobot ke nilai yang lebih besar dari 100. Kurva akan menjadi lebih curam, dan akhirnya mendekati langkah. Coba sesuaikan offset sehingga sudutnya berada di wilayah titik x = 0,3. Video di bawah ini menunjukkan apa yang harus terjadi:
Kami dapat sangat menyederhanakan analisis kami dengan meningkatkan bobot sehingga output benar-benar merupakan perkiraan yang baik dari fungsi langkah. Di bawah ini saya membuat output neuron tersembunyi atas untuk berat w = 999. Ini adalah gambar statis:
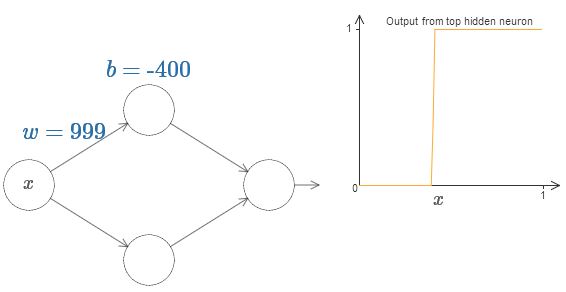
Menggunakan fungsi langkah sedikit lebih mudah daripada dengan sigmoid khas. Alasannya adalah bahwa kontribusi dari semua neuron tersembunyi ditambahkan di lapisan output. Jumlah dari sekelompok fungsi langkah mudah untuk dianalisis, tetapi lebih sulit untuk berbicara tentang apa yang terjadi ketika sekelompok kurva ditambahkan dalam bentuk sigmoid. Oleh karena itu, akan jauh lebih mudah untuk mengasumsikan bahwa neuron tersembunyi kita menghasilkan fungsi bertahap. Lebih tepatnya, kami melakukan ini dengan memperbaiki bobot w pada beberapa nilai yang sangat besar, dan kemudian menetapkan posisi langkah melalui offset. Tentu saja, bekerja dengan output sebagai fungsi langkah adalah perkiraan, tetapi sangat bagus, dan sejauh ini kami akan memperlakukan fungsi tersebut sebagai fungsi langkah yang sebenarnya. Nanti, saya akan kembali untuk membahas efek penyimpangan dari perkiraan ini.
Berapa nilai x adalah langkahnya? Dengan kata lain, bagaimana posisi langkah tergantung pada berat dan perpindahan?
Untuk menjawab pertanyaan, cobalah mengubah bobot dan mengimbangi di bagan interaktif. Bisakah Anda mengerti bagaimana posisi langkah tergantung pada w dan b? Dengan sedikit berlatih, Anda dapat meyakinkan diri sendiri bahwa posisinya proporsional dengan b dan berbanding terbalik dengan w.
Bahkan, langkahnya adalah pada s = โb / w, seperti yang akan terlihat jika kita menyesuaikan berat dan perpindahan ke nilai berikut:
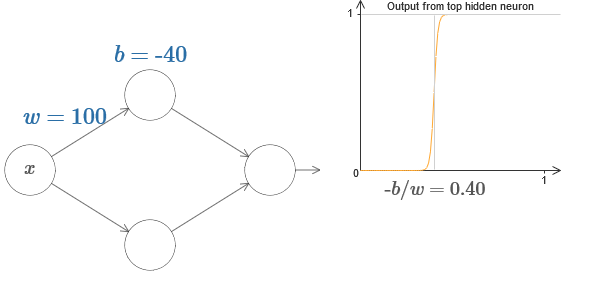
Kehidupan kita akan sangat disederhanakan jika kita menggambarkan neuron tersembunyi dengan parameter tunggal, s, yaitu, dengan posisi langkah, s = โb / w. Dalam diagram interaktif berikut, Anda dapat dengan mudah mengubah s:
Seperti disebutkan di atas, kami secara khusus menetapkan bobot w pada input ke nilai yang sangat besar - cukup besar sehingga fungsi langkah menjadi perkiraan yang baik. Dan kita dapat dengan mudah mengubah neuron yang diparameterisasi dengan cara ini kembali ke bentuk biasanya dengan memilih bias b = โws.
Sejauh ini, kami hanya berkonsentrasi pada output dari neuron tersembunyi superior. Mari kita lihat perilaku seluruh jaringan. Misalkan neuron tersembunyi menghitung fungsi langkah yang didefinisikan oleh parameter langkah s
1 (neuron atas) dan s
2 (neuron bawah). Bobot output masing-masing adalah w
1 dan w
2 . Inilah jaringan kami:
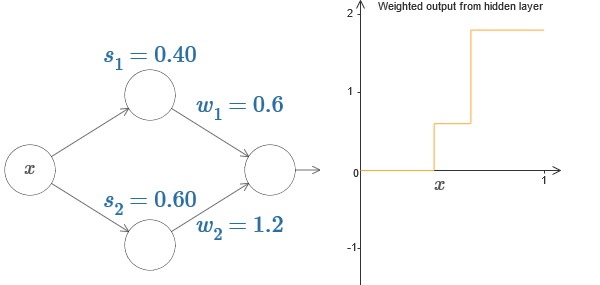
Di sebelah kanan adalah grafik dari output tertimbang w
1 a
1 + w
2 a
2 dari lapisan tersembunyi. Di sini a
1 dan
2 adalah output dari neuron tersembunyi atas dan bawah, masing-masing. Mereka dilambangkan dengan "a", karena mereka sering disebut aktivasi neuron.
By the way, kami mencatat bahwa output dari seluruh jaringan adalah ฯ (w
1 a
1 + w
2 a
2 + b), di mana b adalah bias dari neuron output. Ini, jelas, tidak sama dengan output tertimbang dari lapisan tersembunyi, grafik yang sedang kita bangun. Tetapi untuk saat ini, kami akan berkonsentrasi pada output seimbang dari lapisan tersembunyi, dan hanya kemudian berpikir tentang bagaimana hubungannya dengan output dari seluruh jaringan.
Cobalah untuk menambah dan mengurangi langkah s
1 dari neuron tersembunyi atas pada diagram interaktif
di artikel asli . Lihat bagaimana ini mengubah output tertimbang dari lapisan tersembunyi. Sangat berguna untuk memahami apa yang terjadi ketika s
1 melebihi s
2 . Anda akan melihat bahwa grafik dalam kasus-kasus ini berubah bentuk, ketika kita bergerak dari situasi di mana neuron tersembunyi atas diaktifkan terlebih dahulu ke situasi di mana neuron tersembunyi bawah diaktifkan terlebih dahulu.
Demikian pula, cobalah memanipulasi langkah
2 dari neuron tersembunyi yang lebih rendah dan lihat bagaimana ini mengubah output keseluruhan dari neuron tersembunyi.
Cobalah untuk mengurangi dan meningkatkan bobot keluaran. Perhatikan bagaimana skala ini kontribusi dari neuron tersembunyi yang sesuai. Apa yang terjadi jika salah satu bobot sama dengan 0?
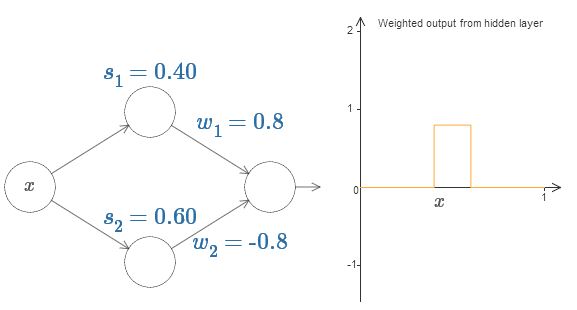
Terakhir, coba atur w
1 ke 0.8 dan w
2 ke -0.8. Hasilnya adalah fungsi "tonjolan", dengan awal pada s
1 , akhir pada s
2 , dan ketinggian 0,8. Misalnya, output tertimbang mungkin terlihat seperti ini:
Tentu saja, tonjolan dapat ditingkatkan ke ketinggian berapa pun. Mari kita gunakan satu parameter, h, yang menunjukkan tinggi. Juga, untuk kesederhanaan, saya akan menghilangkan notasi "s
1 = ..." dan "w
1 = ...".
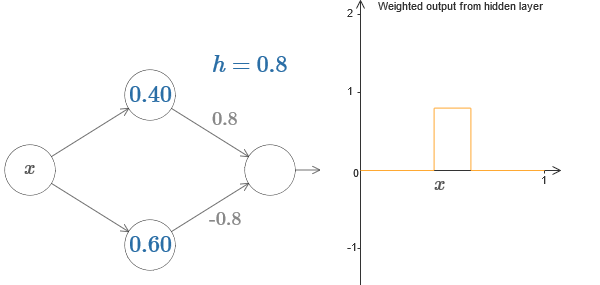
Coba tambah dan kurangi nilai h untuk melihat bagaimana ketinggian penonjolan berubah. Cobalah untuk membuat h negatif. Coba ubah titik langkah untuk mengamati bagaimana ini mengubah bentuk tonjolan.
Anda akan melihat bahwa kami menggunakan neuron kami tidak hanya sebagai grafis primitif, tetapi juga sebagai unit yang lebih akrab bagi programmer - sesuatu seperti instruksi if-then-else dalam pemrograman:
jika input> = mulai dari langkah:
tambahkan 1 ke output tertimbang
lain:
tambahkan 0 ke output tertimbang
Sebagian besar saya akan menempel pada notasi grafis. Namun, kadang-kadang akan berguna bagi Anda untuk beralih ke tampilan if-then-else dan merenungkan apa yang terjadi dalam istilah-istilah ini.
Kita dapat menggunakan trik penonjolan kita dengan menempelkan dua bagian neuron tersembunyi bersama di jaringan yang sama:
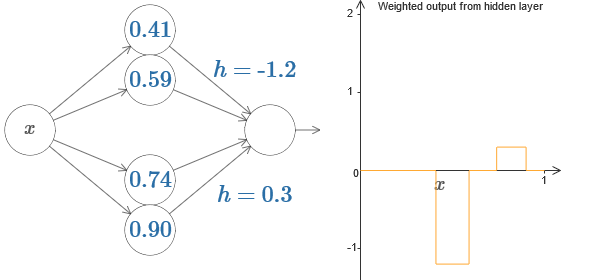
Di sini saya menjatuhkan bobot dengan hanya menuliskan nilai h untuk setiap pasangan neuron tersembunyi. Coba mainkan dengan kedua nilai h dan lihat bagaimana ia mengubah grafik. Pindahkan tab, ubah titik langkah.
Dalam kasus yang lebih umum, ide ini dapat digunakan untuk mendapatkan jumlah puncak yang diinginkan dari ketinggian berapa pun. Secara khusus, kita dapat membagi interval [0,1] menjadi sejumlah besar subintervals (N), dan menggunakan pasangan N neuron tersembunyi untuk mendapatkan puncak dari ketinggian yang diinginkan. Mari kita lihat bagaimana ini bekerja untuk N = 5. Ini sudah cukup banyak neuron, jadi saya presentasi sedikit lebih sempit. Maaf untuk diagram yang rumit - Saya bisa menyembunyikan kerumitan di balik abstraksi tambahan, tetapi bagi saya nilainya sedikit siksaan dengan kerumitan agar lebih merasakan bagaimana kerja jaringan saraf.
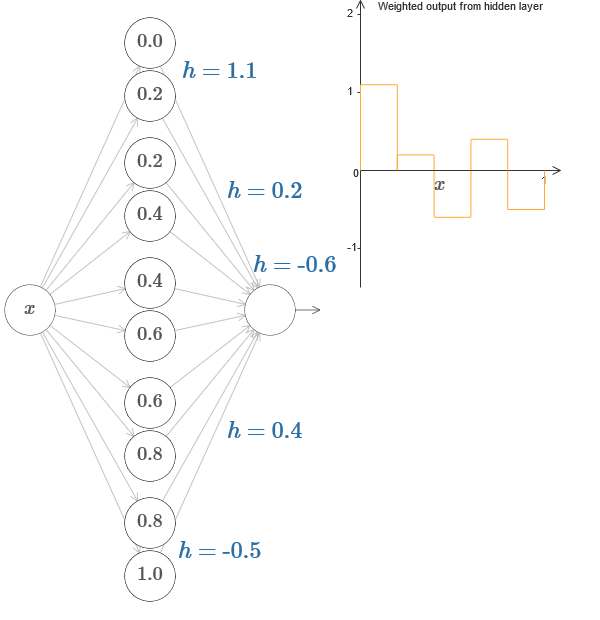
Anda tahu, kami memiliki lima pasang neuron tersembunyi. Poin dari langkah-langkah pasangan yang sesuai terletak di 0,1 / 5, lalu 1 / 5,2 / 5, dan seterusnya, hingga 4 / 5,5 / 5. Nilai-nilai ini adalah tetap - kami mendapatkan lima tonjolan dengan lebar yang sama pada grafik.
Setiap pasangan neuron memiliki nilai h yang terkait dengannya. Ingat bahwa koneksi neuron output memiliki bobot h dan โh. Dalam artikel asli pada bagan, Anda dapat mengklik nilai h dan memindahkannya ke kiri-kanan. Dengan perubahan ketinggian, jadwal juga berubah. Dengan mengubah bobot keluaran, kami membangun fungsi akhir!
Pada diagram, Anda masih dapat mengklik grafik, dan seret ketinggian langkah ke atas atau ke bawah. Ketika Anda mengubah ketinggiannya, Anda akan melihat bagaimana ketinggian h yang terkait berubah. Output bobot + h dan โh berubah sesuai. Dengan kata lain, kami secara langsung memanipulasi fungsi yang grafiknya diperlihatkan di sebelah kanan dan melihat perubahan ini dalam nilai h di sebelah kiri. Anda juga dapat menahan tombol mouse di salah satu tonjolan, lalu seret mouse ke kiri atau kanan, dan tonjolan akan menyesuaikan dengan ketinggian saat ini.
Saatnya menyelesaikan pekerjaan.
Ingat fungsi yang saya gambar di awal bab ini:
Lalu saya tidak menyebutkan ini, tetapi sebenarnya ini terlihat seperti ini:
Ini dibangun untuk nilai x dari 0 hingga 1, dan nilai sepanjang sumbu y bervariasi dari 0 hingga 1.
Jelas, fungsi ini tidak trivial. Dan Anda harus mencari cara menghitungnya menggunakan jaringan saraf.
Dalam jaringan saraf kami di atas, kami menganalisis kombinasi berbobot โjwj dari output neuron tersembunyi. Kami tahu cara mendapatkan kontrol yang signifikan atas nilai ini. Tetapi, seperti yang saya sebutkan sebelumnya, nilai ini tidak sama dengan output jaringan. Output dari jaringan adalah ฯ (โ
jw j a
j + b), di mana b adalah perpindahan dari neuron output. Bisakah kita mendapatkan kontrol langsung atas output jaringan?
Solusinya adalah mengembangkan jaringan saraf di mana output tertimbang dari lapisan tersembunyi diberikan oleh persamaan ฯ
โ1 โ
f (x), di mana ฯ
โ1 adalah fungsi kebalikan dari ฯ. Artinya, kami ingin output tertimbang dari lapisan tersembunyi menjadi seperti ini:
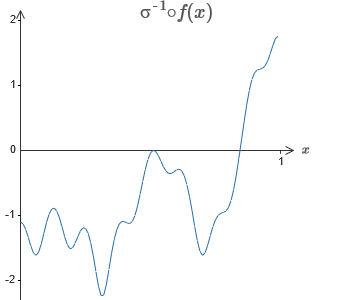Jika ini berhasil, maka output dari seluruh jaringan akan menjadi perkiraan yang baik untuk f (x) (saya mengatur offset neuron output ke 0).Maka tugas Anda adalah mengembangkan NS yang mendekati fungsi objektif yang ditunjukkan di atas. Untuk lebih memahami apa yang terjadi, saya sarankan Anda menyelesaikan masalah ini dua kali. Untuk pertama kalinya dalam artikel asli, klik pada grafik, dan langsung sesuaikan ketinggian dari berbagai tonjolan. Ini akan sangat mudah bagi Anda untuk mendapatkan perkiraan yang baik untuk fungsi tujuan. Tingkat perkiraan diperkirakan oleh deviasi rata-rata, perbedaan antara fungsi tujuan dan fungsi yang dihitung jaringan. Tugas Anda adalah membawa deviasi rata-rata ke nilai minimum. Tugas dianggap selesai ketika simpangan rata-rata tidak melebihi 0.40.
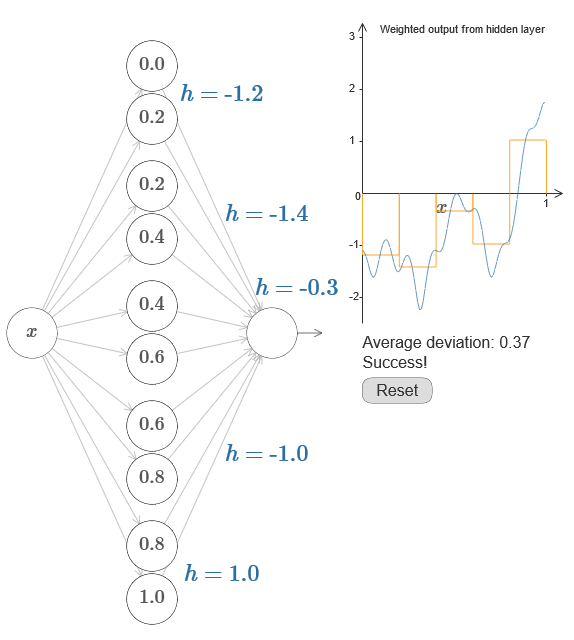Setelah mencapai kesuksesan, tekan tombolReset, yang mengubah tab secara acak. Kedua kalinya, jangan menyentuh grafik, tetapi ubah nilai h di sisi kiri diagram, mencoba membawa deviasi rata-rata ke nilai 0,40 atau kurang.Jadi, Anda telah menemukan semua elemen yang diperlukan jaringan untuk menghitung fungsi f (x)! Perkiraannya ternyata kasar, tetapi kita dapat dengan mudah meningkatkan hasilnya dengan hanya meningkatkan jumlah pasangan neuron tersembunyi, yang akan meningkatkan jumlah tonjolan.Secara khusus, mudah untuk mengubah semua data yang ditemukan kembali ke tampilan standar dengan parameterisasi yang digunakan untuk NS. Biarkan saya dengan cepat mengingatkan Anda bagaimana ini bekerja.Pada lapisan pertama, semua bobot memiliki nilai konstanta yang besar, misalnya, w = 1000.Perpindahan neuron tersembunyi dihitung melalui b = โws. Jadi, misalnya, untuk neuron tersembunyi kedua, s = 0,2 berubah menjadi b = 0001000 ร 0,2 = โ200.Lapisan terakhir dari skala ditentukan oleh nilai-nilai h. Jadi, misalnya, nilai yang Anda pilih untuk h pertama, h = -0.2, berarti bahwa bobot keluaran dari dua neuron tersembunyi atas masing-masing adalah -0,2 dan 0,2. Dan seterusnya, untuk seluruh lapisan bobot keluaran.Akhirnya, offset neuron output adalah 0.Dan hanya itu: kami mendapat deskripsi lengkap NS, yang menghitung fungsi tujuan awal dengan baik. Dan kami memahami bagaimana meningkatkan kualitas perkiraan dengan meningkatkan jumlah neuron tersembunyi.Selain itu, dalam fungsi tujuan awal kami f (x) = 0,2 + 0,4x 2+ 0.3sin (15x) + 0.05cos (50x) tidak ada yang istimewa. Prosedur serupa dapat digunakan untuk fungsi kontinu pada interval dari [0,1] ke [0,1]. Bahkan, kami menggunakan NS single-layer kami untuk membangun tabel pencarian untuk suatu fungsi. Dan kita dapat mengambil ide ini sebagai dasar untuk mendapatkan bukti universalitas yang menyeluruh.Fungsi banyak parameter
Kami memperluas hasil kami ke kasus satu set variabel input. Kedengarannya rumit, tetapi semua ide yang kita butuhkan sudah dapat dipahami untuk kasus ini dengan hanya dua variabel yang masuk. Oleh karena itu, kami mempertimbangkan kasus dengan dua variabel yang masuk.Mari kita mulai dengan melihat apa yang terjadi ketika neuron memiliki dua input: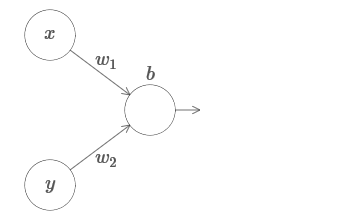
Kami memiliki input x dan y, dengan bobot yang sesuai w 1 dan w 2 dan mengimbangi b dari neuron. Kami mengatur bobot w 2 hingga 0 dan bermain dengan yang pertama, w 1 , dan mengimbangi b untuk melihat bagaimana mereka memengaruhi output neuron:
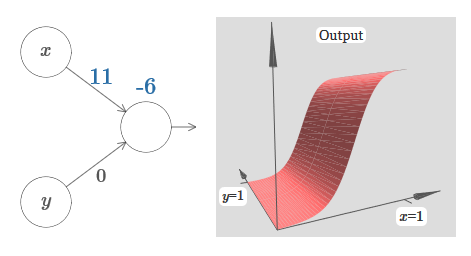Seperti yang Anda lihat, dengan w 2 = 0, input y tidak memengaruhi output neuron. Semuanya terjadi seolah-olah x adalah satu-satunya input.Dengan ini, menurut Anda apa yang akan terjadi ketika kami menambah bobot w 1 ke w 1 = 100 dan w 2 meninggalkan 0? Jika ini tidak segera jelas bagi Anda, pikirkan sedikit tentang masalah ini. Kemudian tonton video berikut, yang menunjukkan apa yang akan terjadi:
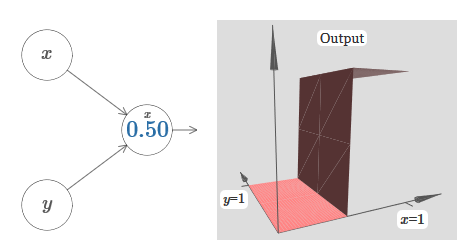Kami menganggap bahwa bobot input x sangat penting - Saya menggunakan w 1 = 1000 - dan bobot w 2 = 0. Angka pada neuron adalah posisi langkah, dan x di atasnya mengingatkan kita bahwa kita memindahkan langkah di sepanjang sumbu x. Secara alami, sangat mungkin untuk mendapatkan fungsi langkah di sepanjang sumbu y, membuat bobot masuk untuk y besar (misalnya, w 2= 1000), dan bobot untuk x adalah 0, w 1 = 0:
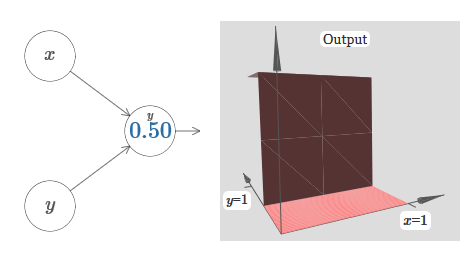Angka pada neuron, sekali lagi, menunjukkan posisi langkah, dan y di atasnya mengingatkan kita bahwa kita memindahkan langkah di sepanjang sumbu y. Saya bisa langsung menunjuk bobot untuk x dan y, tetapi saya tidak melakukannya, karena itu akan mengotori bagan. Tetapi perlu diingat bahwa penanda y menunjukkan bahwa berat untuk y adalah besar dan untuk x adalah 0.Kita dapat menggunakan fungsi langkah yang baru saja kita rancang untuk menghitung fungsi penonjolan tiga dimensi. Untuk melakukan ini, kita mengambil dua neuron, yang masing-masing akan menghitung fungsi langkah di sepanjang sumbu x. Kemudian kita menggabungkan fungsi langkah ini dengan bobot h dan โh, di mana h adalah tinggi penonjolan yang diinginkan. Semua ini dapat dilihat pada diagram berikut:
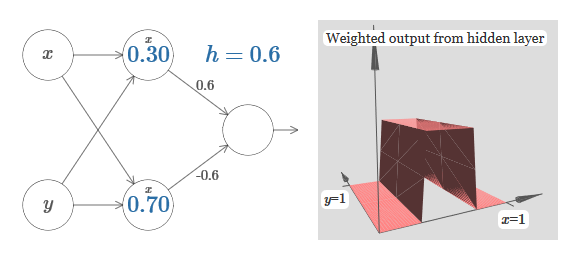Coba ubah nilai h. Lihat bagaimana kaitannya dengan bobot jaringan. Dan bagaimana dia mengubah ketinggian fungsi tonjolan di sebelah kanan.Coba juga untuk mengubah titik langkah, nilai yang diatur ke 0,30 di neuron tersembunyi atas. Lihat bagaimana itu mengubah bentuk tonjolan. Apa yang terjadi jika Anda memindahkannya melampaui titik 0,70 yang terkait dengan neuron tersembunyi yang lebih rendah?Kami belajar bagaimana membangun fungsi tonjolan di sepanjang sumbu x. Secara alami, kita dapat dengan mudah membuat fungsi tonjolan di sepanjang sumbu y, menggunakan dua fungsi langkah di sepanjang sumbu y. Ingatlah bahwa kita dapat melakukan ini dengan membuat bobot besar pada input y, dan mengatur bobot 0 pada input x. Jadi, apa yang terjadi:
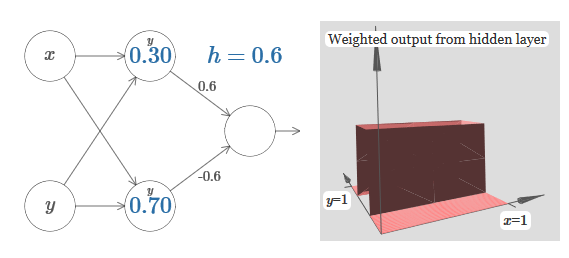Itu terlihat hampir identik dengan jaringan sebelumnya! Satu-satunya perubahan yang terlihat adalah penanda y kecil pada neuron tersembunyi. Mereka mengingatkan kita bahwa mereka menghasilkan fungsi langkah untuk y, dan bukan untuk x, sehingga bobot pada input y sangat besar, dan pada input x itu adalah nol, dan bukan sebaliknya. Seperti sebelumnya, saya memutuskan untuk tidak menampilkannya secara langsung, agar tidak mengacaukan gambar.Mari kita lihat apa yang terjadi jika kita menambahkan dua fungsi tonjolan, satu di sepanjang sumbu x, yang lain di sepanjang sumbu y, keduanya tingginya h:
Untuk menyederhanakan diagram koneksi dengan bobot nol, saya hilangkan. Sejauh ini, saya telah meninggalkan penanda x dan y kecil pada neuron tersembunyi untuk mengingat ke arah mana fungsi tonjolan dihitung. Nanti kita akan menolak mereka, karena mereka tersirat oleh variabel yang masuk.Coba ubah parameter h. Seperti yang Anda lihat, karena ini, bobot output berubah, serta bobot dari kedua fungsi penonjolan, x dan y.Apa yang kami buat sedikit mirip dengan "fungsi menara":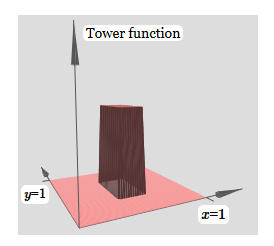
Jika kami dapat membuat fungsi menara seperti itu, kami dapat menggunakannya untuk memperkirakan fungsi sewenang-wenang dengan hanya menambahkan menara berbagai ketinggian di tempat yang berbeda:
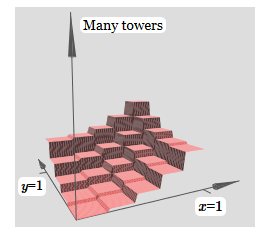Tentu saja, kami belum mencapai pembuatan fungsi menara yang sewenang-wenang. Sejauh ini, kami telah membangun sesuatu seperti menara pusat tinggi 2 jam dengan dataran tinggi h di sekitarnya.Tapi kita bisa membuat fungsi menara. Ingatlah bahwa kami sebelumnya menunjukkan bagaimana neuron dapat digunakan untuk mengimplementasikan pernyataan if-then-else:if >= : 1 else: 0
Itu adalah neuron satu input. Dan kita perlu menerapkan ide yang mirip dengan output gabungan dari neuron tersembunyi:
if >= : 1 else: 0
Jika kita memilih ambang kanan - misalnya, 3 jam / 2, terjepit di antara ketinggian dataran tinggi dan ketinggian menara pusat - kita dapat menghancurkan dataran tinggi itu hingga nol, dan hanya menyisakan satu menara.
Bayangkan bagaimana melakukan ini? Coba bereksperimen dengan jaringan berikut. Sekarang kita sedang merencanakan keluaran dari seluruh jaringan, dan bukan hanya keluaran tertimbang dari lapisan tersembunyi. Ini berarti bahwa kami menambahkan istilah offset ke output tertimbang dari lapisan tersembunyi, dan menerapkan sigmoid tersebut. Bisakah Anda menemukan nilai untuk h dan b yang Anda dapatkan menara? Jika Anda terjebak pada titik ini, berikut adalah dua tips: (1) agar neuron yang keluar menunjukkan perilaku if-then-else, kita perlu bobot yang masuk (semua jam atau โj) menjadi besar; (2) nilai b menentukan skala ambang if-then-else.
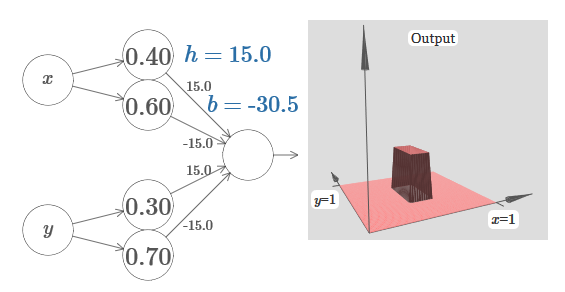
Dengan parameter default, output mirip dengan versi rata dari diagram sebelumnya, dengan menara dan dataran tinggi. Untuk mendapatkan perilaku yang diinginkan, Anda perlu meningkatkan nilai h. Ini akan memberi kita perilaku ambang jika-maka-lain. Kedua, untuk mengatur ambang dengan benar, seseorang harus memilih b โ โ3h / 2.
Begini tampilannya untuk h = 10:
Bahkan untuk nilai h yang relatif sederhana, kami mendapatkan fungsi menara yang bagus. Dan, tentu saja, kita bisa mendapatkan hasil yang indah secara sewenang-wenang dengan meningkatkan h lebih jauh dan menjaga bias pada tingkat b = h3j / 2.
Mari kita coba merekatkan dua jaringan bersama untuk menghitung dua fungsi menara yang berbeda. Untuk memperjelas peran masing-masing dari dua subnet, saya menempatkannya dalam persegi panjang yang terpisah: masing-masing menghitung fungsi menara menggunakan teknik yang dijelaskan di atas. Grafik di sebelah kanan menunjukkan keluaran tertimbang dari lapisan tersembunyi kedua, yaitu, kombinasi tertimbang dari fungsi menara.
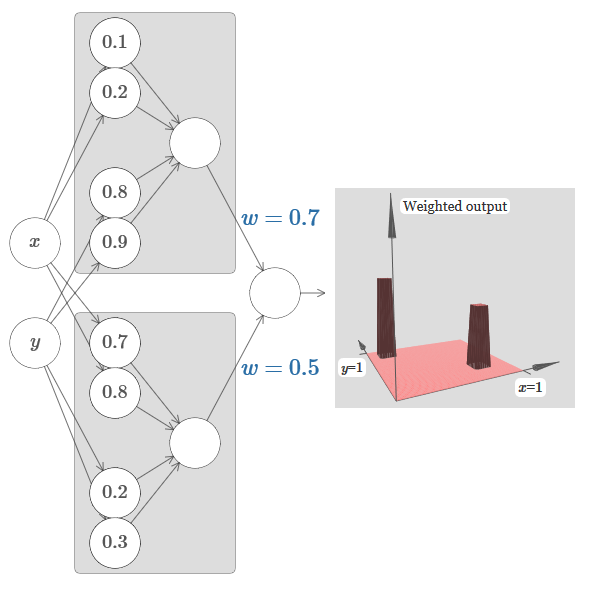
Secara khusus, dapat dilihat bahwa dengan mengubah bobot pada lapisan terakhir, Anda dapat mengubah ketinggian menara keluaran.
Gagasan yang sama memungkinkan Anda menghitung menara sebanyak yang Anda suka. Kita bisa membuat mereka semena-mena tipis dan tinggi. Sebagai hasilnya, kami menjamin bahwa keluaran tertimbang dari lapisan tersembunyi kedua mendekati fungsi apa pun yang diinginkan dari dua variabel:
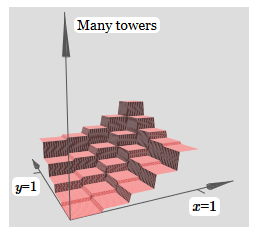
Secara khusus, dengan membuat output tertimbang dari lapisan tersembunyi kedua mendekati ฯ
โ1 โ
f dengan baik, kami menjamin bahwa output jaringan kami akan menjadi perkiraan yang baik dari fungsi yang diinginkan f.
Bagaimana dengan fungsi banyak variabel?
Mari kita coba mengambil tiga variabel, x
1 , x
2 , x
3 . Dapatkah jaringan berikut digunakan untuk menghitung fungsi menara dalam empat dimensi?
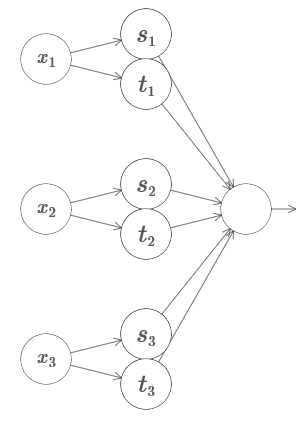
Di sini x
1 , x
2 , x
3 menunjukkan input jaringan. s
1 , t
1, dan seterusnya - titik langkah untuk neuron - yaitu, semua bobot pada lapisan pertama besar, dan offset ditetapkan sehingga titik langkah adalah s
1 , t
1 , s
2 , ... Bobot pada lapisan kedua berganti, + h, โh, di mana h adalah angka yang sangat besar. Output offset adalah โ5j / 2.
Jaringan menghitung fungsi sama dengan 1 dalam tiga kondisi: x
1 adalah antara s
1 dan t
1 ; x
2 adalah antara s
2 dan t
2 ; x
3 berada di antara s
3 dan t
3 . Jaringan adalah 0 di semua tempat lain. Ini adalah menara di mana 1 adalah bagian kecil dari ruang masuk, dan 0 adalah segalanya.
Merekatkan banyak jaringan seperti itu, kita bisa mendapatkan menara sebanyak yang kita suka, dan memperkirakan fungsi sewenang-wenang dari tiga variabel. Gagasan yang sama bekerja dalam dimensi m. Hanya offset keluaran (+m + 1/2) h yang diubah untuk menekan dengan benar nilai yang diinginkan dan menghapus dataran tinggi.
Nah, sekarang kita tahu cara menggunakan NS untuk memperkirakan fungsi sebenarnya dari banyak variabel. Bagaimana dengan fungsi vektor f (x
1 , ..., x
m ) โ R
n ? Tentu saja, fungsi seperti itu dapat dianggap hanya sebagai n fungsi nyata yang terpisah f1 (x
1 , ..., x
m ), f2 (x
1 , ..., x
m ), dan seterusnya. Dan kemudian kita hanya merekatkan semua jaringan bersama. Jadi mudah untuk mengetahuinya.
Tantangan
- Kami melihat bagaimana menggunakan jaringan saraf dengan dua lapisan tersembunyi untuk memperkirakan fungsi sewenang-wenang. Bisakah Anda membuktikan bahwa ini mungkin dengan satu lapisan tersembunyi? Petunjuk - coba bekerja dengan hanya dua variabel keluaran, dan tunjukkan bahwa: (a) dimungkinkan untuk mendapatkan fungsi langkah-langkah tidak hanya sepanjang sumbu x atau y, tetapi juga dalam arah sewenang-wenang; (b) menjumlahkan banyak konstruksi dari langkah (a), adalah mungkin untuk memperkirakan fungsi putaran daripada menara persegi panjang; ยฉ menggunakan menara bundar, dimungkinkan untuk memperkirakan fungsi yang berubah-ubah. Langkah ยฉ akan lebih mudah dilakukan dengan menggunakan materi yang disajikan dalam bab ini sedikit di bawah.
Melampaui neuron sigmoid
Kami telah membuktikan bahwa jaringan neuron sigmoid dapat menghitung fungsi apa pun. Ingat bahwa dalam neuron sigmoid, input x
1 , x
2 , ... berubah pada output menjadi ฯ (jw
j x
j j + b), di mana w
j adalah bobot, b adalah bias, dan ฯ adalah sigmoid.
Bagaimana jika kita melihat tipe neuron lain menggunakan fungsi aktivasi yang berbeda, s (z):
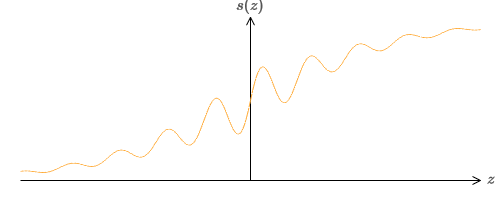
Yaitu, kita mengasumsikan bahwa jika sebuah neuron memiliki x
1 , x
2 , ... bobot w
1 , w
2 , ... dan bias b, maka s (jw
j x
j + b) akan menjadi output.
Kita dapat menggunakan fungsi aktivasi ini untuk melangkah, seperti dalam kasus sigmoid. Coba (dalam
artikel asli ) pada diagram untuk mengangkat beban, katakanlah, w = 100:
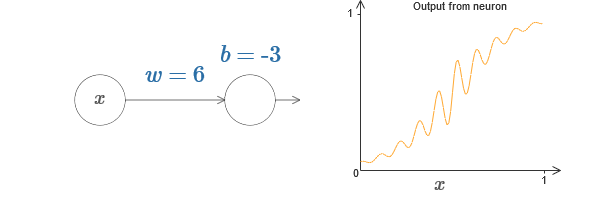
Seperti dalam kasus sigmoid, karena ini, fungsi aktivasi dikompresi, dan sebagai hasilnya berubah menjadi perkiraan yang sangat baik dari fungsi langkah. Coba ubah offset, dan Anda akan melihat bahwa kami dapat mengubah lokasi langkah menjadi apa pun. Karena itu, kita dapat menggunakan semua trik yang sama seperti sebelumnya untuk menghitung fungsi yang diinginkan.
Properti apa yang harus dimiliki s (z) agar ini berfungsi? Kita perlu berasumsi bahwa s (z) didefinisikan dengan baik sebagai z โ โโ dan z โ โ. Batasan ini adalah dua nilai yang diterima oleh fungsi langkah kami. Kita juga perlu mengasumsikan bahwa batasan ini berbeda. Jika mereka tidak berbeda, langkah-langkahnya tidak akan berhasil, hanya akan ada jadwal yang datar! Tetapi jika fungsi aktivasi s (z) memenuhi sifat-sifat ini, neuron yang didasarkan padanya secara universal cocok untuk perhitungan.
Tugasnya
- Sebelumnya dalam buku ini, kami bertemu dengan jenis neuron yang berbeda - neuron linear yang diluruskan, atau unit linear yang diperbaiki, ReLU. Jelaskan mengapa neuron semacam itu tidak memenuhi kondisi yang diperlukan untuk universalitas. Temukan bukti keserbagunaan yang menunjukkan bahwa ReLU secara universal cocok untuk komputasi.
- Misalkan kita sedang mempertimbangkan neuron linier, dengan fungsi aktivasi s (z) = z. Jelaskan mengapa neuron linier tidak memenuhi kondisi universalitas. Tunjukkan bahwa neuron semacam itu tidak dapat digunakan untuk komputasi universal.
Perbaiki fungsi langkah
Untuk saat ini, kami mengasumsikan bahwa neuron kami menghasilkan fungsi langkah yang akurat. Ini adalah perkiraan yang baik, tetapi hanya perkiraan. Bahkan, ada celah kegagalan yang sempit, yang ditunjukkan pada grafik berikut, di mana fungsi-fungsinya tidak berperilaku sama sekali seperti fungsi langkah:
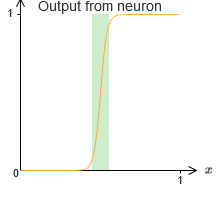
Dalam periode kegagalan ini, penjelasan saya tentang universalitas tidak berfungsi.
Kegagalan tidak begitu menakutkan. Dengan mengatur bobot input yang cukup besar, kita dapat membuat kesenjangan ini kecil secara sewenang-wenang. Kita bisa membuatnya lebih kecil dari pada grafik, tidak terlihat oleh mata. Jadi mungkin kita tidak perlu khawatir tentang masalah ini.
Namun demikian, saya ingin memiliki beberapa cara untuk menyelesaikannya.
Ternyata itu mudah dipecahkan. Mari kita lihat solusi ini untuk menghitung fungsi NS dengan hanya satu input dan output. Gagasan yang sama akan bekerja untuk menyelesaikan masalah dengan sejumlah besar input dan output.
Secara khusus, misalkan kita ingin jaringan kita menghitung beberapa fungsi f. Seperti sebelumnya, kami mencoba melakukan ini dengan mendesain jaringan sehingga keluaran tertimbang dari lapisan neuron yang tersembunyi adalah ฯ
โ1 โ
f (x):
Jika kita melakukan ini menggunakan teknik yang dijelaskan di atas, kita akan memaksa neuron yang tersembunyi untuk menghasilkan urutan fungsi tonjolan:
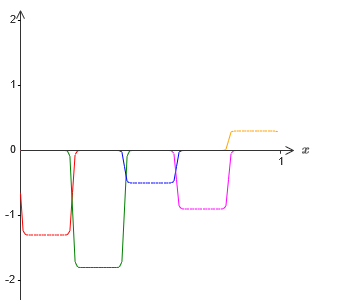
Tentu saja, saya melebih-lebihkan ukuran interval kegagalan, sehingga lebih mudah dilihat. Harus jelas bahwa jika kita menjumlahkan semua fungsi tonjolan ini, kita mendapatkan perkiraan yang cukup baik dari ฯ
โ1 โ
f (x) di mana-mana kecuali untuk interval kegagalan.
Tetapi anggaplah bahwa alih-alih menggunakan perkiraan yang baru saja dijelaskan, kita menggunakan satu set neuron tersembunyi untuk menghitung perkiraan setengah dari fungsi tujuan awal kita, yaitu, ฯ
โ1 โ
f (x) / 2. Tentu saja, itu akan terlihat seperti versi skala dari grafik terbaru:
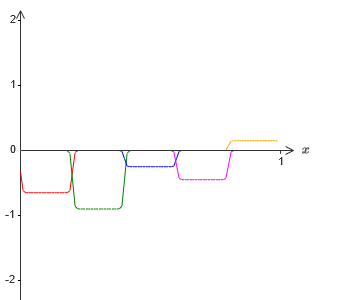
Dan anggaplah kita membuat satu set neuron tersembunyi menghitung perkiraan untuk ฯ
โ1 โ
f (x) / 2, namun, pada dasarnya tonjolan akan digeser setengah lebar:
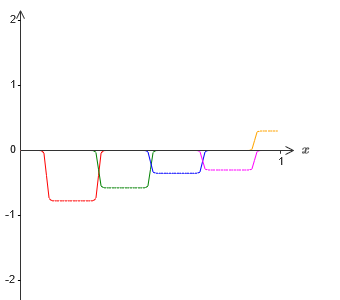
Sekarang kita memiliki dua perkiraan berbeda untuk ฯ - 1โ
f (x) / 2. Jika kita menjumlahkan dua perkiraan ini, kita memperoleh perkiraan umum untuk ฯ - 1โ
f (x). Perkiraan umum ini masih akan memiliki ketidakakuratan dalam interval kecil. Tetapi masalahnya akan lebih kecil dari sebelumnya - karena titik-titik yang jatuh ke dalam interval kegagalan dari aproksimasi pertama tidak akan jatuh ke dalam interval kegagalan aproksimasi kedua. Oleh karena itu, perkiraan dalam interval ini akan menjadi sekitar 2 kali lebih baik.
Kita dapat memperbaiki situasi dengan menambahkan sejumlah besar, M, dari tumpang tindih perkiraan fungsi ฯ - 1โ
f (x) / M. Jika semua interval kegagalannya cukup sempit, arus apa pun hanya ada di salah satunya. Jika Anda menggunakan cukup banyak perkiraan M yang tumpang tindih, hasilnya adalah perkiraan umum yang sangat baik.
Kesimpulan
Penjelasan tentang universalitas yang dibahas di sini pasti tidak bisa disebut deskripsi praktis tentang bagaimana cara menghitung fungsi menggunakan jaringan saraf! Dalam hal ini, ini lebih seperti bukti fleksibilitas gerbang logika NAND dan banyak lagi. Oleh karena itu, saya pada dasarnya mencoba membuat desain ini jelas dan mudah diikuti tanpa mengoptimalkan detailnya. Namun, mencoba mengoptimalkan desain ini bisa menjadi latihan yang menarik dan instruktif untuk Anda.
Meskipun hasil yang diperoleh tidak dapat langsung digunakan untuk membuat NS, ini penting karena menghilangkan pertanyaan tentang komputabilitas fungsi tertentu menggunakan NS. Jawaban untuk pertanyaan seperti itu akan selalu positif. Oleh karena itu, sudah benar untuk menanyakan apakah ada fungsi yang dapat dihitung, tetapi apa cara yang benar untuk menghitungnya.
Desain universal kami hanya menggunakan dua lapisan tersembunyi untuk menghitung fungsi arbitrer. Seperti yang telah kita diskusikan, adalah mungkin untuk mendapatkan hasil yang sama dengan satu lapisan tersembunyi. Dengan ini, Anda mungkin bertanya-tanya mengapa kami membutuhkan jaringan yang dalam, yaitu jaringan dengan sejumlah besar lapisan tersembunyi. Tidak bisakah kita hanya mengganti jaringan ini dengan yang dangkal yang memiliki satu lapisan tersembunyi?
Meskipun pada prinsipnya dimungkinkan, ada alasan praktis yang baik untuk menggunakan jaringan saraf yang dalam. Seperti dijelaskan dalam Bab 1, NS mendalam memiliki struktur hierarkis yang memungkinkan mereka beradaptasi dengan baik untuk mempelajari pengetahuan hierarkis, yang berguna untuk memecahkan masalah nyata. Lebih khusus lagi, ketika memecahkan masalah seperti pengenalan pola, akan berguna untuk menggunakan sistem yang tidak hanya memahami piksel individu, tetapi juga konsep yang semakin kompleks: dari batas ke bentuk geometris sederhana, dan seterusnya, ke adegan kompleks yang melibatkan beberapa objek. Dalam bab-bab selanjutnya kita akan melihat bukti yang mendukung fakta bahwa NS mendalam akan lebih mampu mengatasi studi hierarki pengetahuan seperti itu daripada yang dangkal. Ringkasnya: universalitas memberi tahu kita bahwa NS dapat menghitung fungsi apa pun; bukti empiris menunjukkan bahwa NS mendalam lebih baik disesuaikan dengan studi fungsi yang berguna untuk memecahkan banyak masalah dunia nyata.