Metode Analisis Cluster Baru

Metode baru analisis cluster diusulkan. Keuntungannya adalah dalam algoritma komputasi yang kurang kompleks. Metode ini didasarkan pada perhitungan suara untuk fakta bahwa sepasang objek berada di kelas yang sama dari informasi tentang nilai koordinat individu.

Pendahuluan

Kebutuhan besar untuk analisis data adalah pengembangan metode klasifikasi yang efektif. Dalam metode tersebut, diperlukan untuk membagi seluruh rangkaian objek ke dalam jumlah kelas yang optimal, hanya berdasarkan informasi tentang nilai indikator individu [Zagoruyko 1999].

Analisis cluster adalah salah satu metode analisis data dan statistik matematika yang paling populer. Analisis Cluster memungkinkan Anda untuk secara otomatis menemukan kelas objek, hanya menggunakan informasi tentang indikator kuantitatif objek (pelatihan tanpa guru). Setiap kelas seperti itu dapat didefinisikan oleh salah satu objek yang paling khas, misalnya, rata-rata dalam hal indikator. Ada sejumlah besar metode dan pendekatan untuk mengklasifikasikan data.

Penelitian modern di bidang analisis cluster dilakukan untuk meningkatkan metode untuk menentukan kelas topologi kompleks [Furaoa 2007, Zagoruiko 2013], serta untuk meningkatkan kecepatan algoritma dalam kasus big data.

Dalam tulisan ini, kami mengusulkan metode klasifikasi berdasarkan perolehan suara untuk sepasang objek di kelas yang sama, berdasarkan informasi tentang nilai indikator individu. Diusulkan untuk mempertimbangkan bahwa sepasang objek berada dalam kelas yang sama jika nilai indikator masing-masing berada dalam interval dengan panjang tidak melebihi nilai yang diberikan.

Metode K-means

Metode k-means adalah salah satu metode pengelompokan yang paling populer. Tujuannya adalah untuk mendapatkan pusat data tersebut yang akan sesuai dengan hipotesis kekompakan kelas data dengan distribusi radial simetris mereka. Salah satu cara untuk menentukan posisi pusat-pusat tersebut, mengingat nomornya \ textit {k}, adalah pendekatan EM.

Dalam metode ini, dua prosedur dilakukan secara berurutan.

1. Definisi untuk setiap objek data$$ $ inline $ X_ {i} $ inline $ pusat terdekat$$ $ inline $ C_ {j} $ inline $ , dan menetapkan label kelas untuk objek ini$$ $ inline $ X_ {i} ^ {j} $ inline $ . Selanjutnya, untuk semua objek, milik mereka dari kelas yang berbeda menjadi ditentukan.
2. Perhitungan posisi baru pusat dari semua kelas.

Mengulangi secara berulang kedua prosedur ini dari posisi acak awal pusat-pusat kelas \ textit {k}, kita dapat mencapai pemisahan objek menjadi kelas-kelas yang paling sesuai dengan hipotesis kekompakan radial kelas.

Algoritma klasifikasi penulis baru akan dibandingkan dengan metode k-means.

Metode baru

Algoritme analisis kluster baru dibangun berdasarkan suara untuk kelompok yang berbeda dari informasi tentang nilai-nilai koordinat individu dari titik data.

1. Nilai d ditentukan yang mencirikan panjang interval indikator di mana dua objek dianggap milik kelas yang sama.
2. Metrik yang dipilih$$ $ inline $ x_ {i} $ inline $ dan semua pasangan benda dipertimbangkan$$ $ inline $ \ left \ {O_ {l}, O_ {k} \ right \} $ inline $ dimana$$ $ inline $ l, k = 1 \ ldots N $ inline $ .
3. Jika$$ $ inline $ \ left | x_ {i} ^ {l} -x_ {i} ^ {k} \ kanan | \ le d $ inline $ maka besarnya$$ $ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (suara ditambahkan).
4. Tindakan 2) dan 3) diulang untuk semua indikator$$ $ inline $ i = 1 \ ldots M $ inline $ .
5. Nilai p yang mencirikan jumlah minimum suara untuk memiliki kelas yang sama ditetapkan.
6. Menggunakan metode kunci pasangan nilai, semua kelas objek ditentukan, sedemikian sehingga dalam satu kelas suara untuk pasangan objek dari kelas ini > = p .
7. Iterasi semua nilai d dan p dan ulangi item 1) - 6) untuk mendapatkan jumlah kelas yang paling dekat dengan jumlah kelas yang diberikan g .

Untuk mengurangi kompleksitas algoritme menjadi N , Anda dapat menggunakan interval T untuk indikator individual dan mengganti klausa 2) dan 3) dalam algoritme dengan yang berikut:

1. Indikator dipilih$$ $ inline $ x_ {i} $ inline $ dan semua interval dipertimbangkan$$ $ inline $ \ left [u_ {l}, w_ {l} \ right] $ inline $ dimana$$ $ inline $ l = 1 \ ldots T $ inline $ :

$$$$ menampilkan $$ u_ {0} = \ min (x_ {i}); u_ {0} = \ min (x_ {i}); $$ menampilkan $$

$$$$ menampilkan $$ w_ {T} = \ maks (x_ {i}); $$ menampilkan $$

$$$$ menampilkan $$ s_ {i} = w_ {T} -u_ {0}; $$ menampilkan $$

$$$$ menampilkan $$ u_ {l} = u_ {0} + l \ cdot s_ {i}; $$ menampilkan $$

$$$$ menampilkan $$ w_ {l} = u_ {l} + d; $$ menampilkan $$

2. Jika$$ $ inline $ x_ {i} ^ {k} \ di \ kiri [u_ {j}, w_ {j} \ kanan] $ inline $ dan$$ $ sebaris $ x_ {i} ^ {l} \ di \ kiri [u_ {j}, w_ {j} \ kanan] $ sebaris $ dimana$$ $ inline $ j = 1 \ ldots T $ inline $ maka besarnya$$ $ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (suara ditambahkan dengan tombol unik l , k untuk indikator ke- i ).

Eksperimen numerik

Data dengan klasifikasi intuitif untuk manusia diambil sebagai data awal.

Gambar 1 dan 2 menunjukkan hasil klasifikasi metode k-means dan metode klasifikasi baru.


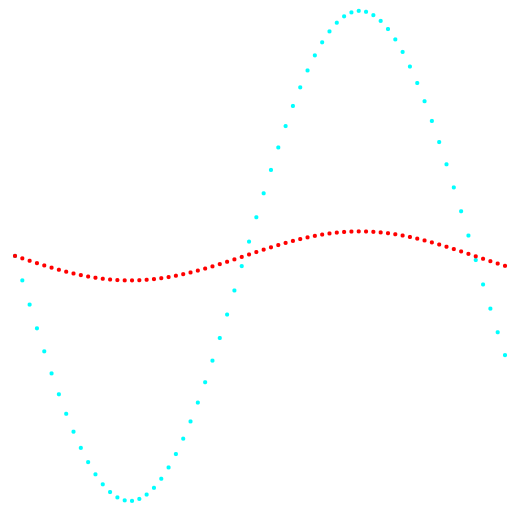
Fig. 1. Proyeksi 1-2 dan klasifikasi data.

Di sebelah kiri adalah metode k-means, di sebelah kanan adalah metode penulis.


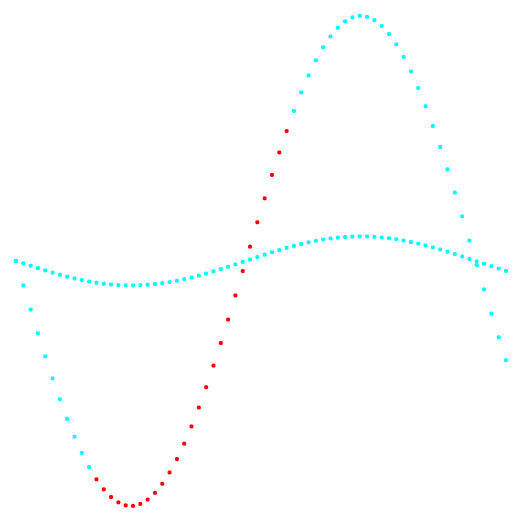
Fig. 2. Proyeksi 2-3 dan klasifikasi data.

Di sebelah kiri adalah metode k-means, di sebelah kanan adalah metode penulis.

Hasil membandingkan dua metode menunjukkan keuntungan yang jelas dari metode penulis dalam kemampuannya untuk mendeteksi kelompok topologi kompleks.

Implementasi perangkat lunak

Metode k-means clustering diimplementasikan secara terprogram sebagai aplikasi web. Bagian komputasi dari aplikasi dikirimkan ke server yang ditulis dalam PHP menggunakan kerangka kerja Zend. Antarmuka aplikasi ditulis menggunakan HTML, CSS, JavaScript, jQuery. Aplikasi ini tersedia di http://svlaboratory.org/application/klaster2 setelah mendaftarkan pengguna baru. Aplikasi ini memungkinkan Anda untuk memvisualisasikan milik benda ke berbagai kelompok dalam bidang koordinat yang diberikan.

Kesimpulan

Metode klasifikasi baru diusulkan. Kelebihan dari metode ini adalah pengenalan kelas topologi yang kompleks, distribusi non-radial, serta kompleksitas algoritma yang lebih sedikit dan tindakan yang lebih sedikit, yang sangat bermanfaat dalam kasus array data yang besar.

Referensi

1. Zagoruyko N.G. Metode data dan analisis pengetahuan yang diterapkan. Novosibirsk: Rumah Penerbitan Institut Matematika, 1999.270 hal.
2. Zagoruyko N.G., Borisova I.A., Kutnenko O.A., Levanov D.A. Deteksi pola dalam susunan data eksperimental // Teknologi komputasi. - 2013.Vol. 18. No. S1. S. 12-20.
3. Shen Furaoa, Tomotaka Ogurab, Osamu Hasegawab, jaringan saraf inkremental mandiri yang ditingkatkan untuk pembelajaran online tanpa pengawasan. Hasegawa Lab, 2007.