Jaringan saraf dan pembelajaran mendalam, bab 5: mengapa jaringan saraf dalam begitu sulit untuk dilatih?

Bayangkan Anda seorang insinyur, dan Anda diminta mengembangkan komputer dari awal. Begitu Anda duduk di kantor, merancang sirkuit logis dengan semua kekuatan Anda, mendistribusikan DAN, ATAU katup, dan sebagainya, - dan tiba-tiba bos Anda datang dan memberi tahu Anda kabar buruknya. Klien baru saja memutuskan untuk menambahkan persyaratan tak terduga ke proyek: skema seluruh komputer tidak boleh lebih dari dua lapisan:



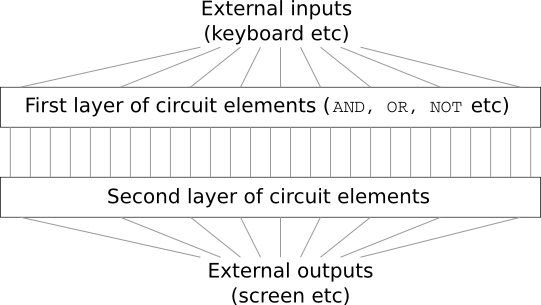
Anda kagum dan memberi tahu bos: "Ya, klien itu gila!"

Bos menjawab, “Saya juga berpikir begitu. Tetapi klien harus mendapatkan apa yang diinginkannya. "

Padahal, dalam arti sempit, klien tidak sepenuhnya gila. Misalkan Anda diizinkan menggunakan gerbang logika khusus yang memungkinkan Anda menghubungkan sejumlah input melalui DAN. Dan Anda diizinkan untuk menggunakan gerbang NAND dengan sejumlah input, yaitu gerbang yang menambahkan banyak input melalui AND, dan kemudian membalikkan hasilnya. Ternyata dengan katup khusus seperti itu Anda dapat menghitung fungsi apa pun hanya dengan sirkuit dua lapis.

Namun, hanya karena sesuatu dapat dilakukan bukan berarti itu layak dilakukan. Dalam praktiknya, ketika memecahkan masalah yang terkait dengan desain sirkuit logika (dan hampir semua masalah algoritmik), kita biasanya memulai dengan menyelesaikan submasalah, dan kemudian secara bertahap mengumpulkan solusi lengkap. Dengan kata lain, kami membangun solusi melalui banyak level abstraksi.

Sebagai contoh, misalkan kita mendesain rangkaian logika untuk mengalikan dua angka. Sangat mungkin bahwa kami ingin membangunnya dari subcircuits yang mengimplementasikan operasi seperti penambahan dua angka. Penambahan subcircuits, pada gilirannya, akan terdiri dari subcircuits yang menambahkan dua bit. Secara kasar, skema kami akan terlihat seperti ini:



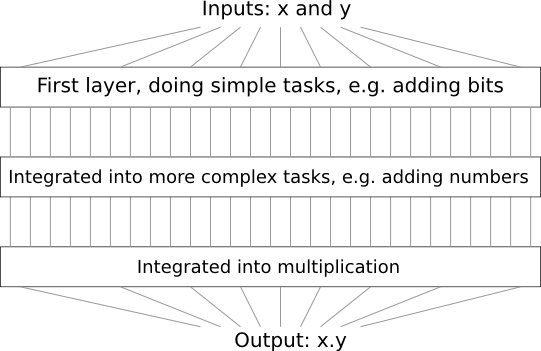
Artinya, rangkaian terakhir mengandung setidaknya tiga lapisan elemen rangkaian. Bahkan, itu mungkin akan memiliki lebih dari tiga lapisan ketika kita memecah subtugas menjadi lebih kecil daripada yang saya jelaskan. Tapi Anda mengerti prinsipnya.

Oleh karena itu, skema yang mendalam memudahkan proses desain. Tetapi mereka membantu tidak hanya dalam desain. Ada bukti matematis bahwa untuk menghitung beberapa fungsi dalam sirkuit yang sangat dangkal, diperlukan untuk menggunakan jumlah elemen yang secara eksponensial lebih besar daripada yang dalam. Sebagai contoh, ada serangkaian karya ilmiah terkenal tahun 1980 - an, di mana ditunjukkan bahwa menghitung paritas seperangkat bit membutuhkan jumlah gerbang yang secara eksponensial lebih besar dengan sirkuit dangkal. Di sisi lain, ketika menggunakan skema dalam, lebih mudah untuk menghitung paritas menggunakan skema kecil: Anda cukup menghitung paritas dari pasangan bit, dan kemudian menggunakan hasilnya untuk menghitung paritas dari pasangan bit, dan seterusnya, dengan cepat mencapai paritas umum. Karena itu, skema yang dalam bisa jauh lebih kuat daripada skema yang dangkal.

Sejauh ini, buku ini telah menggunakan pendekatan neural networks (NS), mirip dengan permintaan klien gila. Hampir semua jaringan tempat kami bekerja memiliki satu lapisan neuron yang tersembunyi (ditambah lapisan input dan output):



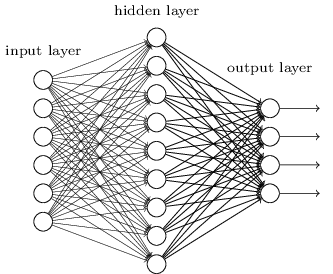
Jaringan sederhana ini ternyata sangat berguna: pada bab-bab sebelumnya kami menggunakan jaringan tersebut untuk mengklasifikasikan angka tulisan tangan dengan akurasi melebihi 98%! Namun, secara intuitif jelas bahwa jaringan dengan banyak lapisan tersembunyi akan jauh lebih kuat:



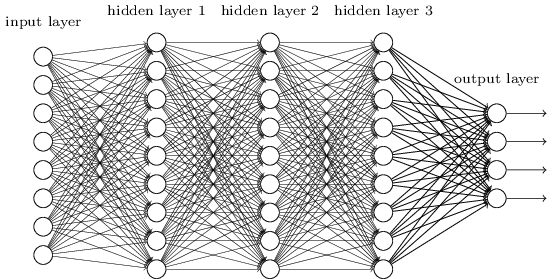
Jaringan tersebut dapat menggunakan lapisan perantara untuk membuat banyak tingkatan abstraksi, seperti halnya dengan skema Boolean kami. Misalnya, dalam hal pengenalan pola, neuron dari lapisan pertama dapat belajar mengenali wajah, neuron dari lapisan kedua - bentuk yang lebih kompleks, misalnya, segitiga atau persegi panjang yang dibuat dari wajah. Kemudian lapisan ketiga akan dapat mengenali bentuk yang lebih kompleks. Dan sebagainya. Sangat mungkin bahwa banyak lapisan abstraksi ini akan memberikan jaringan yang mendalam keuntungan yang meyakinkan dalam memecahkan masalah mengenali pola yang kompleks. Selain itu, seperti dalam kasus sirkuit, ada hasil teoritis yang menegaskan bahwa jaringan yang dalam secara inheren memiliki lebih banyak kemampuan daripada yang dangkal.

Bagaimana kita melatih jaringan saraf yang dalam ini (GNS)? Dalam bab ini, kami akan mencoba untuk melatih STS menggunakan kuda kami di antara algoritma pelatihan - gradien keturunan penurunan propagasi stochastic. Namun, kami akan menghadapi masalah - STS kami tidak akan bekerja lebih baik (jika sama sekali melampaui) daripada yang dangkal.

Kegagalan ini tampak aneh mengingat diskusi di atas. Tetapi alih-alih menyerah pada STS, kita akan mempelajari lebih dalam masalah ini dan mencoba memahami mengapa STS sulit untuk dilatih. Ketika kita melihat lebih dekat masalah ini, kita akan menemukan bahwa berbagai lapisan dalam STS belajar dengan kecepatan yang sangat berbeda. Secara khusus, ketika lapisan terakhir dari jaringan dilatih dengan baik, yang pertama sering macet selama pelatihan, dan hampir tidak belajar apa-apa. Dan itu bukan hanya nasib buruk. Kami akan menemukan alasan mendasar untuk memperlambat pembelajaran yang terkait dengan penggunaan teknik pembelajaran berbasis gradien.

Mengalami masalah ini lebih dalam, kami menemukan bahwa fenomena yang berlawanan juga dapat terjadi: lapisan awal dapat belajar dengan baik, dan yang kemudian terjebak. Bahkan, kami akan menemukan ketidakstabilan internal yang terkait dengan pelatihan gradient descent di NSs multilayer yang dalam. Dan karena ketidakstabilan ini, baik lapisan awal atau akhir sering terjebak dalam pelatihan.

Semua ini terdengar sangat tidak menyenangkan. Tetapi ketika terjun ke dalam kesulitan-kesulitan ini, kita dapat mulai mengembangkan gagasan tentang apa yang perlu dilakukan untuk pelatihan STS yang efektif. Oleh karena itu, studi ini akan menjadi persiapan yang baik untuk bab selanjutnya, di mana kita akan menggunakan pembelajaran mendalam untuk mendekati masalah pengenalan citra.

Masalah gradien memudar

Jadi apa yang salah ketika kami mencoba untuk melatih jaringan yang dalam?

Untuk menjawab pertanyaan ini, kami kembali ke jaringan yang hanya berisi satu lapisan tersembunyi. Seperti biasa, kita akan menggunakan masalah klasifikasi digit MNIST sebagai kotak pasir untuk belajar dan bereksperimen.

Jika Anda ingin mengulangi semua langkah ini di komputer Anda, Anda harus menginstal Python 2.7, perpustakaan Numpy, dan salinan kode yang dapat diambil dari repositori:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git 

Anda dapat melakukannya tanpa git dengan hanya mengunduh data dan kode . Pergi ke subdirektori src dan dari shell python memuat data MNIST:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Konfigurasikan jaringan:

 >>> import network2 >>> net = network2.Network([784, 30, 10]) 

Jaringan seperti itu memiliki 784 neuron pada lapisan input, sesuai dengan 28 × 28 = 784 piksel dari gambar input. Kami menggunakan 30 neuron tersembunyi dan 10 akhir pekan, yang sesuai dengan sepuluh opsi klasifikasi yang memungkinkan untuk angka-angka MNIST ('0', '1', '2', ..., '9').

Mari kita coba untuk melatih jaringan kita selama 30 zaman penuh menggunakan paket mini 10 contoh pelatihan sekaligus, kecepatan belajar η = 0,1 dan parameter regularisasi λ = 5.0. Selama pelatihan, kami akan melacak keakuratan klasifikasi melalui validation_data:

 >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Kami mendapatkan akurasi klasifikasi 96,48% (atau lebih - jumlahnya akan bervariasi dengan peluncuran yang berbeda), sebanding dengan hasil kami sebelumnya dengan pengaturan yang sama.

Mari kita tambahkan layer tersembunyi lainnya, juga mengandung 30 neuron, dan coba latih jaringan dengan hyperparameter yang sama:

 >>> net = network2.Network([784, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Akurasi klasifikasi meningkat menjadi 96,90%. Ini menginspirasi - sedikit peningkatan kedalaman membantu. Mari kita tambahkan lapisan tersembunyi lain dari 30 neuron:

 >>> net = network2.Network([784, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Itu tidak membantu. Hasilnya bahkan jatuh ke 96,57%, nilai yang dekat dengan jaringan dangkal asli. Dan jika kita menambahkan lapisan tersembunyi lainnya:

 >>> net = network2.Network([784, 30, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Kemudian akurasi klasifikasi akan kembali turun, sudah menjadi 96,53%. Secara statistik, penurunan ini mungkin tidak signifikan, tetapi tidak ada yang baik tentang itu.

Perilaku ini sepertinya aneh. Tampaknya secara intuitif bahwa lapisan tersembunyi tambahan akan membantu jaringan mempelajari fungsi klasifikasi yang lebih kompleks, dan lebih baik mengatasi tugas tersebut. Tentu saja, hasilnya tidak boleh memburuk, karena dalam kasus terburuk, lapisan tambahan tidak akan melakukan apa pun. Namun, ini tidak terjadi.

Jadi apa yang sedang terjadi? Mari kita asumsikan bahwa lapisan tersembunyi tambahan dapat membantu pada prinsipnya, dan masalahnya adalah bahwa algoritma pelatihan kami tidak menemukan nilai yang benar untuk bobot dan penyeimbang. Kami ingin memahami apa yang salah dengan algoritma kami, dan bagaimana memperbaikinya.

Untuk memahami apa yang salah, mari kita visualisasikan proses pembelajaran jaringan. Di bawah ini, saya membangun bagian dari jaringan [784,30,30,10], di mana ada dua lapisan tersembunyi, yang masing-masing memiliki 30 neuron tersembunyi. Pada diagram, masing-masing neuron memiliki bilah yang menunjukkan tingkat perubahan dalam proses belajar jaringan. Balok yang besar berarti bahwa bobot dan perpindahan neuron berubah dengan cepat, dan yang kecil berarti bahwa mereka berubah secara perlahan. Lebih tepatnya, bilah menunjukkan gradien ∂C / ∂b dari neuron, yaitu laju perubahan biaya sehubungan dengan perpindahan. Dalam bab 2, kami melihat bahwa nilai gradien ini mengontrol tidak hanya laju perubahan perpindahan selama pelatihan, tetapi juga laju perubahan bobot neuron input. Jangan khawatir jika Anda tidak dapat mengingat detail ini: Anda hanya perlu mengingat bahwa palang-palang ini menunjukkan seberapa cepat bobot dan perpindahan neuron berubah selama pelatihan jaringan.

Untuk menyederhanakan diagram, saya hanya menggambar enam neuron atas dalam dua lapisan tersembunyi. Saya menurunkan neuron yang masuk karena tidak memiliki bobot atau bias. Saya juga menghilangkan neuron keluaran, karena kami membandingkan dua lapisan, dan masuk akal untuk membandingkan lapisan dengan jumlah neuron yang sama. Diagram dibangun menggunakan program generate_gradient.py di awal pelatihan, yaitu, segera setelah jaringan diinisialisasi.



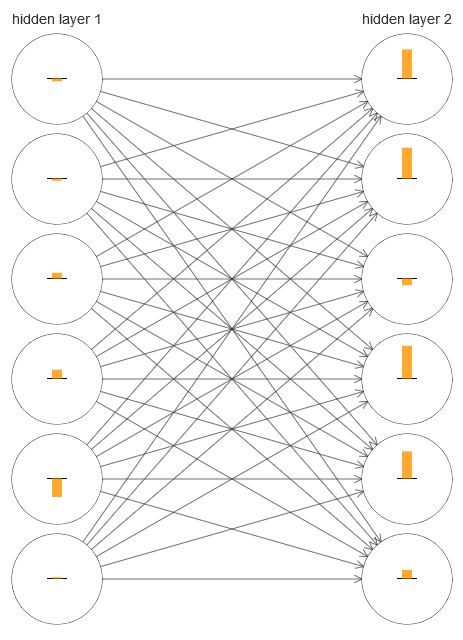
Jaringan diinisialisasi secara kebetulan, jadi keragaman dalam kecepatan pelatihan neuron ini tidak mengejutkan. Namun, segera menangkap mata bahwa pada lapisan kedua yang tersembunyi, strip pada dasarnya jauh lebih banyak daripada yang pertama. Akibatnya, neuron di lapisan kedua akan belajar lebih cepat daripada di lapisan pertama. Apakah ini kebetulan, atau apakah neuron di lapisan kedua cenderung belajar secara umum lebih cepat daripada neuron di lapisan pertama?

Untuk mengetahui dengan tepat, akan baik untuk memiliki cara umum membandingkan kecepatan belajar di lapisan tersembunyi pertama dan kedua. Untuk melakukan ini, mari kita menyatakan gradien sebagai δ ^l _j = ∂C / ∂b ^l _j , yaitu, sebagai gradien neuron No. j di lapisan No. l. Pada bab kedua, kami menyebutnya "kesalahan", tetapi di sini saya akan menyebutnya "gradien". Secara informal - karena nilai ini tidak secara eksplisit memasukkan turunan sebagian dari biaya berdasarkan berat, ∂C / ∂w. Gradien δ ¹ dapat dianggap sebagai vektor yang unsur-unsurnya menentukan seberapa cepat lapisan tersembunyi pertama belajar, dan δ ² sebagai vektor yang unsur-unsurnya menentukan seberapa cepat lapisan tersembunyi kedua belajar. Kami menggunakan panjang vektor-vektor ini sebagai perkiraan perkiraan kecepatan pembelajaran lapisan. Misalnya, panjangnya || δ ¹ || mengukur kecepatan belajar dari lapisan tersembunyi pertama, dan panjang || δ ² || mengukur kecepatan belajar dari lapisan tersembunyi kedua.

Dengan definisi dan konfigurasi yang sama seperti di atas, kami menemukan bahwa || δ ¹ || = 0,07, dan || δ ² || = 0,31. Ini mengkonfirmasi kecurigaan kami: neuron di lapisan tersembunyi kedua belajar lebih cepat dari neuron di lapisan tersembunyi pertama.

Apa yang terjadi jika kita menambahkan lebih banyak lapisan tersembunyi? Dengan tiga lapisan tersembunyi dalam jaringan [784,30,30,30,10] kecepatan belajar yang sesuai adalah 0,012, 0,060 dan 0,283. Sekali lagi, lapisan tersembunyi pertama belajar lebih lambat dari yang terakhir. Tambahkan lapisan tersembunyi lainnya dengan 30 neuron. Dalam hal ini, kecepatan belajar yang sesuai adalah 0,003, 0,017, 0,070 dan 0,285. Polanya dipertahankan: lapisan awal belajar lebih lambat daripada yang kemudian.

Kami mempelajari kecepatan belajar di awal - tepat setelah jaringan diinisialisasi. Bagaimana kecepatan ini berubah saat Anda belajar? Mari kita kembali dan melihat jaringan dengan dua lapisan tersembunyi. Kecepatan belajar berubah seperti ini:



Untuk mendapatkan hasil ini, saya menggunakan keturunan gradient batch dengan 1000 gambar pelatihan dan pelatihan selama 500 era. Ini sedikit berbeda dari prosedur kami yang biasa - Saya tidak menggunakan paket mini dan hanya mengambil 1000 gambar pelatihan, alih-alih set lengkap 50.000 buah. Saya tidak mencoba menipu dan menipu Anda, tetapi ternyata menggunakan stochastic gradient descent dengan paket-mini membawa lebih banyak noise pada hasilnya (tetapi jika Anda meratakan noise, hasilnya mirip). Dengan menggunakan parameter yang saya pilih, mudah untuk memperlancar hasilnya sehingga kita bisa melihat apa yang terjadi.

Bagaimanapun, seperti yang kita lihat, dua lapisan mulai berlatih dengan dua kecepatan yang sangat berbeda (yang sudah kita ketahui). Kemudian kecepatan kedua lapisan turun sangat cepat, setelah itu terjadi rebound. Namun, selama ini, lapisan tersembunyi pertama belajar lebih lambat dari lapisan kedua.

Bagaimana dengan jaringan yang lebih kompleks? Berikut ini adalah hasil dari percobaan serupa, tetapi dengan jaringan dengan tiga lapisan tersembunyi [784,30,30,30,10]:



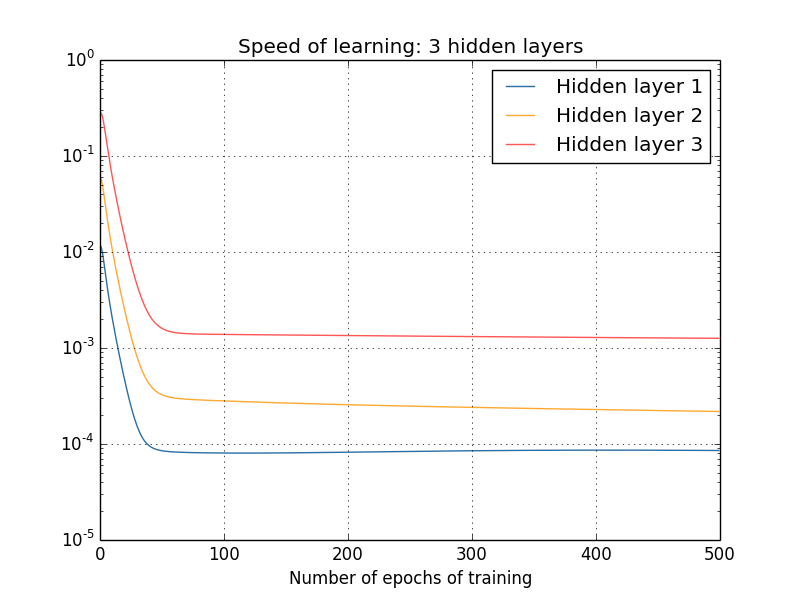
Dan lagi, lapisan tersembunyi pertama belajar lebih lambat dari yang terakhir. Akhirnya, mari kita coba menambahkan lapisan tersembunyi keempat (jaringan [784,30,30,30,30,10]), dan lihat apa yang terjadi ketika dilatih:



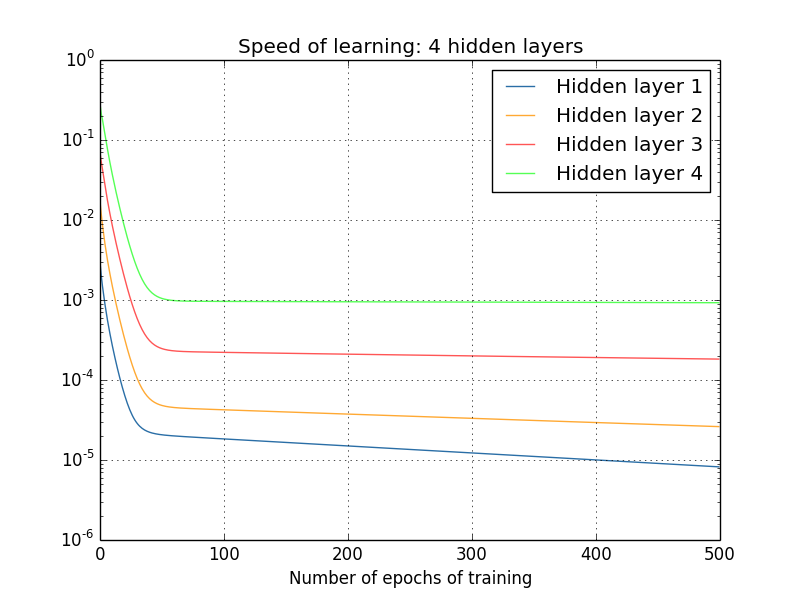
Dan lagi, lapisan tersembunyi pertama belajar lebih lambat dari yang terakhir. Dalam hal ini, lapisan tersembunyi pertama belajar sekitar 100 kali lebih lambat dari yang terakhir. Tidak heran kami mengalami masalah dalam mempelajari jaringan ini!

Kami melakukan pengamatan penting: setidaknya di beberapa GNS, gradien berkurang ketika bergerak ke arah yang berlawanan di sepanjang lapisan tersembunyi. Yaitu, neuron di lapisan pertama dilatih jauh lebih lambat daripada neuron di lapisan terakhir. Dan meskipun kami mengamati efek ini hanya dalam satu jaringan, ada alasan mendasar mengapa ini terjadi di banyak NS. Fenomena ini dikenal sebagai "masalah gradien hilang" (lihat karya 1 , 2 ).

Mengapa ada masalah gradien fading? Apakah ada cara untuk menghindarinya? Bagaimana kita menghadapinya saat melatih STS? Bahkan, kita akan segera mengetahui bahwa itu tidak bisa dihindari, meskipun alternatifnya tidak terlihat sangat menarik baginya: kadang-kadang di lapisan pertama gradiennya jauh lebih besar! Ini sudah merupakan masalah pertumbuhan gradien eksplosif, dan itu tidak lebih baik di dalamnya daripada dalam masalah gradien menghilang. Secara umum, ternyata gradien dalam STS tidak stabil, dan rentan terhadap pertumbuhan eksplosif atau menghilang di lapisan pertama. Ketidakstabilan ini adalah masalah mendasar untuk pelatihan GNS gradien. Inilah yang perlu kita pahami, dan mungkin menyelesaikannya entah bagaimana.

Salah satu reaksi terhadap gradien fading (atau tidak stabil) adalah berpikir apakah ini sebenarnya masalah serius? Mari kita sejenak mengalihkan perhatian dari NS, dan bayangkan bahwa kita sedang mencoba untuk meminimalkan fungsi f (x) secara numerik dari satu variabel. Bukankah lebih baik jika turunan f ′ (x) kecil? Bukankah ini berarti kita sudah dekat dengan yang ekstrem? Dan dengan cara yang sama, apakah gradien kecil di lapisan pertama GNS tidak berarti bahwa kita tidak perlu lagi menyesuaikan bobot dan perpindahan secara signifikan?

Tentu saja tidak. Ingatlah bahwa kami secara acak menginisialisasi bobot dan offset jaringan. Sangat tidak mungkin bahwa bobot dan campuran asli kami akan bekerja dengan baik dengan apa yang kami inginkan dari jaringan kami. Sebagai contoh spesifik, perhatikan lapisan pertama bobot dalam jaringan [784,30,30,30,10], yang mengklasifikasikan angka-angka MNIST. Inisialisasi acak berarti bahwa lapisan pertama mengeluarkan sebagian besar informasi tentang gambar yang masuk. Bahkan jika lapisan selanjutnya dilatih dengan hati-hati, akan sangat sulit bagi mereka untuk menentukan pesan yang masuk, hanya karena kurangnya informasi. Oleh karena itu, sangat mustahil untuk membayangkan bahwa lapisan pertama tidak perlu dilatih. Jika kita akan melatih STS, kita perlu memahami bagaimana menyelesaikan masalah gradien yang menghilang.

Apa yang menyebabkan masalah gradien fading? Gradien yang tidak stabil di GNS

Untuk memahami bagaimana masalah gradien menghilang muncul, pertimbangkan NS paling sederhana: dengan hanya satu neuron di setiap lapisan. Berikut adalah jaringan dengan tiga lapisan tersembunyi:



Di sini w ₁ , w ₂ , ... adalah bobot, b ₁ , b ₂ , ... adalah perpindahan, C adalah fungsi biaya tertentu. Sekadar mengingatkan Anda, saya akan mengatakan bahwa output a _j dari neuron No. j sama dengan σ (z _j ), di mana σ adalah fungsi aktivasi sigmoid yang biasa, dan z _j = w _j a _{j - 1} + b _j adalah input tertimbang dari neuron. Saya menggambarkan fungsi biaya pada akhir untuk menekankan bahwa biaya adalah fungsi dari output jaringan, dan ₄ : jika output nyata dekat dengan apa yang Anda inginkan, maka biayanya akan kecil, dan jika jauh, maka akan menjadi besar.

Kami mempelajari gradien ∂C / ∂b _{1 yang} terkait dengan neuron tersembunyi pertama. Kami menemukan ekspresi untuk ∂C / ∂b ₁ dan, setelah mempelajarinya, kami akan mengerti mengapa masalah gradien hilang muncul.

Kita mulai dengan mendemonstrasikan ekspresi untuk ∂C / ∂b ₁ . Ini terlihat tidak dapat ditembus, tetapi sebenarnya strukturnya sederhana, dan saya akan segera menjelaskannya. Inilah ungkapan ini (untuk saat ini, abaikan jaringan itu sendiri dan perhatikan bahwa σ hanyalah turunan dari fungsi σ):



Struktur dari ekspresi adalah sebagai berikut: untuk setiap neuron dalam jaringan terdapat istilah multiplikasi σ ′ (z _j ), untuk setiap bobot ada _wj , dan ada juga suku terakhir, ∂C / ∂a ₄ , sesuai dengan fungsi biaya. Perhatikan bahwa saya menempatkan anggota yang sesuai di atas bagian jaringan yang sesuai. Oleh karena itu, jaringan itu sendiri adalah aturan mnemonik untuk berekspresi.

Anda dapat mengambil ungkapan ini pada iman dan melewatkan diskusi langsung ke tempat di mana dijelaskan bagaimana hubungannya dengan masalah gradien pudar. Tidak ada yang salah dengan ini, karena ungkapan ini adalah kasus khusus dari diskusi kita tentang backpropagation. Namun, mudah untuk menjelaskan kesetiaannya, sehingga akan sangat menarik (dan mungkin instruktif) bagi Anda untuk mempelajari penjelasan ini.

Bayangkan kita melakukan perubahan kecil pada Δb ₁ ke offset b ₁ . Ini akan mengirimkan serangkaian perubahan berjenjang di seluruh jaringan. Pertama, ini akan menyebabkan output dari neuron tersembunyi pertama Δa ₁ berubah. Ini, pada gilirannya, memaksa 2z ₂ untuk mengubah input tertimbang ke neuron tersembunyi kedua. Kemudian akan ada perubahan Δa ₂ dalam output neuron tersembunyi kedua. Dan seterusnya, hingga perubahan ΔC pada nilai output. Ternyata itu:

$$

$$\ frac {\ partial C} {\ partial b_1} \ approx \ frac {\ Delta C} {\ Delta b_1} \ tag {114}$$

Ini menunjukkan bahwa kita dapat menurunkan ekspresi gradien ∂C / ∂b ₁ , dengan hati-hati memantau pengaruh setiap langkah dalam kaskade ini.

Untuk melakukan ini, mari kita pikirkan bagaimana 1b ₁ menyebabkan output a _{1 dari} neuron tersembunyi pertama berubah. Karenanya, kita memiliki ₁ = σ (z ₁ ) = σ (w ₁ a ₀ + b ₁ )

$$

$$\ Delta a_1 \ approx \ frac {\ partial \ sigma (w_1 a_0 + b_1)} {\ partial b_1} \ Delta b_1 \ tag {115}$$

$$

$$= \ sigma '(z_1) \ Delta b_1 \ tag {116}$$

Istilah σ ′ (z ₁ ) harus terlihat familier: ini adalah istilah pertama dari ekspresi kami untuk gradien ∂C / ∂b ₁ . Secara intuitif, ini mengubah perubahan offsetb ₁ offset menjadi perubahan Δa _{1 dari} aktivasi output. Perubahan Δa ₁ pada gilirannya menyebabkan perubahan pada input tertimbang z ₂ = w ₂ a ₁ + b _{2 dari} neuron tersembunyi kedua:

$$

$$\ Delta z_2 \ approx \ frac {\ partial z_2} {\ partial a_1} \ Delta a_1 \ tag {117}$$

$$

$$= w_2 \ Delta a_1 \ tag {118}$$

Menggabungkan ekspresi untuk Δz ₂ dan Δa ₁ , kita melihat bagaimana perubahan dalam bias b ₁ merambat di sepanjang jaringan dan mempengaruhi z ₂ :

$$

$$\ Delta z_2 \ approx \ sigma '(z_1) w_2 \ Delta b_1 \ tag {119}$$

Dan ini juga harus familier: ini adalah dua istilah pertama dalam ekspresi yang kami nyatakan untuk gradien ∂C / ∂b ₁ .

Ini dapat dilanjutkan lebih lanjut dengan memantau bagaimana perubahan disebarkan ke seluruh jaringan. Pada setiap neuron kita memilih istilah σ ′ (z _j ), dan melalui setiap bobot kita memilih istilah w _j . Sebagai hasilnya, diperoleh ekspresi yang menghubungkan perubahan akhir ΔC dari fungsi biaya dengan perubahan awal Δb _{1 dari} bias:

$$

$$\ Delta C \ approx \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ partial C} {\ partial a_4} \ Delta b_1 \ tag {120}$$

Membagi dengan Δb ₁ , kita benar-benar mendapatkan ekspresi yang diinginkan untuk gradien:

$$

$$\ frac {\ partial C} {\ partial b_1} = \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ partial C} {\ partial a_4} \ tag { 121}$$

Mengapa ada masalah gradien fading?

Untuk memahami mengapa masalah gradien yang hilang muncul, mari kita tuliskan secara rinci seluruh ekspresi kami untuk gradien:

$$

$$\ frac {\ partial C} {\ partial b_1} = \ sigma '(z_1) \ w_2 \ sigma' (z_2) \ w_3 \ sigma '(z_3) \, w_4 \ sigma' (z_4) \ \ frac {\ partial C} {\ partial a_4} \ tag {122}$$

Selain istilah terakhir, ungkapan ini adalah produk dari istilah _wj σ ′ (z _j ). Untuk memahami bagaimana masing-masing dari mereka berperilaku, kita melihat grafik fungsi σ:



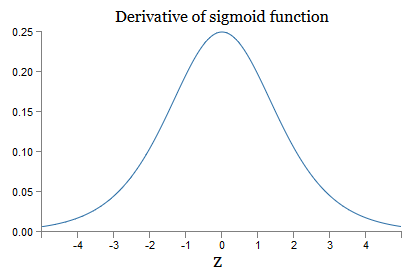
Grafik mencapai maksimum pada titik σ ′ (0) = 1/4. Jika kita menggunakan pendekatan standar untuk menginisialisasi bobot jaringan, maka kita memilih bobot menggunakan distribusi Gaussian, yaitu, rata-rata kuadrat nol dan standar deviasi 1. Oleh karena itu, biasanya bobot akan memenuhi ketidaksetaraan | w _j | <1. Membandingkan semua pengamatan ini, kita melihat bahwa istilah w _j σ ′ (z _j ) biasanya akan memenuhi ketidaksetaraan | w _j σ ′ (z _j ) | <1/4. Dan jika kita mengambil produk dari himpunan istilah tersebut, maka itu akan menurun secara eksponensial: semakin banyak istilah, semakin kecil produk. Itu mulai tampak seperti solusi yang mungkin untuk masalah gradien yang menghilang.

Untuk menulis ini lebih akurat, kami membandingkan ekspresi untuk ∂C / ∂b ₁ dengan ekspresi gradien sehubungan dengan offset berikutnya, misalnya, ∂C / ∂b ₃ . Tentu saja, kami tidak menuliskan ekspresi terperinci untuk ∂C / ∂b ₃ , tetapi mengikuti hukum yang sama seperti yang dijelaskan di atas untuk ∂C / ∂b ₁ . Dan ini adalah perbandingan dari dua ekspresi:



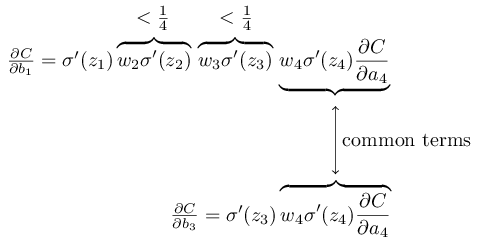
Mereka memiliki beberapa anggota yang sama. Namun, gradien ∂C / ∂b ₁ mencakup dua istilah tambahan, yang masing-masing memiliki bentuk w _j σ ′ (z _j ). Seperti yang telah kita lihat, istilah seperti itu biasanya tidak melebihi 1/4. Oleh karena itu, gradien ∂C / ∂b ₁ biasanya akan menjadi 16 (atau lebih) kali lebih kecil dari ∂C / ∂b ₃ . Dan ini adalah penyebab utama dari masalah gradien yang hilang.

Tentu saja, ini tidak akurat, tetapi bukti informal dari masalah tersebut. Ada beberapa peringatan. Secara khusus, orang mungkin tertarik pada apakah bobot akan meningkat selama pelatihan. Jika ini terjadi, istilah w _j σ ′ (z _j ) dalam produk tidak akan lagi memenuhi ketidaksetaraan | w _j σ ′ (z _j ) | <1/4. Dan jika mereka ternyata cukup besar, lebih dari 1, maka kita tidak akan lagi memiliki masalah gradien pudar. Sebaliknya, gradien akan tumbuh secara eksponensial saat Anda bergerak kembali melalui lapisan. Dan alih-alih masalah gradien yang menghilang, kita mendapatkan masalah pertumbuhan gradien eksplosif.

Masalah pertumbuhan gradien eksplosif

Mari kita lihat contoh spesifik dari gradien eksplosif. Contohnya akan agak buatan: Saya akan menyesuaikan parameter jaringan untuk menjamin terjadinya pertumbuhan eksplosif. Tetapi meskipun contohnya adalah tiruan, nilai tambahnya adalah ia dengan jelas menunjukkan bahwa pertumbuhan gradien yang meledak bukanlah kemungkinan hipotetis, tetapi itu benar-benar dapat terjadi.

Untuk pertumbuhan gradien eksplosif, Anda perlu mengambil dua langkah. Pertama, kami memilih bobot besar di seluruh jaringan, misalnya, w1 = w2 = w3 = w4 = 100. Kemudian kami memilih shift sedemikian sehingga istilah σ ′ (z _j ) tidak terlalu kecil. Dan ini cukup mudah dilakukan: kita hanya perlu memilih perpindahan seperti itu sehingga input tertimbang dari setiap neuron adalah zj = 0 (dan kemudian σ σ (z _j ) = 1/4). Karena itu, misalnya, kita perlu z ₁ = w ₁ a ₀ + b ₁ = 0. Ini dapat dicapai dengan menetapkan b ₁ = −100 ∗ a ₀ . Ide yang sama dapat digunakan untuk memilih offset lain. Akibatnya, kita akan melihat bahwa semua istilah w _j σ ′ (z _j ) ternyata sama dengan 100 ∗ 14 = 25. Dan kemudian kita mendapatkan pertumbuhan gradien eksplosif.

Masalah gradien tidak stabil

Masalah mendasar bukanlah masalah gradien yang menghilang atau pertumbuhan gradien yang eksplosif. Itu adalah bahwa gradien pada lapisan pertama adalah produk anggota dari semua lapisan lainnya. Dan ketika ada banyak lapisan, situasinya pada dasarnya menjadi tidak stabil. Dan satu-satunya cara agar semua lapisan dapat belajar dengan kecepatan yang sama adalah memilih anggota pekerjaan yang akan menyeimbangkan satu sama lain. Dan dengan tidak adanya mekanisme atau alasan keseimbangan seperti itu, kecil kemungkinan hal ini akan terjadi secara kebetulan.Singkatnya, masalah sebenarnya adalah NS menderita masalah gradien yang tidak stabil. Dan pada akhirnya, jika kita menggunakan teknik pembelajaran berbasis gradien standar, lapisan jaringan yang berbeda akan belajar dengan kecepatan yang sangat berbeda.

Berolahraga

• , |σ′(z)|<1/4. , , . ?

Kita telah melihat bahwa gradien dapat menghilang atau tumbuh secara eksplosif di lapisan pertama jaringan yang dalam. Bahkan, ketika menggunakan neuron sigmoid, gradien biasanya akan hilang. Untuk memahami alasannya, pertimbangkan lagi ungkapan | wσ ′ (z) |. Untuk menghindari masalah gradien yang menghilang, kita perlu | wσ ′ (z) | ≥1. Anda dapat memutuskan bahwa ini mudah dicapai dengan nilai w yang sangat besar. Namun, pada kenyataannya itu tidak sesederhana itu. Alasannya adalah bahwa istilah σ ′ (z) juga tergantung pada w: σ ′ (z) = σ ′ (wa + b), di mana a adalah aktivasi input. Dan jika kita membuat w besar, kita perlu mencoba untuk tidak membuat σ ′ (wa + b) kecil secara paralel. Dan ini ternyata menjadi batasan serius. Alasannya adalah bahwa ketika kita membuat w besar, kita membuat wa + b sangat besar. Jika Anda melihat grafik σ ′, dapat dilihat bahwa ini membawa kita ke "sayap" dari fungsi σ ′,di mana ia mengambil nilai yang sangat kecil. Dan satu-satunya cara untuk menghindari ini adalah menjaga aktivasi yang masuk dalam kisaran nilai yang cukup sempit. Terkadang ini terjadi secara tidak sengaja. Tetapi lebih sering ini tidak terjadi. Oleh karena itu, dalam kasus umum, kami memiliki masalah gradien hilang.

• |wσ′(wa+b)|. , |wσ′(wa+b)|≥1. , , |w|≥4.
• , |w|≥4, , |wσ′(wa+b)|≥1.
• , , ,

  $$

  $$\frac{2}{|w|} \ln\left( \frac{|w|(1+\sqrt{1-4/|w|})}{2}-1\right) \tag{123}$$
• , |w|≈6.9, ≈0,45. , , , .
• . x, w ₁ , b w ₂ . , , , w ₂ σ(w ₁ x+b)≈x for x∈[0,1]. , , ( ). : x=1/2+Δ, , w ₁ , w ₁ Δ .

Kami mempelajari jaringan mainan dengan hanya satu neuron di setiap lapisan tersembunyi. Bagaimana dengan jaringan dalam yang lebih kompleks yang memiliki banyak neuron di setiap lapisan tersembunyi?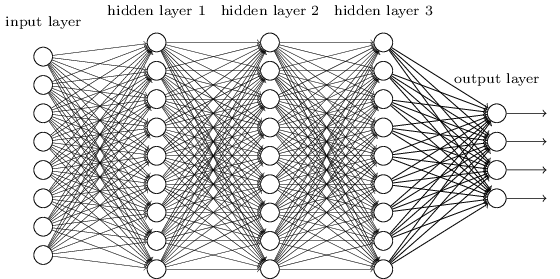



Bahkan, banyak hal yang sama terjadi di jaringan seperti itu. Sebelumnya dalam bab tentang propagasi belakang, kita melihat bahwa gradien di lapisan # l dari jaringan dengan lapisan L ditentukan sebagai:

$$

$$\delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C \tag{124}$$

Di sini Σ ′ (z ^l ) adalah matriks diagonal, yang unsur-unsurnya adalah nilai-nilai σ ′ (z) untuk input tertimbang lapisan No. l. w ^l adalah matriks bobot untuk berbagai lapisan. Dan ∇ _a adalah vektor turunan parsial dari C sehubungan dengan aktivasi keluaran.

Ungkapan ini jauh lebih rumit daripada kasus dengan satu neuron. Namun, jika Anda melihat lebih dekat, esensinya akan sangat mirip, dengan sekelompok pasangan bentuk ( ^wj ) ^T Σ ′ (z ^j ). Selain itu, matriks Σ ′ (z ^j ) secara diagonal memiliki nilai kecil, tidak lebih dari 1/4. Jika matriks bobot ^wj tidak terlalu besar, setiap suku tambahan ( ^wj ) ^T Σ ′ (z ^l) cenderung mengurangi vektor gradien, yang mengarah ke gradien yang menghilang. Dalam kasus umum, sejumlah besar istilah penggandaan menyebabkan gradien yang tidak stabil, seperti pada contoh kami sebelumnya. Dalam prakteknya, secara empiris biasanya dalam jaringan sigmoid, gradien pada lapisan pertama menghilang dengan cepat secara eksponensial. Akibatnya, belajar di lapisan ini melambat. Dan perlambatan bukanlah kecelakaan atau ketidaknyamanan: itu adalah konsekuensi mendasar dari pendekatan yang kami pilih untuk belajar.

Hambatan lain untuk pembelajaran yang mendalam

Dalam bab ini, saya fokus pada gradien fading - dan lebih umum kasus gradien tidak stabil - sebagai hambatan untuk pembelajaran yang mendalam. Faktanya, gradien yang tidak stabil hanyalah salah satu kendala bagi pengembangan pertahanan sipil, walaupun merupakan hal yang penting dan mendasar. Bagian penting dari penelitian saat ini adalah mencoba untuk lebih memahami masalah yang mungkin timbul dalam pengajaran GO. Saya tidak akan menjelaskan secara rinci semua karya ini, tetapi saya ingin secara singkat menyebutkan beberapa karya untuk memberi Anda gambaran tentang beberapa pertanyaan yang diajukan oleh orang-orang.

Sebagai contoh pertama di tahun 2010bukti ditemukan bahwa penggunaan fungsi aktivasi sigmoid dapat menyebabkan masalah dengan belajar NS. Secara khusus, bukti ditemukan bahwa penggunaan sigmoid akan mengarah pada fakta bahwa aktivasi lapisan tersembunyi terakhir selama pelatihan akan jenuh di wilayah 0, yang secara serius akan memperlambat pelatihan. Beberapa fungsi aktivasi alternatif telah diusulkan yang tidak terlalu menderita dari masalah saturasi (lihat juga makalah diskusi lain ).

Sebagai contoh pertama, pada tahun 2013, efek inisialisasi acak bobot dan grafik momentum dalam penurunan gradien stokastik berdasarkan impuls dipelajari pada GO. Dalam kedua kasus, pilihan yang baik secara signifikan memengaruhi kemampuan untuk melatih STS.

Contoh-contoh ini menunjukkan bahwa pertanyaan "Mengapa STS begitu sulit untuk dilatih?" sangat rumit. Dalam bab ini, kami fokus pada ketidakstabilan yang terkait dengan pelatihan gradien GNS. Hasil dari dua paragraf sebelumnya menunjukkan bahwa pilihan fungsi aktivasi, metode inisialisasi bobot, dan bahkan rincian pelaksanaan pelatihan berdasarkan gradient descent juga berperan. Dan, tentu saja, pilihan arsitektur jaringan dan hyperparameter lainnya akan menjadi penting. Oleh karena itu, banyak faktor dapat berperan dalam kesulitan mempelajari jaringan yang dalam, dan masalah memahami faktor-faktor ini adalah subjek penelitian yang sedang berlangsung. Tetapi semua ini tampaknya agak suram dan menginspirasi pesimisme. Namun, ada kabar baik - di bab berikutnya kami akan membungkus semuanya demi kami, dan kami akan mengembangkan beberapa pendekatan di GO,yang sampai batas tertentu akan dapat mengatasi atau menghindari semua masalah ini.