Quantum, atau di sana dan di belakang: algoritma baru untuk mempelajari transisi kuantum-klasik

Banyak yang percaya bahwa hanya fisika kuantum yang bisa lebih rumit daripada fisika klasik. Namun, jauh lebih sulit untuk mempelajari sistem yang, demikian, di persimpangan dua dunia ini. Jika semakin banyak partikel yang ditambahkan ke sistem kuantum, maka ia akan mulai kehilangan sifat kuantumnya dan berubah menjadi yang lebih klasik. Proses ini disebut transisi kuantum-klasik. Komputer klasik tidak akan cukup untuk mempelajari sistem seperti itu, karena para ilmuwan dari Los Alamos National Laboratory telah mengusulkan algoritma mereka sendiri, yang, ditambah dengan komputer kuantum dari beberapa ratus qubit, dapat memecahkan rahasia transisi kuantum-klasik. Bagaimana algoritme bekerja, mengapa rumus yang lebih sedikit berarti lebih baik dan apa penerapan algoritma ini dalam praktik? Ini dan bukan saja kita belajar dari laporan kelompok riset. Ayo pergi.

Dasar studi

Transisi kuantum-klasik, jika dibesar-besarkan, adalah proses dekoherensi ketika sistem kuantum kehilangan koherensinya, yaitu memperoleh fitur klasik. Proses ini dapat terjadi karena sejumlah alasan, di antaranya yang paling jelas adalah interaksi sistem kuantum dan lingkungan. Diyakini juga bahwa proses ini adalah batu yang menjadi dasar proses mewujudkan komputer kuantum.

Ada banyak metode untuk memerangi dekoherensi, yang satu lebih menghibur daripada yang lain, tetapi secara total mereka dapat dibagi menjadi dua kategori: isolasi dan implementasi. Dalam kasus pertama, para ilmuwan berusaha untuk mengisolasi sistem kuantum dari lingkungan, menggunakan suhu yang sangat rendah dan / atau vakum tinggi. Dalam kasus kedua, koreksi (kode) dimasukkan ke dalam algoritma perhitungan kuantum, yang akan tahan terhadap kesalahan yang timbul karena dekoherensi. Metode-metode ini bekerja, tidak ada yang menyangkal ini, tetapi mereka tidak terlalu terukur. Para ilmuwan dapat menjaga atom dalam keadaan superposisi untuk sementara waktu jika pengaruh lingkungan diminimalkan. Namun, dalam skala yang lebih besar, semuanya, sebagai suatu peraturan, masuk neraka.

Jadi, sementara beberapa orang yang cerdas dalam mantel putih mencari cara untuk menangani dekoherensi, yang lain mencari alat untuk mempelajarinya. Jika Anda ingin mengalahkan musuh Anda, kenalilah dia dengan pandangan, seperti yang mereka katakan.

Sebelum kita terjun ke aliran formula dan penjelasan tentang algoritma yang dikembangkan oleh para ilmuwan, ada baiknya lompatan singkat dalam waktu. Robert Griffiths, seorang ahli fisika Amerika di Universitas Carnegie Mellon, mengusulkan teori sejarah sekuensial (peristiwa) pada tahun 1984: fisika klasik dekat dengan mekanika kuantum, dan matematika kuantum dapat menghitung probabilitas fenomena skala besar dan sub-atomik yang berhubungan bukan dengan hasil pengukuran, tetapi dengan fisik status sistem. Mr. Griffiths memberikan contohnya foto-foto gunung yang dapat diambil dari sudut yang berbeda, dan kemudian membuat gambar gunung yang nyata dari mereka. Dalam kasus fisika kuantum, dimungkinkan untuk memilih parameter pengukuran, tetapi tidak akan bekerja untuk menggabungkan dua pengukuran untuk menyusun gambar lengkap partikel sebelum pengukuran. Sebelum proses aktual mengukur posisi dan momentum nyata, itu tidak ada.


Robert Griffiths

Bingung dan sedikit meniup atap, tapi bukan itu saja. Pada tahun 1989, Murray Gell-Mann dan James Hartl mengemukakan pendapat mereka sendiri berdasarkan teori Griffiths. Menurut pendapat mereka, seluruh Semesta dapat dianggap sebagai sistem kuantum tunggal tanpa lingkungan eksternal. Jika demikian, maka dekoherensi terjadi dalam sistem, dan hasil dari aktivitasnya adalah domain quasiclassical - set sejarah berurutan yang tidak dapat dibedakan dengan latar belakang butiran kasar akibat dekoherensi.

Teori-teori ini membantu memecahkan beberapa masalah dan paradoks dalam mekanika kuantum, tetapi tidak semuanya. Para peneliti percaya bahwa kesimpulan dari pendahulunya ini tidak banyak digunakan karena fakta bahwa perhitungan sistem non-sepele (misalnya, sistem diskrit ukuran yang terlihat atau sistem kontinu yang tidak memungkinkan deskripsi perkiraan dengan integral yang dapat dipecahkan secara tepat) sangat rumit. Dengan kata lain, teori-teori ini baik, tetapi hanya dalam kasus-kasus sederhana.

Dalam beberapa tahun terakhir, pengembangan teknologi kuantum telah sangat dipercepat, dan algoritma hybrid kuantum-klasik variasional ( VHQCA ) telah muncul yang dapat mengatasi dengan baik berbagai tugas (memfaktorkan, mencari kondisi dasar, dll.).

Dalam pekerjaan yang kami pertimbangkan hari ini, para ilmuwan menggambarkan algoritma VHQCA mereka untuk cerita berurutan. Menurut para peneliti, algoritma mereka melampaui metode klasik dalam banyak parameter, termasuk ukuran sistem yang dipelajari.

Maraton rumus (landasan teori)

Kami sudah mengalami penyimpangan sejarah, dan sekarang perlu dibiasakan sedikit dengan dasar komputasi algoritma sebelum mempertimbangkan hasil kerjanya.

Dasar dari sejarah sekuensial (CH) adalah sejarah Y ^α adalah sekuens properti dalam urutan waktu instants t ₁ < t ₂ <... < t _k :



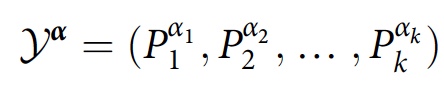
di mana P α j j dipilih dari set proyektor Pj yang dijumlahkan pada waktu tj .

Para ilmuwan memberikan contoh ilustratif: foton melewati beberapa kisi difraksi dan kemudian menabrak layar. Dalam situasi seperti itu, ceritanya mungkin foton melewati satu celah di kisi pertama, celah lain di kedua, dll. Karena itu, ada beberapa gangguan di antara cerita-cerita tersebut. Dan karena ada kendala, mustahil untuk menambahkan secara klasik probabilitas berbagai cerita untuk mengantisipasi prediksi yang tepat tentang titik di mana foton menyentuh layar.

Kerangka kerja CH menyediakan alat untuk menentukan kapan keluarga cerita F = { Y ^α } menunjukkan gangguan, yang tidak selalu jelas. Ini juga mendefinisikan operator kelas:



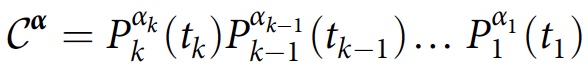
yang merupakan produk yang dipesan berdasarkan waktu dari operator proyeksi dalam sejarah Y ^α . Jika sistem awalnya dijelaskan oleh matriks kerapatan ρ, tingkat gangguan atau tumpang tindih antara sejarah Y ^α dan Y ^{α ′} akan sama dengan:



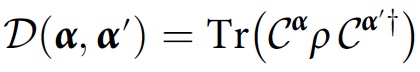
Nilai ini disebut fungsi dekoherensi. Kondisi konsistensi untuk keluarga cerita F dalam hal ini akan terlihat seperti ini:



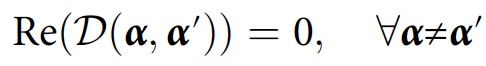
Hanya jika kondisi ini terpenuhi, untuk sejarah Y ^α, probabilitasnya adalah D ( α , α ). Untuk perhitungan yang lebih sederhana, ketentuan lain dapat diterapkan:



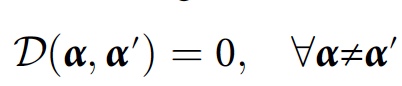
Para ilmuwan mengatakan bahwa untuk algoritme numerik, akan sangat berguna untuk mempertimbangkan perkiraan konsistensi sambil memperhitungkan gangguan minor:



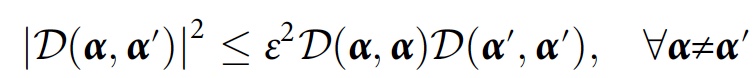
Untuk mempelajari konsistensi yang muncul semata-mata dari dekoherensi (mis., Rekaman di lingkungan), para peneliti mengusulkan metode yang sebagai gantinya mengambil jejak parsial atas E , yang merupakan subsistem lingkungan:



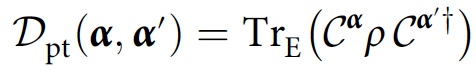
Dengan modifikasi ini, kondisi konsistensi akan terlihat seperti ini:



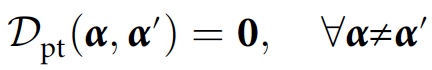
di mana 0 adalah matriks nol. Alih-alih menunjukkan tidak adanya gangguan lingkungan, konsistensi menunjukkan ada / tidaknya kontradiksi dalam catatan cerita di lingkungan.


Gambar No. 1: skema percabangan cerita untuk langkah waktu k.

Mengingat maraton formula dan pemahaman cerita berurutan, para ilmuwan menunjukkan bukti fakta bahwa skema numerik klasik untuk CH tidak mampu mengatasi tugas tersebut.

Gambar di atas menunjukkan contoh di mana ada cerita tentang agregat jumlah partikel n dengan 1/2 putaran untuk langkah waktu k . Jumlah cerita adalah 2 ^nk , oleh karena itu, ada ~ 2 ^{2 nk} elemen fungsional dekoherensi. Selain itu, estimasi setiap elemen fungsional dekoherensi D ( α , α ' ) membutuhkan padanan dari simulasi Hamiltonian sistem, yaitu, perkalian matriks 2 ⁿ x 2 ⁿ . Ini berarti bahwa cluster modern akan membutuhkan ratusan tahun untuk menghitung konsistensi keluarga cerita dengan k = 2 langkah waktu dan n = 10 putaran.

Algoritma VCH Hybrid

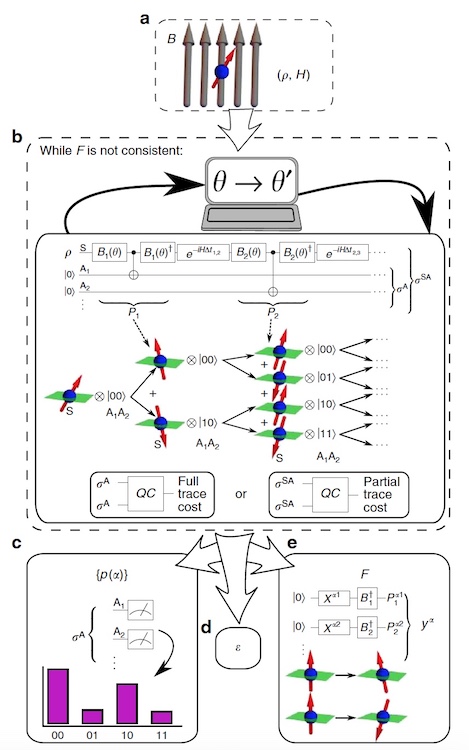Gambar # 2: Diagram blok VCH.

Para ilmuwan menyebut algoritma mereka VHQCA VCH (variabel sekuensial variabel). VCH mengambil input model fisik (mis., Status awal ρ dan Hamiltonian H ) dan beberapa ansatz * untuk jenis proyektor yang perlu dipertimbangkan.

Ansatz * adalah firasat tentang apa solusi persamaan seharusnya dan bentuk apa yang seharusnya.

Data berikut tersedia sebagai data yang dihasilkan:

• keluarga cerita F , yang (kurang-lebih) merupakan jejak lengkap dan / atau sebagian dalam bentuk operator proyeksi yang disiapkan pada komputer kuantum;
• probabilitas cerita yang paling mungkin dari Y ^α di F (maaf untuk permainan kata-kata);
• estimasi parameter konsistensi ε .

VCH mencakup siklus optimisasi parameter di mana komputer kuantum mengevaluasi fungsi biaya yang mengukur ketidakcocokan keluarga, sedangkan pengoptimal klasik menyesuaikan keluarga (mis., Mengubah parameter proyektor) untuk mengurangi biaya.

Untuk menghitung biaya, perlu diperhatikan bahwa unsur-unsur fungsi dekoherensi membentuk matriks semidefinit positif. Properti ini digunakan dalam VCH untuk menyandikan D dalam keadaan kuantum σ ^A , elemen matriksnya adalah ⟨α | σ ^A | α ′ ⟩ = D ( α , α ′ ).

2b menunjukkan sirkuit kuantum yang menyiapkan σ ^A dengan mengubah keadaan awal ρ ⊗ | 0〉 〈0 | dalam sistem SA (di mana S memodelkan sistem fisik yang menarik dan A adalah sistem tambahan) ke keadaan σ ^SA , nilai batasnya adalah σ ^A.

Untuk konsistensi jejak penuh dari matriks, ukuran global konsistensi diperkenalkan, yang secara kuantitatif menentukan seberapa jauh σ ^A dari diagonal, yang berfungsi sebagai fungsi biaya:



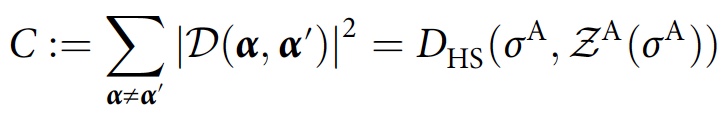
di mana D _HS adalah jarak Hilbert-Schmidt dan Z ^A ( σ ^A ) adalah fase (semua elemen off-diagonal diatur ke nol) versi σ ^A.

Kuantitas ini cenderung nol jika dan hanya jika F konsisten. Untuk kasus jejak parsial, fungsi biaya serupa diperoleh, tetapi dengan σ ^A digantikan oleh σ ^SA :



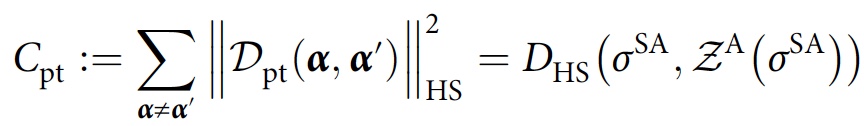
Siklus optimisasi parameter mengarah ke sekumpulan cerita F yang konsisten, di mana parameter konsistensi ε dibatasi dari atas sebagai bagian dari biaya akhir.

2c menunjukkan generasi probabilitas untuk cerita yang paling mungkin dengan berulang kali menyiapkan σA dan mengukur pada basis standar, di mana frekuensi pengukuran memberikan probabilitas.

2e menunjukkan bagaimana menyiapkan seperangkat operator proyeksi untuk setiap sejarah yang diberikan dalam F.

Hasil Eksperimen

Beberapa percobaan berbeda menggunakan algoritma VCH dilakukan. Kami akan mempertimbangkan dua - putaran dalam medan magnet dan molekul kiral.

Putar dalam medan magnet

Gambar No. 3

Dalam percobaan pertama, kami mempertimbangkan dua sejarah waktu suatu partikel dengan spin 1/2 di medan magnet Bz , yang Hamiltoniannya adalah H = - γBσ _z . Cerita-cerita yang kami pertimbangkan memiliki langkah waktu antara keadaan awal dan proyektor pertama, dan juga antara proyektor pertama dan kedua. Selain itu, perlu dicatat bahwa hanya proyektor pada bidang xy dari bola Bloch yang dipertimbangkan.

Gambar di atas menunjukkan grafik biaya untuk prosesor kuantum ibmqx5, serta untuk simulator, yang akurasinya dibatasi dengan cara melapis statistik final yang sama yang dikumpulkan menggunakan prosesor kuantum. Beberapa posisi terendah ditemukan ketika menjalankan VCH pada ibmqx5 tumpang tindih diagram. Karena minimum ini sesuai dengan keluarga yang secara teoritis konsisten, ini mewakili keberhasilan VCH dalam praktiknya.

Molekul kiral

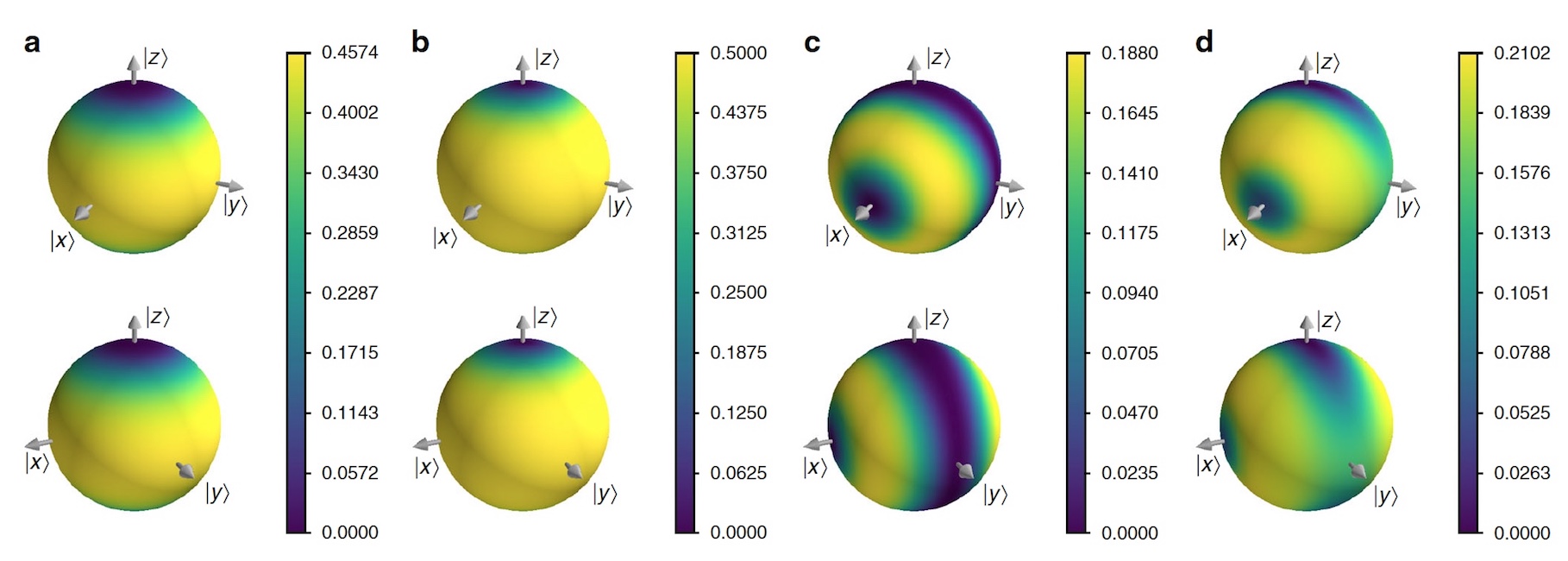Gambar No. 4

Molekul kiral dipilih untuk percobaan praktis, karena ini adalah cara terbaik untuk menentukan penerapan VCH. Molekul kiral dimodelkan sebagai sistem dua tingkat di mana status kiralitas | R〉 dan kiri | L〉 digambarkan sebagai | R⟩ / | L⟩ = | +⟩ / | -⟩ = 1 / √2 * (| 0⟩ ± | 1⟩).

Terowongan molekul kiral yang terisolasi antara | R⟩ dan | L⟩, tetapi para ilmuwan berspekulasi bahwa itu ada dalam gas, di mana tabrakan dengan molekul lain mentransmisikan informasi tentang kiralitas molekul ke lingkungannya. Transfer informasi ini dimodelkan dengan rotasi melalui sudut θ _{x di} sekitar sumbu x dari qubit medium yang dikendalikan oleh chirality sistem.

Para ilmuwan kemudian mempertimbangkan keluarga sederhana dari sejarah stasioner, di mana satu set proyektor sesuai dengan basis yang sama semua lima kali (untuk kesederhanaan pemodelan, ditemukan bahwa molekul bertabrakan dengan molekul lain 5 kali). Dengan asumsi θ _z adalah sudut presesi karena tunneling waktu antara tabrakan, maka dimungkinkan untuk menyelidiki persaingan antara dekoherensi dan tunneling. Gambar di atas menunjukkan hasil simulasi ini.

Para ilmuwan mencatat fakta yang aneh - ada transisi dari rezim kuantum, di mana chirality tidak berurutan, ke rezim klasik, di mana chirality bersifat berurutan dan stabil dari waktu ke waktu.

Untuk seorang kenalan yang lebih mendetail dengan nuansa penelitian ini, saya sarankan Anda melihat laporan para ilmuwan dan bahan tambahan untuk itu.

Epilog

Karya ini mendemonstrasikan algoritma baru, yang, dalam hubungannya dengan komputer kuantum yang ada dan yang akan datang, dapat menggambarkan proses rumit dan membingungkan seperti transisi kuantum-klasik. Studi tentang fenomena ini sangat penting jika kita ingin membuat komputer kuantum yang nyata, berfungsi dan efisien, yang operasinya tidak akan terpengaruh oleh dekoherensi.

Algoritma VCH berada pada tahap awal pengembangan, tetapi sudah menunjukkan kinerjanya. Di masa depan, para ilmuwan bermaksud, secara alami, untuk memperbaikinya. Meskipun demikian, prospek penerapan awal komputasi kuantum tidak hanya tetap pada tingkat yang sama, tetapi tumbuh dengan setiap studi tersebut.

Terima kasih atas perhatian Anda, tetap penasaran, dan selamat bekerja, kawan! :)

Terima kasih telah tinggal bersama kami. Apakah Anda suka artikel kami? Ingin melihat materi yang lebih menarik? Dukung kami dengan melakukan pemesanan atau merekomendasikannya kepada teman-teman Anda, diskon 30% untuk pengguna Habr pada analog unik dari server entry-level yang kami temukan untuk Anda: Seluruh kebenaran tentang VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps dari $ 20 atau bagaimana membagi server? (opsi tersedia dengan RAID1 dan RAID10, hingga 24 core dan hingga 40GB DDR4).

Dell R730xd 2 kali lebih murah? Hanya kami yang memiliki 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV dari $ 199 di Belanda! Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - mulai dari $ 99! Baca tentang Cara Membangun Infrastruktur Bldg. kelas menggunakan server Dell R730xd E5-2650 v4 seharga 9.000 euro untuk satu sen?