Kebisingan putih menarik kotak hitam. Bagian 2. Solusi

Dalam publikasi pertama , dikatakan bahwa ada teorema Erd-s-Renyi yang terlupakan, dari mana ia mengikuti bahwa dalam serangkaian acak panjang N, dengan probabilitas mendekati 1, terdapat deretan nilai panjang identik yang panjang. $$$\ log_2 {N}$. Properti yang ditunjukkan dari variabel acak dapat digunakan untuk menjawab pertanyaan: "Setelah memproses data besar, apakah seri residu mematuhi hukum angka acak atau tidak?"

Jawaban atas pertanyaan ini ditentukan bukan atas dasar uji korespondensi dengan normalitas distribusi, tetapi atas dasar sifat-sifat rangkaian residu itu sendiri.

Dengan ada atau tidak adanya atau pergeseran frekuensi kontrak dari karakter yang sama. Saya mencoba untuk menerbitkan, untuk menunjukkan kemungkinan menggunakan alat ini, meskipun banyak pertanyaan muncul tentang bagaimana ini bekerja dalam kenyataan ketika melakukan analisis dalam data besar. Tetapi diskusi itu produktif, dan pengguna VDG bahkan memberikan contoh nyata: "... Cabang dendritik neuron dapat direpresentasikan sebagai sedikit urutan. Cabang, dan kemudian seluruh neuron, dipicu ketika rantai sinapsis diaktifkan di salah satu tempatnya. Neuron memiliki tugas untuk tidak menanggapi white noise, masing-masing, panjang minimum rantai, sejauh yang saya ingat di Numenta, adalah 14 sinapsis dalam neuron piramidal dengan 10 ribu sinapsisnya. Dan menurut rumus kita dapatkan: $\ log_2 {10000} = $ 13.28$. Artinya, rantai yang panjangnya kurang dari 14 akan terjadi karena kebisingan alami, tetapi tidak akan mengaktifkan neuron. Benar-benar sempurna . "

Mari kita coba mempertimbangkan mekanisme yang disajikan dalam materi ini.

Publikasi pertama menimbulkan banyak pertanyaan. Mari kita coba memperjelas mekanisme teorema Erds-Renyi dalam artikel ini.

Solusi muncul sehubungan dengan paradoks Penny Game . Permainan terdiri dari yang berikut - dua pemain A dan B akan melempar koin lima kali, menugaskan, misalnya, "elang" - 1, "ekor" - 0. Pemain A memilih urutan tiga nilai dan menyuarakannya, misalkan 001.

Pemain B memilih urutannya, misalkan 100. Pemain yang urutannya jatuh lebih dulu adalah pemenang. Misalkan 01001 telah jatuh, yaitu 0-100-1, yang sesuai dengan pilihan B. Paradoks dari “Permainan Penny” adalah bahwa tidak peduli urutan pemain yang dipilih A, pemain B selalu memiliki kesempatan untuk memilih urutan, probabilitas yang lebih besar dari urutan yang dipilih oleh pemain A. Matriks pemenang pemain B ditunjukkan pada Gambar 1.


Fig. 1. Matriks hasil untuk pemain B di "Penny Game" untuk lima tembakan.

Efek dari paradoks ini adalah bahwa rangkaian acak tidak transitif, yaitu, jika U> R, dan R> Q, maka ini tidak berarti bahwa Q> U.

Konsekuensi dari paradoks ini adalah hal-hal biasa berikut, jika seorang pemain bermain dengan aturan dan mematuhi hukum teori probabilitas:

1. Dalam judi, ia biasanya menang, yang kasirnya lebih - “hancurkan bank”.
2. Di kasino, hanya kasino yang menang.
3. Saat bermain di bursa saham, hanya keberuntungan yang menentukan berapa lama seorang trader akan bertahan sampai ia kehilangan modalnya.

Arti fisik hukum ini, yang menjadi dasar paradoks "Penny Game", adalah bahwa orang yang dapat melanjutkan urutan acak lebih memiliki keunggulan. Seperti dalam contoh pertama - pemain yang memiliki lebih banyak uang. Pada opsi kedua - kasino bermain dengan ratusan urutan pada saat yang sama, dan akan terus bermain setelah salah satu pemain menghentikan permainan. Sebuah permainan melawan pertukaran satu pemain tidak bisa dibandingkan, dengan jutaan operasi di bursa.

Seperti yang Anda lihat, undang-undang pertama dibuat - BigData menentukan situasi dibandingkan dengan informasi lokal.

Momen penentu kedua adalah tidak adanya properti transitivitas dari urutan acak. Konsekuensi dari ini adalah ketidakmampuan untuk memutar balik situasi.

Hipotesis lebih lanjut dalam analisis BigData:

1) Pemahaman tentang pengembangan acara hanya dimungkinkan pada volume seperti itu di mana konsekuensi dari peristiwa yang diselidiki dicatat. Mekanisme untuk proses ini dapat direpresentasikan sebagai berikut. Bidang acak adalah bidang di mana beberapa proses potensial berusaha untuk mewujudkan diri. Setelah realisasi diri, proses meninggalkan perubahan, dan kami mencoba mendeteksi tingkat jejak dari proses yang telah terjadi. Ketergantungan sudah ditentukan oleh besarnya pembagian hasil kiri. Saya akan menjelaskan kepada yang di atas bahwa, menurut pendapat saya, cara transformasi itu sendiri terjadi, pada saat ini, sains tidak dapat memberikan definisi formal. Jika definisi-definisi ini benar, maka beberapa paradoks Zeno akan berhenti menjadi paradoks, dan kesatuan dan perjuangan lawan, dialektika materialis akan berhenti menjadi postulat di dalamnya.

Saya kira tidak ada gunanya mematahkan tombak pernyataan bahwa jika kita menentukan proses setelah fakta, maka ini adalah latihan yang tidak berarti, karena proses selanjutnya tidak dapat diprediksi. Seseorang melihat secara lokal, dan proses BigData dapat berlangsung milyaran tahun, jadi kami memiliki kesempatan untuk melihat mekanisme proses dari bidang BigData. Materi menarik tentang nilai-nilai besar alam semesta disajikan di sini .

2) Hipotesis kedua, yang dapat disimpulkan dari tidak adanya sifat transitivitas, adalah pengaruh interval dan kondisi pada proses yang diteliti. Yaitu, di satu sisi, ada waktu koordinat yang memposisikan proses yang sedang dipelajari, dan kesempatan untuk mengulangi kondisi di mana proses kami dibentuk, dan jutaan catatan diterima, hampir mustahil. Di sisi lain, hukum kombinatorik tidak dapat diabaikan. Undang-undang ini memberi tahu kita bahwa kemungkinan terjadinya kombinasi tertentu harus selalu ada. Gambar 2 menunjukkan distribusi varian rantai sinyal N di mana ada deretan sub-order panjang k. Jumlah total lebih besar dari $$$2 ^ N$, karena rantai pendek digabungkan dengan yang lebih panjang.


Fig. 2. Jumlah varian sub-order yang mungkin dari sinyal identik k, dalam urutan nilai N.

Untuk varian di mana rantai lebih panjang dari N / 2 hadir, mereka diisi dengan warna kuning, jumlah mereka ditentukan dengan cara yang cukup sederhana dengan rumus:



Artinya, probabilitas yang sesuai untuk seri yang berisi rantai k> = N / 2 nilai identik (kami tidak akan menggambarkan probabilitas serangkaian nilai N) akan ditentukan oleh rumus:



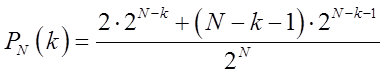
Selama diskusi, pada bagian pertama, muncul pertanyaan, esensi yang diringkas menjadi berikut: "Di mana batas-batas white noise?" Di sini, mengingat tabel Gambar 2, hipotesis dibentuk untuk diskusi, sesuai dengan skema berikut.

Berdasarkan teorema integral Muavre-Laplace:



Kami mendefinisikan interval untuk f (1,96) = probabilitas 95%:



Jika Anda melihat, tabel pada Gambar 2 mencerminkan bidang penuh probabilitas, di sisi lain, parameter distribusi dalam setiap kasus dapat didefinisikan secara unik, dan disajikan pada Gambar 3, di mana kami menunjukkannya sebagai contoh dari serangkaian nilai 9. Karena banyaknya opsi $$$2 ^ 9 {= 512}$, dan untuk jumlah tes ini kita akan menemukan alpha.


Fig. 3. Batas-batas interval probabilitas sub-order panjang k dari sinyal yang sama, dalam urutan 9 nilai, dengan keandalan 2 sigma (95%).

Gambar 4 menyajikan interval untuk variabel acak, di mana Gambar 4b adalah Gambar 4a yang ditransformasikan.


Fig. 4. Interval ukuran acak untuk setiap subordo, dengan keandalan 95%.

Untuk menyusun jawaban atas pertanyaan di mana white noise berada, ia merumuskan pendekatan yang ada sebagai berikut:

1. Kebisingan putih diakui oleh masyarakat;
2. Data yang dapat dirumuskan dengan ekspresi analitis;
3. Informasi terstruktur oleh jaringan saraf;
4. Qubit, komputer kuantum;
5. BigData
6. Jika data besar ada, maka sangat mungkin bahwa hyperdata ada.

Untuk penataan yang diusulkan, petunjuknya adalah ide O. V. Filatov “Definisi urutan biner acak sebagai objek kombinatorial. Perhitungan potongan-potongan yang bersamaan dalam urutan biner acak ” tentang perilaku fragmen dari urutan yang menyerupai perilaku partikel di microworld.

Qubit, yang memiliki struktur tiga dimensi, memberi alasan untuk percaya bahwa skema struktural harus memiliki model tiga dimensi. Beberapa lapisan, yang diakui oleh masyarakat, menyiratkan pelapisan model dan, menggabungkan semua ini, skema yang paling elegan adalah mungkin dalam bentuk toroid, Gambar 5.


Fig. 5. Asumsi struktur data dalam pemetaan variabel acak ke ruang (gambar diambil dari Internet).

Mengembangkan alasan lebih lanjut, kami mencatat bahwa pada Gambar 3, semua frekuensi adalah bilangan genap. Ini adalah konsekuensi dari simetri data "0-1". Simetri data acak tercermin dalam Postulat of Golomb karya Solomon Wolf Golomb . Berdasarkan penelitian Filatova O.V. “Penurunan formula untuk postulat Golomb. Cara untuk membuat urutan pseudo-acak dari frekuensi Mises. Dasar-dasar "Combinatorics of Long Sequences" menggunakan konsep setengah gelombang. Saya percaya bahwa aspek ini penting dalam studi white noise, karena dikaitkan dengan parameter seperti panjang baris.

Mengingat sifat-sifat proses acak, gelombang white noise dapat memperoleh berbagai properti, termasuk kurangnya simetri gelombang dan kemungkinan ketidakpatuhan dengan teorema Noether . Tetapi ada proses di dunia fisik seperti pembentukan busa dari gelombang selancar, Gambar 6. Jadi, kita memiliki setiap alasan untuk memungkinkan parameter yang tidak biasa dari gelombang derau putih.


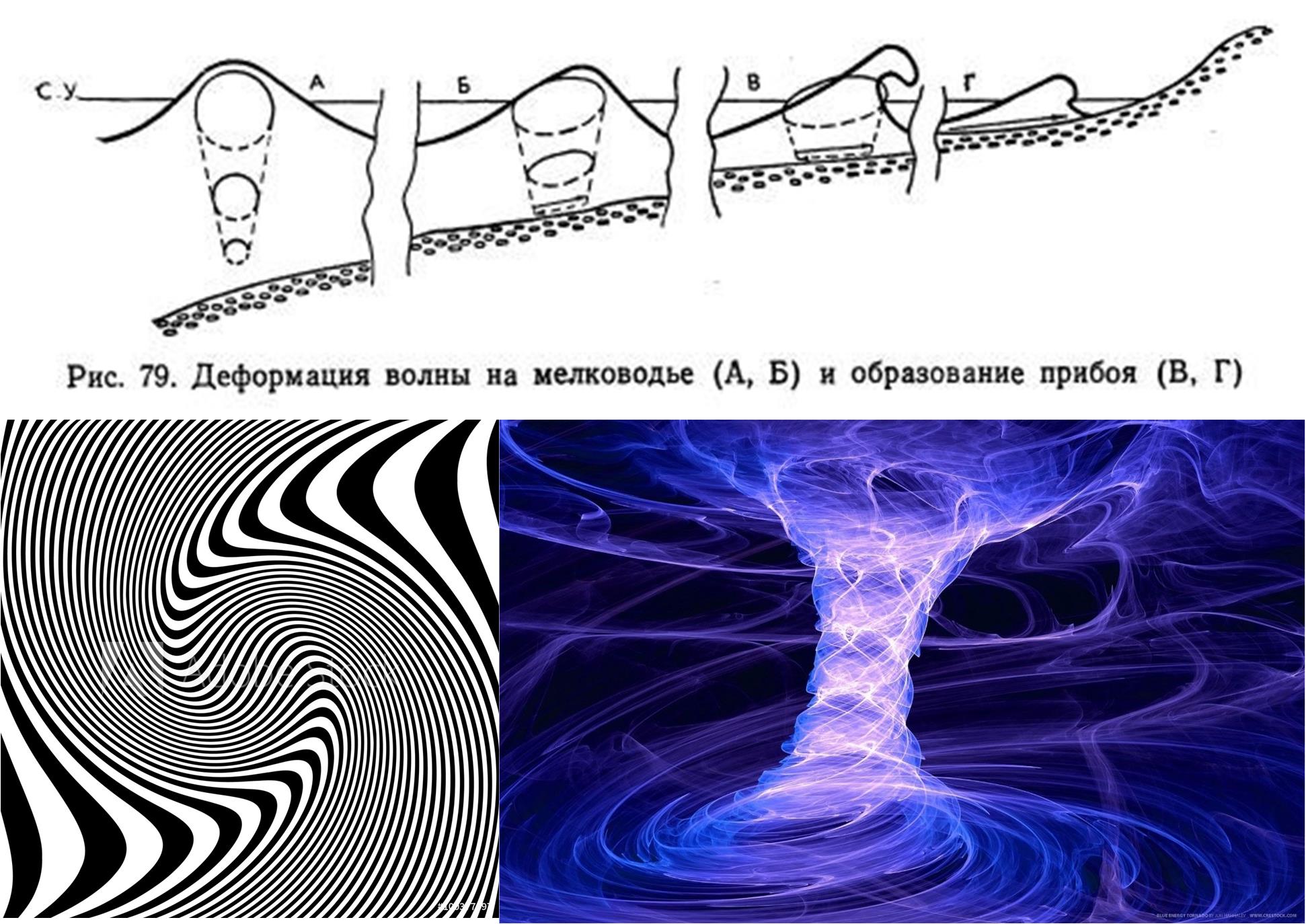Fig. 6. Mekanisme deformasi gelombang dekat pantai dan contoh-contoh proses yang, ketika diproyeksikan ke beberapa pesawat terbang, di ruang lokal, mungkin terlihat seperti proses acak (gambar diambil dari Internet).

Beralih ke bagian praktis, saya akan meringkas pendekatan yang diusulkan ketika bekerja dengan white noise.

1. Kurangnya sifat transitivitas dalam proses acak.
2. Asumsi bahwa properti simetri dalam white noise adalah realisasi dari properti simetri dari proses yang lebih tinggi dari proses dalam situasi saat ini yang dipertimbangkan.
3. Lokalitas proses acak. Premis ini tidak secara eksplisit ditampilkan dalam publikasi, tetapi cukup cocok dalam kerangka matematika konstruktif. Anda semua menggunakannya (matematika konstruktif) ketika Anda menulis skrip yang menetapkan persyaratan untuk mengakses sel memori dan membaca isinya. Karena secara default Anda berarti bahwa dalam sel ini ada nilai 0 atau 1 dan tidak ada lagi yang bisa ada di sana. Materi yang baik untuk membiasakan diri dengan pendekatannya disajikan di sini: N.N. Nepeyvoda "Konstruktif matematika: ulasan prestasi, kelemahan dan pelajaran. Bagian I " .

Bagian praktis

Pada bagian pertama, pertanyaan teorema Erd-Renyi diperiksa, yang terdiri dari fakta bahwa teorema ini hanya ditemukan dalam satu sumber, yang diterjemahkan dari bahasa Hongaria, buku ini diterbitkan kembali di Uni Soviet dan tidak ada bukti atau penyebutan ditemukan. . Sebagai konsekuensi dari fakta ini, ada ketidakpastian secara umum tentang keberadaannya dan, terlebih lagi, penerapannya.

Sebagai hasil pencarian, ditemukan dalam karya Filatov O.V. “Penurunan formula untuk postulat Golomb. Cara untuk membuat urutan pseudo-acak dari frekuensi Mises. Dasar-dasar "Combinatorics of long sequence" hal 15 berikut ini, Gambar 7, saya mengutip yang asli dari materi.


Fig. 7. Bagian asli dari publikasi Filatova OV “Penurunan formula untuk postulat Golomb. Cara untuk membuat urutan pseudo-acak dari frekuensi Mises. Dasar-dasar "Kombinatorik urutan panjang."

Teorema Erds-Renyi dirumuskan sebagai berikut:

Saat melempar koin sebanyak N kali, serangkaian sisi koin jatuh dengan panjang yang sama $$$\ log_2 {N}$diamati dengan probabilitas cenderung 1, dengan N cenderung tak terhingga.
Kami menulis teorema dalam formulasi “Combinatorics of long sequence” untuk satu sisi mata uang:



Kami melakukan buktinya:



Seperti Anda dapat melihat frekuensi Mises untuk kereta yang terdiri dari rantai sinyal identik panjang $$$n = \ log_2 {N}$bertepatan dengan kesimpulan teorema Erdos-Renyi pada probabilitas rantai yang sama dalam kasus seri acak. Sehingga Anda bisa menghilangkan keraguan dan mengenali keberadaannya serta kemungkinan aplikasi.

Karena publikasi sudah lebih direkomendasikan oleh pemasar, kelanjutan di bagian selanjutnya, “White noise menarik kotak hitam. Bagian 3. Aplikasi. "

Bagian lain: Bagian 1 , Bagian 3 .