Jaringan saraf dan pembelajaran mendalam: tutorial online, bab 6, bagian 1: pembelajaran mendalam

Dalam bab terakhir, kami belajar bahwa deep neural networks (GNSs) seringkali lebih sulit untuk dilatih daripada yang dangkal. Dan ini buruk, karena kami punya banyak alasan untuk percaya bahwa jika kami bisa melatih STS, mereka akan jauh lebih baik dalam melakukan tugas. Tetapi sementara berita dari bab sebelumnya mengecewakan, itu tidak akan menghentikan kita. Dalam bab ini, kita akan mengembangkan teknik yang dapat kita gunakan untuk melatih jaringan yang dalam dan mempraktikkannya. Kami juga akan melihat situasi yang lebih luas, secara singkat berkenalan dengan kemajuan terbaru dalam penggunaan GNS untuk pengenalan gambar, ucapan dan untuk aplikasi lain. Dan juga secara dangkal mempertimbangkan masa depan jaringan saraf dan AI yang bisa diharapkan.

Ini akan menjadi bab yang panjang, jadi mari kita sedikit membahas daftar isi. Bagian-bagiannya tidak saling berhubungan kuat, oleh karena itu, jika Anda memiliki beberapa konsep dasar tentang jaringan saraf, Anda bisa mulai dengan bagian yang lebih menarik bagi Anda.

Bagian utama dari bab ini adalah pengantar untuk salah satu jenis jaringan yang paling populer: jaringan konvolusi yang dalam (GSS). Kami akan bekerja dengan contoh terperinci penggunaan jaringan konvolusi, dengan kode dan hal-hal lain, untuk memecahkan masalah pengelompokan digit tulisan tangan dari set data MNIST:



Kami memulai ulasan kami tentang jaringan konvolusional dengan jaringan dangkal, yang kami gunakan untuk menyelesaikan masalah ini sebelumnya dalam buku ini. Dalam beberapa tahap kita akan menciptakan jaringan yang lebih kuat. Sepanjang jalan, kita akan mengenal banyak teknologi canggih: convolutions, pooling, menggunakan GPU untuk secara serius meningkatkan jumlah pelatihan dibandingkan dengan apa yang kita lakukan dengan jaringan dangkal, ekspansi algoritmik data pelatihan (untuk mengurangi overfitting), menggunakan teknologi putus sekolah (juga untuk mengurangi pelatihan ulang), menggunakan ansambel jaringan, dan lainnya. Akibatnya, kita akan sampai pada sistem yang kemampuannya hampir di tingkat manusia. Dari 10.000 gambar verifikasi MNIST - yang tidak dilihat oleh sistem selama pelatihan - akan dapat mengenali 9967 dengan benar. Dan berikut adalah beberapa gambar yang tidak dikenali dengan benar. Di sudut kanan atas adalah opsi yang benar; apa yang ditunjukkan oleh program kami ditunjukkan di sudut kanan bawah.



Banyak dari mereka yang sulit untuk diklasifikasikan ke manusia. Ambil, misalnya, digit ketiga di baris atas. Menurut saya lebih seperti "9" daripada versi resmi "8". Jaringan kami juga memutuskan bahwa itu "9". Setidaknya, kesalahan semacam itu dapat dipahami sepenuhnya, dan bahkan mungkin disetujui. Kami menyimpulkan diskusi kami tentang pengenalan gambar dengan ikhtisar kemajuan luar biasa yang baru-baru ini dicapai oleh jaringan saraf (khususnya, yang konvolusional).

Sisa bab ini dikhususkan untuk diskusi pembelajaran mendalam dari sudut pandang yang lebih luas dan kurang rinci. Kami akan mempertimbangkan secara singkat model NS lainnya, khususnya, NS berulang, dan unit memori jangka pendek jangka panjang, dan bagaimana model ini dapat digunakan untuk menyelesaikan masalah dalam pengenalan suara, pemrosesan bahasa alami, dan lainnya. Kami akan membahas masa depan NS dan pertahanan sipil, dari ide-ide seperti antarmuka pengguna yang digerakkan oleh niat untuk peran pembelajaran yang mendalam di AI.

Bab ini didasarkan pada bahan dari bab-bab sebelumnya buku ini, menggunakan dan mengintegrasikan ide-ide seperti backpropagation, regularisasi, softmax, dan sebagainya. Namun, untuk membaca bab ini tidak perlu menguraikan materi dari semua bab sebelumnya. Namun, tidak ada salahnya membaca Bab 1 , dan mempelajari tentang dasar-dasar Majelis Nasional. Ketika saya menggunakan konsep-konsep dari Bab 2 hingga 5, saya akan memberikan tautan yang diperlukan ke materi yang diperlukan.

Perlu dicatat bahwa bab ini tidak. Ini bukan materi pelatihan tentang perpustakaan terbaru dan paling keren untuk bekerja dengan NS. Kami tidak akan melatih STS dengan lusinan lapisan untuk menyelesaikan masalah dari ujung tombak penelitian. Kami akan mencoba memahami beberapa prinsip dasar yang mendasari GNS dan menerapkannya pada konteks tugas MNIST yang sederhana dan mudah dipahami. Dengan kata lain, bab ini tidak akan membawa Anda ke garis depan wilayah ini. Keinginan ini dan bab-bab sebelumnya adalah berkonsentrasi pada dasar-dasar, dan mempersiapkan Anda untuk memahami berbagai karya kontemporer.

Pengantar jaringan saraf convolutional

Dalam bab-bab sebelumnya, kami mengajarkan jaringan saraf kami bahwa cukup baik untuk mengenali gambar angka tulisan tangan:



Kami melakukan ini menggunakan jaringan di mana lapisan tetangga saling terhubung satu sama lain. Artinya, setiap neuron jaringan dikaitkan dengan masing-masing neuron dari lapisan tetangga:



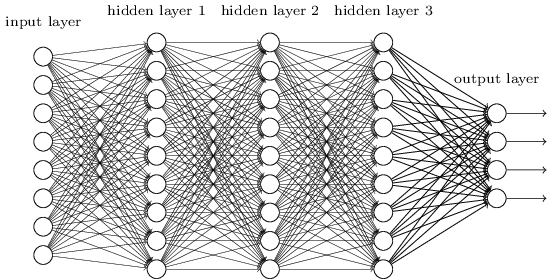
Secara khusus, kami mengkodekan intensitas setiap piksel dalam gambar sebagai nilai untuk neuron yang sesuai dari lapisan input. Untuk gambar berukuran 28x28 piksel, ini berarti bahwa jaringan akan memiliki 784 (= 28 × 28) neuron yang masuk. Kemudian kami melatih bobot dan offset jaringan sehingga keluaran jaringan (ada harapan seperti itu) dengan benar mengidentifikasi gambar yang masuk: '0', '1', '2', ..., '8', atau '9'.

Jaringan awal kami bekerja dengan sangat baik: kami mencapai akurasi klasifikasi di atas 98% menggunakan data pelatihan dan pengujian dari angka tulisan tangan MNIST. Tetapi jika Anda mengevaluasi situasi ini sekarang, rasanya aneh menggunakan jaringan dengan lapisan yang terhubung penuh untuk mengklasifikasikan gambar. Faktanya adalah bahwa jaringan seperti itu tidak memperhitungkan struktur spasial gambar. Misalnya, ini berlaku persis sama dengan piksel yang terletak jauh dari satu sama lain, serta piksel yang berdekatan. Diasumsikan bahwa kesimpulan tentang konsep-konsep struktur ruang seperti itu harus dibuat berdasarkan studi data pelatihan. Tetapi bagaimana jika, alih-alih memulai struktur jaringan dari awal, kita akan menggunakan arsitektur yang mencoba mengambil keuntungan dari struktur spasial? Pada bagian ini, saya menggambarkan jaringan saraf convolutional (SNA). Mereka menggunakan arsitektur khusus, terutama cocok untuk mengklasifikasikan gambar. Melalui penggunaan arsitektur seperti itu, SNA belajar lebih cepat. Dan ini membantu kami melatih jaringan yang lebih dalam dan lebih berlapis yang melakukan pekerjaan yang baik dalam mengklasifikasikan gambar. Saat ini, SNA dalam atau beberapa varian serupa digunakan dalam sebagian besar kasus pengenalan gambar.

Asal usul SNA kembali ke tahun 1970-an. Tetapi karya awal, yang memulai distribusi modern mereka, adalah karya tahun 1998, " Gradient Learning for Recognizing Documents ." Lekun membuat komentar menarik tentang terminologi yang digunakan dalam SNA: "Koneksi model seperti jaringan konvolusional dengan neurobiologi sangat dangkal. Oleh karena itu, saya menyebutnya jaringan konvolusional, bukan jaringan saraf convolutional, dan oleh karena itu kami menyebut elemen node mereka, bukan neuron. " Namun, meskipun demikian, SNA menggunakan banyak ide dari dunia NS yang telah kita pelajari: propagasi balik, gradient descent, regularisasi, fungsi aktivasi nonlinier, dll. Oleh karena itu, kami akan mengikuti perjanjian yang diterima secara umum dan menganggap mereka semacam NA. Saya akan memanggil mereka baik jaringan dan jaringan saraf, dan simpul mereka - baik neuron maupun elemen.

SNA menggunakan tiga ide dasar: bidang reseptif lokal, bobot total, dan pengumpulan. Mari kita lihat ide-ide ini secara bergantian.

Bidang penerimaan lokal

Dalam lapisan jaringan yang terhubung penuh, lapisan input ditunjukkan oleh garis vertikal neuron. Dalam SNA, akan lebih mudah untuk mewakili lapisan input dalam bentuk kuadrat neuron dengan dimensi 28x28, nilai-nilai yang sesuai dengan intensitas piksel gambar 28x28:



Seperti biasa, kami mengaitkan piksel yang masuk dengan lapisan neuron tersembunyi. Namun, kami tidak akan mengaitkan setiap piksel dengan setiap neuron tersembunyi. Kami mengatur komunikasi di area kecil yang dilokalkan dari gambar yang masuk.

Lebih tepatnya, setiap neuron dari lapisan tersembunyi pertama akan dikaitkan dengan sebagian kecil dari neuron yang masuk, misalnya, wilayah 5x5 sesuai dengan 25 piksel yang masuk. Jadi, untuk beberapa neuron tersembunyi, hubungannya mungkin terlihat seperti ini:



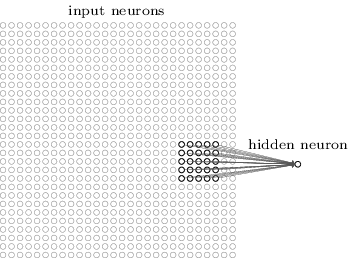
Bagian gambar yang masuk ini disebut bidang reseptif lokal untuk neuron tersembunyi ini. Ini adalah jendela kecil yang melihat piksel yang masuk. Setiap ikatan mempelajari bobotnya. Juga, neuron yang tersembunyi mempelajari perpindahan umum. Kita dapat mengasumsikan bahwa neuron khusus ini sedang belajar menganalisis bidang reseptif lokal spesifiknya.

Lalu kami memindahkan bidang penerimaan lokal ke seluruh gambar yang masuk. Setiap bidang reseptif lokal memiliki neuron tersembunyi di lapisan tersembunyi pertama. Untuk ilustrasi yang lebih spesifik, mulailah dengan bidang penerimaan lokal di sudut kiri atas:



Pindahkan bidang penerimaan lokal satu piksel ke kanan (satu neuron) untuk mengaitkannya dengan neuron tersembunyi kedua:



Jadi kita membangun lapisan tersembunyi pertama. Perhatikan bahwa jika gambar yang masuk adalah 28x28 dan bidang penerima lokal 5x5, maka akan ada 24x24 neuron di lapisan tersembunyi. Ini karena kita hanya bisa menggerakkan bidang reseptif lokal oleh 23 neuron ke kanan (atau ke bawah), dan kemudian kita akan menemukan sisi kanan (atau bawah) dari gambar yang masuk.

Dalam contoh ini, bidang penerimaan lokal bergerak satu piksel pada satu waktu. Namun terkadang ukuran langkah yang berbeda digunakan. Misalnya, kita dapat menggeser bidang penerima lokal 2 piksel ke samping, dan dalam hal ini kita dapat berbicara tentang ukuran langkah 2. Dalam bab ini kita terutama akan menggunakan langkah 1, tetapi Anda harus tahu bahwa kadang-kadang percobaan dengan langkah-langkah dari ukuran yang berbeda dilakukan . Anda dapat bereksperimen dengan ukuran langkah, seperti dengan hiperparameter lainnya. Anda juga dapat mengubah ukuran bidang penerimaan lokal, tetapi biasanya ternyata ukuran yang lebih besar dari bidang penerimaan lokal berfungsi lebih baik pada gambar yang secara signifikan lebih besar dari 28x28 piksel.

Total bobot dan offset

Saya menyebutkan bahwa setiap neuron tersembunyi memiliki bobot offset dan 5x5 yang terkait dengan bidang reseptif lokalnya. Tapi saya tidak menyebutkan bahwa kita akan menggunakan bobot dan perpindahan yang sama untuk semua neuron tersembunyi 24x24. Dengan kata lain, untuk neuron j tersembunyi, k, hasilnya akan sama dengan:

$$

$$\ sigma \ kiri (b + \ sum_ {l = 0} ^ 4 \ sum_ {m = 0} ^ 4 w_ {l, m} a_ {j + l, k + m} \ kanan) \ tag {125}$$

Di sini σ adalah fungsi aktivasi, mungkin sigmoid dari bab-bab sebelumnya. b adalah nilai total offset. w _{l, m} - array dari total bobot 5x5. Dan akhirnya, a _{x, y} menunjukkan aktivasi input pada posisi x, y.

Ini berarti bahwa semua neuron di lapisan tersembunyi pertama mendeteksi tanda yang sama, hanya terletak di bagian gambar yang berbeda. Tanda yang terdeteksi oleh neuron tersembunyi adalah urutan masuk tertentu yang mengarah ke aktivasi neuron: mungkin tepi gambar, atau beberapa bentuk. Untuk memahami mengapa ini masuk akal, anggaplah bobot dan perpindahan kita sedemikian rupa sehingga neuron tersembunyi dapat mengenali, katakanlah, wajah vertikal dalam bidang reseptif lokal tertentu. Kemampuan ini mungkin berguna di tempat lain dalam gambar. Oleh karena itu, berguna untuk menggunakan pendeteksi fitur yang sama di seluruh area gambar. Secara lebih abstrak, SNA disesuaikan dengan baik dengan invarian translasi gambar: memindahkan gambar, misalnya, kucing, sedikit ke samping, dan masih akan tetap menjadi gambar kucing. Benar, gambar dari masalah klasifikasi digit MNIST semuanya terpusat dan dalam ukuran dinormalisasi. Oleh karena itu, MNIST memiliki lebih sedikit invarian translasi daripada gambar acak. Namun, fitur seperti wajah dan sudut cenderung berguna di seluruh permukaan gambar yang masuk.

Untuk alasan ini, kadang-kadang kita merujuk pada pemetaan lapisan yang masuk dan lapisan tersembunyi sebagai peta fitur. Bobot yang menentukan peta karakteristik, kami sebut bobot total. Dan bias mendefinisikan peta fitur adalah bias umum. Sering dikatakan bahwa bobot total dan perpindahan menentukan kernel atau filter. Tetapi dalam literatur orang kadang menggunakan istilah ini untuk alasan yang sedikit berbeda, dan karena itu saya tidak akan masuk ke dalam terminologi; lebih baik mari kita lihat beberapa contoh spesifik.

Struktur jaringan yang saya jelaskan hanya mampu mengenali atribut lokal dari satu spesies saja. Untuk mengenali gambar, kita membutuhkan lebih banyak peta fitur. Oleh karena itu, lapisan konvolusional selesai terdiri dari beberapa peta fitur yang berbeda:



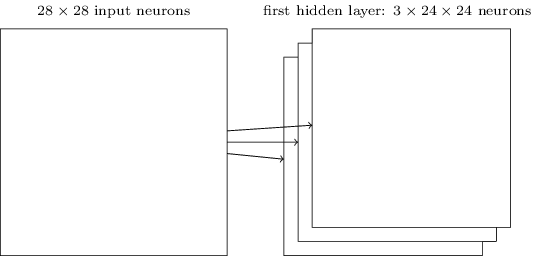
Contoh ini menunjukkan 3 peta fitur. Setiap kartu ditentukan oleh set bobot total 5x5 dan satu offset umum. Akibatnya, jaringan semacam itu dapat mengenali tiga jenis tanda yang berbeda, dan setiap tanda dapat ditemukan di bagian gambar mana pun.

Saya telah menggambar tiga kartu atribut untuk kesederhanaan. Dalam praktiknya, SNA dapat menggunakan lebih banyak (mungkin lebih banyak) peta fitur. Salah satu SNS awal, LeNet-5, menggunakan 6 kartu fitur, yang masing-masing dikaitkan dengan bidang reseptif 5x5, untuk mengenali angka MNIST. Oleh karena itu, contoh di atas sangat mirip dengan LeNet-5. Dalam contoh-contoh yang akan kami kembangkan secara mandiri lebih lanjut, kami akan menggunakan lapisan konvolusional yang berisi 20 dan 40 kartu fitur. Mari kita lihat tanda-tanda yang akan kita periksa:



20 gambar ini sesuai dengan 20 peta atribut yang berbeda (filter, atau kernel). Setiap kartu diwakili oleh gambar 5x5 sesuai dengan bobot 5x5 bidang reseptif lokal. Piksel putih berarti bobot rendah (biasanya lebih negatif), dan peta fitur bereaksi lebih sedikit terhadap pikselnya. Piksel yang lebih gelap berarti lebih berat, dan peta fitur lebih banyak bereaksi terhadap pikselnya. Secara kasar, gambar-gambar ini menunjukkan tanda-tanda yang ditanggapi oleh lapisan konvolusional.

Kesimpulan apa yang bisa diambil dari peta atribut ini? Struktur spasial di sini, jelas, tidak muncul secara acak - banyak tanda menunjukkan area yang terang dan gelap. Ini menunjukkan bahwa jaringan kami benar-benar mempelajari sesuatu yang berkaitan dengan struktur spasial. Namun, selain itu, agak sulit untuk memahami apa tanda-tanda ini. Kami jelas tidak mempelajari, katakanlah, filter Gabor , yang digunakan dalam banyak pendekatan tradisional untuk pengenalan pola. Bahkan, banyak pekerjaan sedang dilakukan sekarang untuk lebih memahami dengan tepat tanda-tanda mana yang dipelajari oleh SNA. Jika Anda tertarik, saya sarankan mulai dengan 2013 .

Keuntungan besar dari bobot dan offset umum adalah ini secara drastis mengurangi jumlah parameter yang tersedia untuk SNA. Untuk setiap peta fitur, kita membutuhkan 5 × 5 = 25 bobot total dan satu offset umum. Oleh karena itu, diperlukan 26 parameter untuk setiap peta fitur. Jika kita memiliki 20 peta fitur, maka secara total kita akan memiliki 20 × 26 = 520 parameter yang menentukan lapisan konvolusi. Sebagai perbandingan, anggaplah kita memiliki lapisan pertama yang terhubung penuh dengan 28 × 28 = 784 neuron yang masuk dan 30 neuron tersembunyi yang relatif sederhana - kami menggunakan skema ini dalam banyak contoh sebelumnya. Ternyata bobot 784 × 30, ditambah 30 offset, total 23.550 parameter. Dengan kata lain, lapisan yang terhubung sepenuhnya akan memiliki parameter lebih dari 40 kali lebih banyak daripada lapisan konvolusional.

Tentu saja, kita tidak dapat secara langsung membandingkan jumlah parameter, karena kedua model ini berbeda secara radikal. Tetapi secara intuitif tampaknya menggunakan invarian translasi konvolusional mengurangi jumlah parameter yang diperlukan untuk mencapai efisiensi yang sebanding dengan model yang sepenuhnya terhubung. Dan ini, pada gilirannya, akan mempercepat pelatihan model convolutional, dan pada akhirnya membantu kita menciptakan jaringan yang lebih dalam menggunakan lapisan convolutional.

Omong-omong, nama "konvolusional" berasal dari operasi dalam persamaan (125), yang kadang-kadang disebut konvolusi . Lebih tepatnya, kadang-kadang orang menulis persamaan ini sebagai ¹ = σ (b + w ∗ a ⁰ ), di mana ¹ menunjukkan seperangkat aktivasi output dari satu kartu fitur, ⁰ - satu set aktivasi input, dan * disebut operasi konvolusi. Kami tidak akan menggali jauh ke dalam matematika konvolusi, jadi Anda tidak perlu khawatir terutama tentang koneksi ini. Tapi itu hanya layak diketahui dari mana nama itu berasal.

Lapisan pooling

Selain lapisan convolutional yang dijelaskan dalam SNA, ada juga lapisan penyatuan. Mereka biasanya digunakan segera setelah convolutional. Mereka berkomitmen untuk menyederhanakan informasi dari keluaran lapisan konvolusional.

Di sini saya menggunakan frase "peta fitur" tidak dalam arti fungsi yang dihitung oleh lapisan convolutional, tetapi untuk menunjukkan aktivasi output dari neuron lapisan tersembunyi. Penggunaan istilah semacam itu sering ditemukan dalam literatur penelitian.

Lapisan penyatuan menerima output dari setiap peta fitur lapisan konvolusi dan menyiapkan peta fitur terkompresi. Sebagai contoh, setiap elemen dari lapisan kumpulan dapat meringkas bagian, katakanlah, 2x2 neuron dari lapisan sebelumnya. Studi kasus: Satu prosedur pengumpulan yang umum dikenal sebagai max pooling. Dalam max pooling, elemen pooling hanya memberikan aktivasi maksimum dari bagian 2x2, seperti yang ditunjukkan pada diagram:



Karena output dari neuron lapisan konvolusional memberikan nilai 24x24, setelah menarik kita mendapatkan 12x12 neuron.

Seperti disebutkan di atas, lapisan konvolusional biasanya menyiratkan sesuatu yang lebih dari satu peta fitur tunggal. Kami menerapkan pengumpulan maksimum untuk setiap peta fitur secara individual. Jadi, jika kita memiliki tiga peta fitur, konvolusi gabungan dan lapisan pengumpulan max akan terlihat seperti ini:



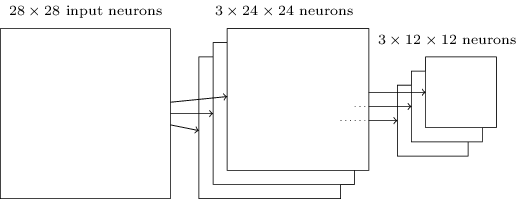Max-pulling dapat dibayangkan sebagai cara jaringan untuk bertanya apakah ada tanda yang diberikan di tempat gambar mana pun. Dan kemudian dia membuang informasi tentang lokasi tepatnya. Secara intuitif jelas bahwa ketika tanda ditemukan, lokasi tepatnya tidak lagi sama pentingnya dengan perkiraan lokasi relatif terhadap tanda-tanda lainnya. Keuntungannya adalah bahwa jumlah fitur yang diperoleh menggunakan penyatuan jauh lebih kecil, dan ini membantu mengurangi jumlah parameter yang diperlukan pada lapisan berikutnya.

Max pooling bukan satu-satunya teknologi pooling. Pendekatan umum lainnya dikenal sebagai pooling L2. Di dalamnya, alih-alih mengambil aktivasi maksimum dari wilayah 2x2 neuron, kita mengambil akar kuadrat dari jumlah kuadrat dari aktivasi wilayah 2x2. Rincian pendekatan berbeda, tetapi secara intuitif mirip dengan max-pooling: L2-pooling adalah cara untuk memampatkan informasi dari lapisan convolutional. Dalam praktiknya, kedua teknologi tersebut sering digunakan. Terkadang orang menggunakan jenis pooling lain. Jika Anda berjuang untuk mengoptimalkan kualitas jaringan, Anda dapat menggunakan data pendukung untuk membandingkan beberapa pendekatan berbeda untuk menarik, dan memilih yang terbaik. Tetapi kami tidak akan khawatir tentang optimasi yang begitu rinci.

Kesimpulannya

Sekarang kita bisa menyatukan semua informasi dan mendapatkan SNA yang lengkap. Ini mirip dengan arsitektur yang baru-baru ini kami tinjau, namun, ia memiliki lapisan tambahan 10 neuron keluaran yang sesuai dengan 10 nilai yang mungkin dari digit MNIST ('0', '1', '2', ..):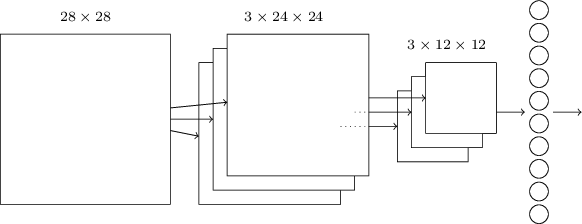



Jaringan dimulai dengan 28x28 neuron input yang digunakan untuk menyandikan intensitas piksel dari gambar MNIST. Setelah itu muncul lapisan convolutional menggunakan bidang reseptif lokal 5x5 dan 3 peta fitur. Hasilnya adalah lapisan 3x24x24 neuron sifat tersembunyi. Langkah selanjutnya adalah lapisan penggabungan maksimal yang diterapkan ke area 2x2 pada masing-masing dari tiga peta fitur. Hasilnya adalah lapisan 3x12x12 neuron ciri tersembunyi.

Lapisan koneksi terakhir dalam jaringan sepenuhnya terhubung. Yaitu, ia menghubungkan setiap neuron dari lapisan pengumpulan maks ke masing-masing dari 10 neuron keluaran. Kami menggunakan arsitektur yang sepenuhnya terhubung sebelumnya. Harap perhatikan bahwa dalam diagram di atas saya menggunakan panah tunggal untuk kesederhanaan, tidak menunjukkan semua tautan. Anda dapat dengan mudah membayangkan semuanya.

Arsitektur konvolusional ini sangat berbeda dari apa yang kami gunakan sebelumnya. Namun, gambaran keseluruhannya serupa: jaringan yang terdiri dari banyak elemen sederhana, yang perilakunya ditentukan oleh bobot dan offset. Tujuannya tetap sama: gunakan data pelatihan untuk melatih jaringan dalam bobot dan offset sehingga jaringan mengklasifikasikan angka yang masuk dengan baik.

Khususnya, seperti pada bab-bab sebelumnya, kami akan melatih jaringan kami menggunakan penurunan gradien stokastik dan propagasi balik. Prosedurnya hampir sama seperti sebelumnya. Namun, kita perlu membuat beberapa perubahan pada prosedur backpropagation. Faktanya adalah turunan kami untuk propagasi balik dimaksudkan untuk jaringan dengan lapisan yang sepenuhnya terhubung. Untungnya, mengubah turunan untuk lapisan convolutional dan max-pooling cukup sederhana. Jika Anda ingin memahami detailnya, saya mengundang Anda untuk mencoba menyelesaikan masalah berikut. Saya akan memperingatkan Anda bahwa itu akan memakan banyak waktu, kecuali jika Anda benar-benar memahami pertanyaan awal tentang diferensiasi backpropagation.

Tantangan

• . (BP1)-(BP4). , , - , . ?

Kami mendiskusikan ide di balik SNA. Mari kita lihat bagaimana mereka bekerja dalam praktik dengan mengimplementasikan beberapa SNA dan menerapkannya pada masalah klasifikasi digit MNIST. Kami akan menggunakan program network3.py, versi yang lebih baik dari program network.py dan network2.py yang dibuat di bab-bab sebelumnya. Program network3.py menggunakan ide-ide dari dokumentasi perpustakaan Theano (khususnya, implementasi LeNet-5 ), dari implementasi pengecualian dari Misha Denil dan Chris Olah . Kode program tersedia di GitHub. Di bagian selanjutnya, kita akan mempelajari kode program network3.py, dan di bagian ini kita akan menggunakannya sebagai pustaka untuk membuat SNA.

Program network.py dan network2.py ditulis dalam python menggunakan perpustakaan matriks Numpy. Mereka bekerja berdasarkan prinsip-prinsip pertama, dan mencapai perincian paling detail dari propagasi balik, penurunan gradien stokastik, dll. Tapi sekarang, ketika kita memahami detail ini, untuk network3.py kita akan menggunakan perpustakaan pembelajaran mesin Theano (lihat karya ilmiah dengan deskripsinya). Theano juga merupakan dasar dari perpustakaan populer untuk NS Pylearn2 dan Keras , serta Caffe dan Torch .

Menggunakan Theano memfasilitasi penerapan backpropagation di SNA, karena secara otomatis menghitung semua kartu. Theano juga terasa lebih cepat daripada kode kami sebelumnya (yang ditulis untuk memudahkan pemahaman, dan bukan untuk pekerjaan berkecepatan tinggi), jadi masuk akal untuk menggunakannya untuk melatih jaringan yang lebih kompleks. Secara khusus, salah satu fitur hebat Theano adalah menjalankan kode pada CPU dan GPU, jika tersedia. Berjalan pada GPU memberikan peningkatan kecepatan yang signifikan, dan membantu melatih jaringan yang lebih kompleks.

Untuk bekerja secara paralel dengan buku, Anda perlu menginstal Theano di sistem Anda. Untuk melakukan ini, ikuti instruksi pada halaman beranda proyek. Pada saat penulisan dan peluncuran contoh, Theano 0.7 tersedia. Saya menjalankan beberapa percobaan di Mac OS X Yosemite tanpa GPU. Beberapa di Ubuntu 14,04 dengan GPU NVIDIA. Dan beberapa ada di sana, dan di sana. Untuk memulai network3.py, atur bendera GPU dalam kode ke True atau False. Selain itu, instruksi berikut dapat membantu Anda menjalankan Theano di GPU Anda . Juga mudah untuk menemukan materi pelatihan online. Jika Anda tidak memiliki GPU sendiri, Anda dapat melihat ke Amazon Web Services EC2 G2. Tetapi bahkan dengan GPU, kode kami tidak akan bekerja dengan sangat cepat. Banyak percobaan akan berlangsung dari beberapa menit hingga beberapa jam. Yang paling kompleks dari mereka pada satu CPU akan dieksekusi selama beberapa hari. Seperti pada bab-bab sebelumnya, saya sarankan memulai eksperimen, dan melanjutkan membaca, secara berkala memeriksa operasinya. Tanpa menggunakan GPU, saya sarankan Anda mengurangi jumlah era pelatihan untuk eksperimen paling kompleks.

Untuk mendapatkan hasil dasar sebagai perbandingan, mari kita mulai dengan arsitektur dangkal dengan satu lapisan tersembunyi yang berisi 100 neuron tersembunyi. Kami akan mempelajari 60 era, menggunakan kecepatan belajar η = 0,1, ukuran paket mini adalah 10, dan kami akan belajar tanpa regularisasi.

Di bagian ini, saya menetapkan sejumlah era pelatihan tertentu. Saya melakukan ini untuk kejelasan dalam proses pembelajaran. Dalam praktiknya, berguna untuk menggunakan pemberhentian awal, melacak akurasi set konfirmasi, dan menghentikan pelatihan ketika kami yakin bahwa akurasi konfirmasi tidak lagi membaik:

>>> import network3 >>> from network3 import Network >>> from network3 import ConvPoolLayer, FullyConnectedLayer, SoftmaxLayer >>> training_data, validation_data, test_data = network3.load_data_shared() >>> mini_batch_size = 10 >>> net = Network([ FullyConnectedLayer(n_in=784, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data) 

Akurasi klasifikasi terbaik adalah 97,80%. Ini adalah akurasi klasifikasi test_data, diperkirakan dari era pelatihan, di mana kami mendapatkan akurasi klasifikasi terbaik untuk data dari validation_data. Menggunakan data yang divalidasi untuk membuat keputusan tentang penilaian akurasi membantu menghindari pelatihan ulang. Maka kita akan melakukannya. Hasil Anda mungkin sedikit berbeda, karena bobot dan offset jaringan diinisialisasi secara acak.

Akurasi 97,80% cukup dekat dengan akurasi 98,04% yang diperoleh pada Bab 3, menggunakan arsitektur jaringan yang sama dan pelatihan hiperparameter. Secara khusus, kedua contoh menggunakan jaringan dangkal dengan satu lapisan tersembunyi yang mengandung 100 neuron tersembunyi. Kedua jaringan mempelajari 60 era dengan ukuran paket mini 10 dan tingkat pembelajaran η = 0,1.

Namun, ada dua perbedaan dalam jaringan sebelumnya. Pertama, kami melakukan regularisasi untuk membantu mengurangi dampak pelatihan ulang. Mengatur jaringan saat ini meningkatkan akurasi, tetapi tidak banyak, jadi kami tidak akan memikirkannya untuk saat ini. Kedua, meskipun lapisan terakhir dari jaringan awal menggunakan aktivasi sigmoid dan fungsi biaya lintas-entropi, jaringan saat ini menggunakan lapisan terakhir dengan softmax, dan fungsi kemungkinan logaritmik sebagai fungsi biaya. Seperti dijelaskan dalam bab 3, ini bukan perubahan besar. Saya tidak beralih dari satu ke yang lain untuk beberapa alasan yang mendalam - terutama karena softmax dan fungsi kemungkinan logaritmik lebih sering digunakan dalam jaringan modern untuk mengklasifikasikan gambar.

Bisakah kita meningkatkan hasil menggunakan arsitektur jaringan yang lebih dalam?

Mari kita mulai dengan menyisipkan lapisan convolutional, di awal jaringan. Kami akan menggunakan bidang penerimaan lokal 5x5, panjang langkah 1 dan 20 kartu fitur. Kami juga akan memasukkan fitur penggabungan lapisan gabungan max menggunakan jendela penyatuan 2x2. Jadi arsitektur jaringan secara keseluruhan akan terlihat mirip dengan yang kita bahas di bagian sebelumnya, tetapi dengan lapisan tambahan yang terhubung sepenuhnya:



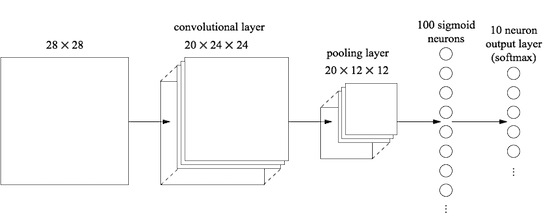
Dalam arsitektur ini, lapisan konvolusi dan penyatuan dilatih dalam struktur spasial lokal yang terkandung dalam gambar pelatihan yang masuk, dan lapisan terakhir yang terhubung sepenuhnya dilatih pada tingkat yang lebih abstrak, mengintegrasikan informasi global dari seluruh gambar. Ini adalah skema yang biasa digunakan dalam SNA.

Mari kita latih jaringan semacam itu, dan lihat bagaimana perilakunya.

 >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=20*12*12, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data) 

Kami mendapatkan akurasi 98,78%, yang jauh lebih tinggi daripada hasil sebelumnya. Kami mengurangi kesalahan lebih dari sepertiga - hasil yang sangat baik.

Menggambarkan struktur jaringan, saya menganggap lapisan convolutional dan pooling sebagai satu lapisan. Anggap mereka sebagai lapisan terpisah, atau sebagai lapisan tunggal - masalah preferensi. network3.py menganggap mereka sebagai satu lapisan, karena cara ini kode lebih kompak. Namun, mudah untuk memodifikasi network3.py sehingga lapisan dapat diatur secara individual.

Latihan

• Keakuratan klasifikasi apa yang akan kita dapatkan jika kita menurunkan lapisan yang sepenuhnya terhubung dan hanya menggunakan lapisan konvolusi / kolam dan lapisan softmax? Apakah dimasukkannya lapisan yang terhubung sepenuhnya membantu?

Bisakah kita meningkatkan hasilnya sebesar 98,78%?

Mari kita coba memasukkan lapisan konvolusi / penggabungan kedua. Kami akan menyisipkannya di antara konvolusi / penyatuan yang ada dan lapisan tersembunyi yang terhubung sepenuhnya. Kami lagi menggunakan bidang reseptif 5x5 lokal dan kolam di bagian 2x2. Mari kita lihat apa yang terjadi ketika kita melatih jaringan dengan hyperparameter yang kira-kira sama seperti sebelumnya:

 >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=40*4*4, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data) 

Dan lagi, kami memiliki peningkatan: sekarang kami mendapatkan akurasi 99,06%!

Saat ini, dua pertanyaan alami muncul. Pertama: apa artinya menggunakan lapisan konvolusi / penyatuan kedua? Anda dapat mengasumsikan bahwa pada lapisan konvolusi / penyatuan kedua, gambar "12x12" masuk ke input, yang "piksel" -nya mewakili keberadaan (atau tidak adanya) fitur-fitur lokal tertentu dalam gambar yang masuk asli. Artinya, kita dapat mengasumsikan bahwa versi tertentu dari gambar yang masuk asli datang ke input dari lapisan ini. Ini akan menjadi versi yang lebih abstrak dan ringkas, tetapi masih memiliki struktur spasial yang cukup, sehingga masuk akal untuk menggunakan konvolusi / lapisan tarikan kedua untuk memprosesnya.

Sudut pandang yang menyenangkan, tetapi menimbulkan pertanyaan kedua. Pada output dari lapisan sebelumnya, 20 KP terpisah diperoleh, oleh karena itu 20x12x12 kelompok data input masuk ke lapisan konvolusi / penggabungan kedua. Ternyata kita memiliki 20 gambar terpisah yang termasuk dalam lapisan konvolusi / kolam, dan bukan satu gambar, seperti halnya dengan lapisan konvolusi / kolam sebelumnya. Jadi bagaimana neuron dari lapisan konvolusi / lapisan kedua harus merespons banyak dari gambar yang masuk ini? Faktanya, kami mengizinkan setiap neuron dari lapisan ini dilatih berdasarkan semua neuron 20x5x5 yang memasuki bidang reseptif lokalnya. Dalam bahasa yang kurang formal, pendeteksi fitur pada lapisan konvolusi / lapisan kedua akan memiliki akses ke semua fitur pada lapisan pertama, tetapi hanya di dalam bidang penerimaan lokal spesifik mereka.

By the way, masalah seperti itu akan muncul di lapisan pertama, jika gambar berwarna. Dalam hal ini, kita akan memiliki 3 atribut input untuk setiap piksel yang sesuai dengan saluran merah, hijau dan biru dari gambar asli. Dan kemudian kami juga akan memberikan detektor tanda akses ke semua informasi warna, tetapi hanya dalam kerangka bidang penerimaan lokal mereka.

Tantangan

• Menggunakan fungsi aktivasi dalam bentuk tangen hiperbolik. Sebelumnya dalam buku ini, saya menyebutkan bukti beberapa kali bahwa fungsi tanh, sebuah garis singgung hiperbolik, mungkin lebih cocok untuk menjadi fungsi aktivasi daripada sigmoid. Kami tidak melakukan apa-apa dengan ini, karena kami memiliki kemajuan yang baik dengan sigmoid. Tapi mari kita coba beberapa eksperimen dengan tanh sebagai fungsi aktivasi. Cobalah untuk melatih jaringan tang-activated dengan lapisan convolutional dan sepenuhnya terhubung (Anda dapat melewati aktivasi_fn = tanh sebagai parameter ke kelas ConvPoolLayer dan FullyConnectedLayer). Mulailah dengan hyperparameter yang sama dengan yang dimiliki jaringan sigmoid, tetapi latih jaringan 20 era, bukan 60. Bagaimana perilaku jaringan? Apa yang akan terjadi jika kita melanjutkan hingga era ke-60? Cobalah untuk membangun grafik keakuratan konfirmasi kerja oleh zaman untuk tangen dan sigmoid, hingga era ke-60. Jika hasil Anda mirip dengan milik saya, Anda akan menemukan bahwa jaringan berbasis tangen belajar sedikit lebih cepat, tetapi akurasi yang dihasilkan dari kedua jaringan itu sama. Bisakah Anda jelaskan mengapa ini terjadi? Apakah mungkin untuk mencapai kecepatan belajar yang sama dengan sigmoid - misalnya, dengan mengubah kecepatan belajar atau melalui penskalaan (ingat bahwa σ (z) = (1 + tanh (z / 2)) / 2)? Coba lima atau enam hiperparameter atau arsitektur jaringan yang berbeda, cari di mana garis singgung berada di depan sigmoid. Saya perhatikan bahwa tugas ini terbuka. Secara pribadi, saya tidak menemukan keuntungan serius dalam beralih ke garis singgung, meskipun saya tidak melakukan eksperimen yang komprehensif, dan mungkin Anda akan menemukannya. Bagaimanapun, kami akan segera menemukan keuntungan dalam beralih ke fungsi aktivasi linier yang diluruskan, jadi kami tidak akan lagi mempelajari masalah tangen hiperbolik.

Menggunakan elemen linear yang diluruskan

Jaringan yang kami kembangkan saat ini adalah salah satu opsi jaringan yang digunakan dalam karya yang bermanfaat pada tahun 1998 , di mana tugas MNIST pertama kali diperkenalkan - jaringan yang disebut LeNet-5. Ini adalah dasar yang baik untuk percobaan lebih lanjut, untuk meningkatkan pemahaman tentang masalah dan intuisi. Secara khusus, ada banyak cara di mana kita dapat mengubah jaringan untuk mencari cara meningkatkan hasil.

Pertama, mari kita ubah neuron kita sehingga alih-alih menggunakan fungsi aktivasi sigmoid, kita dapat menggunakan elemen linear yang diluruskan (ReLU). Artinya, kita akan menggunakan fungsi aktivasi dari bentuk f (z) ≡ maks (0, z). Kami akan melatih jaringan 60 era, dengan kecepatan η = 0,03. Saya juga menemukan bahwa sedikit lebih nyaman untuk menggunakan regularisasi L2 dengan parameter regularisasi λ = 0,1:

 >>> from network3 import ReLU >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1) 

Saya mendapat akurasi klasifikasi 99,23%. Peningkatan sederhana dibandingkan hasil sigmoid (99,06%). Namun, dalam semua percobaan saya, saya menemukan bahwa jaringan berdasarkan ReLU berada di depan jaringan berdasarkan pada fungsi aktivasi sigmoid dengan keteguhan yang patut ditiru. Rupanya, ada keuntungan nyata dalam beralih ke ReLU untuk menyelesaikan masalah ini.

Apa yang membuat fungsi aktivasi ReLU lebih baik daripada singgung sigmoid atau hiperbolik? Saat ini, kami tidak terlalu memahami hal ini. Biasanya dikatakan bahwa fungsi maks (0, z) tidak jenuh pada z besar, tidak seperti neuron sigmoid, dan ini membantu neuron ReLU untuk terus belajar. Saya tidak berdebat, tetapi pembenaran ini tidak bisa disebut komprehensif, itu hanya semacam pengamatan (saya mengingatkan Anda bahwa kami membahas saturasi pada bab 2 ).

ReLU mulai digunakan secara aktif dalam beberapa tahun terakhir. Mereka diadopsi karena alasan empiris: beberapa orang mencoba ReLU, seringkali hanya berdasarkan firasat atau argumen heuristik. Mereka mendapat hasil yang baik, dan latihan itu menyebar. Di dunia yang ideal, kita akan memiliki teori yang memberi tahu kita aplikasi mana yang fungsi aktivasi terbaik untuk aplikasi mana. Tetapi untuk sekarang, kita masih memiliki jalan panjang untuk menghadapi situasi seperti itu. Saya tidak akan terkejut sama sekali jika perbaikan lebih lanjut dalam pengoperasian jaringan dapat diperoleh dengan memilih beberapa fungsi aktivasi yang lebih cocok. Saya juga berharap teori fungsi aktivasi yang baik akan dikembangkan dalam beberapa dekade mendatang. Tetapi hari ini kita harus mengandalkan aturan praktis dan pengalaman yang kurang dipelajari.

Perluasan data pelatihan

Cara lain yang mungkin dapat membantu kami meningkatkan hasil kami adalah dengan memperluas data pelatihan secara algoritmik. Cara termudah untuk memperluas data pelatihan adalah dengan menggeser setiap gambar pelatihan dengan satu piksel, atas, bawah, kanan atau kiri. Ini dapat dilakukan dengan menjalankan program expand_mnist.py .

 $ python expand_mnist.py 

Peluncuran program ini mengubah 50.000 gambar pelatihan MNIST menjadi 250.000 gambar pelatihan yang diperluas. Lalu kita bisa menggunakan gambar pelatihan ini untuk melatih jaringan. Kami akan menggunakan jaringan yang sama seperti sebelumnya dengan ReLU. Dalam percobaan pertama saya, saya mengurangi jumlah era pelatihan - ini masuk akal, karena kami memiliki data pelatihan 5 kali lebih banyak. Namun, memperluas kumpulan data secara signifikan mengurangi efek pelatihan ulang. Karena itu, setelah melakukan beberapa percobaan, saya kembali ke jumlah era 60. Bagaimanapun, mari kita latih:

 >>> expanded_training_data, _, _ = network3.load_data_shared( "../data/mnist_expanded.pkl.gz") >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1) 

Menggunakan data pelatihan tingkat lanjut, saya mendapatkan akurasi 99,37%. Perubahan yang hampir sepele seperti itu memberikan peningkatan signifikan dalam akurasi klasifikasi. Dan, seperti yang telah kita bahas sebelumnya, ekstensi data algoritmik dapat dikembangkan lebih lanjut. Sekadar mengingatkan Anda: pada tahun 2003, Simard, Steinkraus dan Platt meningkatkan akurasi jaringan mereka hingga 99,6%. Jaringan mereka mirip dengan kita, mereka menggunakan dua lapisan konvolusi / kolam, diikuti oleh lapisan yang sepenuhnya terhubung dengan 100 neuron. Detail arsitektur mereka bervariasi - mereka tidak memiliki kesempatan untuk mengambil keuntungan dari ReLU, misalnya - namun, kunci untuk meningkatkan kualitas pekerjaan adalah perluasan data pelatihan. Mereka mencapai ini dengan memutar, mentransfer, dan mendistorsi gambar pelatihan MNIST. Mereka juga mengembangkan proses "distorsi elastis", meniru getaran acak dari otot-otot lengan saat menulis. Dengan menggabungkan semua proses ini, mereka secara signifikan meningkatkan volume efektif dari basis data pelatihan mereka, dan karena itu, mencapai akurasi 99,6%.

Tantangan

• Gagasan lapisan konvolusional adalah untuk bekerja terlepas dari lokasi di gambar. Tapi mungkin aneh kalau jaringan kita lebih terlatih ketika kita hanya memindahkan gambar input. Bisakah Anda menjelaskan mengapa ini sebenarnya cukup masuk akal?

Menambahkan Lapisan Tambahan yang Terhubung Penuh

Apakah mungkin memperbaiki situasi? Satu kemungkinan adalah menggunakan prosedur yang sama persis, tetapi pada saat yang sama meningkatkan ukuran lapisan yang terhubung sepenuhnya. Saya menjalankan program dengan 300 dan dengan 1000 neuron, dan mendapat hasil masing-masing 99,46% dan 99,43%. Ini menarik, tetapi tidak terlalu meyakinkan dari hasil sebelumnya (99,37%).

Bagaimana dengan menambahkan lapisan ekstra yang sepenuhnya terhubung? Mari kita coba menambahkan lapisan yang terhubung sepenuhnya tambahan sehingga kita memiliki dua lapisan 100 neuron yang sepenuhnya terhubung:

 >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), FullyConnectedLayer(n_in=100, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1) 

Dengan demikian, saya mencapai akurasi verifikasi 99,43%. Jaringan yang diperluas lagi tidak banyak meningkatkan kinerja. Setelah melakukan percobaan serupa dengan lapisan yang terhubung penuh dari 300 dan 100 neuron, saya mendapatkan akurasi 99,48% dan 99,47%. Inspiratif, tetapi tidak seperti kemenangan nyata.

Apa yang sedang terjadi Apakah mungkin lapisan tambahan yang terhubung sepenuhnya atau tambahan tidak membantu menyelesaikan masalah MNIST? Atau bisakah jaringan kami mencapai lebih baik, tetapi kami mengembangkannya ke arah yang salah? Mungkin kita bisa, misalnya, menggunakan regularisasi yang lebih ketat untuk mengurangi pelatihan ulang. Salah satu kemungkinan adalah teknik putus sekolah yang disebutkan dalam bab 3. Ingat bahwa ide dasar pengecualian adalah untuk secara acak menghapus aktivasi individu saat melatih jaringan. Akibatnya, model menjadi lebih tahan terhadap hilangnya bukti individual, dan oleh karena itu kecil kemungkinannya akan bergantung pada beberapa fitur kecil non-standar dari data pelatihan. Mari kita coba menerapkan pengecualian pada lapisan yang terhubung sepenuhnya terakhir:

 >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer( n_in=40*4*4, n_out=1000, activation_fn=ReLU, p_dropout=0.5), FullyConnectedLayer( n_in=1000, n_out=1000, activation_fn=ReLU, p_dropout=0.5), SoftmaxLayer(n_in=1000, n_out=10, p_dropout=0.5)], mini_batch_size) >>> net.SGD(expanded_training_data, 40, mini_batch_size, 0.03, validation_data, test_data) 

Dengan menggunakan pendekatan ini, kami mencapai akurasi 99,60%, yang jauh lebih baik daripada yang sebelumnya, terutama penilaian dasar kami - jaringan dengan 100 neuron tersembunyi, yang memberikan akurasi 99,37%.

Dua perubahan patut dicatat di sini.

Pertama, saya mengurangi jumlah era pelatihan menjadi 40: pengecualian mengurangi pelatihan ulang, dan kami belajar lebih cepat.

Kedua, lapisan tersembunyi yang terhubung penuh mengandung 1000 neuron, dan bukan 100, seperti sebelumnya. Tentu saja, pengecualian, pada kenyataannya, menghilangkan banyak neuron selama pelatihan, jadi kita harus mengharapkan semacam ekspansi. Bahkan, saya melakukan percobaan dengan 300 dan 1000 neuron, dan menerima konfirmasi yang sedikit lebih baik dalam kasus 1000 neuron.

Menggunakan Ensemble Jaringan

Cara mudah untuk meningkatkan efisiensi adalah dengan membuat beberapa jaringan saraf, dan kemudian meminta mereka untuk memilih klasifikasi yang lebih baik. Misalkan, misalnya, kami melatih 5 NS yang berbeda menggunakan resep di atas, dan masing-masing mencapai akurasi hampir 99,6%. Meskipun semua jaringan akan menunjukkan akurasi yang sama, mereka mungkin memiliki kesalahan yang berbeda karena inisialisasi acak yang berbeda. Masuk akal untuk mengasumsikan bahwa jika 5 NA memilih, klasifikasi umum mereka akan lebih baik daripada jaringan mana pun secara terpisah.

Kedengarannya terlalu bagus untuk menjadi kenyataan, tetapi merakit ansambel seperti itu adalah trik umum untuk Majelis Nasional dan teknik-teknik MO lainnya. Dan itu benar-benar memberikan peningkatan efisiensi: kami mendapatkan akurasi 99,67%. Dengan kata lain, rangkaian jaringan kami dengan benar mengklasifikasikan 10.000 gambar verifikasi, dengan pengecualian 33.

Kesalahan yang tersisa ditunjukkan di bawah ini. Label di sudut kanan atas adalah klasifikasi yang benar menurut data MNIST, dan di sudut kanan bawah adalah label yang diterima oleh ansambel jaringan:



Penting untuk memikirkan gambar-gambar itu. Dua digit pertama, 6 dan 5 adalah kesalahan nyata dari ansambel kami. Namun, mereka bisa dipahami, kesalahan seperti itu bisa dilakukan oleh manusia. 6 ini benar-benar sangat mirip dengan 0, dan 5 sangat mirip dengan 3. Gambar ketiga, seharusnya 8, benar-benar lebih mirip 9. Saya memihak ansambel jaringan: Saya pikir dia melakukan pekerjaan lebih baik daripada orang yang menulis angka ini. Di sisi lain, gambar keempat, 6, benar-benar salah diklasifikasikan oleh jaringan.

Dan sebagainya. Dalam kebanyakan kasus, solusi jaringan tampaknya masuk akal, dan dalam beberapa kasus mereka lebih baik mengklasifikasikan angka daripada orang yang menulisnya. Secara keseluruhan, jaringan kami menunjukkan efisiensi luar biasa, terutama jika kami ingat bahwa mereka mengklasifikasikan 9967 gambar dengan benar, yang tidak kami sajikan di sini.Dalam konteks ini, beberapa kesalahan jelas dapat dipahami. Bahkan orang yang berhati-hati pun terkadang keliru. Karena itu, saya dapat mengharapkan hasil yang lebih baik hanya dari orang yang sangat akurat dan metodis. Jaringan kami mendekati kinerja manusia.

Mengapa kami menerapkan pengecualian hanya pada lapisan yang sepenuhnya terhubung

Jika Anda memperhatikan kode di atas, Anda akan melihat bahwa kami menerapkan pengecualian hanya untuk lapisan jaringan yang sepenuhnya terhubung, tetapi tidak untuk yang konvolusional. Pada prinsipnya, prosedur serupa dapat diterapkan pada lapisan konvolusional. Tetapi tidak perlu untuk ini: lapisan konvolusional memiliki resistensi bawaan yang signifikan terhadap pelatihan ulang. Ini karena bobot total membuat filter konvolusional belajar di seluruh gambar sekaligus. Akibatnya, mereka cenderung tersandung beberapa distorsi lokal dalam data pelatihan. Oleh karena itu, tidak ada kebutuhan khusus untuk menerapkan regulator lain kepada mereka, seperti pengecualian.

Pindah

Anda dapat meningkatkan efisiensi memecahkan masalah MNIST bahkan lebih. Rodrigo Benenson mengumpulkan tablet informatif yang menunjukkan kemajuan selama bertahun-tahun, dan tautan ke pekerjaan. Banyak karya menggunakan GSS dengan cara yang sama seperti kita menggunakannya. Jika Anda menggeledah pekerjaan Anda, Anda akan menemukan banyak teknik menarik, dan Anda mungkin ingin menerapkan beberapa dari mereka. Dalam hal ini, akan lebih bijaksana untuk memulai implementasi mereka dengan jaringan sederhana yang dapat dilatih dengan cepat, dan ini akan membantu Anda dengan cepat mulai memahami apa yang terjadi.

Sebagian besar, saya tidak akan mencoba meninjau pekerjaan terbaru. Tapi saya tidak bisa menolak satu pengecualian. Ini tentang satu pekerjaan pada tahun 2010. Saya suka kesederhanaannya. Jaringan ini multilayer, dan hanya menggunakan lapisan yang sepenuhnya terhubung (tanpa konvolusi). Di jaringan mereka yang paling sukses, ada lapisan tersembunyi yang masing-masing berisi 2500, 2000, 1500, 1000 dan 500 neuron. Mereka menggunakan ide serupa untuk memperluas data pelatihan. Namun di samping itu, mereka menerapkan beberapa trik lagi, termasuk kurangnya lapisan konvolusional: itu adalah jaringan vanilla yang paling sederhana, yang, dengan kesabaran yang tepat dan ketersediaan kemampuan komputer yang sesuai, dapat diajarkan pada tahun 1980-an (jika set MNIST ada saat itu). Mereka mencapai akurasi klasifikasi 99,65%, yang kira-kira sama dengan kita. Hal utama dalam pekerjaan mereka adalah penggunaan jaringan yang sangat besar dan dalam, dan penggunaan GPU untuk mempercepat pembelajaran. Ini memungkinkan mereka untuk belajar banyak era. Mereka juga mengambil keuntungan dari lamanya interval pelatihan,dan secara bertahap mengurangi kecepatan belajar dari 10^-3 hingga 10 ^-6 . Mencoba mencapai hasil yang serupa dengan arsitektur seperti milik mereka adalah latihan yang menarik.

Mengapa kita bisa belajar?

Pada bab sebelumnya, kami melihat hambatan mendasar untuk mempelajari NS multilayer yang mendalam. Secara khusus, kami melihat bahwa gradien menjadi sangat tidak stabil: ketika bergerak dari lapisan output ke yang sebelumnya, gradien cenderung menghilang (masalah gradien menghilang) atau pertumbuhan eksplosif (masalah pertumbuhan gradien eksplosif). Karena gradien adalah sinyal yang kami gunakan untuk pelatihan, ini menyebabkan masalah.

Bagaimana kami berhasil menghindarinya?

Jawabannya, secara alami, adalah ini: kami tidak dapat menghindarinya. Sebaliknya, kami melakukan beberapa hal yang memungkinkan kami untuk terus bekerja, meskipun demikian. Secara khusus: (1) penggunaan lapisan konvolusional sangat mengurangi jumlah parameter yang terkandung di dalamnya, sangat memfasilitasi masalah pembelajaran; (2) penggunaan teknik regularisasi yang lebih efisien (pengecualian dan lapisan konvolusional); (3) menggunakan ReLU alih-alih neuron sigmoid untuk mempercepat pembelajaran - secara empiris hingga 3-5 kali; (4) penggunaan GPU dan kemampuan untuk belajar dari waktu ke waktu. Secara khusus, dalam percobaan terbaru, kami mempelajari 40 era menggunakan kumpulan data 5 kali lebih besar dari data pelatihan MNIST standar. Sebelumnya dalam buku ini, kami mempelajari 30 era dengan menggunakan data pelatihan standar. Kombinasi faktor (3) dan (4) memberikan efek seperti itu,seolah-olah kita belajar 30 kali lebih lama dari sebelumnya.

Anda mungkin berkata, "Apakah hanya itu?" Apakah hanya itu yang diperlukan untuk melatih jaringan saraf yang dalam? Dan karena apa keributan itu kemudian terbakar? ”

Tentu saja, kami menggunakan ide lain: set data yang cukup besar (untuk membantu menghindari pelatihan ulang); fungsi biaya yang benar (untuk menghindari perlambatan belajar); inisialisasi bobot yang baik (juga untuk menghindari pembelajaran yang lambat karena saturasi neuron); ekstensi algoritmik dari set data pelatihan. Kami membahas ini dan ide-ide lain di bab-bab sebelumnya, dan biasanya kami memiliki kesempatan untuk menggunakannya kembali dengan catatan kecil di bab ini.

Dari semua indikasi, ini adalah serangkaian ide yang cukup sederhana. Sederhana, bagaimanapun, mampu banyak ketika digunakan di kompleks. Ternyata memulai dengan pembelajaran yang dalam sangat mudah!

?

Jika kita menganggap lapisan konvolusi / penggabungan sebagai satu, maka dalam arsitektur akhir kita ada 4 lapisan tersembunyi. Apakah jaringan seperti itu layak mendapat gelar yang mendalam? Secara alami, 4 layer tersembunyi jauh lebih banyak daripada di jaringan dangkal yang telah kita pelajari sebelumnya. Sebagian besar jaringan memiliki satu lapisan tersembunyi, kadang-kadang 2. Di sisi lain, jaringan modern modern terkadang memiliki puluhan lapisan tersembunyi. Kadang-kadang saya bertemu orang-orang yang berpikir bahwa semakin dalam jaringan, semakin baik, dan bahwa jika Anda tidak menggunakan sejumlah besar lapisan tersembunyi, itu berarti Anda tidak benar-benar melakukan pembelajaran mendalam. Saya tidak berpikir begitu, khususnya karena pendekatan seperti itu mengubah definisi pembelajaran mendalam menjadi prosedur yang tergantung pada hasil sesaat. Sebuah terobosan nyata di bidang ini adalah gagasan tentang kepraktisan melampaui jaringan dengan satu atau dua lapisan tersembunyi,berlaku pada pertengahan 2000-an. Ini adalah terobosan nyata, membuka bidang penelitian dengan model yang lebih ekspresif. Nah, sejumlah lapisan tertentu bukan merupakan kepentingan mendasar. Penggunaan jaringan yang dalam adalah alat untuk mencapai tujuan lain, seperti meningkatkan akurasi klasifikasi.

Masalah prosedural

Pada bagian ini, kami dengan lancar beralih dari jaringan dangkal dengan satu lapisan tersembunyi ke jaringan konvolusi multi-lapisan. Segalanya tampak begitu mudah! Kami membuat perubahan dan mendapat peningkatan. Jika Anda mulai bereksperimen, saya jamin bahwa biasanya semuanya tidak akan berjalan dengan lancar. Saya menyajikan kepada Anda kisah yang disisir, menghilangkan banyak percobaan, termasuk yang tidak berhasil. Saya harap cerita yang disisir ini akan membantu Anda lebih memahami ide-ide dasar. Tapi dia berisiko menyampaikan kesan yang tidak lengkap. Untuk mendapatkan jaringan yang baik dan berfungsi membutuhkan banyak percobaan dan kesalahan, diselingi dengan frustrasi. Dalam praktiknya, Anda dapat mengharapkan sejumlah besar percobaan. Untuk mempercepat proses, informasi dalam Bab 3 tentang pemilihan hyperparameter jaringan, serta literatur tambahan yang disebutkan di sana, dapat membantu Anda.

Kode untuk jaringan konvolusi kami

Baiklah, sekarang mari kita lihat kode untuk program network3.py kami. Secara struktural, ini mirip dengan network2.py, yang kami kembangkan di bab 3, tetapi detailnya berbeda karena penggunaan perpustakaan Theano. Mari kita mulai dengan kelas FullyConnectedLayer, mirip dengan lapisan yang kita pelajari sebelumnya.

 class FullyConnectedLayer(object): def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0): self.n_in = n_in self.n_out = n_out self.activation_fn = activation_fn self.p_dropout = p_dropout # Initialize weights and biases self.w = theano.shared( np.asarray( np.random.normal( loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)), dtype=theano.config.floatX), name='w', borrow=True) self.b = theano.shared( np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)), dtype=theano.config.floatX), name='b', borrow=True) self.params = [self.w, self.b] def set_inpt(self, inpt, inpt_dropout, mini_batch_size): self.inpt = inpt.reshape((mini_batch_size, self.n_in)) self.output = self.activation_fn( (1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b) self.y_out = T.argmax(self.output, axis=1) self.inpt_dropout = dropout_layer( inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout) self.output_dropout = self.activation_fn( T.dot(self.inpt_dropout, self.w) + self.b) def accuracy(self, y): "Return the accuracy for the mini-batch." return T.mean(T.eq(y, self.y_out)) 

Sebagian besar metode __init__ berbicara sendiri, tetapi beberapa catatan dapat membantu memperjelas kode. Seperti biasa, kami menginisialisasi bobot dan offset menggunakan nilai acak normal dengan standar deviasi yang sesuai. Garis-garis ini terlihat sedikit tidak bisa dipahami. Namun, sebagian besar kode aneh memuat bobot dan penyeimbang ke dalam apa yang disebut perpustakaan Theano variabel bersama. Ini memastikan bahwa variabel dapat diproses pada GPU, jika tersedia. Kami tidak akan membahas masalah ini - jika tertarik, baca dokumentasi untuk Theano. Juga perhatikan bahwa inisialisasi bobot dan offset ini untuk fungsi aktivasi sigmoid. Idealnya, untuk fungsi seperti singgung hiperbolik dan ReLU, kami akan menginisialisasi bobot dan offset secara berbeda. Masalah ini dibahas dalam tugas di masa mendatang.Metode __init__ berakhir dengan pernyataan self.params = [self.w, self.b]. Ini adalah cara yang mudah untuk menyatukan semua parameter pembelajaran yang terkait dengan layer. Network.SGD kemudian menggunakan atribut params untuk mencari tahu variabel mana dalam instance kelas Network yang bisa dilatih.

Metode set_inpt digunakan untuk meneruskan input ke layer dan menghitung output yang sesuai. Saya menulis inpt daripada input, karena input adalah fungsi python bawaan, dan jika Anda bermain dengannya, ini dapat menyebabkan perilaku program yang tidak dapat diprediksi dan sulit untuk mendiagnosis kesalahan. Faktanya, kami memberikan masukan dalam dua cara: melalui self.inpt dan self.inpt_dropout. Ini dilakukan karena kami mungkin ingin menggunakan pengecualian selama pelatihan. Dan kemudian kita perlu menghapus sebagian dari neuron self.p_dropout. Inilah yang fungsi dropout_layer di baris kedua dari metode set_inpt. Jadi, self.inpt_dropout dan self.output_dropout digunakan selama pelatihan, dan self.inpt_dropout digunakan untuk semua tujuan lain, misalnya, mengevaluasi akurasi data validasi dan pengujian.

Definisi kelas untuk ConvPoolLayer dan SoftmaxLayer mirip dengan FullyConnectedLayer. Begitu mirip sehingga saya bahkan tidak akan mengutip kode. Jika Anda tertarik, kode lengkap program ini dapat dipelajari nanti di bab ini.

Perlu disebutkan beberapa detail berbeda. Jelas, di ConvPoolLayer dan SoftmaxLayer, kami menghitung aktivasi keluaran dengan cara yang sesuai dengan jenis lapisan. Untungnya, Theano mudah dilakukan, ia memiliki operasi bawaan untuk menghitung konvolusi, max-pooling, dan fungsi softmax.

Tidak terlalu jelas bagaimana menginisialisasi bobot dan offset di lapisan softmax - kami tidak membahas ini. Kami menyebutkan bahwa untuk lapisan berat sigmoidal, perlu menginisialisasi distribusi acak normal berparameter dengan tepat. Tetapi argumen heuristik ini diterapkan pada neuron sigmoid (dan, dengan koreksi kecil, pada tang neuron). Namun, tidak ada alasan khusus untuk argumen ini untuk diterapkan pada lapisan softmax. Oleh karena itu, tidak ada alasan untuk apriori menerapkan inisialisasi ini lagi. Sebagai gantinya, saya menginisialisasi semua bobot dan offset ke 0. Opsi ini spontan, tetapi dalam praktiknya cukup baik.

Jadi, kami telah mempelajari semua kelas lapisan. Bagaimana dengan kelas Jaringan? Mari kita mulai dengan menjelajahi metode __init__:

 class Network(object): def __init__(self, layers, mini_batch_size): """   layers,   ,   mini_batch_size          """ self.layers = layers self.mini_batch_size = mini_batch_size self.params = [param for layer in self.layers for param in layer.params] self.x = T.matrix("x") self.y = T.ivector("y") init_layer = self.layers[0] init_layer.set_inpt(self.x, self.x, self.mini_batch_size) for j in xrange(1, len(self.layers)): prev_layer, layer = self.layers[j-1], self.layers[j] layer.set_inpt( prev_layer.output, prev_layer.output_dropout, self.mini_batch_size) self.output = self.layers[-1].output self.output_dropout = self.layers[-1].output_dropout 

Sebagian besar kode berbicara sendiri. Baris self.params = [param untuk lapisan dalam ...] mengumpulkan semua parameter untuk setiap lapisan ke dalam satu daftar. Seperti yang disarankan sebelumnya, metode Network.SGD menggunakan self.params untuk mencari tahu parameter mana yang dapat dipelajari Jaringan. Baris self.x = T.matrix ("x") dan self.y = T.ivector ("y") mendefinisikan variabel simbol Theano x dan y. Mereka akan mewakili input dan output yang diinginkan dari jaringan.

Ini bukan tutorial tentang penggunaan Theano, jadi saya tidak akan membahas apa arti variabel simbolik (lihat dokumentasi , dan juga salah satu artikel tutorial) Secara kasar, mereka menunjukkan variabel matematika, bukan yang spesifik. Dengan mereka, Anda dapat melakukan banyak operasi biasa: menambah, mengurangi, melipatgandakan, menerapkan fungsi, dan sebagainya. Theano menyediakan banyak kemungkinan untuk memanipulasi variabel simbolik seperti itu, berbelit-belit, max-pulling, dan sebagainya. Namun, hal utama adalah kemungkinan diferensiasi simbolik cepat menggunakan bentuk yang sangat umum dari algoritma backpropagation. Ini sangat berguna untuk menerapkan keturunan gradien stokastik ke berbagai arsitektur jaringan. Secara khusus, baris kode berikut menentukan output simbolik dari jaringan. Kami mulai dengan menetapkan input ke lapisan pertama:

  init_layer.set_inpt(self.x, self.x, self.mini_batch_size) 

Input data ditransmisikan satu paket mini pada suatu waktu, sehingga ukurannya ditunjukkan di sana. Kami melewatkan input self.x dua kali: faktanya adalah kami dapat menggunakan jaringan dengan dua cara berbeda (dengan atau tanpa pengecualian). Untuk loop menyebarkan variabel simbolis self.x melalui lapisan Jaringan. Ini memungkinkan kita untuk mendefinisikan keluaran atribut akhir dan output_dropout, yang secara simbolis mewakili keluaran Jaringan.

Setelah berurusan dengan inisialisasi Jaringan, mari kita lihat pelatihannya melalui metode SGD. Kode terlihat panjang, tetapi strukturnya cukup sederhana. Penjelasan ikuti kode:

  def SGD(self, training_data, epochs, mini_batch_size, eta, validation_data, test_data, lmbda=0.0): """    -    .""" training_x, training_y = training_data validation_x, validation_y = validation_data test_x, test_y = test_data #   -  ,    num_training_batches = size(training_data)/mini_batch_size num_validation_batches = size(validation_data)/mini_batch_size num_test_batches = size(test_data)/mini_batch_size #    ,     l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers]) cost = self.layers[-1].cost(self)+\ 0.5*lmbda*l2_norm_squared/num_training_batches grads = T.grad(cost, self.params) updates = [(param, param-eta*grad) for param, grad in zip(self.params, grads)] #     -    #      -. i = T.lscalar() # mini-batch index train_mb = theano.function( [i], cost, updates=updates, givens={ self.x: training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size], self.y: training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size] }) validate_mb_accuracy = theano.function( [i], self.layers[-1].accuracy(self.y), givens={ self.x: validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size], self.y: validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size] }) test_mb_accuracy = theano.function( [i], self.layers[-1].accuracy(self.y), givens={ self.x: test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size], self.y: test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size] }) self.test_mb_predictions = theano.function( [i], self.layers[-1].y_out, givens={ self.x: test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size] }) #    best_validation_accuracy = 0.0 for epoch in xrange(epochs): for minibatch_index in xrange(num_training_batches): iteration = num_training_batches*epoch+minibatch_index if iteration print("Training mini-batch number {0}".format(iteration)) cost_ij = train_mb(minibatch_index) if (iteration+1) validation_accuracy = np.mean( [validate_mb_accuracy(j) for j in xrange(num_validation_batches)]) print("Epoch {0}: validation accuracy {1:.2 epoch, validation_accuracy)) if validation_accuracy >= best_validation_accuracy: print("This is the best validation accuracy to date.") best_validation_accuracy = validation_accuracy best_iteration = iteration if test_data: test_accuracy = np.mean( [test_mb_accuracy(j) for j in xrange(num_test_batches)]) print('The corresponding test accuracy is {0:.2 test_accuracy)) print("Finished training network.") print("Best validation accuracy of {0:.2 best_validation_accuracy, best_iteration)) print("Corresponding test accuracy of {0:.2 

Baris pertama jelas, mereka membagi set data menjadi komponen x dan y, dan menghitung jumlah paket mini yang digunakan dalam setiap set data. Baris berikut lebih menarik, dan mereka menunjukkan mengapa sangat menarik untuk bekerja dengan perpustakaan Theano. Saya akan mengutipnya di sini:

  #    ,     l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers]) cost = self.layers[-1].cost(self)+\ 0.5*lmbda*l2_norm_squared/num_training_batches grads = T.grad(cost, self.params) updates = [(param, param-eta*grad) for param, grad in zip(self.params, grads)] 

Dalam baris ini, kami secara simbolis mendefinisikan fungsi biaya yang diregulasi berdasarkan fungsi kemungkinan logaritmik, menghitung turunan yang sesuai dalam fungsi gradien, dan juga pembaruan parameter terkait. Theano memungkinkan kita melakukan semua ini hanya dalam beberapa baris. Satu-satunya hal yang disembunyikan adalah bahwa perhitungan biaya melibatkan pemanggilan metode biaya untuk lapisan output; kode ini terletak di tempat lain di network3.py. Tetapi ini singkat dan sederhana. Dengan definisi semua ini, semuanya siap untuk mendefinisikan fungsi train_mb, fungsi simbol Theano yang menggunakan pembaruan untuk memperbarui parameter jaringan dengan indeks paket mini. Demikian pula, fungsi validate_mb_accuracy dan test_mb_accuracy menghitung akurasi jaringan pada setiap paket mini yang diberikan data validasi atau verifikasi. Rata-rata dari fungsi-fungsi ini,kita dapat menghitung akurasi pada seluruh set data validasi dan verifikasi.

Sisa dari metode SGD berbicara untuk dirinya sendiri - kami hanya melalui zaman, melatih jaringan lagi dan lagi pada paket-paket kecil data pelatihan, dan kami menghitung akurasi konfirmasi dan verifikasi.

Sekarang kami memahami bagian terpenting dari tahun ini network3.py. Mari kita membahas seluruh program secara singkat. Anda tidak perlu mempelajari semuanya secara terperinci, tetapi Anda mungkin ingin membahasnya, dan mungkin mempelajari beberapa bagian yang sangat disukai. Tetapi, tentu saja, cara terbaik untuk memahami program adalah mengubahnya, menambahkan sesuatu yang baru, memperbaiki bagian-bagian yang, menurut Anda, dapat ditingkatkan. Setelah kode, saya menyajikan beberapa tugas yang berisi sejumlah saran awal tentang apa yang bisa dilakukan di sini. Ini kodenya.

 """network3.py ~~~~~~~~~~~~~~     Theano      .     (, , -, softmax)    (,  , ReLU;   ).    CPU     ,  network.py  network2.py. ,    ,      GPU,    .     Theano,       network.py  network2.py.  ,       .  , API   network2.py.       ,  ,     .   ,     ,    .      Theano   (http://deeplearning.net/tutorial/lenet.html ),       (https://github.com/mdenil/dropout )      (http://colah.imtqy.com ).   Theano 0.6  0.7,       . """ ####  #  import cPickle import gzip #  import numpy as np import theano import theano.tensor as T from theano.tensor.nnet import conv from theano.tensor.nnet import softmax from theano.tensor import shared_randomstreams from theano.tensor.signal import downsample #    def linear(z): return z def ReLU(z): return T.maximum(0.0, z) from theano.tensor.nnet import sigmoid from theano.tensor import tanh ####  GPU = True if GPU: print "Trying to run under a GPU. If this is not desired, then modify "+\ "network3.py\nto set the GPU flag to False." try: theano.config.device = 'gpu' except: pass # it's already set theano.config.floatX = 'float32' else: print "Running with a CPU. If this is not desired, then the modify "+\ "network3.py to set\nthe GPU flag to True." ####   MNIST def load_data_shared(filename="../data/mnist.pkl.gz"): f = gzip.open(filename, 'rb') training_data, validation_data, test_data = cPickle.load(f) f.close() def shared(data): """    .   Theano    GPU,   . """ shared_x = theano.shared( np.asarray(data[0], dtype=theano.config.floatX), borrow=True) shared_y = theano.shared( np.asarray(data[1], dtype=theano.config.floatX), borrow=True) return shared_x, T.cast(shared_y, "int32") return [shared(training_data), shared(validation_data), shared(test_data)] ####        class Network(object): def __init__(self, layers, mini_batch_size): """   layers,   ,   mini_batch_size         . """ self.layers = layers self.mini_batch_size = mini_batch_size self.params = [param for layer in self.layers for param in layer.params] self.x = T.matrix("x") self.y = T.ivector("y") init_layer = self.layers[0] init_layer.set_inpt(self.x, self.x, self.mini_batch_size) for j in xrange(1, len(self.layers)): prev_layer, layer = self.layers[j-1], self.layers[j] layer.set_inpt( prev_layer.output, prev_layer.output_dropout, self.mini_batch_size) self.output = self.layers[-1].output self.output_dropout = self.layers[-1].output_dropout def SGD(self, training_data, epochs, mini_batch_size, eta, validation_data, test_data, lmbda=0.0): """    -    .""" training_x, training_y = training_data validation_x, validation_y = validation_data test_x, test_y = test_data #   -  ,    num_training_batches = size(training_data)/mini_batch_size num_validation_batches = size(validation_data)/mini_batch_size num_test_batches = size(test_data)/mini_batch_size #    ,     l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers]) cost = self.layers[-1].cost(self)+\ 0.5*lmbda*l2_norm_squared/num_training_batches grads = T.grad(cost, self.params) updates = [(param, param-eta*grad) for param, grad in zip(self.params, grads)] #     -    #      -. i = T.lscalar() # mini-batch index train_mb = theano.function( [i], cost, updates=updates, givens={ self.x: training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size], self.y: training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size] }) validate_mb_accuracy = theano.function( [i], self.layers[-1].accuracy(self.y), givens={ self.x: validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size], self.y: validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size] }) test_mb_accuracy = theano.function( [i], self.layers[-1].accuracy(self.y), givens={ self.x: test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size], self.y: test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size] }) self.test_mb_predictions = theano.function( [i], self.layers[-1].y_out, givens={ self.x: test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size] }) #    best_validation_accuracy = 0.0 for epoch in xrange(epochs): for minibatch_index in xrange(num_training_batches): iteration = num_training_batches*epoch+minibatch_index if iteration % 1000 == 0: print("Training mini-batch number {0}".format(iteration)) cost_ij = train_mb(minibatch_index) if (iteration+1) % num_training_batches == 0: validation_accuracy = np.mean( [validate_mb_accuracy(j) for j in xrange(num_validation_batches)]) print("Epoch {0}: validation accuracy {1:.2%}".format( epoch, validation_accuracy)) if validation_accuracy >= best_validation_accuracy: print("This is the best validation accuracy to date.") best_validation_accuracy = validation_accuracy best_iteration = iteration if test_data: test_accuracy = np.mean( [test_mb_accuracy(j) for j in xrange(num_test_batches)]) print('The corresponding test accuracy is {0:.2%}'.format( test_accuracy)) print("Finished training network.") print("Best validation accuracy of {0:.2%} obtained at iteration {1}".format( best_validation_accuracy, best_iteration)) print("Corresponding test accuracy of {0:.2%}".format(test_accuracy)) ####    class ConvPoolLayer(object): """     - .        ,         ,    ,   . """ def __init__(self, filter_shape, image_shape, poolsize=(2, 2), activation_fn=sigmoid): """`filter_shape` -   4,   ,    ,     . `image_shape` -   4,   -,    ,    . `poolsize` -   2,    y  x. """ self.filter_shape = filter_shape self.image_shape = image_shape self.poolsize = poolsize self.activation_fn=activation_fn # initialize weights and biases n_out = (filter_shape[0]*np.prod(filter_shape[2:])/np.prod(poolsize)) self.w = theano.shared( np.asarray( np.random.normal(loc=0, scale=np.sqrt(1.0/n_out), size=filter_shape), dtype=theano.config.floatX), borrow=True) self.b = theano.shared( np.asarray( np.random.normal(loc=0, scale=1.0, size=(filter_shape[0],)), dtype=theano.config.floatX), borrow=True) self.params = [self.w, self.b] def set_inpt(self, inpt, inpt_dropout, mini_batch_size): self.inpt = inpt.reshape(self.image_shape) conv_out = conv.conv2d( input=self.inpt, filters=self.w, filter_shape=self.filter_shape, image_shape=self.image_shape) pooled_out = downsample.max_pool_2d( input=conv_out, ds=self.poolsize, ignore_border=True) self.output = self.activation_fn( pooled_out + self.b.dimshuffle('x', 0, 'x', 'x')) self.output_dropout = self.output # no dropout in the convolutional layers class FullyConnectedLayer(object): def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0): self.n_in = n_in self.n_out = n_out self.activation_fn = activation_fn self.p_dropout = p_dropout # Initialize weights and biases self.w = theano.shared( np.asarray( np.random.normal( loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)), dtype=theano.config.floatX), name='w', borrow=True) self.b = theano.shared( np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)), dtype=theano.config.floatX), name='b', borrow=True) self.params = [self.w, self.b] def set_inpt(self, inpt, inpt_dropout, mini_batch_size): self.inpt = inpt.reshape((mini_batch_size, self.n_in)) self.output = self.activation_fn( (1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b) self.y_out = T.argmax(self.output, axis=1) self.inpt_dropout = dropout_layer( inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout) self.output_dropout = self.activation_fn( T.dot(self.inpt_dropout, self.w) + self.b) def accuracy(self, y): "Return the accuracy for the mini-batch." return T.mean(T.eq(y, self.y_out)) class SoftmaxLayer(object): def __init__(self, n_in, n_out, p_dropout=0.0): self.n_in = n_in self.n_out = n_out self.p_dropout = p_dropout #     self.w = theano.shared( np.zeros((n_in, n_out), dtype=theano.config.floatX), name='w', borrow=True) self.b = theano.shared( np.zeros((n_out,), dtype=theano.config.floatX), name='b', borrow=True) self.params = [self.w, self.b] def set_inpt(self, inpt, inpt_dropout, mini_batch_size): self.inpt = inpt.reshape((mini_batch_size, self.n_in)) self.output = softmax((1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b) self.y_out = T.argmax(self.output, axis=1) self.inpt_dropout = dropout_layer( inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout) self.output_dropout = softmax(T.dot(self.inpt_dropout, self.w) + self.b) def cost(self, net): "   ." return -T.mean(T.log(self.output_dropout)[T.arange(net.y.shape[0]), net.y]) def accuracy(self, y): "  -." return T.mean(T.eq(y, self.y_out)) ####  def size(data): "    `data`." return data[0].get_value(borrow=True).shape[0] def dropout_layer(layer, p_dropout): srng = shared_randomstreams.RandomStreams( np.random.RandomState(0).randint(999999)) mask = srng.binomial(n=1, p=1-p_dropout, size=layer.shape) return layer*T.cast(mask, theano.config.floatX) 

Tugasnya

• SGD . , . network3.py , .
• Network , .
• SGD , η ( , , , ).
• , . network3.py, . , , . .
• .
• – . , , , ? .
• ReLU , ( -) . . , ReLU ( ). , c>0 c ^L−1 , L – . , softmax? ReLU? ? , , . , ReLU.
• . , ReLU? , ? : «» . – , - - .