Matematika Terpisah untuk WMS: Clustering Stock Lot

Artikel ini menjelaskan bagaimana, ketika memperkenalkan sistem WMS , kami dihadapkan dengan kebutuhan untuk menyelesaikan masalah pengelompokan non-standar dan dengan algoritma apa kami menyelesaikannya. Kami akan memberi tahu Anda bagaimana kami menerapkan pendekatan sistematis dan ilmiah untuk memecahkan masalah, kesulitan apa yang kami temui dan pelajaran apa yang kami pelajari.

Publikasi ini memulai serangkaian artikel yang kami bagikan pengalaman sukses kami dalam menerapkan algoritma pengoptimalan dalam proses gudang. Tujuan dari serangkaian artikel ini adalah untuk mengenalkan kepada khalayak dengan jenis-jenis tugas mengoptimalkan operasi gudang yang muncul di hampir semua gudang menengah dan besar, serta menceritakan pengalaman kami dalam memecahkan masalah-masalah seperti itu dan perangkap yang dijumpai di sepanjang jalan ini. Artikel-artikel akan berguna bagi mereka yang bekerja di industri logistik gudang, menerapkan sistem WMS , serta programmer yang tertarik pada aplikasi matematika dalam bisnis dan optimasi proses di perusahaan.

Proses bottleneck

Pada tahun 2018, kami membuat proyek untuk memperkenalkan sistem WMS di gudang perusahaan LD Trading House di Chelyabinsk. Memperkenalkan produk "1C-Logistik: Manajemen Gudang 3" untuk 20 pekerjaan: operator WMS , pemilik toko, pengemudi forklift. Gudang memiliki rata-rata sekitar 4 ribu m2, jumlah sel adalah 5.000 dan jumlah SKU 4500. Katup bola dari produksi kami sendiri dengan ukuran berbeda dari 1 kg hingga 400 kg disimpan di gudang. Persediaan di gudang disimpan dalam konteks bets karena kebutuhan untuk memilih barang sesuai dengan FIFO dan spesifik “in-line” penempatan produk (penjelasan di bawah).

Ketika merancang skema otomasi untuk proses gudang, kami dihadapkan dengan masalah penyimpanan stok yang tidak optimal. Penumpukan dan penyimpanan crane memiliki, seperti yang telah kita katakan, "baris" spesifik. Artinya, produk-produk dalam sel ditumpuk dalam satu baris di atas yang lain, dan kemampuan untuk meletakkan sepotong pada sepotong sering tidak ada (mereka jatuh, dan beratnya tidak kecil). Karena itu, ternyata hanya satu nomenklatur dari satu bets yang dapat berada dalam satu unit penyimpanan, jika tidak, nomenklatur lama tidak dapat ditarik keluar dari yang baru tanpa "menyekop" seluruh sel.

Produk tiba di gudang setiap hari dan setiap kedatangan adalah batch yang terpisah. Secara total, sebagai hasil dari operasi gudang selama 1 bulan, 30 lot terpisah dibuat, meskipun masing-masing harus disimpan dalam sel yang terpisah. Barang sering dipilih bukan dalam palet utuh, tetapi dalam potongan, dan sebagai hasilnya, di daerah pemilihan potongan, dalam banyak sel gambar berikut diamati: dalam sel dengan volume lebih dari 1 m3 ada beberapa potongan crane yang menempati kurang dari 5-10% volume sel (lihat Gambar 1). )

Gambar 1. Foto beberapa potong barang di dalam sel

Di muka penggunaan kapasitas penyimpanan yang kurang optimal. Untuk membayangkan skala bencana, saya dapat mengutip angka-angka: rata-rata ada antara 100 dan 300 sel seperti sel dengan sedikit sisa dalam periode yang berbeda dari operasi gudang. Karena gudang relatif kecil, pada musim pemuatan gudang faktor ini menjadi "leher sempit" dan sangat menghambat proses gudang.

Gagasan memecahkan masalah

Idenya muncul: untuk membawa kumpulan residu dengan tanggal terdekat ke satu batch tunggal dan menempatkan keseimbangan tersebut dengan batch terpadu secara kompak dalam satu sel, atau dalam beberapa jika tidak ada ruang yang cukup dalam satu untuk mengakomodasi jumlah total saldo.


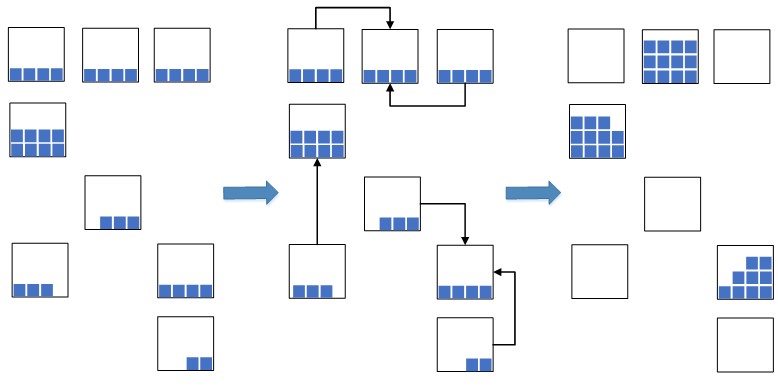Fig. 2. Skema kompresi sel

Ini memungkinkan Anda untuk secara signifikan mengurangi ruang gudang yang ditempati, yang akan digunakan untuk barang yang baru ditempatkan. Dalam situasi dengan kapasitas gudang yang berlebihan, langkah seperti itu sangat diperlukan, jika tidak, mungkin tidak ada cukup ruang kosong untuk penempatan barang baru, yang akan menyebabkan penghenti dalam proses penempatan dan pengisian gudang. Sebelumnya, sebelum implementasi sistem WMS- , operasi seperti itu dilakukan secara manual, yang tidak efektif, karena proses menemukan residu yang sesuai dalam sel cukup lama. Sekarang, dengan diperkenalkannya sistem WMS, mereka memutuskan untuk mengotomatiskan proses, mempercepatnya dan membuatnya cerdas.

Proses pemecahan masalah ini dibagi menjadi 2 tahap:

• pada tahap pertama, kami menemukan kelompok-kelompok pihak yang tutup tanggal untuk kompresi;
• pada tahap kedua, untuk setiap kelompok batch kami menghitung penempatan residu produk yang paling kompak dalam sel.

Pada artikel saat ini, kami akan fokus pada tahap pertama algoritma, dan meninggalkan cakupan tahap kedua untuk artikel selanjutnya.

Cari model matematika dari suatu masalah

Sebelum kita duduk untuk menulis kode dan menemukan sepeda kita, kita memutuskan untuk mendekati masalah ini secara ilmiah, yaitu: merumuskannya secara matematis, menguranginya menjadi masalah optimalisasi diskrit yang terkenal dan menggunakan algoritma yang ada yang efektif untuk menyelesaikannya, atau mengambil algoritma yang ada ini sebagai dasar dan memodifikasinya di bawah spesifik tugas praktis yang harus diselesaikan.

Karena jelas mengikuti dari pernyataan bisnis masalah yang kita hadapi dengan set, kita merumuskan masalah seperti itu dalam hal teori set.

Biarkan $$$P$ - set semua banyak sisa-sisa beberapa barang dalam persediaan. Biarkan $$$C$ - konstanta hari yang diberikan. Biarkan $$$K$ - subset batch di mana perbedaan tanggal untuk semua pasangan batch dari subset tidak melebihi konstanta $$$C$ . Temukan jumlah minimum subset yang terpisah $$$K$ sedemikian rupa sehingga semua himpunan bagian $$$K$ secara kolektif akan memberi banyak $$$P$ .

Selain itu, kita perlu menemukan tidak hanya jumlah minimum himpunan bagian, tetapi sehingga himpunan bagian tersebut akan sebesar mungkin. Ini disebabkan oleh fakta bahwa setelah pengelompokan bets, kami akan "mengompres" sisa-sisa bets yang ditemukan dalam sel. Mari kita ilustrasikan dengan sebuah contoh. Misalkan ada banyak pihak yang terdistribusi pada sumbu waktu, seperti pada Gambar 3.
Fig. 3. Opsi Pemisahan Banyak

Dari dua opsi untuk memisahkan set P dengan jumlah himpunan bagian yang sama, partisi pertama (a) paling bermanfaat untuk tugas kita. Karena, semakin banyak pihak dalam grup, semakin banyak kombinasi kompresi yang muncul, dan dengan demikian semakin besar kemungkinan untuk menemukan kompresi yang paling kompak. Tentu saja, aturan seperti itu tidak lebih dari heuristik dan asumsi spekulatif kita. Meskipun, seperti yang diperlihatkan percobaan komputasi, jika kondisi maksimalisasi diperhitungkan, kekompakan kompresi residu selanjutnya menjadi rata-rata 5-10% lebih tinggi daripada kompresi yang dibangun tanpa memperhitungkan kondisi seperti itu.

Dengan kata lain, singkatnya, kita perlu menemukan kelompok atau kelompok pihak yang serupa di mana kriteria kesamaan ditentukan oleh konstanta $$$C$ . Tugas ini mengingatkan kita pada masalah pengelompokan yang terkenal. Penting untuk mengatakan bahwa masalah yang dipertimbangkan berbeda dari masalah pengelompokan dalam bahwa dalam masalah kami ada kondisi yang didefinisikan secara ketat untuk kriteria kesamaan elemen-elemen kluster, yang ditentukan oleh konstanta $$$C$ , dan dalam masalah pengelompokan tidak ada kondisi seperti itu. Pernyataan masalah pengelompokan dan informasi tentang tugas ini dapat ditemukan di sini.

Jadi, kami berhasil merumuskan masalah dan menemukan masalah klasik dengan formulasi serupa. Sekarang Anda perlu mempertimbangkan algoritma terkenal untuk menyelesaikannya, agar tidak menemukan kembali roda, tetapi untuk mengambil praktik terbaik dan menerapkannya. Untuk mengatasi masalah pengelompokan, kami mempertimbangkan algoritma yang paling populer, yaitu: $$$k$ -berarti $$$c$ -berarti, algoritma untuk memilih komponen yang terhubung, algoritma spanning tree minimal. Deskripsi dan analisis algoritma semacam itu dapat ditemukan di sini.

Untuk mengatasi masalah kami, algoritma pengelompokan $$$k$ -berarti dan $$$c$ -berarti tidak berlaku sama sekali, karena jumlah cluster tidak pernah diketahui sebelumnya $$$k$ dan algoritma seperti itu tidak memperhitungkan pembatasan konstanta hari. Algoritma tersebut pada awalnya dibuang.
Untuk mengatasi masalah kami, algoritma untuk memilih komponen yang terhubung dan algoritma spanning tree minimum lebih cocok, tetapi ternyata tidak dapat diterapkan secara langsung pada masalah yang sedang dipecahkan dan mendapatkan solusi yang baik. Untuk memperjelas hal ini, kami mempertimbangkan logika pengoperasian algoritma seperti yang diterapkan pada masalah kami.

Pertimbangkan grafiknya $$$G$ di mana puncaknya banyak pihak $$$P$ , dan tepi antara simpul $$$p_1$ dan $$$p_2$ memiliki berat yang sama dengan perbedaan hari antara batch $$$p_1$ dan $$$p_2$ . Dalam algoritma untuk memilih komponen yang terhubung, parameter input ditentukan $$$R$ dimana $$$R \ leq C$ , dan dalam grafik $$$G$ semua tepi yang beratnya dihilangkan dihapus $$$R$ . Hanya pasangan benda terdekat yang tetap terhubung. Arti dari algoritma ini adalah untuk memilih nilai seperti itu $$$R$ , di mana grafik "terpecah-pecah" menjadi beberapa komponen yang terhubung, di mana pihak-pihak yang termasuk dalam komponen ini memenuhi kriteria kesamaan kami, yang ditentukan oleh konstanta $$$C$ . Komponen yang dihasilkan adalah cluster.

Algoritma spanning tree minimum pertama kali dibangun di atas grafik $$$G$ minimum spanning tree, dan kemudian secara berurutan menghilangkan ujung-ujungnya dengan bobot terbesar hingga grafik “pecah” menjadi beberapa komponen yang terhubung, di mana lot yang dimiliki komponen ini juga akan memenuhi kriteria kesamaan kami. Komponen yang dihasilkan adalah cluster.

Ketika menggunakan algoritme tersebut untuk menyelesaikan masalah yang sedang dipertimbangkan, sebuah situasi dapat muncul seperti pada Gambar 4.


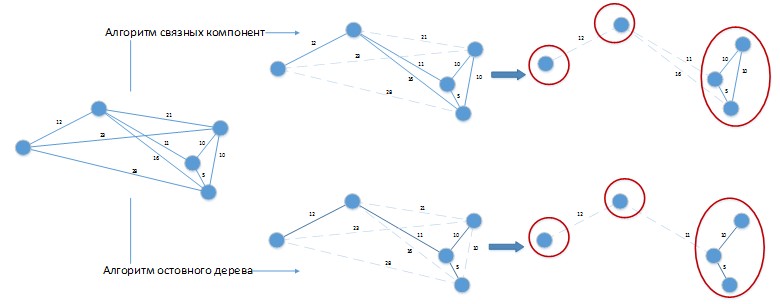Gambar 4. Aplikasi algoritma pengelompokan untuk masalah yang sedang dipecahkan.

Misalkan kita memiliki perbedaan konstan dari hari-hari para pihak adalah 20 hari. Hitung $$$G$ digambarkan dalam bentuk spasial untuk kenyamanan persepsi visual. Kedua algoritma memberikan solusi dengan 3 cluster, yang dapat dengan mudah ditingkatkan dengan menggabungkan batch yang ditempatkan di cluster terpisah di antara mereka! Jelas, algoritma tersebut perlu dikembangkan lebih lanjut sesuai dengan spesifik masalah yang sedang dipecahkan dan aplikasi murni mereka untuk solusi masalah kita akan memberikan hasil yang buruk.


Jadi, sebelum mulai menulis kode algoritme grafik yang dimodifikasi untuk tugas kami dan menciptakan sepeda kami sendiri (di mana siluet garis-garis roda persegi sudah dapat ditebak), kami kembali memutuskan untuk mendekati masalah ini secara ilmiah, yaitu: mencoba menguranginya menjadi masalah diskrit lain. optimisasi, dengan harapan bahwa algoritma yang ada untuk solusinya dapat diterapkan tanpa modifikasi.

Pencarian berikutnya untuk masalah klasik serupa berhasil! Itu mungkin untuk menemukan masalah optimasi diskrit, pernyataan yang hampir 1 dalam 1 bertepatan dengan pernyataan masalah kita. Masalah ini ternyata menjadi masalah menutupi set . Kami menyajikan pernyataan masalah sebagaimana diterapkan pada spesifikasi kami.

Ada satu set yang terbatas $$$P$ dan keluarga $$$S$ dari semua subset pihak yang terpisah, sehingga perbedaan tanggal untuk semua pasangan partai dari setiap subset $$$I$ dari keluarga $$$S$ tidak melebihi konstanta $$$C$ . Pelapisan disebut keluarga $$$U$ Setidaknya kekuatan yang elemennya termasuk $$$S$ sedemikian rupa sehingga persatuan set $$$I$ dari keluarga $$$U$ harus memberikan banyak dari semua pihak $$$P$ .

Analisis terperinci tentang masalah ini dapat ditemukan di sini dan di sini. Pilihan lain untuk aplikasi praktis masalah cakupan dan modifikasinya dapat ditemukan di sini.

Satu-satunya perbedaan kecil antara masalah yang dipertimbangkan dan masalah klasik yang meliputi suatu himpunan adalah kebutuhan untuk memaksimalkan jumlah elemen dalam himpunan bagian. Tentu saja, orang dapat mencari artikel di mana kasus khusus dipertimbangkan dan, kemungkinan besar, mereka akan ditemukan. Tetapi, dari pencarian artikel selanjutnya, kami terselamatkan oleh fakta bahwa algoritma "serakah" yang terkenal untuk memecahkan masalah klasik dalam peliputan set membangun partisi hanya dengan mempertimbangkan maksimalisasi jumlah elemen dalam himpunan bagian. Jadi, kami berlari sedikit ke depan, dan sekarang semuanya beres.

Algoritma untuk memecahkan masalah

Kami telah memutuskan pada model matematika masalah yang harus dipecahkan. Sekarang kita mulai mempertimbangkan algoritma untuk solusinya. Subset $$$I$ dari keluarga $$$S$ dapat dengan mudah ditemukan, misalnya, dengan prosedur seperti itu.

1. Langkah 0. Atur kumpulan dari set $$$P$ dalam urutan tanggal mereka. Kami percaya bahwa semua pihak tidak ditandai sebagai dilihat.
2. Langkah 1. Temukan pesta dengan tanggal terkecil dari para pihak yang belum dilihat.
3. Langkah 2. Untuk pihak yang ditemukan, bergerak ke kanan, kami sertakan dalam subset $$$I$ semua pihak yang tanggalnya berbeda dari tanggal saat ini tidak lebih dari $$$C$ hari. Semua batch termasuk dalam set $$$I$ tandai seperti yang dilihat.
4. Langkah 3. Jika, ketika bergerak ke kanan, kumpulan berikutnya tidak dapat dimasukkan $$$I$ , lalu lanjutkan ke langkah 1.

Masalah menutupi satu set adalah $$$NP$ - sulit, yang berarti bahwa untuk solusinya tidak ada yang cepat (dengan waktu operasi sama dengan polinomial dari data input) dan algoritma yang akurat. Oleh karena itu, untuk memecahkan masalah meliputi himpunan, dipilih algoritma serakah cepat, yang tentu saja tidak tepat, tetapi memiliki keuntungan sebagai berikut:

• Untuk masalah dimensi kecil (dan ini hanya kasus kami), ini menghitung solusi yang cukup dekat ke optimal. Ketika ukuran masalah bertambah, kualitas larutan memburuk, tetapi masih agak lambat;
• Sangat mudah diimplementasikan;
• Cepat, karena perkiraan waktu operasinya adalah $$$O (mn)$ .

Algoritma serakah memilih set yang dipandu oleh aturan berikut: pada setiap tahap, set dipilih yang mencakup jumlah maksimum elemen yang belum tercakup. Penjelasan terperinci dari algoritma dan pseudo-code-nya dapat ditemukan di sini. Implementasi algoritma dalam bahasa 1C dalam spoiler lebih rendah (tentang mengapa mereka mulai mengimplementasikannya dalam bahasa "kuning" pada bab berikutnya).


Tentu saja, optimalitas dari algoritma semacam itu tidak mungkin - heuristik, untuk mengatakan apa-apa. Anda dapat menemukan contoh seperti itu di mana algoritma seperti itu salah. Kesalahan semacam itu muncul ketika, pada beberapa iterasi, kami menemukan beberapa set dengan jumlah elemen yang sama dan memilih elemen pertama yang muncul, karena strateginya serakah: Saya mengambil hal pertama yang menarik perhatian saya dan "serakah" puas.

Mungkin saja pilihan semacam itu dapat mengarah pada hasil suboptimal pada iterasi selanjutnya. Tetapi akurasi dari algoritma yang sederhana masih cukup bagus dalam banyak kasus. Jika Anda ingin mendapatkan solusi untuk masalah lebih akurat, maka Anda perlu menggunakan algoritma yang lebih kompleks, misalnya, seperti dalam pekerjaan : algoritma serakah probabilistik, algoritma koloni semut, dll. Hasil membandingkan algoritma tersebut pada data acak yang dihasilkan dapat ditemukan dalam pekerjaan.

Implementasi dan implementasi algoritma

Algoritme seperti itu diimplementasikan dalam bahasa 1C dan dimasukkan dalam pemrosesan eksternal yang disebut "Kompresi residu", yang terhubung ke sistem WMS . Kami tidak menerapkan algoritme dalam C ++ dan menggunakannya dari komponen Native eksternal, yang akan lebih benar, karena kecepatan kode C ++ beberapa kali dan dalam beberapa contoh bahkan sepuluh kali lebih cepat daripada kecepatan kode serupa di 1C . Di 1C, algoritma ini diterapkan untuk menghemat waktu pengembangan dan kemudahan debugging di pangkalan kerja pelanggan. Hasil algoritma ditunjukkan pada Gambar 6.


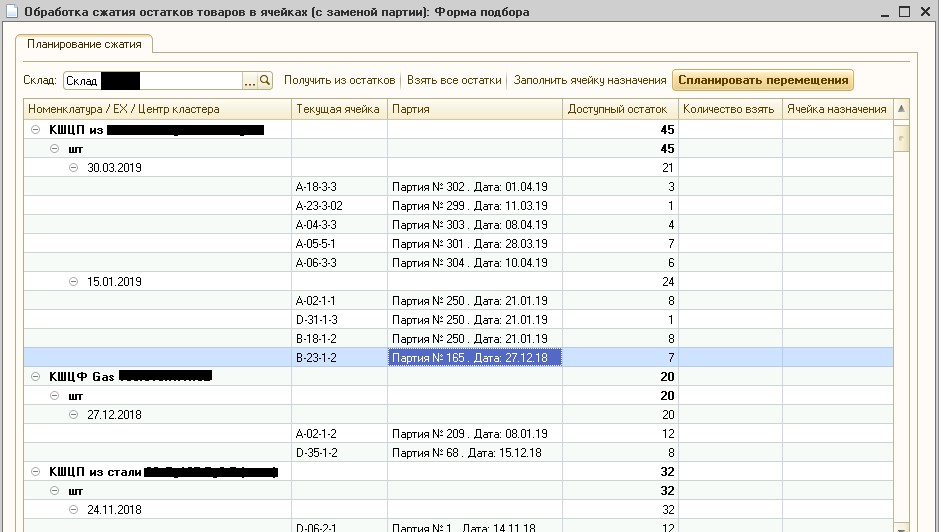Fig. 6. Pemrosesan Kompresi Residu

Gambar 6 menunjukkan bahwa di gudang yang ditunjukkan stok barang saat ini dalam sel penyimpanan dibagi menjadi beberapa kelompok, di mana tanggal pengiriman berbeda dengan tidak lebih dari 30 hari. Karena pelanggan memproduksi dan menyimpan katup bola logam dengan umur simpan bertahun-tahun, perbedaan tanggal ini dapat diabaikan. Perhatikan bahwa saat ini pemrosesan tersebut digunakan dalam produksi secara sistematis, dan operator WMS mengkonfirmasi kualitas batch yang baik.

Kesimpulan dan lanjutan

Pengalaman utama yang kami peroleh dari penyelesaian masalah praktis seperti itu adalah untuk mengkonfirmasi keefektifan penggunaan paradigma: Mat. pernyataan tugas $$$\ rightarrow$ tikar terkenal. model $$$\ rightarrow$ algoritma terkenal $$$\ rightarrow$ algoritma dengan mempertimbangkan spesifikasi tugas. Sudah ada lebih dari 300 tahun optimasi diskrit dan selama waktu ini orang berhasil mempertimbangkan banyak masalah dan mendapatkan banyak pengalaman dalam menyelesaikannya. Pertama-tama, lebih disarankan untuk beralih ke pengalaman ini, dan baru kemudian mulai menciptakan kembali sepeda Anda.

Penting juga untuk mengatakan bahwa solusi untuk masalah pengelompokan dapat dianggap tidak terpisah dari solusi untuk masalah mengompresi sisa batch, tetapi untuk menyelesaikan masalah tersebut bersama-sama. Yaitu, untuk memilih partisi partai seperti itu ke dalam kelompok yang akan memberikan kompresi terbaik. Tetapi solusi untuk masalah seperti itu diputuskan untuk dibagi karena alasan-alasan berikut:

• Anggaran terbatas untuk pengembangan algoritma. Pengembangan seperti umum, dan karenanya algoritma yang lebih kompleks akan lebih memakan waktu.
• Kompleksitas debugging dan pengujian. Algoritma umum akan lebih sulit untuk menguji dan debug pada tahap penerimaan, dan bug di dalamnya akan lebih sulit dan lebih lama untuk debug dalam operasi real-time. Misalnya, kesalahan terjadi dan tidak jelas di mana untuk menggali: kempa atap menuju pengelompokan, atap kempa menuju kompresi?
• Transparansi dan pengelolaan. Pemisahan kedua tugas membuat proses kompresi lebih transparan, dan karenanya lebih mudah dikelola bagi pengguna akhir - operator WMS. Mereka dapat menghapus beberapa sel dari kompresi atau mengedit kuantitas kompresibel untuk beberapa alasan.

Pada artikel berikutnya, kami akan melanjutkan diskusi tentang algoritma optimasi dan mempertimbangkan yang paling menarik dan jauh lebih kompleks: algoritma optimal untuk "kompresi" residu dalam sel, yang menggunakan input yang diterima dari algoritma pengelompokan batch sebagai input.

Mempersiapkan artikel
Roman Shangin, Programmer, Departemen Proyek,
Perusahaan BIT pertama, Chelyabinsk