☝🏾 👩 👩🏼‍✈️ Matematika diskrit untuk WMS: algoritma untuk mengompresi barang dalam sel (bagian 2) 🕵️ 💸 ⛺️

Dalam artikel ini, kami akan menjelaskan bagaimana kami mengembangkan algoritma untuk kompresi optimal dari barang yang tersisa dalam sel. Kami akan memberi tahu Anda bagaimana memilih metaheuristik yang diperlukan dari lingkungan kerangka kebun binatang: pencarian tabu, algoritma genetika, koloni semut, dll.

Kami akan melakukan percobaan komputasi untuk menganalisis waktu operasi dan keakuratan algoritma. Kami merangkum dan merangkum pengalaman berharga yang diperoleh dalam menyelesaikan masalah optimisasi dan implementasi "teknologi cerdas" ini dalam proses bisnis pelanggan.

Artikel ini akan berguna bagi mereka yang menerapkan teknologi cerdas, bekerja di gudang atau industri logistik produksi, serta programmer yang tertarik pada aplikasi matematika dalam bisnis dan optimalisasi proses di perusahaan.

Bagian pengantar

Publikasi ini melanjutkan serangkaian artikel yang kami bagikan pengalaman sukses kami dalam menerapkan algoritma pengoptimalan dalam proses gudang. Publikasi sebelumnya:

Cara membaca artikel. Jika Anda membaca artikel sebelumnya, Anda dapat langsung melanjutkan ke bab "Pengembangan algoritma untuk menyelesaikan masalah", jika tidak, maka uraian masalah yang harus dipecahkan dalam spoiler di bawah ini.

Deskripsi masalah yang harus dipecahkan di gudang pelanggan

Proses bottleneck

Pada tahun 2018, kami membuat proyek untuk memperkenalkan sistem WMS di gudang perusahaan LD Trading House di Chelyabinsk. Memperkenalkan produk "1C-Logistik: Manajemen Gudang 3" untuk 20 pekerjaan: operator WMS , pemilik toko, pengemudi forklift. Gudang memiliki rata-rata sekitar 4 ribu m2, jumlah sel adalah 5.000 dan jumlah SKU 4500. Katup bola dari produksi kami sendiri dengan ukuran berbeda dari 1 kg hingga 400 kg disimpan di gudang. Persediaan di gudang disimpan dalam konteks bets karena kebutuhan untuk memilih barang sesuai dengan FIFO dan spesifik “in-line” penempatan produk (penjelasan di bawah).

Ketika merancang skema otomasi untuk proses gudang, kami dihadapkan dengan masalah penyimpanan stok yang tidak optimal. Penumpukan dan penyimpanan crane memiliki, seperti yang telah kita katakan, "baris" spesifik. Artinya, produk-produk dalam sel ditumpuk dalam satu baris di atas yang lain, dan kemampuan untuk meletakkan sepotong pada sepotong sering tidak ada (mereka jatuh, dan beratnya tidak kecil). Karena itu, ternyata hanya satu nomenklatur dari satu bets yang dapat berada dalam satu unit penyimpanan, jika tidak, nomenklatur lama tidak dapat ditarik keluar dari yang baru tanpa "menyekop" seluruh sel.

Produk tiba di gudang setiap hari dan setiap kedatangan adalah batch yang terpisah. Secara total, sebagai hasil dari operasi gudang selama 1 bulan, 30 lot terpisah dibuat, meskipun masing-masing harus disimpan dalam sel yang terpisah. Barang sering dipilih bukan dalam palet utuh, tetapi dalam potongan, dan sebagai hasilnya, di daerah pemilihan potongan, dalam banyak sel gambar berikut diamati: dalam sel dengan volume lebih dari 1 m3 ada beberapa potongan crane yang menempati kurang dari 5-10% volume sel (lihat Gambar 1). )

Gambar 1. Foto beberapa potong dalam sel

Di muka penggunaan kapasitas penyimpanan yang kurang optimal. Untuk membayangkan skala bencana, saya dapat mengutip angka-angka: rata-rata ada antara 100 dan 300 sel seperti sel dengan sedikit sisa dalam periode yang berbeda dari operasi gudang. Karena gudang relatif kecil, pada musim pemuatan gudang faktor ini menjadi "leher sempit" dan sangat menghambat proses penerimaan dan pengiriman gudang.

Gagasan memecahkan masalah

Idenya muncul: untuk membawa kumpulan residu dengan tanggal terdekat ke satu batch tunggal dan menempatkan keseimbangan tersebut dengan batch terpadu secara kompak dalam satu sel, atau dalam beberapa jika tidak ada ruang yang cukup dalam satu untuk mengakomodasi jumlah total saldo. Contoh "kompresi" seperti itu ditunjukkan pada Gambar 2.

Fig. 2. Skema kompresi sel

Ini memungkinkan Anda untuk secara signifikan mengurangi ruang gudang yang ditempati, yang akan digunakan untuk barang yang baru ditempatkan. Dalam situasi kelebihan kapasitas gudang, langkah seperti itu sangat diperlukan, jika tidak mungkin tidak ada cukup ruang kosong untuk menempatkan barang baru, yang akan menyebabkan penghenti dalam proses penempatan dan pengisian gudang, dan sebagai akibatnya, penghenti untuk penerimaan dan pengiriman. Sebelumnya, sebelum implementasi sistem WMS, operasi seperti itu dilakukan secara manual, yang tidak efektif, karena proses menemukan residu yang sesuai dalam sel cukup lama. Sekarang, dengan diperkenalkannya sistem WMS, mereka memutuskan untuk mengotomatiskan proses, mempercepatnya dan membuatnya cerdas.

Proses pemecahan masalah ini dibagi menjadi 2 tahap:

pada tahap pertama, kami menemukan kelompok-kelompok pihak yang tanggal dekat untuk dikompres (ini adalah artikel pertama untuk tugas penahbisan ini);
pada tahap kedua, untuk setiap kelompok batch kami menghitung penempatan residu produk yang paling kompak dalam sel.

Pada artikel saat ini, kita selesai dengan deskripsi tahap kedua dari proses solusi dan langsung mempertimbangkan algoritma optimasi itu sendiri.

Pengembangan suatu algoritma untuk memecahkan masalah

Sebelum melanjutkan dengan deskripsi langsung dari algoritma optimasi, perlu untuk mengatakan tentang kriteria utama untuk pengembangan algoritma seperti itu, yang ditetapkan sebagai bagian dari proyek implementasi sistem WMS .

Pertama, algoritme harus mudah dipahami . Ini adalah persyaratan alami, karena diasumsikan bahwa algoritma akan didukung dan dikembangkan lebih lanjut oleh layanan TI pelanggan di masa depan, yang seringkali jauh dari kehalusan dan kebijaksanaan matematis.
Kedua, algoritme harus cepat . Hampir semua barang di gudang terlibat dalam prosedur kompresi (ini adalah sekitar 3.000 item) dan untuk setiap produk perlu untuk menyelesaikan masalah dimensi sekitar 10x100.
Ketiga, algoritma harus menghitung solusi yang mendekati optimal .
Keempat, waktu untuk mendesain, mengimplementasikan, men-debug, menganalisis dan menguji internal algoritma relatif kecil. Ini merupakan persyaratan penting, karena anggaran proyek , termasuk untuk tugas ini, terbatas .

Perlu dikatakan bahwa sampai saat ini, matematikawan telah mengembangkan banyak algoritma yang efektif untuk menyelesaikan masalah Masalah Lokasi Fasilitas Sumber Tunggal. Pertimbangkan varietas utama dari algoritma yang tersedia.

Beberapa algoritma yang paling efisien didasarkan pada pendekatan yang disebut relaksasi Lagrange. Sebagai aturan, ini adalah algoritma yang agak rumit yang sulit dipahami bagi seseorang yang tidak tenggelam dalam seluk-beluk optimasi diskrit. “Kotak hitam” dengan algoritma kompleks Lagrange yang efektif namun tidak sesuai untuk pelanggan.

Ada metaheuristik yang cukup efektif (apa yang dibaca metaheuristik di sini , apa heuristik baca di sini ), misalnya, algoritma genetika, algoritma annealing disimulasikan, algoritma koloni semut, algoritma pencarian Tabu dan lain-lain (gambaran metaheuristik seperti itu dalam bahasa Rusia dapat ditemukan di sini ). Tetapi algoritma tersebut telah memuaskan pelanggan, karena:

Mampu menghitung solusi untuk masalah yang sangat dekat dengan optimal.
Cukup sederhana untuk dipahami, dukungan lebih lanjut, debug dan perbaiki.
Mereka dapat dengan cepat menghitung solusi untuk suatu masalah.

Diputuskan untuk menggunakan metaheuristik. Sekarang tinggal memilih satu "kerangka kerja" di antara "kebun binatang" besar metaheuristik terkenal untuk menyelesaikan Masalah Lokasi Fasilitas Fasilitas Sumber Tunggal. Setelah meninjau sejumlah artikel yang menganalisis efektivitas berbagai metaheuristik, pilihan kami jatuh pada algoritma GRASP, karena dibandingkan dengan metaheuristik lainnya itu menunjukkan hasil yang cukup baik pada keakuratan solusi yang dihitung untuk masalah, adalah salah satu yang tercepat dan, yang paling penting, ia memiliki yang paling sederhana dan paling sederhana. dan logika transparan.

Skema algoritma GRASP dalam kaitannya dengan tugas Masalah Lokasi Fasilitas Berkapasitas Sumber Tunggal dijelaskan secara rinci dalam artikel . Skema umum dari algoritma adalah sebagai berikut.

Tahap 1. Hasilkan beberapa solusi yang layak untuk masalah dengan algoritma acak serakah.
Tahap 2. Tingkatkan solusi yang dihasilkan di tahap 1 menggunakan algoritma pencarian lokal di sejumlah lingkungan.
Jika kondisi berhenti terpenuhi, maka selesaikan algoritme, jika tidak, lanjutkan ke langkah 1. Solusi dengan biaya total terendah di antara semua solusi yang ditemukan adalah hasil dari algoritma.

Kondisi untuk menghentikan algoritma dapat berupa batasan sederhana pada jumlah iterasi atau batasan pada jumlah iterasi tanpa perbaikan dalam solusi.

Kode skema umum dari algoritma

int computeProblemSolution(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolution, int **aMatAssignmentSolution) { //       //  int     .      WMS   3  ( .,    10 ),         // aMatSolutionIteration -    : // [i][0]  , [i][1]     , [i][2]             // [i][3]        int **aMatSolutionIteration = new int*[cellsNumb]; for (int count = 0; count < cellsNumb; count++) aMatSolutionIteration[count] = new int[4]; // aMatAssignmentSolutionIteration -     . [i][j] = 1 -  j   i, 0    int **aMatAssignmentSolutionIteration = new int*[cellsNumb]; for (int count = 0; count < cellsNumb; count++) aMatAssignmentSolutionIteration[count] = new int[cellsNumb]; const int maxIteration = 10; int iter = 0, recordCosts = 1000000; //    ,      int totalDemand = 0; for (int i = 0; i < cellsNumb; i++) totalDemand += aCellsData[i][1]; while (iter < maxIteration) { //     setValueIn2Array(aMatAssignmentSolutionIteration, cellsNumb, cellsNumb, 0); //    setClearSolutionArray(aMatSolutionIteration, cellsNumb, 4); //      int *aFreeContainersFitnessFunction = new int[cellsNumb]; //   ,       findGreedyRandomSolution(aCellsData, aMatDist, cellsNumb, aMatSolutionIteration, aMatAssignmentSolutionIteration, aFreeContainersFitnessFunction, false); //         improveSolutionLocalSearch(aCellsData, aMatDist, cellsNumb, aMatSolutionIteration, aMatAssignmentSolutionIteration, totalDemand); //     (      ) bool feasible = isSolutionFeasible(aMatSolutionIteration, aCellsData, cellsNumb); //    ,    if (feasible == false) { getFeasibleSolution(aCellsData, aMatDist, cellsNumb, aMatSolutionIteration, aMatAssignmentSolutionIteration); } //        ,  ,          int totalCostsIteration = getSolutionTotalCosts(aMatSolutionIteration, cellsNumb); if (totalCostsIteration < recordCosts) { recordCosts = totalCostsIteration; copy2Array(aMatSolution, aMatSolutionIteration, cellsNumb, 3); } iter++; } delete2Array(aMatSolutionIteration, cellsNumb); delete2Array(aMatAssignmentSolutionIteration, cellsNumb); return recordCosts; }

Mari kita pertimbangkan lebih detail pengoperasian algoritma acak serakah pada tahap 1. Dipercayai bahwa pada awalnya tidak satu sel-kontainer dipilih.

Langkah 1. Untuk setiap sel kontainer yang saat ini tidak dipilih, nilainya dihitung $F_ {i} ^ {'}$ rumus biaya
$F_ {i} ^ {'} = \ frac {F_ {i}} {N},$
dimana $F_ {i} ^ {'}$ - jumlah biaya memilih wadah $i$ dan total biaya untuk memindahkan barang dari $N$ sel-sel yang belum melekat pada wadah apa pun ke dalam wadah $i$ . Seperti itu $N$ sel dipilih sehingga total volume barang di dalamnya tidak melebihi kapasitas wadah $i$ . Sel-sel donor dipilih secara berurutan untuk dipindahkan ke wadah $i$ dalam rangka meningkatkan biaya memindahkan jumlah barang ke dalam wadah $i$ . Pemilihan sel dilakukan sampai kapasitas wadah terlampaui.
Langkah 2. Set terbentuk $R$ wadah dengan nilai fungsi $F$ tidak melebihi nilai ambang batas $\ min (F) \ cdot (1 + a)$ dimana $a$ dalam kasus kami adalah 0,2.
Langkah 3. Secara acak dari set $R$ wadah dipilih $i$ . $N$ sel yang sebelumnya dipilih dalam wadah $i$ pada langkah 1, mereka akhirnya ditugaskan ke wadah seperti itu dan tidak berpartisipasi lebih lanjut dalam perhitungan algoritma serakah.
Langkah 4. Jika semua sel donor ditugaskan ke wadah, algoritma serakah berhenti bekerja, jika tidak kembali ke langkah 1.

Algoritma acak pada setiap iterasi mencoba untuk membangun solusi sedemikian rupa sehingga ada keseimbangan antara kualitas solusi yang dibangunnya, serta keanekaragamannya. Dua persyaratan ini untuk memulai keputusan adalah syarat utama untuk keberhasilan operasi algoritma, karena:

jika solusinya berkualitas buruk, maka peningkatan selanjutnya pada tahap 2 tidak akan menghasilkan hasil yang signifikan, karena bahkan memperbaiki solusi yang buruk, kami akan sangat sering mendapatkan solusi berkualitas buruk yang sama;
Jika semua solusi baik, tetapi sama, maka prosedur pencarian lokal akan menyatu dengan solusi yang sama, itu sama sekali bukan fakta yang optimal. Efek ini disebut memukul minimum lokal dan harus selalu dihindari.

Kode algoritma acak serakah

 void findGreedyRandomSolution(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolutionIteration, int **aMatAssignmentSolutionIteration, int *aFreeContainersFitnessFunction, bool isOldSolution) { //     int numCellsInSolution = 0; if (isOldSolution) { //     ,   aFreeContainersFitnessFunction //  numCellsInSolution ,       for (int i = 0; i < cellsNumb; i++) { for (int j = 0; j < cellsNumb; j++) { if (aMatAssignmentSolutionIteration[i][j] == 1) numCellsInSolution++; } } } //  ,        aFreeContainersFitnessFunction,     // [i][j] = 1,   j    i, 0  int **aFreeContainersAssigntCells = new int*[cellsNumb]; for (int count = 0; count < cellsNumb; count++) aFreeContainersAssigntCells[count] = new int[cellsNumb]; while (numCellsInSolution != cellsNumb) { setValueIn2Array(aFreeContainersAssigntCells, cellsNumb, cellsNumb, 0); //    //               setFreeContainersFitnessFunction(aCellsData, aMatDist, cellsNumb, aFreeContainersFitnessFunction, aFreeContainersAssigntCells); //   ,    //       ,          int selectedRandomContainer = selectGoodRandomContainer(aFreeContainersFitnessFunction, cellsNumb); //          aMatSolutionIteration[selectedRandomContainer][0] = selectedRandomContainer; aMatSolutionIteration[selectedRandomContainer][1] = 0; aMatSolutionIteration[selectedRandomContainer][2] = aCellsData[selectedRandomContainer][2]; for (int j = 0; j < cellsNumb; j++) { if (aFreeContainersAssigntCells[selectedRandomContainer][j] == 1) { aMatAssignmentSolutionIteration[selectedRandomContainer][j] = 1; aMatSolutionIteration[selectedRandomContainer][1] += aCellsData[j][1]; aMatSolutionIteration[selectedRandomContainer][2] += aMatDist[selectedRandomContainer][j]; aMatSolutionIteration[selectedRandomContainer][3] = 0; aFreeContainersFitnessFunction[j] = 10000; numCellsInSolution++; } } } delete2Array(aFreeContainersAssigntCells, cellsNumb); delete[] aFreeContainersFitnessFunction; } void setFreeContainersFitnessFunction(int **aCellsData, int **aMatDist, int cellsNumb, int *aFreeContainersFitnessFunction, int **aFreeContainersAssigntCells) { //  ,        i // [0][k] -      , [1][k] -   int **aCurrentDist = new int*[2]; for (int count = 0; count < 2; count++) aCurrentDist[count] = new int[cellsNumb]; for (int i = 0; i < cellsNumb; i++) { // 10000 -      ,        if (aFreeContainersFitnessFunction[i] >= 10000) continue; //       int containerCurrentVolume = aCellsData[i][1]; //      int containerCosts = aCellsData[i][2]; //  -,    i int amountAssignedCell = 0; setCurrentDist(aMatDist, cellsNumb, aCurrentDist, i); for (int j = 0; j < cellsNumb; j++) { int currentCell = aCurrentDist[1][j]; if (currentCell == i) continue; if (aFreeContainersFitnessFunction[currentCell] >= 10000) continue; if (aCellsData[i][0] < containerCurrentVolume + aCellsData[currentCell][1]) continue; aFreeContainersAssigntCells[i][currentCell] = 1; containerCosts += aCurrentDist[0][j]; containerCurrentVolume += aCellsData[currentCell][1]; amountAssignedCell++; } //           (     ) if (aCellsData[i][1] > 0) { aFreeContainersAssigntCells[i][i] = 1; amountAssignedCell++; } //       1 (     ),       //           1. //          .      ,     //     (   )            . //         (     ),        //   ,             . if (amountAssignedCell > 1) amountAssignedCell *= 10; if (amountAssignedCell > 0) aFreeContainersFitnessFunction[i] = containerCosts / amountAssignedCell; else aFreeContainersFitnessFunction[i] = 10000; } delete2Array(aCurrentDist, 2); } int selectGoodRandomContainer(int *aFreeContainersFitnessFunction, int cellsNumb) { int minFit = 10000; for (int i = 0; i < cellsNumb; i++) { if (minFit > aFreeContainersFitnessFunction[i]) minFit = aFreeContainersFitnessFunction[i]; } int threshold = minFit * (1.2); // 20 %      //       int *aFreeContainersThresholdFitnessFunction = new int[cellsNumb]; int containerNumber = 0; for (int i = 0; i < cellsNumb; i++) { if (threshold >= aFreeContainersFitnessFunction[i] && aFreeContainersFitnessFunction[i] < 10000) { aFreeContainersThresholdFitnessFunction[containerNumber] = i; containerNumber++; } } int randomNumber = rand() % containerNumber; int randomContainer = aFreeContainersThresholdFitnessFunction[randomNumber]; delete[] aFreeContainersThresholdFitnessFunction; return randomContainer; }

Setelah solusi "permulaan" dibangun pada tahap 1, algoritma dilanjutkan ke tahap 2, di mana peningkatan solusi yang ditemukan tersebut dilakukan, di mana peningkatan secara alami berarti mengurangi total biaya. Logika dari algoritma pencarian lokal pada langkah 2 adalah sebagai berikut.

Langkah 1. Untuk solusi saat ini $S$ semua solusi "tetangga" dibangun sesuai dengan beberapa jenis lingkungan $N1$ , $N2$ ... $N5$ dan untuk setiap solusi "tetangga", nilai total biaya dihitung.
Langkah 2. Jika di antara solusi tetangga ada solusi yang lebih baik $S1$ dari solusi aslinya $S$ lalu $S$ diasumsikan sama $S1$ dan algoritma melanjutkan ke langkah 1. Jika tidak, jika di antara solusi tetangga tidak ada solusi yang lebih baik daripada yang asli, maka tampilan lingkungan berubah ke yang baru yang belum dipertimbangkan sebelumnya, dan algoritma melanjutkan ke langkah 1. Jika semua pandangan yang tersedia dari lingkungan dipertimbangkan, tetapi gagal menemukan solusi yang lebih baik daripada yang asli, algoritma mengakhiri pekerjaannya.

Tampilan lingkungan dipilih secara berurutan dari tumpukan berikut:

$N1$ ,

$N2$ ,

$N3$ ,

$N4$ ,

$N5$ . Tampilan area sekitarnya dibagi menjadi 2 jenis: tipe pertama (lingkungan

$N1$ ,

$N2$ ,

$N3$ ), di mana banyak wadah tidak berubah, tetapi hanya opsi untuk melampirkan sel donor berubah; tipe kedua (lingkungan

$N4$ ,

$N5$ ), di mana tidak hanya opsi untuk menempelkan sel ke wadah berubah, tetapi juga banyak wadah itu sendiri.

Kami menunjukkan

$| J |$ - jumlah elemen dalam set

$J$ . Angka-angka di bawah ini menggambarkan opsi untuk jenis lingkungan pertama .

Fig. 7. Lingkungan

$N1$

Lingkungan

$N1$ (atau shift neighborhood): berisi semua opsi untuk menyelesaikan masalah yang berbeda dari aslinya dengan mengubah lampiran hanya satu sel donor ke wadah. Ukuran lingkungan tidak lebih

$| J |$ opsi.

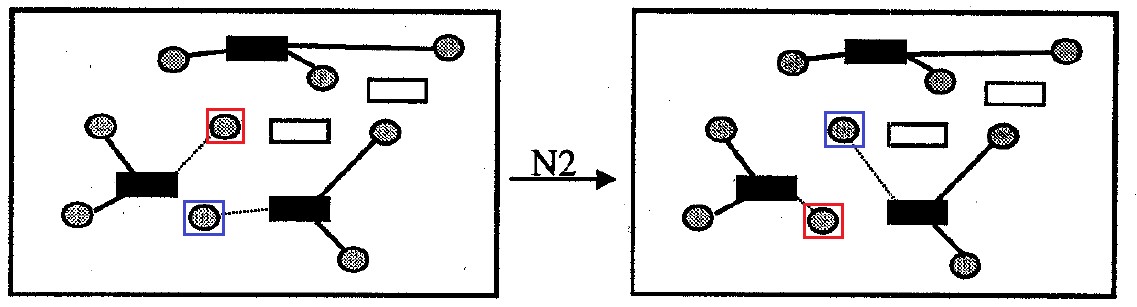Fig. 8. Lingkungan

$N2$

Kode algoritma pencarian lokal di lingkungan N1

 void findBestSolutionInNeighborhoodN1(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolutionIteration, int **aMatAssignmentSolutionIteration, int totalDemand, bool stayFeasible) { //        int recordDeltaCosts, recordCell, recordNewContainer, recordNewCosts, recordNewPenalty, recordOldContainer, recordOldCosts, recordOldPenalty; do { recordDeltaCosts = 10000; int totalContainersCapacity = 0; for (int i = 0; i < cellsNumb; i++) if (aMatSolutionIteration[i][1] > 0) totalContainersCapacity += aCellsData[i][0]; //   - for (int j = 0; j < cellsNumb; j++) { //   ,     j int currentContainer; for (int i = 0; i < cellsNumb; i++) { if (aMatAssignmentSolutionIteration[i][j] == 1) { currentContainer = i; break; } } //   ,     j (  ) int numbAssignedCells = 0; if (aMatSolutionIteration[j][0] >= 0) { for (int i = 0; i < cellsNumb; i++) { if (aMatAssignmentSolutionIteration[j][i] == 1) { numbAssignedCells = i; } } } else { numbAssignedCells = 0; } //    j        ,     j,       //     ""           ,     if (j == currentContainer && numbAssignedCells > 1) { continue; } //         int currentTotalContainersCapacity = totalContainersCapacity - aCellsData[currentContainer][0]; //  ,   ,        j    int currentCosts = aMatDist[currentContainer][j]; //        j         ,      if (aMatSolutionIteration[currentContainer][1] - aCellsData[j][1] == 0) currentCosts += aCellsData[currentContainer][2]; //        j        ,      int currentPenelty = getPenaltyValueForSingleCell(aCellsData, aMatSolutionIteration, currentContainer, j, 0); currentCosts += currentPenelty; for (int i = 0; i < cellsNumb; i++) { if (i == currentContainer) continue; if (stayFeasible) { if (max(0, aMatSolutionIteration[i][1]) + aCellsData[j][1] > aCellsData[i][0]) continue; } else { if (currentTotalContainersCapacity + aCellsData[i][0] < totalDemand) continue; } //     int newCosts = aMatDist[i][j]; //      if (aMatSolutionIteration[i][0] == -1) newCosts += aCellsData[i][2]; //        int newPenalty = getPenaltyValueForSingleCell(aCellsData, aMatSolutionIteration, i, j, 1); newCosts += newPenalty; int deltaCosts = newCosts - currentCosts; if (deltaCosts < 0 && deltaCosts < recordDeltaCosts) { recordDeltaCosts = deltaCosts; recordCell = j; recordNewContainer = i; recordNewCosts = newCosts; recordNewPenalty = newPenalty; recordOldContainer = currentContainer; recordOldCosts = currentCosts; recordOldPenalty = currentPenelty; } } } //   ,       if (recordDeltaCosts < 0) { //             aMatSolutionIteration[recordOldContainer][1] -= aCellsData[recordCell][1]; aMatSolutionIteration[recordOldContainer][2] -= recordOldCosts; if (aMatSolutionIteration[recordOldContainer][1] == 0) aMatSolutionIteration[recordOldContainer][0] = -1; aMatSolutionIteration[recordOldContainer][3] -= recordOldPenalty; aMatAssignmentSolutionIteration[recordOldContainer][recordCell] = 0; //             aMatSolutionIteration[recordNewContainer][1] += aCellsData[recordCell][1]; aMatSolutionIteration[recordNewContainer][2] += recordNewCosts; if (aMatSolutionIteration[recordNewContainer][0] == -1) aMatSolutionIteration[recordNewContainer][0] = recordNewContainer; aMatSolutionIteration[recordNewContainer][3] += recordNewPenalty; aMatAssignmentSolutionIteration[recordNewContainer][recordCell] = 1; //checkCorrectnessSolution(aCellsData, aMatDist, aMatAssignmentSolutionIteration, aMatSolutionIteration, cellsNumb); } } while (recordDeltaCosts < 0); }

Lingkungan

$N2$ (atau bertukar lingkungan): berisi semua opsi untuk menyelesaikan masalah yang berbeda dari yang asli dengan saling menukar lampiran ke wadah untuk sepasang sel donor. Ukuran lingkungan tidak lebih

$| J | ^ 2$ opsi.

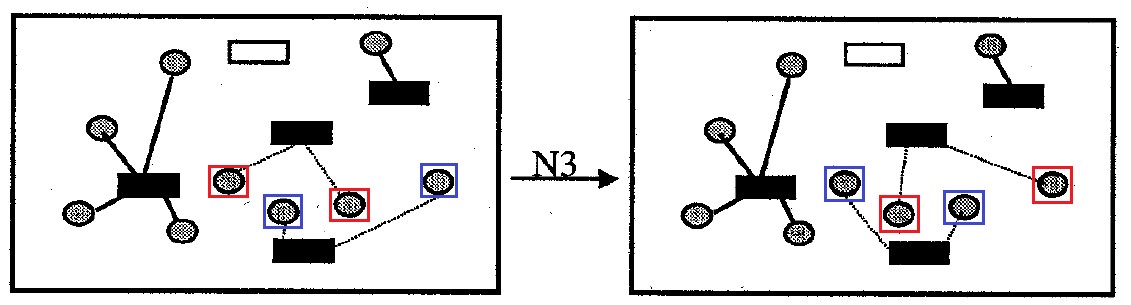Fig. 9. Lingkungan

$N3$

Lingkungan

$N3$ : berisi semua opsi untuk menyelesaikan masalah, yang berbeda dari yang asli dengan saling menggantikan lampiran semua sel untuk satu pasang wadah. Ukuran lingkungan tidak lebih

$| I |$ opsi.

Tipe kedua dari lingkungan dianggap sebagai mekanisme "diversifikasi" keputusan, ketika sudah tidak mungkin untuk mendapatkan perbaikan dengan mencari lingkungan "dekat" dari tipe pertama.

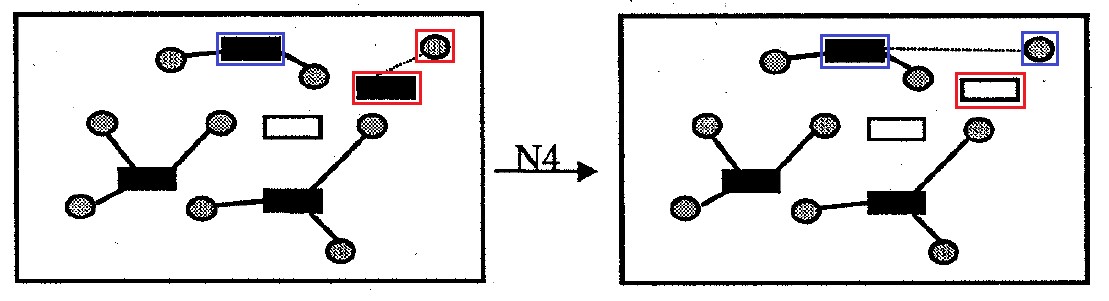Fig. 10. Lingkungan

$N4$

Lingkungan

$N4$ : berisi semua opsi untuk menyelesaikan masalah yang berbeda dari aslinya dengan menghapus satu sel wadah dari solusi. Sel-sel donor yang melekat pada wadah seperti itu yang dikeluarkan dari solusi melekat pada wadah lain untuk meminimalkan jumlah biaya transportasi dan penalti untuk melebihi kapasitas wadah. Ukuran lingkungan tidak lebih

$| I |$ opsi.

Fig. 11. Lingkungan sekitar

$N5$

Lingkungan

$N5$ : berisi semua opsi untuk menyelesaikan masalah yang berbeda dari yang asli dengan memisahkan sel dari satu wadah dan melampirkan sel tersebut ke wadah kosong lainnya untuk satu pasang wadah yang sewenang-wenang. Ukuran lingkungan tidak lebih

$| I | ^ 2$ opsi.

Para penulis artikel mengatakan bahwa, berdasarkan hasil eksperimen komputasi, pilihan terbaik adalah pertama-tama mencari lingkungan "dekat" dari jenis pertama, dan kemudian mencari lingkungan "jauh".

Perhatikan bahwa penulis artikel merekomendasikan melakukan pencarian di sekitarnya tanpa memperhitungkan batasan kapasitas masing-masing kontainer. Sebaliknya, jika kapasitas wadah terlampaui, maka tambahkan ke total biaya solusi sejumlah positif "baik", yang akan mengganggu daya tarik solusi seperti itu dibandingkan dengan solusi lain. Satu-satunya batasan ditempatkan pada total volume kontainer, yaitu total volume barang yang diangkut dari sel donor tidak boleh melebihi kapasitas total kontainer. Penghapusan pembatasan ini dilakukan karena jika pembatasan diperhitungkan, maka seringkali lingkungan tidak akan berisi solusi tunggal yang dapat diterima dan algoritma pencarian lokal akan menyelesaikan pekerjaannya segera setelah dimulai, tanpa melakukan perbaikan apa pun. Gambar 12 menunjukkan contoh operasi pencarian lokal tanpa memperhitungkan batasan kapasitas masing-masing kontainer.

Fig. 12. Pekerjaan pencarian lokal tanpa memperhitungkan batasan kapasitas masing-masing kontainer

Dalam gambar ini, diasumsikan bahwa residu merah dan hijau dari beberapa sel donor tidak menguntungkan untuk dipindahkan ke wadah lain kecuali yang kedua. Ini berarti bahwa perbaikan lebih lanjut dari solusi tidak mungkin, karena solusi baru yang layak untuk masalah, di mana pembatasan kapasitas dihormati, akan lebih buruk daripada yang asli dalam hal biaya transportasi. Seperti yang Anda lihat, algoritma untuk 2 iterasi membangun solusi yang layak jauh lebih baik daripada yang asli, meskipun fakta bahwa iterasi pertama membangun solusi yang tidak valid dengan kapasitas berlebih.

Perhatikan bahwa pendekatan ini memperkenalkan "penalti" untuk tidak dapat diterimanya solusi cukup umum dalam optimasi diskrit dan sering digunakan dalam algoritma seperti algoritma genetika, pencarian tabu, dll.

Setelah algoritma pencarian lokal selesai, jika solusi yang ditemukan masih tidak dapat diterima, yaitu, batas kapasitas kontainer telah dilampaui di suatu tempat, kami harus membawa solusi yang ditemukan ke bentuk yang dapat diterima, di mana semua pembatasan pada kapasitas kontainer dihormati. Algoritma untuk menyelesaikan tidak dapat diterimanya solusi adalah sebagai berikut.

Langkah 1. Lakukan pencarian lokal di lingkungan shift dan swap . Dalam hal ini, transisi hanya dilakukan dalam keputusan yang mengurangi jumlah "denda". Jika pengurangan penalti tidak memungkinkan, maka solusi dengan total biaya yang lebih rendah dipilih. Jika perbaikan lebih lanjut dengan pencarian lokal tidak mungkin dilakukan, lanjutkan ke langkah 2, jika tidak, jika solusi yang dihasilkan valid, maka selesaikan algoritme.
Langkah 2. Jika solusinya masih tidak dapat diterima, maka dari masing-masing wadah di mana terdapat kelebihan kapasitas, sel donor dilepaskan untuk meningkatkan volume barang hingga pembatasan kapasitas terpenuhi. Untuk sel-sel terpisah seperti itu, semua langkah dari algoritma, mulai dari yang pertama, diulangi, terlepas dari kenyataan bahwa set wadah yang tersedia tersedia dan cara untuk menempelkan sel-sel yang tersisa ke mereka tetap dan tidak dapat diubah. Perhatikan bahwa langkah 2 seperti itu, seperti yang diperlihatkan percobaan komputasi, harus dilakukan dengan sangat jarang.

Eksperimen komputasi dan analisis efisiensi algoritma

Algoritma GRASP diimplementasikan dari awal di C ++ , karena kami tidak menemukan kode sumber untuk algoritma yang dijelaskan dalam artikel . Kode program dikompilasi menggunakan g ++ dengan opsi optimasi -O2.

Kode proyek Visual Studio tersedia di GitHub . Satu-satunya hal yang diminta pelanggan adalah menghapus beberapa prosedur pencarian lokal paling kompleks untuk alasan kekayaan intelektual, rahasia dagang, dll.

Dalam artikel yang menggambarkan algoritma GRASP, efisiensi tinggi dinyatakan, di mana dengan efisiensi itu berarti bahwa itu secara stabil menghitung solusi yang sangat dekat dengan optimal, dan itu bekerja cukup cepat. Untuk memverifikasi keefektifan nyata dari algoritma GRASP seperti itu, kami melakukan eksperimen komputasi kami sendiri. Data input dari masalah dihasilkan oleh kami secara acak dengan distribusi yang seragam. Solusi yang dihitung oleh algoritma dibandingkan dengan solusi optimal, yang dihitung dengan algoritma yang tepat yang diusulkan dalam artikel . Sumber dari algoritma yang tepat seperti itu tersedia secara bebas di GitHub dengan referensi . Dimensi tugas, misalnya, 10x100 berarti kita memiliki 10 sel donor dan 100 sel wadah.

Perhitungan dilakukan pada komputer pribadi dengan karakteristik sebagai berikut: CPU 2.50 GHz, Intel Core i5-3210M, RAM 8 GB, sistem operasi Windows 10 (x64).

		GRASP	Rata-rata waktu berjalan dari algoritma yang tepat	Kesalahan rata-rata dari algoritma GRASP,%
5x50	50	0,08	1.22	0,2
10x50	50	0,14	3,75	0,4
10x100	50	0,55	15.81	1.4
10x200	25	2.21	82,73	1.8
20x100	25	1.06	264.15	2,3
20x200	25	4.21	797.39	2.7

Tabel 3. Perbandingan waktu operasi dari algoritma GRASP dan algoritma yang tepat

Seperti dapat dilihat dari tabel 3, algoritma GRASP benar-benar menghitung dekat dengan solusi optimal, dan dengan peningkatan dimensi masalah, kualitas solusi algoritma sedikit memburuk. Juga terlihat dari hasil percobaan bahwa algoritma GRASP cukup cepat, misalnya, ia memecahkan masalah dimensi 10x100 rata-rata dalam 0,5 detik. Perlu disebutkan pada akhirnya bahwa hasil percobaan komputasi kami konsisten dengan hasil dalam artikel .

Menjalankan algoritma dalam produksi

Setelah algoritma dikembangkan, didebug dan diuji dalam percobaan komputasi, tibalah saatnya untuk menjalankannya. Algoritme diimplementasikan dalam C ++ dan ditempatkan dalam DLL yang terhubung ke aplikasi 1C sebagai komponen eksternal dari tipe asli. Baca tentang komponen eksternal 1C dan cara mengembangkan dan menghubungkannya dengan benar ke aplikasi 1C di sini . Dalam program "1C: Warehouse Management 3", formulir pemrosesan dikembangkan di mana pengguna dapat memulai prosedur untuk mengompresi residu dengan parameter yang ia butuhkan. Tangkapan layar formulir ditunjukkan di bawah ini.

Gbr. 13. Bentuk prosedur untuk "kompresi" saldo dalam Lampiran 1C: Manajemen Gudang 3

Pengguna dapat memilih parameter kompresi untuk residu dalam bentuk:

Mode kompresi: dengan pengelompokan batch (lihat artikel pertama) dan tanpa itu.
Gudang, di sel-sel yang diperlukan untuk melakukan kompresi. Dalam satu ruangan bisa ada beberapa gudang untuk organisasi yang berbeda. Situasi seperti itu terjadi pada klien kami.
Selain itu, pengguna dapat secara interaktif menyesuaikan jumlah barang yang ditransfer dari sel donor ke wadah dan menghapus item dari daftar untuk kompresi, jika karena alasan tertentu ia ingin agar tidak berpartisipasi dalam prosedur kompresi.

Kesimpulan

Pada akhir artikel ini saya ingin merangkum pengalaman yang didapat sebagai hasil dari pengenalan algoritma optimasi.

. : , , . - :
1. , ;
2. .
( ), , . «», - . , , . , , , - , .
, ( ), . , , . , . . , .
:
1. .
2. .
3. . , .
4. . , . , , , , .
5. , . ( ) . , .
6. .

Dan, saya pikir, hal yang paling penting. Proses optimisasi dalam perusahaan seringkali harus mengikuti setelah selesainya proses informatisasi. Optimasi tanpa informasi awal tidak banyak berguna , karena tidak ada tempat untuk mendapatkan data dan tidak ada tempat untuk menulis data dari solusi algoritma. Saya berpikir bahwa sebagian besar perusahaan domestik menengah dan besar telah menutup kebutuhan dasar untuk otomatisasi dan informatisasi dan siap untuk lebih mengoptimalkan proses "fine-tuning".

Oleh karena itu, kami berlatih setelah penerapan sistem informasi, baik itu ERP, WMS, TMS, dll. buat ekstra kecil. proyek untuk mengoptimalkan proses-proses yang diidentifikasi selama implementasi sistem informasi sebagai masalah dan penting bagi klien. Saya pikir ini adalah praktik yang menjanjikan yang akan mendapatkan momentum di tahun-tahun mendatang.

, ,
, .

Matematika diskrit untuk WMS: algoritma untuk mengompresi barang dalam sel (bagian 2)