Studi modal kontrol sistem levitasi magnetik

Materi ini dibuat mengingat pertahanan masa lalu dari pekerjaan kualifikasi akhir bujangan, dengan mempertimbangkan beberapa komentar pada objek kontrol. Bahan ini dibuat sebagai cadangan awal untuk tesis master yang mungkin pada subjek yang sama.

Sistem levitasi magnetik modern semakin banyak digunakan: kereta penumpang berkecepatan tinggi, isolasi mekanisme yang peka terhadap getaran, bantalan magnetik, levitasi logam cair di tungku induksi, serta levitasi billet logam. Baru-baru ini, efek levitasi magnetik juga digunakan pada perangkat rumah tangga.

Mungkin aplikasi yang paling signifikan ditemukan di kereta api dengan sistem levitasi pada superkonduktor. Dan ini karena keunggulan seperti keandalan yang lebih besar (karena kurangnya gesekan), konsumsi daya yang relatif rendah, dan kemampuan untuk mengembangkan kecepatan tinggi.

Namun, karena persamaan gerak objek nonlinear yang menggambarkan dinamikanya, sulit untuk mereproduksi proses mengendalikan objek. Ini akan tentang posisi (jarak) objek relatif terhadap tanda nol.

Singkatnya, levitasi magnetik adalah posisi yang stabil dari suatu objek pada jarak tertentu dalam medan gravitasi, ketika, pada umumnya, percepatan gravitasi dikompensasi oleh percepatan objek, yang diciptakan oleh medan magnet. Dalam hal ini, gaya angkat muncul.

Levitasi magnetik diwujudkan menggunakan diamagnetik, sistem arus eddy dan superkonduktor, serta menggunakan servomekanisme.

Dalam artikel saat ini (di bawah potongan), kami akan mempertimbangkan kontrol modal untuk sistem levitasi magnetik linierisasi, serta penerapan kontrol modal untuk model sistem nonlinear.

Model matematika

Pertimbangkan skema levitasi magnetik sederhana.

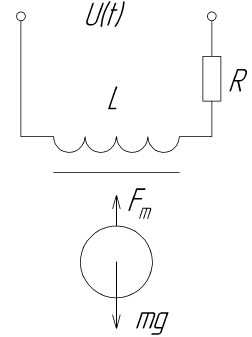
Diagram ini menunjukkan elektromagnet yang berinteraksi dengan medan magnet dari objek kontrol, yang merupakan magnet permanen-bola. Melalui perubahan gaya tarik elektromagnet, efek levitasi akan tercapai.

Dalam karya terakhir, objek orde kedua dipertimbangkan, di mana satu komponen penting, arus dalam koil, tidak termasuk dalam vektor keadaan. Kali ini komponen ini akan diperkenalkan.

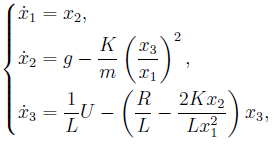
dimana $$$x_1$- posisi objek;

$$$x_2$- tingkat perubahan posisi objek;

$$$g$- percepatan gravitasi;

$$$K$Apakah konstan;

$$$m$- massa benda bola;

$$$x_3$- arus dalam koil;

$$$L$- induktansi koil;

$$$U$- tegangan input;

$$$R$- resistensi aktif koil.

Nilai beberapa variabel di atas dirangkum dalam sebuah tabel.

Untuk mendapatkan model linier, seseorang harus membuat sistem persamaan.

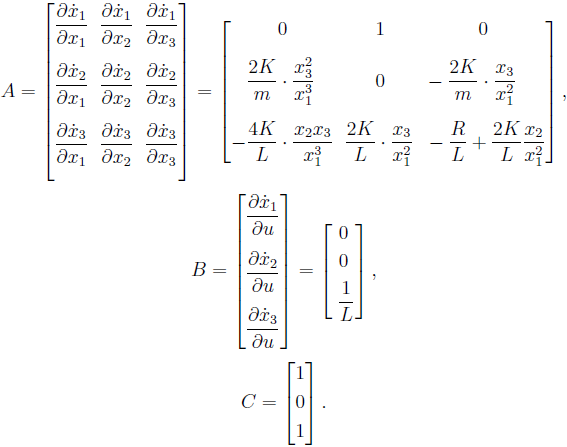
Tampilan matriks $$$C$dapat dibenarkan oleh fakta bahwa variabel vektor menyatakan seperti posisi ( $$$x_1$) dan saat ini ( $$$x_3$)

Dalam bentuk ini, matriks yang dihasilkan masih tidak cocok untuk pemodelan. Untuk melakukan ini, kami menetapkan kondisi awal.

$$

$$x_1 ^ {\ left \ {0 \ right \}} = 0.005, ~ x_2 ^ {\ left \ {0 \ right \}} = 0.$$

$$

$$g - \ frac {K (x_3 ^ {\ left \ {0 \ right \}}) ^ 2} {m (x_1 ^ {\ left \ {0 \ right \}}}) ^ 2} = 0$$

$$

$$x_3 ^ {\ left \ {0 \ right \}} = \ sqrt {\ frac {gm} {K}} x_1 ^ {\ left \ {0 \ right \}} = 0,063 ~ \ text {A}.$$

Pengganti sekarang data yang diperoleh dan $$$x_3 ^ {\ left \ {0 \ right \}}$ untuk menemukan nilai sinyal input pada saat awal:

$$

$$U ^ {\ left \ {0 \ right \}} = \ left (R - \ frac {2Kx_2 ^ {\ left \ {0 \ right \}}}} {(x_1 ^ {\ left \ {0 \ right \ }}) ^ 2} \ kanan) x_3 ^ {\ kiri \ {0 \ kanan \}} = Rx_3 ^ {\ kiri \ {0 \ kanan \}} = 1,95 ~ \ teks {B}.$$

Pemodelan

Sekarang Anda dapat mensintesis kontrol. Untuk penelitian, paket Matlab dipilih. Di bawah ini adalah kode untuk mendapatkan koefisien regulator oleh negara:

g = 9.81; K = 0.659*10^-3; m = 0.0106; L = 0.109; R = 31.1; x10 = 0.005; x20 = 0; x30 = sqrt(g*m/K)*x10; u = R*x30; A = [0 1 0; 2*K*x30^2/(m*x10^3) 0 -2*K*x30/(m*x10^2); -4*K*x20*x30/(L*x10^3) 2*K*x30/(L*x10^2) -R/L+2*K*x20/(L*x10^2)]; B = [0; 0; 1/L]; C = [1 0 0]; W = ctrb(A, B); %   detW = det(W); poles = [-10 -10 -10]; %  K = acker(A, B, poles); %  system = ss(A - B*K, B, C, 0); %   figure(1) step(system) %   km = 1/dcgain(system); %   system_m = ss(A - B*K, B*km, C, 0); figure(2) step(system_m) 

Untuk memahami apakah mungkin untuk mensintesis kontrol untuk sistem yang dihasilkan, Anda harus mengetahui matriks pengontrolan, dengan penentu kesimpulan yang dibuat:

 >> detW detW = -7.5351e+07 

Determinannya bukan nol, oleh karena itu, sistem yang dilinearisasi dapat dikontrol.

Kutub vektor adalah vektor yang berisi kutub yang diinginkan dari sistem levitasi magnetik yang dilinearisasi.

Saat menerapkan efek pengujian dalam bentuk langkah tunggal, kami mendapatkan hasil berikut:

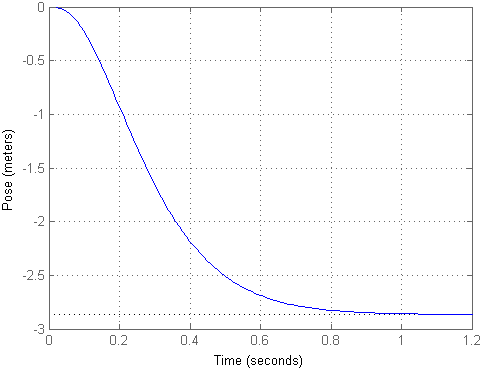
Seperti yang Anda lihat, ternyata benda itu terbang jarak yang cukup besar dengan sedikit benturan, meskipun benda itu tetap berada di posisi yang sama. Agar input sesuai dengan output, kita dapat menghitung km faktor penskalaan dan melipatgandakan sinyal input dengan itu, yang diwujudkan dalam model kedua. Maka proses transisi akan terlihat seperti ini:

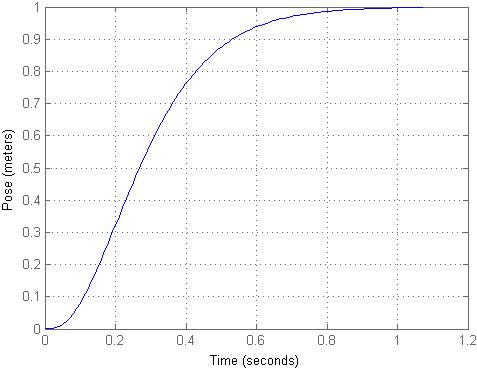
Posisi yang dihasilkan masih bagus untuk instalasi seperti itu. Untuk saat ini, mari kita abaikan arus dan langsung ke model Simulink, di mana kita mempertimbangkan hal-hal yang tersisa.

Kami skala sinyal input sehingga nilai-nilai output direpresentasikan dalam sentimeter. Kami menerapkan beberapa tindakan uji pada input untuk memeriksa bagaimana transien dalam sistem terlihat, serta arus yang mengalir.

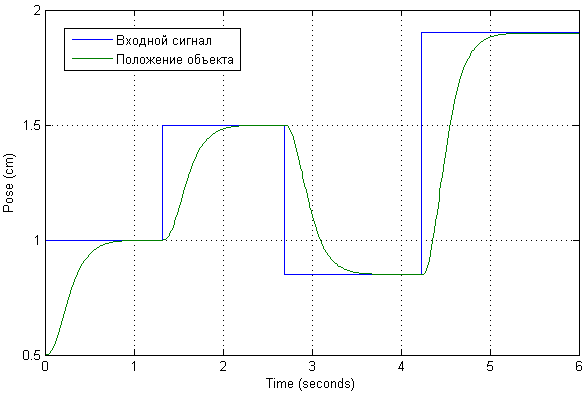
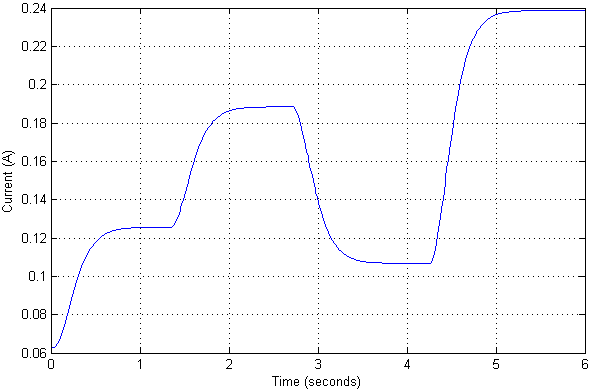
Ternyata nilai saat ini pada posisi objek tidak begitu signifikan. Transien itu sendiri dalam posisi bersifat aperiodik, tanpa overshoot dan kesalahan statis. Sebenarnya, itu diatur oleh kutub yang diinginkan dari sistem yang disesuaikan.

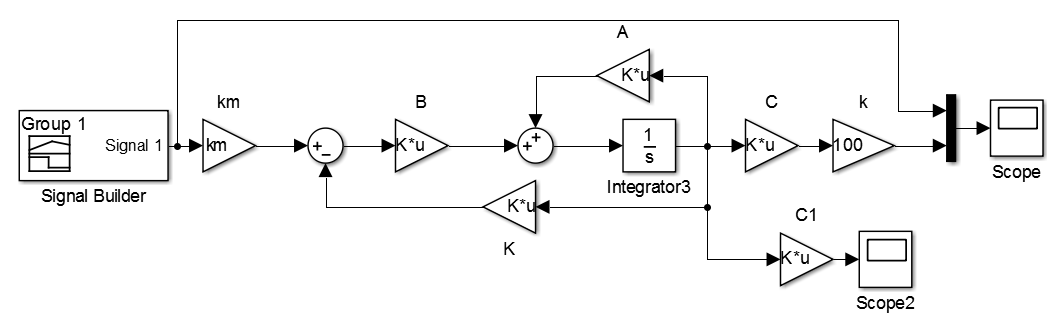
Namun, perkiraan ini pada titik operasi mungkin tidak berfungsi dengan benar dengan model nonlinear asli. Lihat ini. Model sistem non-linear dengan pengontrol yang terhubung ditunjukkan di bawah ini.

Ini adalah versi final yang tersisa setelah semua percobaan. Keterbatasan ditetapkan pada tegangan input (0-12V) dan posisi objek itu sendiri (0-4cm). Komponen kedua dari regulator dikeluarkan, karena dengan itu proses transisi tidak stabil:

Setelah perubahan pada rangkaian, transien sekarang terlihat seperti ini:

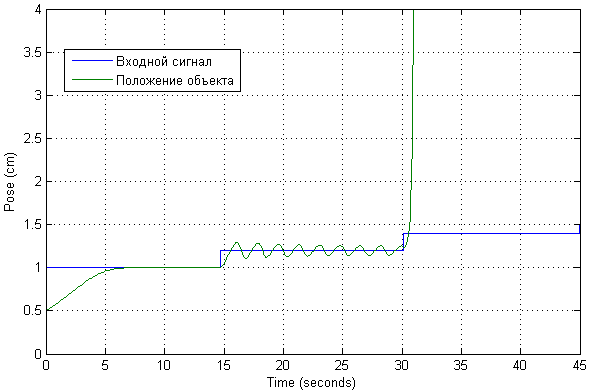
Kemungkinan jangkauan operasi sistem seperti itu segera diperiksa. Anda dapat melihat bahwa posisi yang diinginkan akan dicapai dengan sedikit penyimpangan dari titik awal. Dalam hal ini, manifestasi osilasi yang signifikan dimungkinkan.

Dalam hal ini, nilai saat ini adalah sebagai berikut:

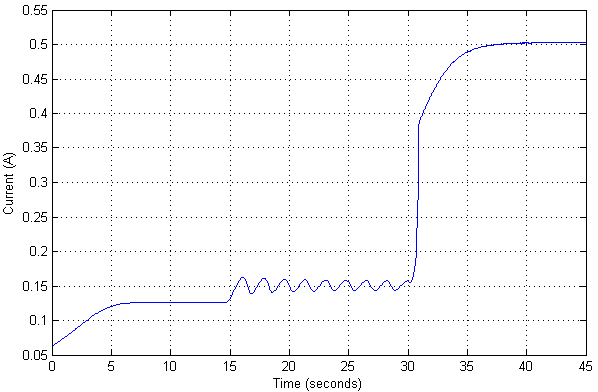
Karena sudah ada pemeriksaan untuk model non-linear dari suatu objek, Anda juga dapat melihat berapa nilai posisi maksimum untuk suatu objek di mana ia masih tidak kehilangan stabilitas.

Setelah pemodelan dengan sinyal input yang berbeda, diketahui bahwa model linierisasi sangat baik. Jadi di sini kita akan menunjukkan transien sesuai dengan sinyal input awal meningkat 10 kali lipat.

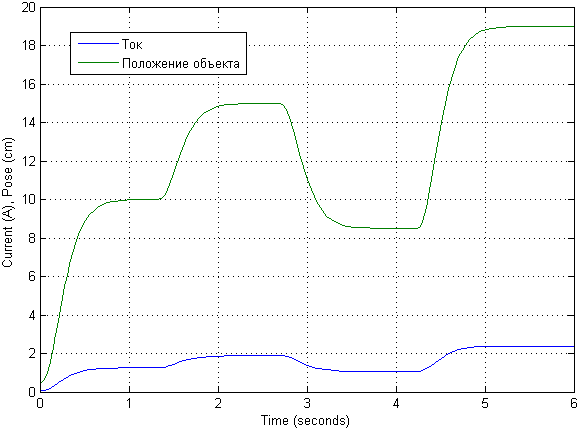
Model matematika itu sendiri mungkin terlihat sedikit berbeda. Deskripsi diambil dari deskripsi model matematika.

Kesimpulan

Kontrol modal untuk model sistem levitasi magnetik yang tidak linier ini sama sekali tidak cocok untuk kebutuhan praktis apa pun. Implementasi lain untuk sistem levitasi magnetik ini harus dipertimbangkan.

Adapun pekerjaan sarjana, penulis menerapkan instalasi sederhana pada levitasi, yang akan dijelaskan secara terpisah di masa depan.