Hilbert, Lebesgue ... and the Void

Di bawah potongan, pertanyaan tentang bagaimana algoritma pengindeksan multidimensi yang baik harus diselidiki diselidiki. Anehnya, tidak ada begitu banyak pilihan.

Indeks Satu Dimensi, Pohon-B

Ukuran keberhasilan algoritma pencarian akan dianggap 2 fakta -

1. penetapan fakta ada atau tidak adanya hasil terjadi untuk jumlah logaritmik (sehubungan dengan ukuran indeks) pembacaan halaman disk
2. biaya mengeluarkan hasil sebanding dengan volumenya

Dalam hal ini, pohon-B cukup berhasil dan alasannya dapat dianggap sebagai penggunaan pohon seimbang. Kesederhanaan algoritme ini disebabkan oleh satu dimensi ruang utama - jika perlu, bagi halaman, cukup untuk membagi dua elemen elemen halaman ini. Secara umum dibagi dengan jumlah elemen, meskipun ini tidak perlu.

Karena halaman-halaman pohon disimpan pada disk, dapat dikatakan bahwa B-tree memiliki kemampuan untuk secara efisien mengkonversi ruang kunci satu dimensi ke ruang disk satu dimensi.

Saat mengisi pohon dengan “penyisipan kanan” yang kurang lebih, dan ini merupakan kasus yang cukup umum, halaman dihasilkan dalam urutan pertumbuhan kunci, dari waktu ke waktu bergantian dengan halaman yang lebih tinggi. Ada kemungkinan besar bahwa mereka akan berada di disk juga. Dengan demikian, tanpa upaya apa pun, lokalitas data tinggi tercapai - data yang dekat nilainya akan berada di suatu tempat di dekatnya dan di disk.

Tentu saja, ketika memasukkan nilai-nilai dalam urutan acak, kunci dan halaman dihasilkan secara acak, sebagai akibat dari apa yang disebut indeks fragmentasi. Ada juga alat anti-fragmentasi yang mengembalikan lokalitas data.

Tampaknya di zaman kita disk RAID dan SSD urutan membaca dari disk tidak masalah. Tetapi, lebih tepatnya, itu tidak memiliki arti yang sama seperti sebelumnya. Tidak ada penerusan fisik kepala di SSD, sehingga kecepatan baca acaknya tidak turun ratusan kali dibandingkan dengan pembacaan solid, seperti HDD. Dan hanya sekali setiap 10 atau lebih .

Ingatlah bahwa B-tree muncul pada tahun 1970 di era pita magnetik dan drum. Ketika perbedaan dalam kecepatan akses acak untuk tape dan drum yang disebutkan itu jauh lebih dramatis daripada dibandingkan dengan HDD dan SSD.

Selain itu, 10 kali juga masalah. Dan 10 kali ini tidak hanya mencakup fitur fisik SSD, tetapi juga titik mendasar - prediktabilitas perilaku pembaca. Jika pembaca sangat mungkin meminta blok berikutnya untuk blok ini, masuk akal untuk mengunduhnya secara proaktif, dengan asumsi. Dan jika perilakunya kacau, semua upaya prediksi tidak ada artinya dan bahkan berbahaya.

Pengindeksan multidimensi

Selanjutnya kita akan berurusan dengan indeks titik dua dimensi (X, Y), hanya karena nyaman dan intuitif untuk bekerja dengan mereka. Tetapi masalahnya pada dasarnya sama.

Opsi sederhana, "tidak canggih" dengan indeks terpisah untuk X dan Y tidak lulus sesuai dengan kriteria kesuksesan kami. Itu tidak memberikan biaya logaritmik untuk mendapatkan poin pertama. Bahkan, untuk menjawab pertanyaan, adakah yang ada dalam batas yang diinginkan, kita harus

• lakukan pencarian di indeks X dan dapatkan semua pengidentifikasi dari X-interval
• mirip untuk Y
• memotong dua set pengidentifikasi ini

Sudah item pertama tergantung pada ukuran sejauh dan tidak menjamin logaritma.

Untuk menjadi "sukses," indeks multidimensi harus disusun sebagai pohon yang kurang lebih seimbang. Pernyataan ini mungkin tampak kontroversial. Tetapi persyaratan pencarian logaritma menentukan bagi kita hanya perangkat semacam itu. Mengapa tidak dua pohon atau lebih? Sudah dianggap sebagai opsi "tidak canggih" dan tidak cocok dengan dua pohon. Mungkin ada yang cocok. Tapi dua pohon - ini dua kali lebih banyak (termasuk simultan) kunci, dua kali lebih banyak biaya, peluang yang jauh lebih besar untuk menangkap jalan buntu. Jika Anda dapat bertahan dengan satu pohon, Anda harus menggunakannya.

Mengingat semua ini, keinginan untuk mengambil sebagai dasar pengalaman B-tree yang sangat sukses dan "menggeneralisasi" untuk bekerja dengan data dua dimensi cukup wajar.

Jadi pohon-R muncul.

R-tree

R-tree diatur sebagai berikut:
Awalnya, kami memiliki halaman kosong, cukup tambahkan data (poin) ke dalamnya.
Tapi di sini halamannya penuh dan harus dibagi.
Di B-tree, elemen halaman diurutkan secara alami, jadi pertanyaannya adalah berapa banyak yang harus dipotong. Tidak ada tatanan alami di R-tree. Ada dua opsi:

• Bawa pesanan, mis. memperkenalkan fungsi yang, berdasarkan X&Y, akan memberikan nilai sesuai dengan elemen halaman mana yang akan dipesan dan dibagi sesuai dengan itu. Dalam hal ini, seluruh indeks berdegenerasi menjadi B-tree reguler yang dibangun dari nilai-nilai fungsi yang ditentukan. Selain plus yang jelas, ada pertanyaan besar - baik, baik, kami diindeks, tapi bagaimana cara melihatnya? Lebih lanjut tentang itu nanti, pertimbangkan opsi kedua.
• Bagilah halaman dengan kriteria spasial. Untuk melakukan ini, setiap halaman harus ditetapkan sejauh elemen yang terletak di / di bawahnya. Yaitu halaman root memiliki luas seluruh lapisan. Saat memisahkan, dua (atau lebih) halaman dihasilkan yang luasannya termasuk dalam luas halaman induk (untuk pencarian).

Ada banyak ketidakpastian. Bagaimana tepatnya membagi halaman? Horisontal atau vertikal? Lanjutkan dari setengah area atau setengah dari elemen? Tetapi bagaimana jika titik membentuk dua kelompok, tetapi Anda hanya dapat memisahkannya dengan garis diagonal? Dan jika ada tiga kelompok?

---

Kehadiran pertanyaan semacam itu menunjukkan bahwa R-tree bukan sebuah algoritma. Ini adalah seperangkat heuristik, setidaknya untuk memisahkan halaman selama penyisipan, untuk menggabungkan halaman selama penghapusan / modifikasi, untuk preprocessing untuk penyisipan massal.

Heuristik melibatkan spesialisasi pohon tertentu pada tipe data tertentu. Yaitu pada dataset dari jenis tertentu, dia kurang melakukan kesalahan. “Heuristik tidak bisa sepenuhnya keliru, karena dalam hal ini, itu akan menjadi sebuah algoritma ”©.

Apa artinya kesalahan heuristik dalam konteks ini? Sebagai contoh, bahwa halaman akan terpecah / digabung tidak berhasil dan halaman akan mulai tumpang tindih sebagian. Jika tiba-tiba tingkat pencarian jatuh pada area tumpang tindih halaman, biaya pencarian sudah tidak cukup logaritmik. Seiring waktu, saat Anda memasukkan / menghapus, jumlah kesalahan menumpuk dan kinerja pohon mulai menurun.


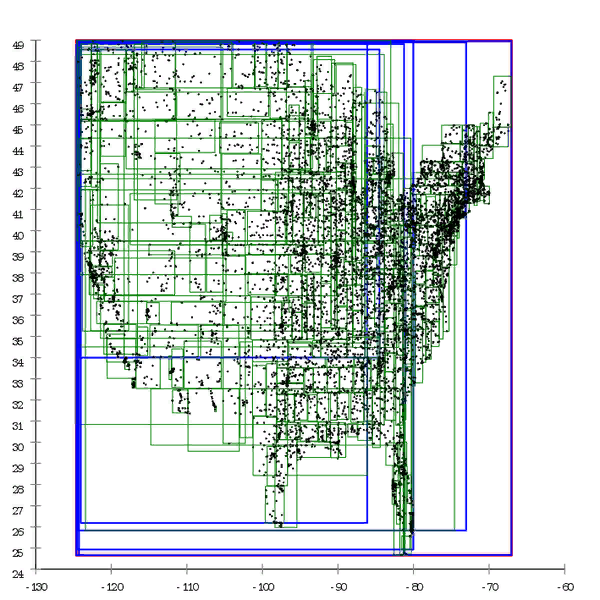Gambar 1 Berikut adalah contoh pohon R *, yang dibangun secara alami.


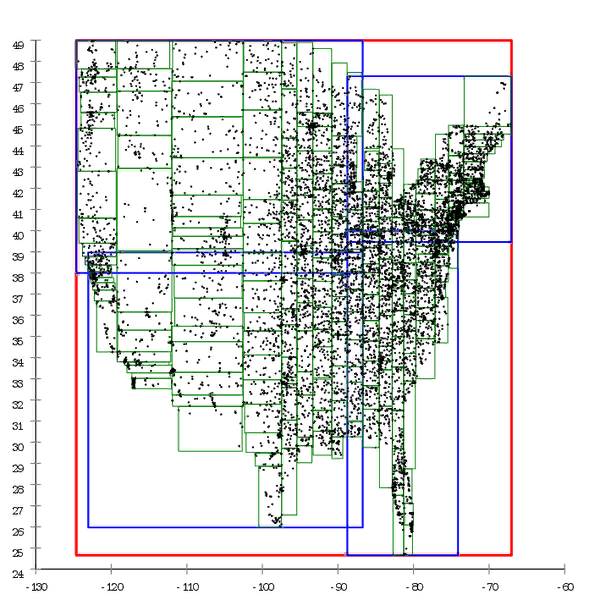Gambar 2 Dan di sini dataset yang sama adalah pra-diproses dan pohon dibangun dengan penyisipan massal

Kita dapat mengatakan bahwa B-tree juga mengalami degradasi seiring waktu, tetapi ini adalah degradasi yang sedikit berbeda. Kinerja B-tree turun karena fakta bahwa halamannya tidak berturut-turut. Ini mudah diobati dengan "meluruskan" pohon - defragmentasi. Dalam kasus R-tree, tidak mudah untuk menghilangkannya, struktur pohon itu sendiri adalah "kurva" untuk memperbaiki situasi;

Generalisasi dari R-tree ke ruang multidimensi tidak jelas. Misalnya, saat memisahkan halaman, kami meminimalkan batas halaman anak. Apa yang harus dikurangi dalam kasus tiga dimensi? Volume atau luas permukaan? Dan dalam kasus delapan dimensi? Akal sehat tidak lagi menjadi penasihat.

Ruang yang diindeks mungkin non-isotropik. Mengapa tidak mengindeks bukan hanya poin, tetapi posisi mereka tepat waktu, mis. (X, Y, t). Dalam hal ini, misalnya, heuristik berdasarkan perimeter tidak ada artinya sejak itu menumpuk panjang pada interval waktu.

Kesan umum dari R-tree adalah sesuatu seperti krustasea insang . Mereka memiliki ceruk ekologis sendiri di mana sulit untuk bersaing dengan mereka. Tetapi dalam kasus umum, mereka tidak memiliki peluang untuk bersaing dengan hewan yang lebih maju.

Pohon quad

Dalam quadtree, setiap halaman non-daun memiliki empat keturunan, yang membagi ruang menjadi kuadran.


Gambar 3 Contoh pohon quad dibangun

Ini bukan desain basis data yang baik.

• Setiap halaman mempersempit ruang pencarian untuk setiap koordinat hanya dua kali. Ya, ini memberikan kompleksitas logaritma pencarian, tetapi ini adalah logaritma basis 2, bukan jumlah elemen pada halaman, (bahkan 100) seperti dalam B-tree.
• Setiap halaman kecil, tetapi di belakangnya Anda masih harus pergi ke disk.
• Kedalaman pohon quad harus dibatasi, jika tidak, ketidakseimbangannya mempengaruhi kinerja. Akibatnya, pada data yang sangat berkerumun (misalnya, rumah di peta - ada banyak kota di kota, sedikit di bidang) sejumlah besar data dapat terakumulasi di halaman daun. Indeks dari indeks yang tepat menjadi kuning dan membutuhkan pasca pemrosesan.
  
  Ukuran kisi yang dipilih dengan buruk (kedalaman pohon) dapat membunuh kinerja. Namun demikian, saya ingin agar kinerja algoritma tidak bergantung secara kritis pada faktor manusia.
  
• Biaya ruang untuk menyimpan satu titik cukup besar.

Penomoran ruang

Masih mempertimbangkan versi yang sebelumnya ditangguhkan dengan fungsi yang, berdasarkan kunci multidimensi, menghitung nilai untuk menulis dalam B-tree reguler.

Konstruksi indeks semacam itu jelas, dan indeks itu sendiri memiliki semua keunggulan B-tree. Satu-satunya pertanyaan adalah apakah indeks ini dapat digunakan untuk pencarian yang efektif.

Ada sejumlah besar fungsi seperti itu, dapat diasumsikan bahwa di antara mereka ada sejumlah kecil "baik", sejumlah besar "buruk" dan sejumlah besar "hanya mengerikan".

Menemukan fungsi yang mengerikan tidak sulit - kami membuat serial kunci menjadi string, pertimbangkan MD5 darinya dan dapatkan nilai yang sama sekali tidak berguna untuk keperluan kami.

Dan bagaimana cara mendekati yang baik? Sudah dikatakan bahwa indeks yang berguna menyediakan "lokalitas" data - titik yang dekat dalam ruang dan sering dekat satu sama lain ketika disimpan ke disk. Seperti yang diterapkan pada fungsi yang diinginkan, ini berarti bahwa untuk titik dekat spasi ia memberikan nilai dekat.

Setelah di indeks, nilai yang dihitung akan muncul pada halaman "fisik" dalam urutan nilainya. Dari sudut pandang "pengertian fisik", tingkat pencarian harus memengaruhi halaman indeks fisik sesedikit mungkin. Apa yang umumnya jelas. Dari sudut pandang ini, kurva penomoran yang "menarik" data adalah "buruk". Dan orang-orang yang "bingung dalam bola" - lebih dekat dengan "baik".

Penomoran naif

Upaya untuk memeras segmen ke dalam kotak (hypercube) sambil tetap dalam logika ruang satu dimensi yaitu potong-potong dan isi kotak dengan potongan-potongan ini. Itu bisa saja


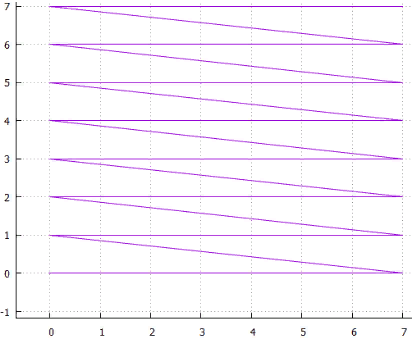Pemindaian 4 baris


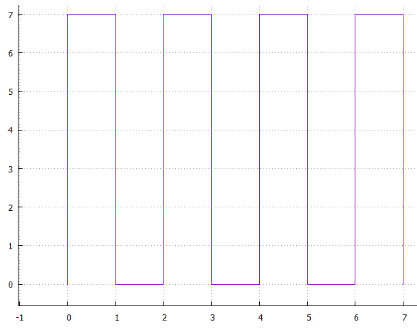5 interlaced


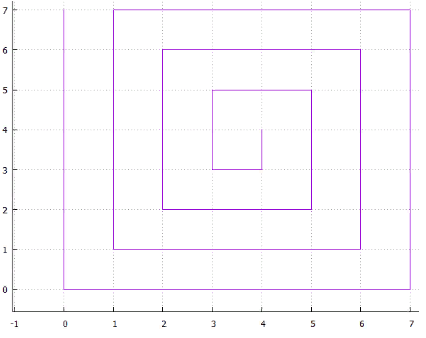Gbr.6 spiral

atau ... Anda dapat memunculkan banyak opsi, semuanya memiliki dua kelemahan

1. ambiguitas, misalnya: mengapa spiral melengkung searah jarum jam dan tidak menentangnya, atau mengapa pemindaian horizontal pertama sepanjang X dan kemudian sepanjang Y
   
2. keberadaan potongan lurus panjang yang membuat penggunaan metode seperti itu tidak efektif untuk pengindeksan multidimensi (perimeter halaman besar)

Fitur akses langsung

Jika klaim utama untuk metode "naif" adalah bahwa mereka menghasilkan halaman yang sangat panjang, mari kita buat halaman "benar" sendiri.

Idenya sederhana - biarkan ada pembagian ruang eksternal ke dalam blok, tetapkan pengidentifikasi untuk setiap blok dan ini akan menjadi kunci indeks spasial.

• biarkan koordinat X&Y menjadi 16-bit (untuk kejelasan)
• kita akan menutup ruang dengan blok persegi ukuran 1024X1024
• kasar koordinat, bergeser 10 bit ke kanan
• dan dapatkan ID halaman, rekatkan bit dari X&Y. Sekarang di pengidentifikasi 6 digit bawah adalah yang tertua dari X, 6 digit berikutnya adalah yang tertua dari Y
  

Sangat mudah untuk melihat bahwa blok-blok membentuk pemindaian garis, oleh karena itu, untuk menemukan data untuk tingkat pencarian, Anda harus melakukan pencarian / baca dalam indeks untuk setiap baris blok yang menjadi batas ini. Secara umum, metode ini bekerja dengan baik, meskipun memiliki beberapa kelemahan.

• saat membuat indeks, Anda harus memilih ukuran blok optimal, yang sama sekali tidak terlihat
• jika blok secara signifikan lebih besar dari kueri tipikal, pencarian akan menjadi tidak efisien sejak itu harus membaca dan memfilter (postprocessing) terlalu banyak
  
• jika blok secara signifikan lebih kecil dari kueri tipikal, pencarian akan menjadi tidak efisien sejak itu harus melakukan banyak pertanyaan baris demi baris
  
• jika blok memiliki terlalu banyak atau terlalu sedikit data rata-rata, pencarian akan menjadi tidak efektif
  
• jika data dikelompokkan (mis: di rumah di peta), pencarian tidak akan efektif di mana-mana
• jika dataset telah tumbuh, mungkin ternyata ukuran blok tidak lagi optimal.
  

Sebagian, masalah ini diselesaikan dengan membangun blok multi-level. Untuk contoh yang sama:

• masih ingin blok 1024X1024
• tapi sekarang kita masih akan memiliki blok tingkat atas ukuran 8X8 blok yang lebih rendah
• kuncinya diatur sebagai berikut (dari rendah ke tinggi):
  3 digit - digit 10 ... 12 koordinat X
  3 digit - digit 10 ... koordinat 12 Y
  3 digit - digit 13 ... 15 X koordinat
  3 digit - digit 13 ... 15 Y koordinat

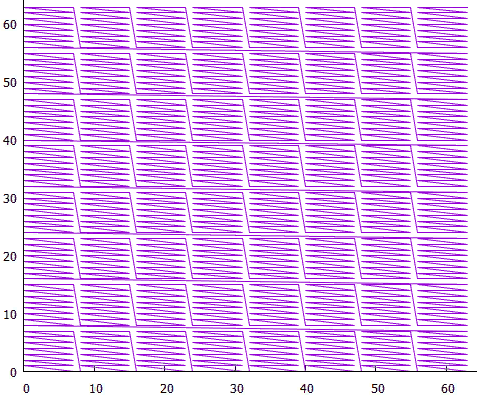7 Blok tingkat rendah membentuk blok tingkat tinggi

Sekarang untuk luasan besar Anda tidak perlu membaca sejumlah besar blok kecil, ini dilakukan dengan mengorbankan blok tingkat tinggi.

Menariknya, adalah mungkin untuk tidak memperkeras koordinat, tetapi dengan cara yang sama untuk menekan mereka ke dalam kunci. Dalam hal ini, post-filtering akan lebih murah karena akan terjadi saat membaca indeks.

Indeks GRID spasial diatur dalam MS SQL dengan cara yang sama, hingga 4 level blok diizinkan di dalamnya.


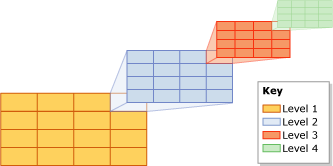Gbr.8 Indeks GRID

Cara lain yang menarik dari pengindeksan langsung adalah dengan menggunakan pohon quad untuk partisi ruang eksternal.

Pohon quad berguna karena dapat beradaptasi dengan kepadatan objek sejak itu ketika node meluap, ia terbelah. Akibatnya, di mana kepadatan objek tinggi, blok akan menjadi kecil dan sebaliknya. Ini mengurangi jumlah panggilan indeks kosong.

Benar, pohon quad adalah konstruksi yang tidak nyaman untuk membangun kembali dengan cepat, menguntungkan untuk melakukan ini dari waktu ke waktu.

Dari hal yang menyenangkan, ketika membangun kembali pohon quad, tidak perlu membangun kembali indeks jika blok diidentifikasi oleh kode Morton dan objek dikodekan menggunakannya. Begini caranya: jika koordinat titik dikodekan dengan kode Morton, pengenal halaman adalah awalan dalam kode itu. Saat mencari data halaman, semua kunci yang berada dalam kisaran dari [awalan] 00 ... 00B hingga [awalan] 11 ... 11B dipilih, jika halaman dipecah, itu berarti hanya awalan dari keturunannya yang telah diperpanjang.

Fitur mirip diri

Hal pertama yang terlintas dalam pikiran ketika menyebutkan fungsi yang mirip dengan diri sendiri adalah "kurva sapuan". "Kurva yang terlihat adalah pemetaan berkelanjutan, domain yang merupakan segmen unit [0, 1], dan domain adalah ruang Euclidean (lebih ketat, topologis)." Contohnya adalah kurva Peano.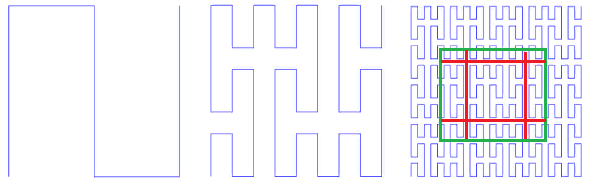


Gambar. 9 iterasi pertama dari kurva Peano

Di sudut kiri bawah adalah awal dari area definisi (dan nilai nol fungsi), di sudut kanan atas ujung (dan 1), setiap kali kita memindahkan 1 langkah, tambahkan 1 / (N * N) ke nilai (asalkan N - derajat 3, tentu saja). Hasilnya, di sudut kanan atas nilainya mencapai 1. Jika kita menambahkan satu di setiap langkah, fungsi seperti itu hanya memberi nomor kisi kuadrat secara berurutan, yang merupakan apa yang kita inginkan.

Semua kurva sweeping hampir sama. Dalam hal ini, simpleks adalah bujur sangkar 3x3. Pada setiap iterasi, setiap titik simpleks berubah menjadi simpleks yang sama, untuk memastikan kontinuitas, Anda harus menggunakan pemetaan (membalik).

Kesamaan diri adalah kualitas yang sangat penting bagi kami. Ini memberi harapan untuk nilai logaritma pencarian. Misalnya, untuk simpleks 3x3, semua angka yang dihasilkan dalam masing-masing dari 9 kotak dasar dengan iterasi detail berikutnya akan berada dalam kisaran yang sama. Hanya karena jumlahnya adalah jalur yang dilalui sejak awal. Yaitu jika Anda membagi luasnya menjadi 9 bagian, konten masing-masing dapat diperoleh dengan satu indeks lintasan. Dan seterusnya secara rekursif, masing-masing dari 9 sub-kotak dari masing-masing kotak dapat diperoleh dengan satu permintaan pada indeks (meskipun dalam kisaran yang lebih kecil). Jadi jangkauan pencarian dapat dipecah menjadi sejumlah kecil kuadrat persegi, dibaca secara keseluruhan atau dengan pemfilteran (sekitar batas). Gambar 9 menunjukkan tingkat pencarian dalam warna hijau, dipecah oleh garis merah menjadi subquery.

Namun, kemiripan diri tidak secara otomatis membuat kurva penomoran cocok untuk keperluan pengindeksan.

• kurva harus mengisi kisi kuadrat. Kami mengindeks nilai dalam node kisi kuadrat dan setiap kali kami tidak ingin mencari node yang sesuai pada kisi, misalnya, segitiga. Setidaknya untuk menghindari masalah pembulatan. Di sini, misalnya, seperti (Gambar 10)
  
  
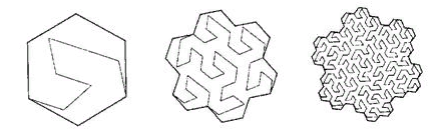
  Gambar 10 danau ternary Kokha
  
  kurva tidak cocok untuk kita. Meskipun, itu sempurna "menjembatani" permukaan.
  
• kurva harus mengisi ruang tanpa celah ( dimensi fraktal D = 2). Ini dia (Gbr. 11):
  
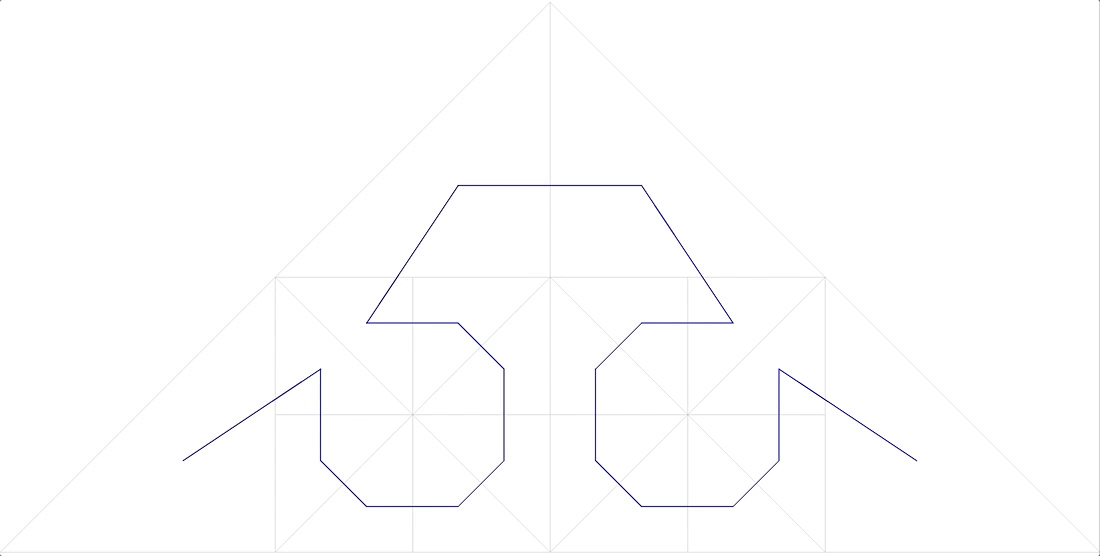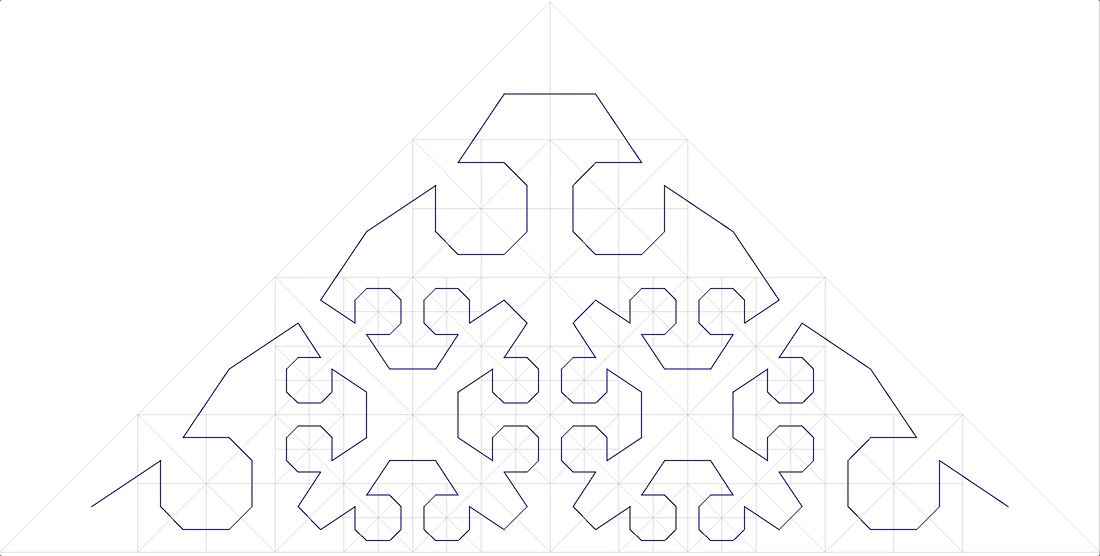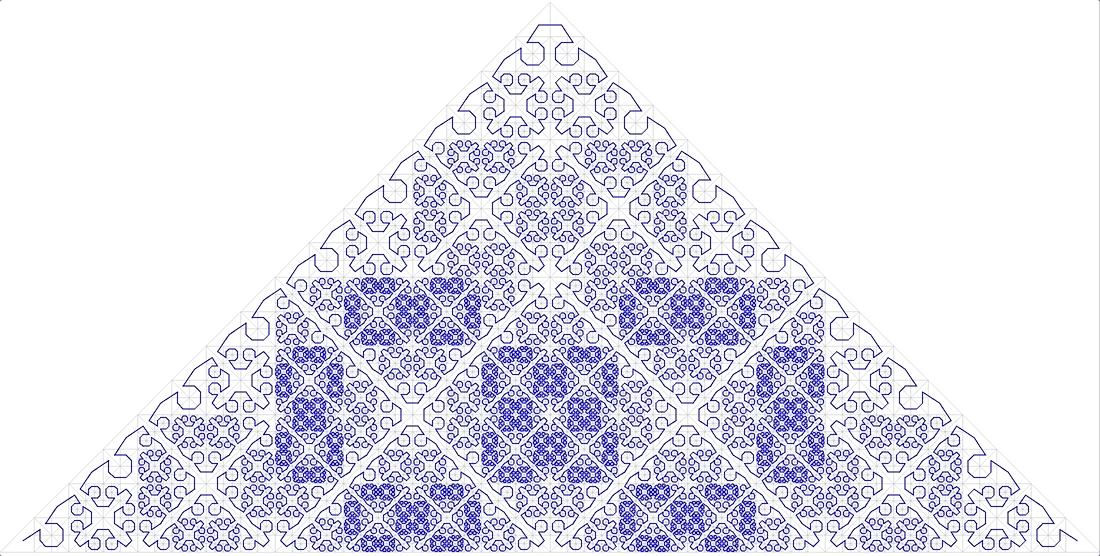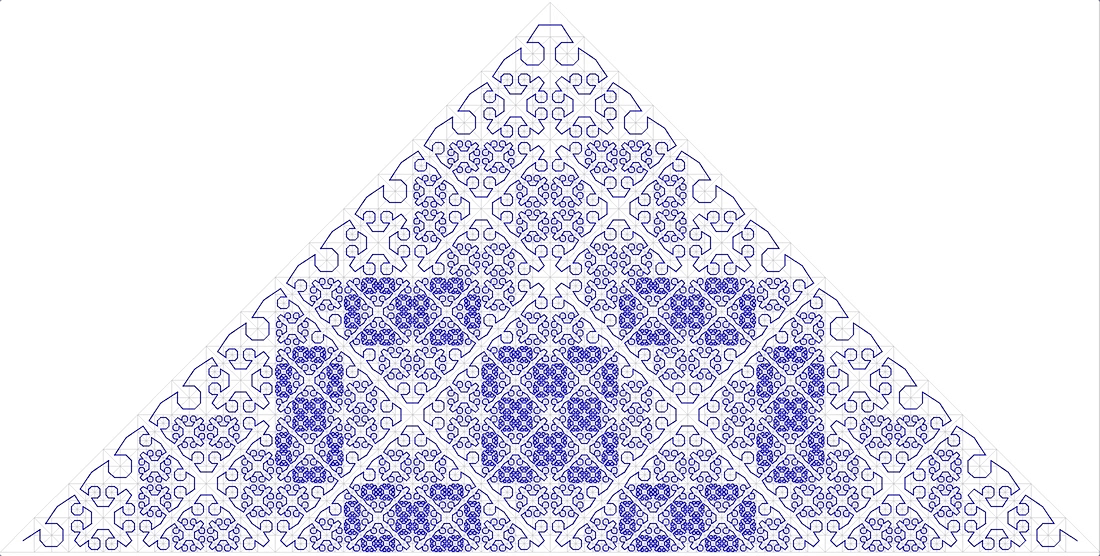
  11 kurva fraktal anonim
  
  juga tidak cocok.
  
• (, ) . , ,
  
  
  .12
  
  , ( ), “ ”
  
  
  . 13 , 85°
• , ( ). . : ( )
  
  
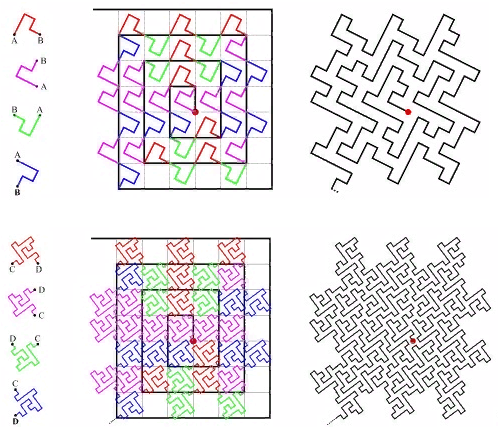
  . 14 “A Plane Filling Curve for the Year 2017”
  
  , ( ) .
  , , , .

Isotropi adalah karakteristik penting lainnya. Dapat dipahami bahwa fungsi penomoran harus mudah digeneralisasikan ke dimensi yang lebih tinggi. Dan ada baiknya jika untuk kubus N-dimensi semua proyeksi N-nya pada dimensi (N-1) adalah sama. Ini mengikuti dari fakta bahwa kami menggunakan ruang isotropik dan akan aneh jika sumbu yang berbeda digunakan dalam fungsi yang berbeda.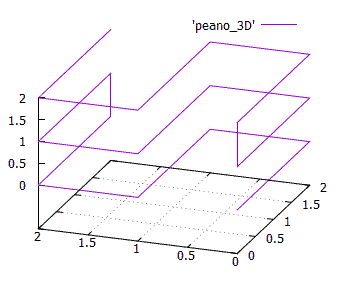


Gbr. 15 Simpleks tiga dimensi dari kurva Peano 3x3x3

Isotropi bukan persyaratan yang ketat, tetapi merupakan indikator penting dari kualitas kurva penomoran.

Mengenai kontinuitas .

Di atas, kami melihat contoh fungsi penomoran berkelanjutan yang tidak sesuai untuk tujuan kami. Di sisi lain, fungsi pemindaian garis yang cukup terputus dengan blok sangat bagus untuk ini (dengan beberapa batasan). Tidak hanya itu, jika kami membuat indeks blok berdasarkan pemindaian interlaced berkelanjutan, ini tidak akan mengubah apa pun dalam hal kinerja. Karena jika blok dibaca secara keseluruhan, tidak ada perbedaan dalam urutan apa objek akan diterima.

Untuk kurva mirip diri ini juga benar.

• mari kita sebut ukuran halaman, luasnya semua objek pada halaman disk
  
• ukuran karakteristik akan menjadi area halaman rata-rata
• ( ) , . , . — . .
• — , .. .
  
• , . , , . , , — () 3...10% () Z-.
  
  — , .

Dari apa yang telah dikatakan, dapat disimpulkan bahwa untuk keperluan pengindeksan multidimensi, hanya simpleks kuadrat (hiperkubik) yang diterapkan secara berulang sebanyak yang diperlukan (untuk detail kisi yang cukup).

Ya, ada cara serupa lainnya untuk menjembatani kisi persegi, namun, tidak ada cara yang murah secara komputasi untuk melakukan transformasi semacam itu, termasuk sebaliknya. Mungkin trik numerik seperti itu ada, tetapi mereka tidak diketahui oleh penulis. Selain itu, simpleks kuadrat memungkinkan untuk secara efektif membagi tingkat pencarian menjadi subquery dengan memotong sepanjang salah satu koordinat . Dengan batas yang terputus antara simpleks, ini tidak mungkin .

Mengapa simpleks persegi dan bukan persegi panjang? Untuk alasan isotropi.

Tetap memilih ukuran dan penomoran yang sesuai di dalam simpleks (bypass).

Untuk memilih ukuran simpleks , Anda perlu mencari tahu apa pengaruhnya. Jumlah subqueries yang dihasilkan yang harus dibuat selama pencarian. Misalnya, simpleks 3X3 dari kurva Peano dipotong menjadi 3 subquery dengan interval angka kontinu, pertama dalam X, dan kemudian masing-masing dari mereka menjadi 3 bagian dalam Y. Akibatnya, kita kembali ke tahap rekursi berikutnya. Jika kita memiliki simpleks 5X5 (interlaced) yang serupa, itu harus dipotong menjadi 5 bagian. Atau menjadi bagian yang tidak sama (mis: 2 + 3), yang aneh.

Ini mengingatkan salah satu pohon pencarian dalam beberapa cara - Anda tentu saja dapat menggunakan pohon 5-desimal dan 7-desimal, tetapi dalam praktiknya hanya pohon biner yang digunakan. Pohon Tritunggalmemiliki ceruk sempit sendiri untuk pencarian dengan awalan. Dan ini bukan apa yang secara intuitif dipahami sebagai pohon ternary.

Ini dijelaskan oleh efisiensi. Dalam simpul ternary, untuk memilih keturunan, seseorang harus membuat 2 perbandingan. Di pohon biner, ini sesuai dengan pilihan di antara 4 opsi. Bahkan kedalaman pohon yang lebih pendek tidak menghalangi hilangnya produktivitas dari peningkatan jumlah perbandingan.

Selain itu, jika 3X3 lebih efektif daripada 2X2 hanya karena 3> 2, 4X4 akan lebih efektif daripada 3X3, dan 8X8 lebih efektif daripada 5X5. Anda selalu dapat menemukan kekuatan yang tepat dari dua, yang dibentuk oleh beberapa iterasi 2X2 ...

Dan apa yang dipengaruhi oleh simplex bypass ? Pertama-tama, jumlah subquery yang dihasilkan oleh pencarian. Karenaitu baik jika simpleks memungkinkan Anda untuk memotong-motong diri Anda dengan interval angka terus menerus. Di sini Peano 3X3 memungkinkan, jadi satu iterasi memotongnya menjadi 3 bagian. Dan jika Anda mengambil simpleks 8x8 dengan ksatria catur (Gbr. 16), satu-satunya pilihan adalah segera memiliki 64 elemen.


Gbr. 16 Salah satu opsi untuk menghindari simpleks 8x8

Jadi, karena kami menemukan bahwa simpleks optimal adalah 2x2, kita harus mempertimbangkan opsi apa yang ada untuknya.


Gbr. 17 Pilihan untuk menghindari simpleks 2x2

Ada tiga, hingga simetri, yang disebut “Z”, “omega” dan “alpha”.
Segera menangkap mata bahwa "alpha" melintasi dirinya sendiri, dan karena itu tidak cocok untuk pemisahan biner. Itu harus segera dipotong menjadi 4 bagian. Atau 256 dalam kasus 8 dimensi.

Kemampuan untuk menggunakan algoritme tunggal untuk ruang dimensi yang berbeda (yang kita kehilangan dalam kasus kurva seperti "alpha") terlihat sangat menarik. Karenanya, di masa depan kami hanya akan mempertimbangkan dua opsi pertama.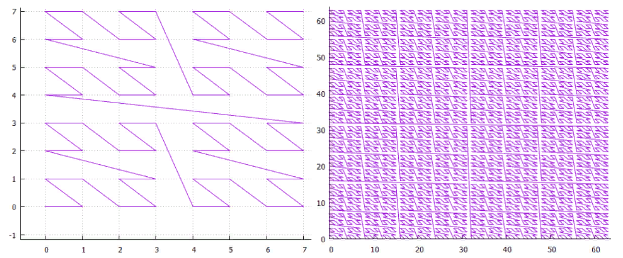


Gbr. 18 Z-kurva dari


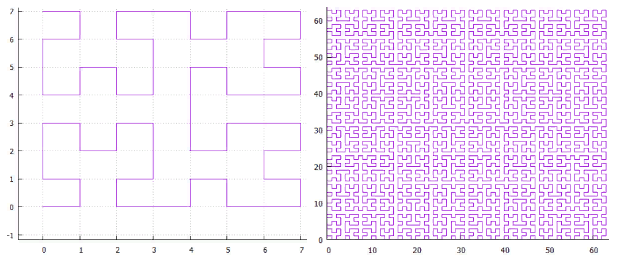Gbr. 19 "omega" - kurva Hilbert.

Setelah kurva ini memiliki hubungan dekat, mereka dapat diproses dengan satu algoritma. Spesifisitas utama kurva terlokalisasi dalam pemisahan subquery.

• pertama kita menemukan tingkat awal, ini adalah persegi panjang minimum yang mencakup tingkat pencarian dan berisi satu interval berkesinambungan dari nilai-nilai kunci.
  Ditemukan sebagai berikut -
  
  • menghitung nilai kunci untuk titik kiri bawah dan kanan atas dari tingkat pencarian (KMin, KMax)
    
  • ( ) KMin, KMax
    
  • , SMin, , SMax
    
  • . , , SMin, . .
  • , , ( ).
    
  • Z- . z- — , — ( ). , , .
• • , , . ,
  • , . — “ ” >= “ ” () , “ ”
    
    
    • “ ” > , ,
      
    • , ,
      
    • “ ” > , , ,
    • pisahkan huruf "kunci terakhir" == nilai maksimum dari subquery saat ini, diproses secara terpisah dengan melintasi maju
      
  • pisahkan subquery saat ini
    • tambahkan 0 dan 1 ke awalannya - kami mendapatkan dua awalan baru
    • isi sisa kunci 0 atau 1 - kami mendapatkan nilai minimum dan maksimum dari subqueries baru
    • Kami mendorong mereka ke tumpukan, pertama yang ditambah 1, lalu 0. Ini untuk pembacaan indeks searah.
  
  

Pada kurva Z, kerjanya seperti ini:


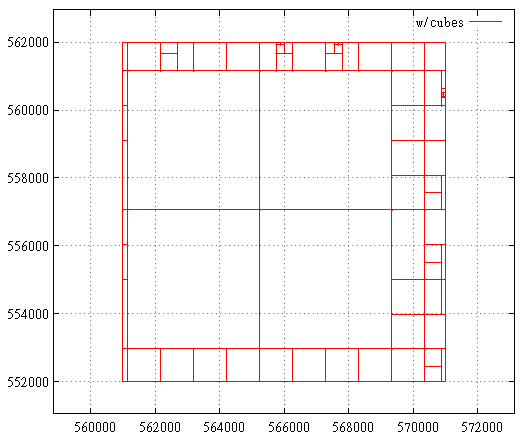Gbr. 20 - pemisahan sub-permintaan jika Z-curve


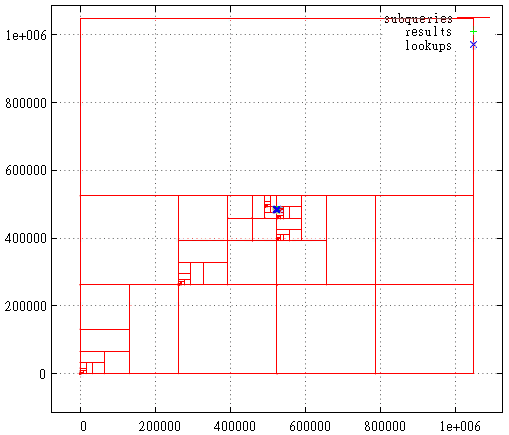Gbr. 21 Hilbert curve, kasus ketika tingkat awal adalah maksimum

Tahap pertama ditunjukkan di sini - memotong lapisan berlebih dari batas maksimum.


Gbr. 22 Hilbert Curve, area permintaan pencarian

Dan di sini adalah perincian ke dalam sub-kueri, poin yang ditemukan, dan mengindeks panggilan di area permintaan pencarian. Ini masih permintaan yang sangat gagal dari sudut pandang kurva Hilbert. Biasanya semuanya kurang berdarah.

Namun, statistik kueri mengatakan bahwa (secara kasar) pada data yang sama, indeks dua dimensi berdasarkan kurva Hilbert membaca rata-rata halaman disk 5% lebih sedikit, tetapi berfungsi setengah lebih lambat. Perlambatan juga disebabkan oleh kenyataan bahwa perhitungan itu sendiri (langsung dan mundur) dari kurva ini jauh lebih sulit - 2000 jam prosesor untuk Hilbert dibandingkan dengan 50 untuk kurva-Z.

Dengan berhenti mendukung kurva Hilbert, algoritme dapat disederhanakan, sekilas, perlambatan seperti itu tidak dapat dibenarkan. Di sisi lain, ini hanya kasus dua dimensi, misalnya, dalam ruang 8 dimensi atau lebih, statistik dapat bersinar dengan warna yang sama sekali baru. Masalah ini masih menunggu klarifikasi.

PS : Kurva Z kadang-kadang disebut kurva bit-interleaving karena algoritma untuk menghitung nilai - digit dari masing-masing koordinat jatuh ke dalam nilai kunci melalui satu, yang sangat teknologi. Tapi Anda bisa, setelah semua, interleave buangan tidak secara individual, tetapi dalam paket 2,3 ... 8 ... potongan. Sekarang, jika kita mengambil 8 bit, maka pada kunci 32-bit kita mendapatkan analog dari indeks GRID 4-tingkat dari MS SQL. Dan dalam kasus yang ekstrim - masing-masing satu pak 32 bit - suatu algoritma pemindaian horizontal.

Indeks seperti itu (bukan huruf kecil, tentu saja) bisa sangat efektif, bahkan lebih efisien daripada kurva-Z pada beberapa set data. Sayangnya, karena kehilangan keumuman.

PPS : Indeks yang dijelaskan sangat mirip dengan bekerja dengan pohon quad. Batas maksimum adalah halaman root dari pohon quad, ia memiliki 4 keturunan ... Dan karena itu, algoritme dapat dikaitkan dengan "metode akses langsung".

Perbedaan masih mendasar.

Pohon quad tidak disimpan di mana pun, itu virtual, tertanam dalam sifat nomor. Tidak ada batasan pada kedalaman pohon, kami memperoleh informasi tentang populasi keturunan dari populasi pohon utama. Selain itu, pohon utama dibaca sekali, kita beralih dari nilai terkecil ke nilai tertua. Ini lucu, tetapi struktur fisik B-tree memungkinkan untuk menghindari pertanyaan kosong dan membatasi kedalaman rekursi.

Satu hal lagi - pada setiap iterasi hanya dua keturunan yang muncul - dari mereka 4 subquery dapat dihasilkan, dan tidak dapat dihasilkan jika tidak ada data di bawahnya. Dalam kasus 3 dimensi, kita akan berbicara tentang 8 keturunan, dalam kasus 8 dimensi - sekitar 256.

PPPS : di awal artikel ini, kita berbicara tentang dikotomi ketika mencari dalam indeks multidimensi - untuk mendapatkan nilai logaritmik, perlu untuk membagi beberapa sumber daya yang terbatas pada setiap iterasi - baik ruang nilai kunci atau ruang pencarian. Dalam algoritma yang disajikan, dikotomi ini runtuh - kami secara bersamaan berbagi kunci dan ruang.

"Saya tinggal di kedua pekarangan, dan pohon-pohon saya selalu lebih tinggi."

PPPPS : Begitu mereka memanggil kurva-Z, di sini Anda memiliki urutan-Z dan interleaving-bit dan kode / kurva Morton. Itu juga dikenal sebagai kurva Lebesgue, sehingga untuk menjaga keseimbangan, penulis berhak artikel, termasuk untuk menghormati Henry Leon Lebesgue .

PPPPPS : Dalam ilustrasi judul, pemandangan Gletser Fedchenko cukup indah, dan ada kekosongan yang cukup. Bahkan, penulis terkesan dengan bagaimana berbagai ide dan metode mengalir dengan lancar satu sama lain, secara bertahap bergabung menjadi satu algoritma. Sama seperti banyak sumber air kecil yang membentuk daerah tangkapan air membentuk limpasan tunggal.