Permukaan acak menyembunyikan urutan rumit

Matematikawan telah membuktikan bahwa proses acak ketika diterapkan pada permukaan acak selalu menghasilkan pola-pola tertentu

Dalam artikel aslinya, ini adalah gambar tiga dimensi yang dapat diputar

Dalam film tentang pencarian Tabut yang hilang, Indiana Jones harus mencari ruang rahasia untuk menyembunyikan Tabut Perjanjian yang legendaris. Untuk menentukan lokasinya yang tepat, Indiana perlu menemukan peta khusus, yang hanya terlihat ketika matahari bersinar melalui kristal khusus di ruangan tertentu pada waktu tertentu dalam sehari.

Gagasan serupa - bahwa informasi paling penting hanya dapat diungkapkan dengan kebetulan yang tepat dari keadaan tertentu - ditemukan dalam banyak mitos. Ini terjadi dalam matematika, kadang-kadang dalam situasi yang tidak terduga. Sekarang, tiga matematikawan telah membuktikan bahwa jika jenis keacakan tertentu sangat tepat disetel, maka bentuk geometris yang rumit muncul - seperti peta dengan harta karun di lantai biasa.

Potongan-potongan ini seperti sel-sel catur yang tersebar di atas kisi-kisi, yang pada gilirannya dibuat sendiri oleh proses acak. Orang akan berpikir bahwa menumpuk keacakan ke dalam keacakan, kita mendapatkan kebingungan. Ternyata, seperti dalam kasus kepingan salju, ketika masing-masing dari mereka adalah unik, tetapi pada saat yang sama semuanya adalah kepingan salju, kekacauan itu menyatu menjadi bentuk universal - jika saja kondisinya ternyata tepat seperti yang dibutuhkan.

Titik balik

Semua orang tahu bahwa bentuk studi matematika. Sebagian besar formulir ini mengikuti aturan deterministik: jika saya memberi Anda petunjuk untuk membuat bola, Anda akan menerima bola yang sama setiap saat.

Tetapi bahkan ahli matematika mempelajari bentuk-bentuk yang diperoleh sebagai hasil dari proses acak, seperti, misalnya, jalan acak - jalan, arah setiap langkah yang dipilih secara acak. Selain jalan acak, ada jenis objek geometri acak lainnya, misalnya, permukaan dua dimensi acak (bayangkan lanskap tempat bukit dan lembah tersebar secara acak) dan peta acak (satu set titik acak yang dihubungkan oleh garis).


Permukaan acak diperoleh dengan menempelkan segitiga

Semua bentuk tersebut berbeda satu sama lain. Namun, matematikawan telah menemukan bahwa proses acak ini bertemu dengan bentuk kanonik tertentu. Sebagai contoh, semua jalan acak adalah bentuk gerak Brown dengan jalan yang agak panjang. Dalam beberapa tahun terakhir, matematikawan telah menemukan bentuk kanonik dan proses acak lainnya - dan menerima penghargaan tertinggi untuk ini di bidangnya.

Bukti baru terkait dengan pemahaman tentang sifat-sifat yang mendasari proses acak lain.

Dimulai dengan membuat permukaan acak. Pertama, Anda harus merekatkan segitiga menjadi satu. Maka mereka perlu dicocokkan bersama dengan cara apa pun, hanya agar formulir yang dihasilkan tertutup, seperti paket pada hadiah (tidak memiliki lubang). Jika Anda mulai dengan sejumlah segitiga di tangan Anda, Anda akan memiliki banyak peluang. Beberapa "triangulasi" ini akan menghasilkan permukaan yang hampir mulus yang terlihat seperti bola. Kebanyakan dari mereka akan terlihat lebih kasar - seperti permukaan ekstrem yang menyerupai pegunungan.

"Itu tidak akan terlihat seperti bola biasa, itu akan memiliki paku besar seperti itu," kata Olivier Bernardi , seorang ahli matematika dari Universitas Brandeis, rekan penulis karya tersebut, yang juga melibatkan Nicholas Curien dari Universitas Paris-South XI dan Gregory Mjermont dari Higher Normal School di Lyon.


Olivier Bernardi, Nicholas Curien dan Gregory Myermont

Myermont dan ahli matematika lain, Jean-Francois le Gall , membangun banyak properti dari triangulasi acak ini dalam karya mereka sebelumnya. Bukti baru bahkan lebih jauh dengan menambahkan lapisan kedua keacakan di atas triangulasi acak.

Untuk menambahkan keacakan baru, tandai setiap titik di mana segitiga bertemu di sudut - yang oleh matematikawan disebut titik. Warnai simpul secara acak dalam hitam atau putih. Anda dapat melakukan ini dengan melempar koin, meskipun koin mungkin tidak sepenuhnya jujur, dan lebih besar di satu sisi.

Setelah melukis puncak, Anda dapat mengajukan berbagai pertanyaan tentang pola yang Anda buat. Salah satu yang mendasar: seberapa jauh Anda bisa menyusuri permukaan hanya menggunakan satu titik hitam? Proses bergerak di sepanjang simpul yang terhubung dengan warna yang sama disebut rembesan. Ini adalah cara matematika untuk mempelajari fenomena fisik dengan nama yang sama dengan fluida melewati media berpori.

Akan mudah untuk menyusup (atau tidak), tergantung pada bagaimana berat koin didistribusikan: jika koin cenderung memberikan simpul hitam, infiltrasi hampir dijamin; jika untuk ekstradisi kulit putih, rembesan hampir pasti tidak mungkin.



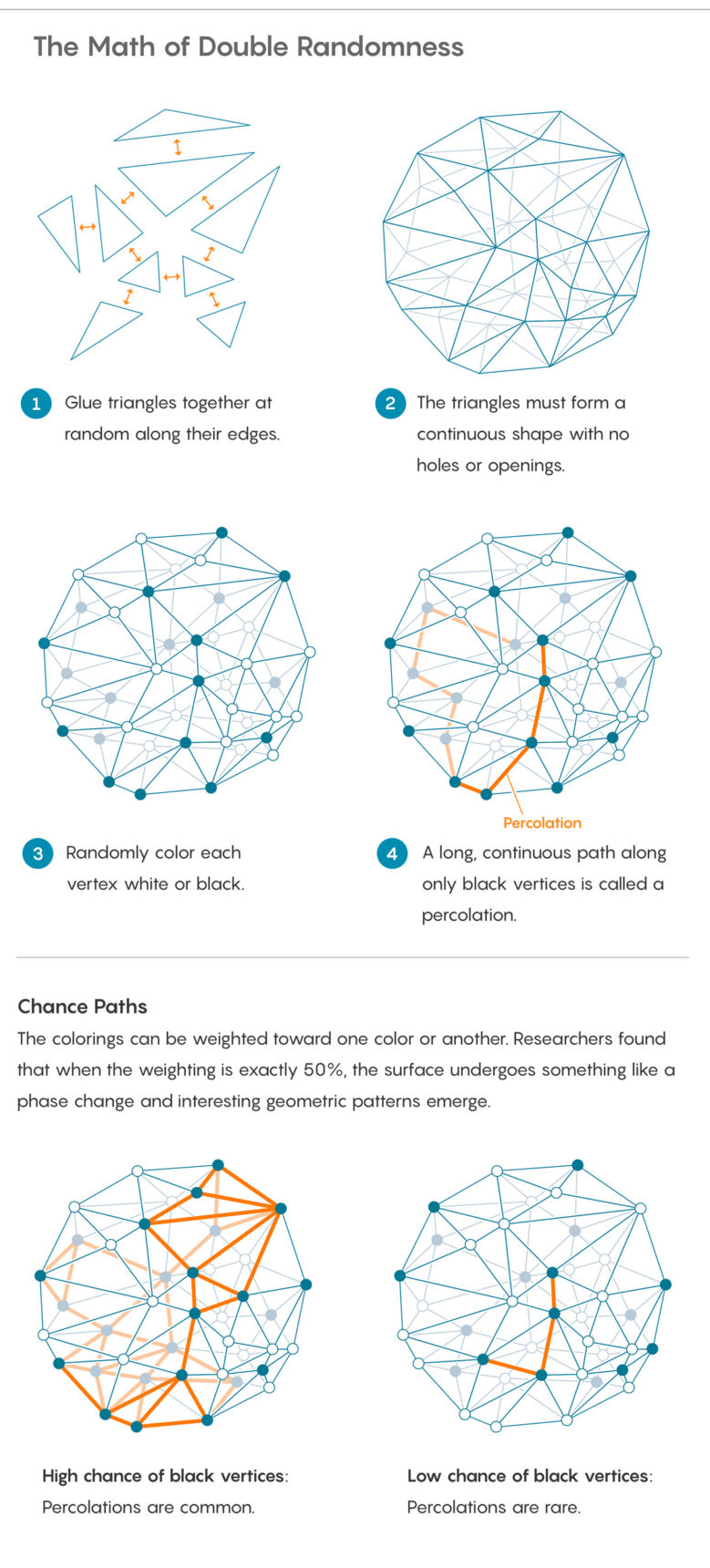
Bernardi, Curien dan Myermont mempelajari kasus-kasus yang jatuh di antara ekstrem ini - titik balik dalam perubahan berat koin, ketika kebocoran berubah dari fenomena yang hampir mustahil menjadi hampir dijamin. Mereka menyebut titik ini "ambang kritis". Ini adalah contoh transisi fase, momen ajaib ketika air panas tiba-tiba menjadi uap.

"Ambang kritis berarti bahwa jika saya sedikit menggeser parameter saya, maka perilaku sistem saya akan berubah dari dramatis ke dramatis dengan tanda berbeda," kata Curien.

Fisikawan tertarik pada transisi fase karena banyak fenomena alam paling penting terjadi di ambang. Matematikawan juga tertarik pada transisi fase, karena sifat matematika penting sering muncul hanya pada titik-titik ini.

"Kita tahu bahwa air mendidih pada 100 derajat, menciptakan semua pola gila ini, dan bentuk uap," kata Scott Sheffield , ahli matematika di MIT. “Terkadang perilaku gila dan liar menjadi sangat menarik. Transisi fase ini memanggil kita untuk memahaminya. ”

Dalam karya baru, tiga matematikawan membuktikan bahwa perilaku gila seperti itu memanifestasikan dirinya tepat dalam fase transisi kebocoran. Mereka menunjukkan bahwa pada ambang kritis ini bentuk geometris muncul - unik, dan pada saat yang sama bersifat universal.

Urutan tersembunyi secara kebetulan

Bagian pertama dari pekerjaan ini menentukan cara memperbaiki koin sehingga pewarnaan simpul jatuh pada ambang batas antara ada dan tidak adanya rembesan. Mengonfirmasi intuisi, mereka membuktikan bahwa koin ideal adalah nilai kritis - memberikan peluang 50% untuk jatuh hitam, dan 50% jatuh putih.

“Ini adalah bagian pertama dari pekerjaan. Kami membuktikan bahwa tepat setengahnya terjadi sesuatu yang menarik, ”kata Bernardi.


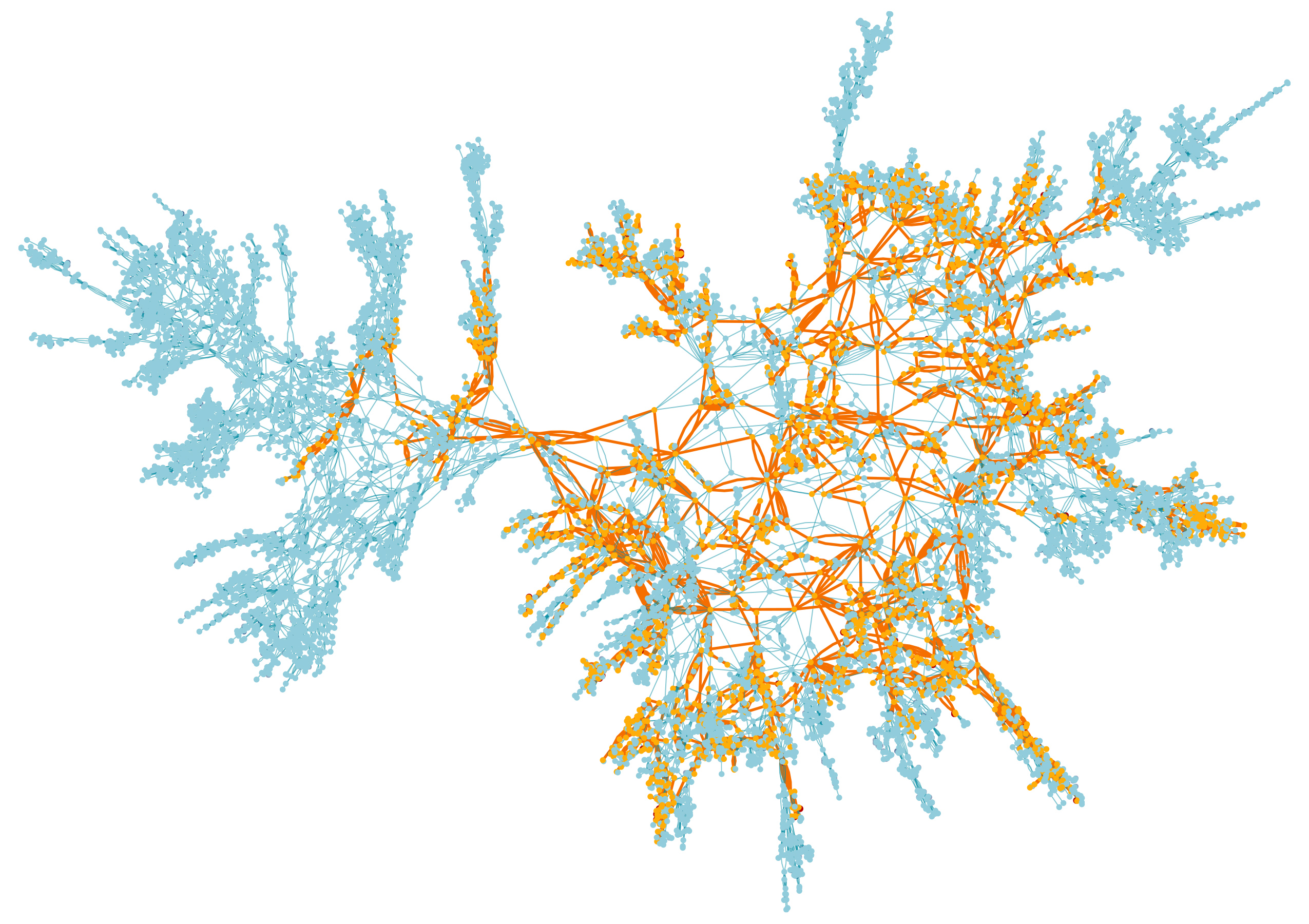Peta puncak dari permukaan acak, kelompok terbesar ditandai dengan oranye

Pada bagian kedua, kita mempelajari hal yang terjadi di sana. Mewarnai simpul dalam hitam dan putih dengan koin yang adil, Anda mendapatkan keseimbangan yang baik antara kelompok simpul hitam dan putih. Kluster tumbuh di sekitar satu sama lain, seperti semak gulma bersaing untuk mendapatkan tempat di kebun yang ditumbuhi, menciptakan bentuk-bentuk geometris kompleks yang tidak muncul ketika salah satu bunga mendominasi di antara puncak.

"Dengan memilih parameter kritis, Anda menemukan kelompok besar," kata Sheffield. "Namun, mereka tidak menodai semuanya, dan mereka tidak kecil."

Karena permukaan dibuat secara acak, dan proses pewarnaan simpul juga acak, kelompok besar di satu permukaan akan selalu berbeda dari kelompok besar di sisi lainnya. Tetapi matematikawan telah membuktikan bahwa untuk semua permukaan dan semua cara yang mungkin untuk mewarnai simpul mereka, kelompok terbesar akan memiliki sifat yang sama. Hal pertama yang mereka buktikan adalah distribusi probabilitas yang tepat dari ukuran cluster hitam terbesar di semua permukaan. Mereka menemukan bahwa paling sering sebuah cluster dengan ukuran menengah tertentu terjadi, dan bahwa frekuensi munculnya kelompok yang lebih besar atau lebih kecil meningkat secara eksponensial dengan jarak dari perantara ini.

Mereka juga berpendapat bahwa semua cluster besar dapat direduksi menjadi bentuk kanonik yang sama, yang dikenal sebagai "peta stabil". Peta stabil mengacu pada kelompok ini dengan cara yang sama seperti gerakan Brown untuk berjalan secara acak. Ini berarti bahwa jika masing-masing cluster sedikit terasing - sehingga setiap langkah acak di dalam cluster kurang terlihat dalam geometri seluruh gambar secara keseluruhan - maka cluster secara bertahap akan mencapai bentuk yang sama. Mereka tampak seperti butiran salju: mereka tampak unik di sekitarnya, tetapi kesamaan mereka jelas terlihat dari jauh.

"Mereka menemukan peta stabil ini, batas penskalaan alami," kata Sheffield.

Karya memperluas batas pengetahuan tentang bentuk acak dan proses yang diakumulasikan oleh ahli matematika dalam beberapa tahun terakhir. Ini juga mengungkapkan kepada kita bahwa justru pada saat itulah ketika sistem acak tampak paling kacau bahwa tatanan geometris yang luar biasa mulai terlihat melalui itu.