Ada dua pria bernama "Van Eck". Yang pertama, pada tahun 1985, menunjukkan kepada dunia cara mencegat data dari monitor (
Van Eck phreaking ) seharga $ 15, yang kedua, pada tahun 2010, muncul dengan urutan licik (urutan
Van Eck ). Lebih curam daripada kesederhanaan tugas urutan ini hanya dapat sifat dan misteri.
Jadi, algoritma untuk menghasilkan anggota urutan. Kami mengambil "nomor awal", misalnya, "0", tulis. Istilah berikutnya adalah berapa banyak langkah mundur nomor ini terjadi pada sub-urutan sebelumnya. Jika tidak pernah, maka tulis nol. Berikutnya adalah berapa banyak langkah mundur ada nol dalam sub-urutan sebelumnya, yaitu, satu langkah mundur. Kami menuliskan unit. Unit satu - tulis nol. Ups, nol bertemu dua langkah ke belakang. Kami menulis dua, dan seterusnya ...
Untuk titik laporan "0", 97 anggota pertama dari urutan:
0, 0, 1, 0, 2, 0, 2, 2, 1, 6, 0, 5, 0, 2, 6, 5, 4, 0, 5, 3, 0, 3, 2, 9, 0, 4, 9, 3, 6, 14, 0, 6, 3, 5, 15, 0, 5, 3, 5, 2, 17, 0, 6, 11, 0, 3, 8, 0, 3, 3, 1, 42, 0, 5, 15, 20, 0, 4, 32, 0, 3, 11, 18, 0, 4, 7, 0, 3, 7, 3, 2, 31, 0, 6, 31, 3, 6, 3, 2, 8, 33, 0, 9, 56, 0, 3, 8, 7, 19, 0, 5, 37, 0, 3, 8, 8, 1
Bagan:
Garis waktu yang lebih banyak:
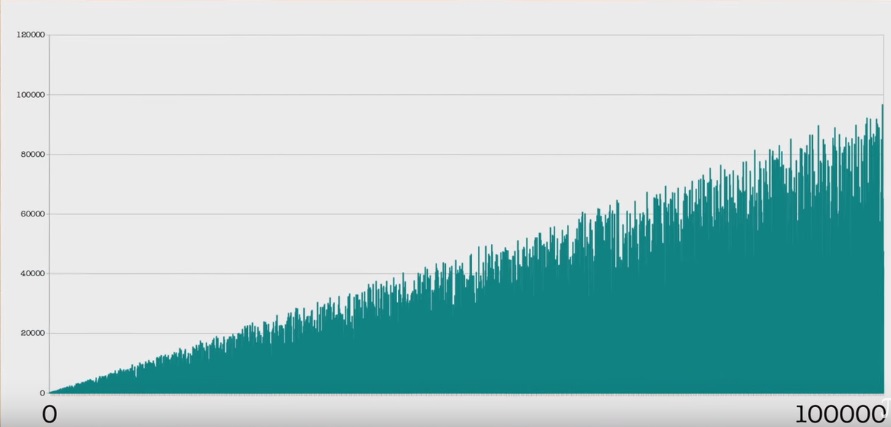
Sifat-sifat suatu urutan cukup mudah dibuktikan bahwa istilah maksimumnya meningkat setiap saat dan memiliki jumlah nol yang tak terbatas. Atau tidak ada periode di dalamnya. (Beberapa teorema dan konsekuensi di
sini .)
Grafik logaritmik:
Program dengan Python:
A181391 = [0] last_pos = {} for i in range(10**4): new_value = i - last_pos.get(A181391[i], i) A181391.append(new_value) last_pos[A181391[i]] = i
Untuk angka awal "1", seratus pertama adalah:
1, 0, 0, 1, 3, 0, 3, 2, 0, 3, 3, 1, 8, 0, 5, 0, 2, 9, 0, 3, 9, 3, 2, 6, 0, 6, 2, 4, 0, 4, 2, 4, 2, 2, 1, 23, 0, 8, 25, 0, 3, 19, 0, 3, 3, 1, 11, 0, 5, 34, 0, 3, 7, 0, 3, 3, 1, 11, 11, 1, 3, 5, 13, 0, 10, 0, 2, 33, 0, 3, 9, 50, 0, 4, 42, 0, 3, 7, 25, 40, 0, 5, 20, 0, 3, 8, 48, 0, 4, 15
Bagan:
Untuk angka awal "2", seratus pertama adalah:
2, 0, 0, 1, 0, 2, 5, 0, 3, 0, 2, 5, 5, 1, 10, 0, 6, 0, 2, 8, 0, 3, 13, 0, 3, 3, 1, 13, 5, 16, 0, 7, 0, 2, 15, 0, 3, 11, 0, 3, 3, 1, 15, 8, 24, 0, 7, 15, 5, 20, 0, 5, 3, 12, 0, 4, 0, 2, 24, 14, 0, 4, 6, 46, 0, 4, 4, 1, 26, 0, 5, 19, 0, 3, 21, 0, 3, 3, 1, 11, 42, 0, 6, 20, 34, 0, 4, 20, 4
Bagan:
Sumber