Layanan petunjuk baru untuk mencari hh.ru

Petunjuk pencarian sangat bagus. Seberapa sering kita mengetik alamat situs lengkap di bilah alamat? Dan nama produk di toko online? Untuk pertanyaan singkat seperti itu, mengetik beberapa karakter biasanya cukup jika petunjuk pencariannya bagus. Dan jika Anda tidak memiliki dua puluh jari atau kecepatan mengetik yang luar biasa, maka Anda pasti akan menggunakannya.
Pada artikel ini, kita akan berbicara tentang layanan petunjuk pencarian hh.ru baru kami, yang kami lakukan dalam edisi School of Programmer sebelumnya .

Layanan lama memiliki sejumlah masalah:

• ia mengerjakan kueri pengguna populer yang dipilih sendiri;
• tidak dapat beradaptasi dengan mengubah preferensi pengguna;
• tidak dapat membuat peringkat kueri yang tidak termasuk di bagian atas;
• tidak memperbaiki kesalahan ketik.

Dalam layanan baru, kami memperbaiki kekurangan ini (sambil menambahkan yang baru).

Kamus pertanyaan populer

Ketika tidak ada petunjuk sama sekali, Anda dapat secara manual memilih permintaan teratas-N pengguna dan menghasilkan petunjuk dari permintaan ini menggunakan kemunculan kata yang tepat (dengan atau tanpa urutan). Ini adalah pilihan yang bagus - mudah diimplementasikan, memberikan akurasi prompt yang baik dan tidak mengalami masalah kinerja. Untuk waktu yang lama, sugest kami bekerja seperti itu, tetapi kelemahan signifikan dari pendekatan ini adalah tidak lengkapnya masalah ini.

Misalnya, permintaan "pengembang javascript" tidak termasuk dalam daftar seperti itu, jadi ketika kita memasukkan "waktu javascript", kita tidak dapat menampilkan apa pun. Jika kami menambah permintaan, dengan hanya mempertimbangkan kata terakhir, kami akan melihat "tukang javascript" di tempat pertama. Untuk alasan yang sama, tidak mungkin untuk menerapkan koreksi kesalahan lebih sulit daripada pendekatan standar dengan menemukan kata-kata terdekat dengan jarak Damerau-Levenshtein.

Model bahasa

Pendekatan lain adalah belajar mengevaluasi probabilitas kueri dan menghasilkan kelanjutan yang paling mungkin untuk kueri pengguna. Untuk melakukan ini, gunakan model bahasa - distribusi probabilitas pada serangkaian urutan kata.



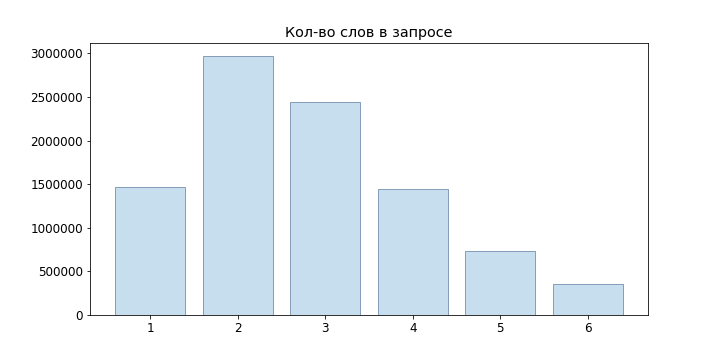
Karena sebagian besar permintaan pengguna pendek, kami bahkan tidak mencoba model bahasa jaringan saraf, tetapi membatasi diri pada n-gram:

$$

$$P (w_1 \ dots w_m) = \ prod_ {i = 1} ^ mP (w_i | w_1 \ dots w_ {i-1}) \ approx \ prod_ {i = 1} ^ mP (w_i | w_ {i- ( n-1)} \ dots w_ {i-1})$$

Sebagai model paling sederhana, kita dapat mengambil definisi statistik dari probabilitas

$$

$$P (w_i | w_1 \ dots w_ {i-1}) = \ frac {count (w_1 \ dots w_i)} {count (w_1 \ dots w_ {i-1})}$$

Namun, model seperti itu tidak cocok untuk mengevaluasi pertanyaan yang tidak ada dalam sampel kami: jika kami tidak mengamati 'junior developer java', maka ternyata

$$

$$P (\ text {junior developer java}) = \ frac {count (\ text {junior developer java})} {count (\ text {junior developer})} = 0$$

Untuk mengatasi masalah ini, Anda dapat menggunakan berbagai model perataan dan interpolasi. Kami menggunakan Backoff:

$$

$$P_ {bo} (w_n | w_1 \ dots w_ {n-1}) = \ begin {cases} {P} (w_n | w_1 \ dots w_ {n-1}), hitung (w_1 \ dots w_ {n- 1})> 0 \\ \ alpha {P_ {bo}} (w_n | w_2 \ titik w_ {n-1}), hitung (w_1 \ titik w_ {n-1}) = 0 \ end {kas}$$

$$

$$\ alpha = \ frac {P (w_1 \ dots w_ {n-1})} {1 - \ sum_wP_ {bo} (w | w_2 \ dots w_ {n-1})}$$

Di mana P adalah probabilitas yang dihaluskan $$$w_1 ... w_ {n-1}$ (kami menggunakan Laplace smoothing):

$$

$$P (w_n | w_1 \ dots w_ {n-1}) = \ frac {count (w_n) + \ delta} {count (w_1 \ dots w_ {n-1}) + \ delta | V |}$$

dimana V adalah kamus kami.

Pembuatan Opsi

Jadi, kami dapat menilai probabilitas permintaan tertentu, tetapi bagaimana cara menghasilkan permintaan yang sama? Adalah bijaksana untuk melakukan hal berikut: biarkan pengguna memasukkan kueri $$$w_1 ... w_n$ , maka pertanyaan yang cocok untuk kita dapat ditemukan dari kondisi tersebut

$$

$$w_1 \ dots w_m = \ underset {w_ {n + 1} \ dots w_m \ dalam V} {argmax} P (w_1 \ dots w_n w_ {n + 1} \ dots w_m)$$

Tentu saja, memilah-milah $$$| V | ^ {m-n}, m = 1 \ dots M$ Tidak mungkin untuk memilih opsi terbaik untuk setiap permintaan yang masuk, jadi kami akan menggunakan Penelusuran Balok . Untuk model bahasa n-gram kami, diturunkan ke algoritme berikut:

def beam(initial, vocabulary): variants = [initial] for i in range(P): candidates = [] for variant in variants: candidates.extends(generate_candidates(variant, vocabulary)) variants = sorted(candidates)[:N] return candidates def generate_candidates(variant, vocabulary): top_terms = [] #         1, 2, ... n  for n0 in range(n): top_n = sorted(vocabulary, key=lambda c: P(|variant[-n0:]) top_terms.extends(top_n) candidates = [variant + [term] for term in top_terms] #       candidates = sorted(candidates, key=lambda v: P(variant))[:N] return candidates 

Di sini simpul yang disorot dengan warna hijau adalah opsi yang dipilih terakhir, angka di depan simpul $$$w_n$ - probabilitas $$$P (w_n | w_ {n-1})$ , setelah simpul - $$$P (w1 ... w_n)$ .

Ini telah menjadi jauh lebih baik, tetapi di generate_candidates Anda perlu dengan cepat mendapatkan N istilah terbaik untuk konteks yang diberikan. Dalam hal hanya menyimpan probabilitas n-gram, kita perlu membaca seluruh kamus, menghitung probabilitas semua frasa yang mungkin, dan kemudian mengurutkannya. Jelas, ini tidak akan berlaku untuk permintaan online.

Boron untuk probabilitas

Untuk mendapatkan varian probabilitas kondisional terbaik N dari kelanjutan frasa, kami menggunakan istilah boron. Dalam simpul $$$w_1 \ hingga w_2$ koefisien yang disimpan $$$\ alpha$ , nilai $$$P (w_2 | w_1)$ dan diurutkan berdasarkan probabilitas bersyarat $$$P (\ bullet | w_1 w_2)$ daftar istilah $$$w_3$ bersama dengan $$$P (w_3 | w_1 w_2)$ . Istilah khusus eos menandai akhir dari frasa.

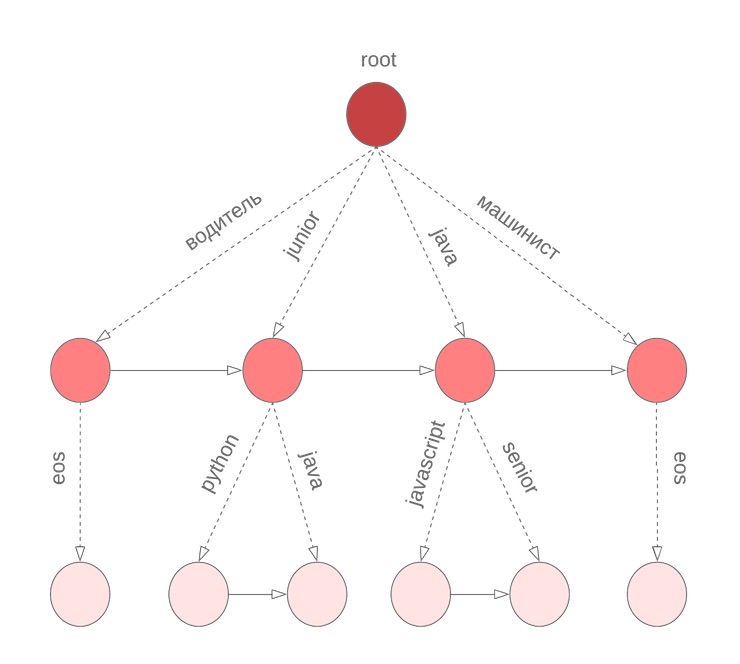
Namun ada nuansa

Dalam algoritme yang dijelaskan di atas, kami menganggap bahwa semua kata dalam kueri selesai. Namun, ini tidak benar untuk kata terakhir yang dimasuki pengguna saat ini. Kita lagi perlu menelusuri seluruh kamus untuk melanjutkan kata yang sedang dimasukkan. Untuk mengatasi masalah ini, kami menggunakan boron simbolis, di simpul yang kami simpan istilah M diurutkan berdasarkan probabilitas unigram. Misalnya, ini akan terlihat seperti bor kami untuk java, junior, jupyter, javascript dengan M = 3:



Kemudian, sebelum memulai Pencarian Beam, kami menemukan kandidat terbaik untuk melanjutkan kata saat ini $$$w_n$ dan pilih N kandidat terbaik untuk $$$P (w_1 \ dots w_n)$ .

Salah ketik

Kami telah membangun layanan yang memungkinkan Anda memberikan petunjuk yang baik untuk permintaan pengguna. Kami bahkan siap untuk kata-kata baru. Dan semuanya akan baik-baik saja ... Tetapi pengguna berhati-hati dan tidak mengganti keyboard hfcrkflre.

Bagaimana cara mengatasinya? Hal pertama yang terlintas dalam pikiran adalah mencari koreksi dengan menemukan opsi terdekat untuk jarak Damerau-Levenshtein, yang didefinisikan sebagai jumlah minimum penyisipan / penghapusan / penggantian karakter atau transposisi dari dua karakter tetangga yang diperlukan untuk mendapatkan yang lain dari satu baris. Sayangnya, jarak ini tidak memperhitungkan kemungkinan penggantian tertentu. Jadi, untuk kata yang dimasukkan "pencari ranjau", kita mendapatkan bahwa opsi "kolektor" dan "tukang las" adalah setara, meskipun secara intuitif tampaknya mereka berarti kata kedua.

Masalah kedua adalah bahwa kita tidak memperhitungkan konteks di mana kesalahan terjadi. Misalnya, dalam kueri "memesan sapper" kita harus tetap memilih opsi "kolektor" daripada "tukang las".

Jika Anda mendekati tugas mengoreksi kesalahan ketik dari sudut pandang probabilistik, wajar saja untuk sampai pada model saluran bising :

1. set alfabet $$$\ Sigma$ ;
2. set semua garis trailing $$$\ Sigma ^ *$ atas dirinya;
3. banyak baris kata yang benar $$$D \ subseteq \ Sigma ^ *$ ;
4. distribusi yang diberikan $$$P (s | w)$ dimana $$$s \ in \ Sigma ^ *, w \ dalam D$ .

Kemudian tugas koreksi ditetapkan sebagai menemukan kata yang benar untuk input s. Bergantung pada sumber kesalahan, ukur $$$P$ itu dapat dibangun dengan cara yang berbeda, dalam kasus kami adalah bijaksana untuk mencoba memperkirakan kemungkinan kesalahan ketik (sebut saja mereka penggantian elementer) $$$P_e (t | r)$ , di mana t, r adalah simbolik n-gram, dan kemudian mengevaluasi $$$P (s | w)$ sebagai probabilitas mendapatkan s dari w oleh penggantian elementer yang paling mungkin.

Biarkan $$$Part_n (x)$ - Memisahkan string x menjadi n substring (mungkin nol). Model Brill-Moore melibatkan perhitungan probabilitas $$$P (s | w)$ sebagai berikut:

$$

$$P (s | w) \ approx \ max_ {R \ di Part_n (w), T \ di Part_n (s)} \ prod_ {i = 1} ^ {n} P_e (T_i | R_i)$$

Tetapi kita perlu menemukannya $$$P (w | s)$ :

$$

$$P (w | s) = \ frac {P (s | w) P (w)} {P (s)} = const \ cdot P (s | w) \ cdot P (w)$$

Dengan belajar mengevaluasi P (w | s), kami juga akan menyelesaikan masalah pilihan peringkat dengan jarak Damerau-Levenshtein yang sama dan akan dapat mempertimbangkan konteks ketika mengoreksi kesalahan ketik.

Perhitungan $$$P_e (T_i | R_i)$

Untuk menghitung probabilitas substitusi dasar, kueri pengguna akan membantu kami lagi: kami akan membuat pasangan kata (s, w) yang

1. tutup di Damerau-Levenshtein;
2. salah satu kata lebih umum daripada N kali lainnya.

Untuk pasangan seperti itu, kami mempertimbangkan perataan optimal menurut Levenshtein:


Kami menyusun semua kemungkinan partisi s dan w (kami membatasi diri untuk panjang n = 2, 3): n → n, pr → rn, pro → rn, ro → po, m → ``, mm → m, dll. Untuk setiap n-gram, kami temukan

$$

$$P_e (t | r) = \ frac {count (r \ to t)} {count (r)}$$

Perhitungan $$$P (s | w)$

Perhitungan $$$P (s | w)$ langsung mengambil $$$O (2 ^ {| w | + | s |})$ : kita perlu memilah-milah semua kemungkinan partisi w dengan semua kemungkinan partisi s. Namun, dinamika pada awalan dapat memberikan jawaban $$$O (| w | * | s | * n ^ 2)$ dengan n adalah panjang maksimum pergantian unsur:

$$

$$d [i, j] = \ begin {case} d [0, j] = 0 & j> = k \\ d [i, 0] = 0 & i> = k \\ d [0, j] = P (s [0: j] \ spasi | \ spasi w [0]) & j <k \\ d [i, 0] = P (s [0] \ spasi | \ spasi w [0: i]) & i <k \\ d [i, j] = \ underset {k, l \ le n, k \ lt i, l \ lt j} {max} (P (s [jl: j] \ space | \ space w [ik: i]) \ cdot d [ik-1, jl-1]) \ end {cases}$$

Di sini P adalah probabilitas dari baris yang sesuai dalam model k-gram. Jika Anda melihat lebih dekat, ini sangat mirip dengan algoritma Wagner-Fisher dengan kliping Ukkonen. Di setiap langkah kita dapatkan $$$P (w [0: i] | s [0: j])$ dengan menyebutkan semua perbaikan $$$w [i-k: i]$ masuk $$$s [j-l: j]$ tunduk pada $$$k, l \ le n$ dan pilihan yang paling memungkinkan.

Kembali ke $$$P (w | s)$

Jadi, kita bisa menghitung $$$P (s | w)$ . Sekarang kita perlu memilih beberapa opsi dengan memaksimalkan $$$P (w | s)$ . Lebih tepatnya, untuk permintaan awal $$$s_1s_2 \ dots s_n$ kamu harus memilih $$$w_1 \ dots w_n$ dimana $$$P (w_1 \ dots w_n | s_1 \ dots s_n)$ maksimum. Sayangnya, pilihan opsi yang jujur ​​tidak sesuai dengan persyaratan waktu respons kami (dan batas waktu proyek hampir berakhir), jadi kami memutuskan untuk fokus pada pendekatan berikut:

1. dari kueri asli kami mendapatkan beberapa opsi dengan mengubah k kata-kata terakhir:
   
   1. kami memperbaiki tata letak keyboard jika istilah yang dihasilkan memiliki probabilitas beberapa kali lebih tinggi daripada yang asli;
   2. kami menemukan kata-kata yang jarak Damerau-Levenshtein tidak melebihi d;
   3. pilih dari mereka opsi top-N untuk $$$P (s | w)$ ;
2. kirim BeamSearch ke input bersama dengan permintaan asli;
3. saat memberi peringkat hasil, kami mendiskon opsi yang diperoleh $$$\ prod_ {i = 0} ^ {k-1} P (s_ {n-i} | w_ {n-i})$ .

Untuk item 1.2, kami menggunakan algoritma FB-Trie (maju dan mundur trie), berdasarkan pada pencarian fuzzy di pohon awalan maju dan mundur. Ini ternyata lebih cepat daripada mengevaluasi P (s | w) di seluruh kamus.

Statistik Kueri

Dengan konstruksi model bahasa, semuanya sederhana: kami mengumpulkan statistik tentang kueri pengguna (berapa kali kami membuat kueri untuk frasa tertentu, berapa banyak pengguna, berapa banyak pengguna terdaftar), kami memecah permintaan menjadi n-gram dan membangun bur. Lebih rumit dengan model kesalahan: setidaknya, kamus kata-kata yang tepat diperlukan untuk membangunnya. Seperti disebutkan di atas, untuk memilih pasangan pelatihan, kami menggunakan asumsi bahwa pasangan semacam itu harus dekat dalam jarak Damerau-Levenshtein, dan yang satu harus terjadi lebih sering daripada yang lainnya beberapa kali.

Tetapi datanya masih terlalu berisik: upaya injeksi xss, tata letak yang salah, teks acak dari clipboard, pengguna berpengalaman dengan permintaan "programmer c not 1c", permintaan dari kucing yang melewati keyboard .


Oleh karena itu, untuk menghapus sumber data, kami mengecualikan:

• istilah frekuensi rendah;
• Berisi operator bahasa query
• kosakata cabul.

Mereka juga memperbaiki tata letak keyboard, memeriksa kata-kata dari teks lowongan dan kamus terbuka. Tentu saja, itu tidak mungkin untuk memperbaiki semuanya, tetapi opsi seperti itu biasanya benar-benar terputus atau berada di bagian bawah daftar.

Dalam prod

Tepat sebelum perlindungan proyek, mereka meluncurkan layanan produksi untuk pengujian internal, dan setelah beberapa hari - untuk 20% pengguna. Di hh.ru, semua perubahan yang signifikan bagi pengguna harus melalui sistem tes AB , yang memungkinkan kami tidak hanya untuk memastikan signifikansi dan kualitas perubahan, tetapi juga untuk menemukan kesalahan .



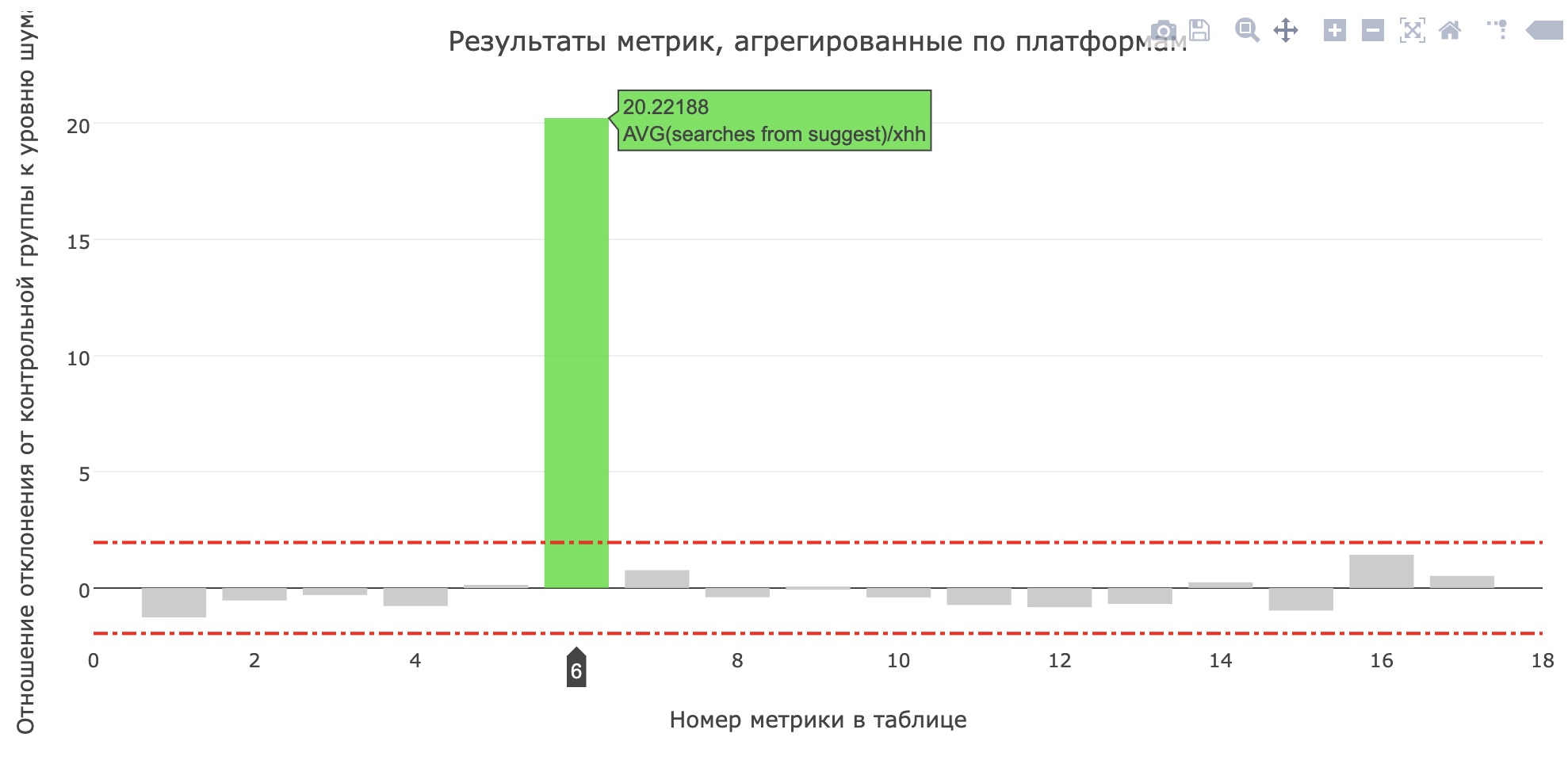
Metrik jumlah rata-rata pencarian dari sujest untuk pelamar telah meningkat (meningkat dari 0,959 menjadi 1,1355), dan bagian pencarian dari sujest dari semua permintaan pencarian telah meningkat dari 12,78% menjadi 15,04%. Sayangnya, metrik produk utama tidak bertambah, tetapi pengguna mulai menggunakan lebih banyak kiat.

Pada akhirnya

Tidak ada ruang untuk cerita tentang proses Sekolah, model yang diuji lainnya, alat yang kami tulis untuk perbandingan model, dan pertemuan di mana kami memutuskan fitur mana yang akan dikembangkan untuk mendapatkan demo perantara. Lihatlah catatan sekolah masa lalu , tinggalkan permintaan di https://school.hh.ru , selesaikan tugas yang menarik dan datang untuk belajar. Ngomong-ngomong, layanan untuk pengecekan tugas juga dilakukan oleh lulusan set sebelumnya.

Apa yang harus dibaca?

1. Pengantar Model Bahasa
2. Model Brill-Moore
3. Fb-trie
4. Apa yang terjadi pada permintaan pencarian Anda