Apa yang harus Anda lakukan jika Anda perlu menggambar grafik, tetapi alat-alat yang berada di bawah lengan Anda menggambar semacam gumpalan rambut atau bahkan melahap semua RAM dan menggantung sistem? Selama beberapa tahun terakhir bekerja dengan grafik besar (ratusan juta simpul dan tepi), saya telah mencoba banyak alat dan pendekatan, dan hampir tidak menemukan ulasan yang layak. Oleh karena itu, sekarang saya menulis ulasan sendiri.
Mengapa memvisualisasikan grafik sama sekali?
Temukan apa yang harus dicari
Pada input, kami biasanya hanya memiliki satu set simpul dan tepi, yang pada dasarnya adalah grafik. Kami dapat menghitung beberapa karakteristik statistik, grafik metrik dari itu, tetapi ini tidak akan memberi Anda gambaran yang jelas tentang apa itu. Visualisasi yang baik dapat menunjukkan apakah cluster memiliki jembatan atau jembatan, atau homogen, atau mungkin bergabung menjadi satu benjolan ke beberapa pusat daya tarik utama.
Membanggakan tentang
Visualisasi data, menurut definisi, memecahkan masalah representasi. Jika beberapa pekerjaan telah dilakukan, maka Anda dapat menunjukkan kesimpulan dalam gambar yang spektakuler. Misalnya, jika Anda melakukan pengelompokan grafik, Anda dapat mewarnai grafik dalam kelompok dan menunjukkan bagaimana label berbeda terkait satu sama lain.
Dapatkan tanda
Terlepas dari kenyataan bahwa algoritma visualisasi grafik terutama dikembangkan hanya sebagai alat untuk mendapatkan gambar, mereka dapat digunakan sebagai metode untuk mengurangi dimensi. Grafik itu sendiri, jika diwakili oleh matriks adjacency, adalah data dalam ruang dimensi tinggi, dan ketika rendering, kita mendapatkan dua koordinat untuk setiap simpul (kadang-kadang tiga atau lebih, tetapi ini merupakan pengecualian). Kedekatan simpul dalam visualisasi sering mengungkapkan kesamaan dalam sifat.
Apa masalah dengan grafik besar?
Dengan grafik besar yang saya maksud adalah dimensi, katakanlah, mulai dari 10 ribu simpul atau tepian. Untuk ukuran yang lebih kecil, biasanya tidak ada masalah, karena hampir semua alat yang dapat ditemukan dengan pencarian cepat di Internet pada dasarnya menyelesaikan masalah mereka dengan baik untuk volume seperti itu. Apa yang salah dengan grafik besar? Dua masalah: ini keterbacaan dan kecepatan. Diharapkan bahwa semakin banyak objek, semakin sulit untuk menavigasi mereka. Untuk grafik besar, gambar sering diperoleh yang tidak mungkin dimengerti. Selain itu, algoritma grafik umumnya sangat lambat, banyak memiliki kompleksitas algoritme yang sebanding dengan kuadrat (terkadang kubus) dari jumlah simpul dan / atau tepi. Bahkan jika Anda menunggu rendering, Anda masih tidak mampu untuk melewati banyak opsi untuk mendapatkan hasil yang memuaskan.
Apa yang ditulis oleh orang pintar yang berbeda tentang ini?
Ada beberapa karya yang ingin saya perhatikan:
[1] Helen Gibson, Joe Faith dan Paul Vickers: "Sebuah survei teknik tata letak grafik dua dimensi untuk visualisasi informasi"Para pria pertama-tama memilah pendekatan apa yang ada untuk menggambar grafik, menjelaskan prinsip-prinsip pekerjaan, dan kemudian mencoba untuk mencoba semuanya. Ada tabel yang sangat terperinci dengan informasi tentang berbagai algoritma, termasuk kompleksitas algoritmanya.
[2] Oh-Hyun Kwon, Tarik Crnovrsanin dan Kwan-Liu Ma “Seperti apa Grafik di Layout Ini? Pendekatan Pembelajaran Mesin untuk Visualisasi Grafik Besar ”Di sini, kawan-kawan kami menjadi sangat bingung dan mendapatkan semua implementasi algoritma visualisasi grafik yang mereka bisa. Kemudian mereka memvisualisasikan banyak grafik dan memberi tanda untuk markup. Menurut hasil, kami mengajarkan model untuk mengevaluasi seperti apa grafiknya pada opsi gaya yang berbeda. Saya mengambil beberapa gambar dari artikel ini.
Teori
Penumpukan adalah cara untuk memetakan koordinat ke setiap titik grafik. Biasanya kita berbicara tentang koordinat di pesawat, meskipun secara umum tidak harus pesawat. Cukup menggunakan lebih dari 2 dimensi hampir tidak pernah diperlukan.
Apa itu style yang bagus?

Sangat mudah untuk mengatakan bahwa sesuatu terlihat baik atau buruk, tetapi sulit untuk menjelaskan kepada mesin bagaimana memberikan penilaian seperti itu. Untuk membuat gaya "baik", apa yang disebut metrik "estetika" biasanya dioptimalkan, yang dirumuskan lebih objektif. Inilah beberapa di antaranya:
Minimum Rib CrossingSederhana: ketika ada banyak persimpangan, ternyata "bubur", ketika kecil, maka gambar terlihat "lebih bersih"
Puncak yang berdekatan berdekatan satu sama lain, tidak berdekatan jauh.Grafik menurut definisi adalah satu set koneksi antara simpul dan satu set simpul. Membuat simpul terhubung lebih dekat satu sama lain adalah cara langsung dan logis untuk mengekspresikan sifat dasar data grafik.
Komunitas dikelompokkanIni mengikuti dari paragraf sebelumnya. Jika ada banyak node yang lebih terhubung satu sama lain daripada dengan seluruh grafik, mereka membentuk "komunitas" dan dalam gambar akan terlihat seperti cluster yang padat
Hamparan minimum dari simpul dan tepiCukup jelas. Jika kita tidak dapat melihat satu atau beberapa objek di sini, maka visualisasinya buruk dibaca.
Mendistribusikan simpul dan / atau tepi secara merataKondisi ini berguna jika properti grafik tidak memungkinkan untuk melihat setidaknya beberapa struktur. Sebagai contoh, jika kita memiliki seluruh grafik - itu adalah satu cluster padat, maka lebih baik untuk mengoleskannya pada gambar untuk melihat setidaknya ketidakrataan koneksi daripada membiarkannya bergabung menjadi satu tempat padat.
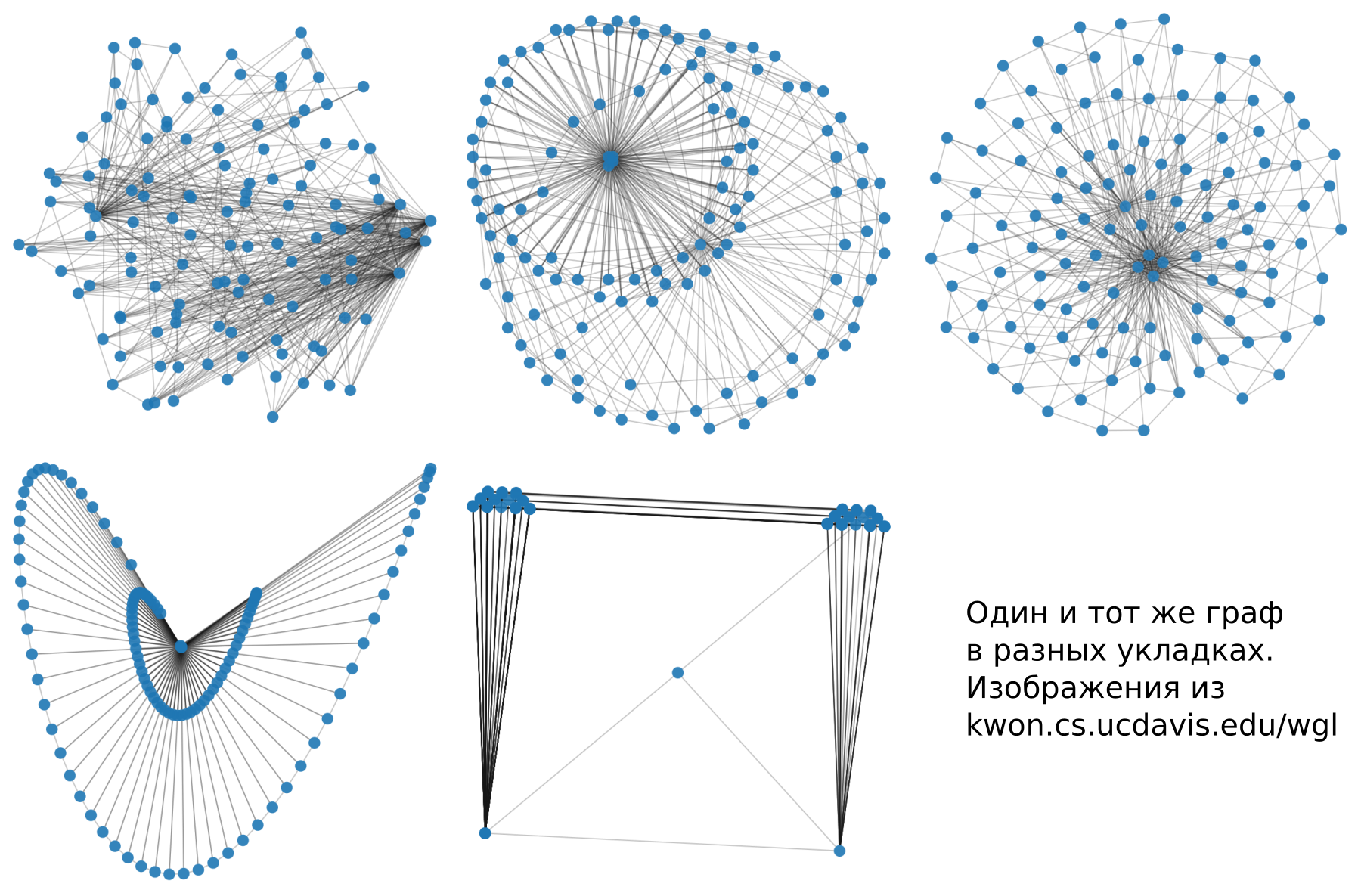
Apa saja penataannya
Saya menganggap penting untuk mempertimbangkan ketiga jenis penataan ini, walaupun ada banyak klasifikasi dan jenis. Namun, pengetahuan jenis ini cukup untuk menavigasi subjek.
- Diarahkan secara paksa dan Berbasis Energi
- Pengurangan Dimensi
- Fitur Simpul
Diarahkan dengan Kekuatan dan Berbasis Energi
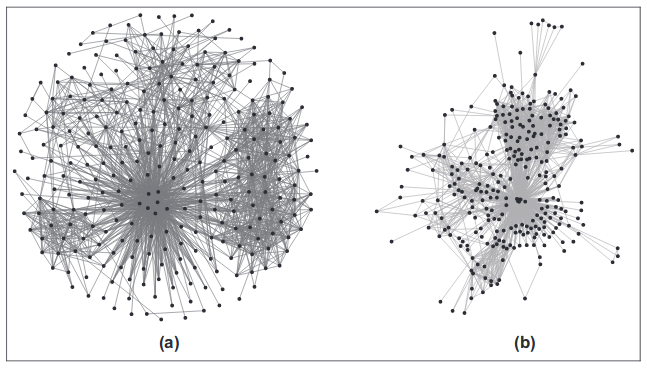
Metode ini menggunakan simulasi kekuatan fisik. Puncak diwakili sebagai partikel bermuatan yang saling tolak, dan ujung - sebagai tali elastis yang menyatukan puncak yang berdekatan. Kemudian, pergerakan simpul dalam sistem seperti itu disimulasikan sampai kondisi mapan tercapai. Pendekatan lain mencoba menggambarkan energi potensial dari sistem tersebut dan menemukan posisi simpul yang sesuai dengan minimum.
Kelebihan dari keluarga algoritma ini sebagai gambar. Biasanya diperoleh style yang sangat bagus yang mencerminkan topologi grafik. Kontra di antara parameter yang perlu dikonfigurasi. Baik dan, tentu saja, kompleksitas komputasi. Untuk setiap simpul, Anda perlu menghitung gaya yang bekerja dari semua simpul lainnya.
Algoritma keluarga penting adalah Force Atlas, Fruchterman-Reingold, Kamada Kawaii, dan OpenOrd. Algoritma terakhir menggunakan optimasi rumit, misalnya, memotong tepi panjang untuk mempercepat perhitungan, dan sebagai efek samping, lebih banyak kumpulan padat dari puncak dekat diperoleh.
Pengurangan Dimensi

Grafik dapat didefinisikan oleh matriks adjacency, yaitu oleh matriks kuadrat NxN, di mana N adalah jumlah simpul. Ini dapat diartikan sebagai objek N dalam ruang dimensi N. Representasi ini memungkinkan penggunaan metode universal mengurangi dimensi, seperti tSNE, UMAP, PCA, dan sebagainya. Pendekatan lain didasarkan pada penghitungan jarak teoretis antar simpul, berdasarkan bobot tepi dan pengetahuan topologi lokal, dan kemudian mencoba mempertahankan hubungan antara jarak-jarak ini ketika bergerak ke ruang-ruang dimensi yang lebih kecil.
Layout Berbasis Fitur

Biasanya data berasal dari dunia nyata, di mana kita tidak hanya memiliki informasi tentang kedekatan verteks. Puncak adalah beberapa benda nyata dengan propertinya sendiri. Mengingat ini, kita dapat menggunakan properti dari simpul untuk menampilkannya di pesawat. Untuk melakukan ini, Anda bisa menggunakan pendekatan apa pun yang biasa digunakan untuk data tabular. Ini adalah metode mengurangi dimensi PCA, UMAP, tSNE, Autoencoders yang telah disebutkan di atas. Atau Anda dapat menggambar plot sebar sederhana (plot sebar) untuk pasangan fitur dan menggambar tepi sudah di atas tampilan yang dihasilkan. Secara terpisah, kita dapat menyebutkan Hive Plot - metode yang menarik ketika nilai-nilai atribut sesuai dengan sumbu yang berbeda diarahkan dari pusat, di mana simpul berada, dan ujung-ujungnya digambar dengan lengkok di antara mereka.
Alat Visualisasi Grafik Besar

Terlepas dari kenyataan bahwa tugas visualisasi sudah tua dan relatif populer, ada masalah besar dengan alat untuk grafik besar. Sebagian besar dari mereka tidak didukung. Hampir setiap orang memiliki beberapa kekurangan serius, yang harus diatasi. Saya hanya akan berbicara tentang hal-hal yang layak disebutkan dan dapat digunakan untuk grafik besar. Untuk grafik kecil, tidak ada masalah - alatnya mudah ditemukan dan pada dasarnya berfungsi dengan baik.
GraphViz

Transaksi dan alamat Bitcoin blockchain hingga 2011

Mengonfigurasi pengaturan bisa jadi sulit
Alat CLI sekolah tua dengan bahasa deskripsi grafiknya sendiri - titik. Bahkan, ini adalah paket dengan gaya berbeda untuk setiap kesempatan. Untuk grafik besar, ada alat sfdp - ia termasuk dalam kelas penumpukan Force Directed. Kelebihan dan kekurangan alat ini dalam meluncurkan dari baris perintah. Ini sangat nyaman untuk reproduktifitas dan otomatisasi, namun, tanpa slider dan menampilkan hasil antara, pengaturan parameter menjadi sangat menyakitkan. Kami mengatur parameter, mulai, tunggu tanpa progress bar, lihat hasilnya, ubah parameter, restart. Mampu menulis dalam format svg, png dan gambar lainnya.
Gephi
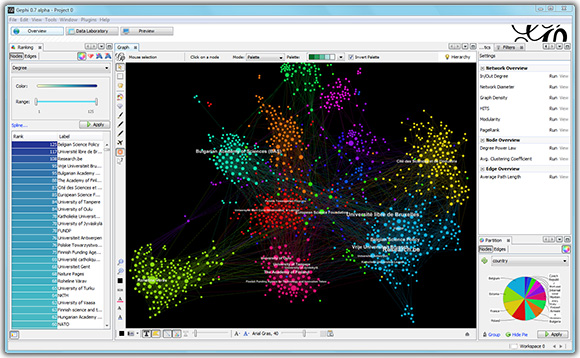

Rekomendasi 173 ribu film dengan iMDB

Beberapa juta puncak sudah merupakan tugas yang terlalu sulit
Mungkin alat yang paling kuat secara keseluruhan. Ini adalah aplikasi GUI yang berisi serangkaian gaya dasar, serta banyak alat analisis grafik lainnya. Komunitas gephi telah menulis banyak plugin, seperti Multigravity Force-Atlas 2 favorit saya atau sebuah plugin untuk mengekspor gaya ke halaman web interaktif. Juga, implementasi OpenOrd asli terkandung dalam Gephi. Gephi memiliki alat untuk melukis simpul dan tepi sesuai dengan propertinya, mengatur keterangan, ukuran, dan opsi render lainnya. Ada ekspor ke format gambar utama, termasuk vektor.
Fakta yang sangat menjengkelkan adalah bahwa Gephi telah ditinggalkan selama beberapa tahun. Kedua pengembang utama, tidak memiliki sumber daya untuk mentransfer pengetahuan mereka yang diperlukan untuk pengembangan lebih lanjut kepada orang lain, mengatakan bahwa mereka tidak lagi dapat secara aktif mendukung Gephi. Kerugian lainnya termasuk "oakiness" tertentu dari antarmuka, dan kurangnya fitur yang jelas, tetapi tidak ada "hanya lebih baik," tidak ada yang menulis. Dari berita terbaru, sebuah pernyataan muncul di blog proyek bahwa kekuatan WebGL modern sudah menyalip Gephi lama dan ada peluang untuk melihatnya dilahirkan kembali sebagai aplikasi web.
igraph

Grafik rekomendasi musik dalam lastfm. Sumbernya ada di
sini .
Seseorang tidak bisa tidak membayar upeti kepada paket keperluan umum ini untuk analisis grafik. Salah satu visualisasi grafik paling spektakuler pada masanya dibuat oleh salah satu penulis igraph. Dia mengembangkan gaya DrL untuk ini. Itu adalah grafik rekomendasi dari band lastfm. Hasilnya lebih tinggi.
Kerugiannya termasuk dokumentasi yang menjijikkan. Setidaknya ke api python. Lebih mudah untuk membaca sumbernya segera.
LargeViz
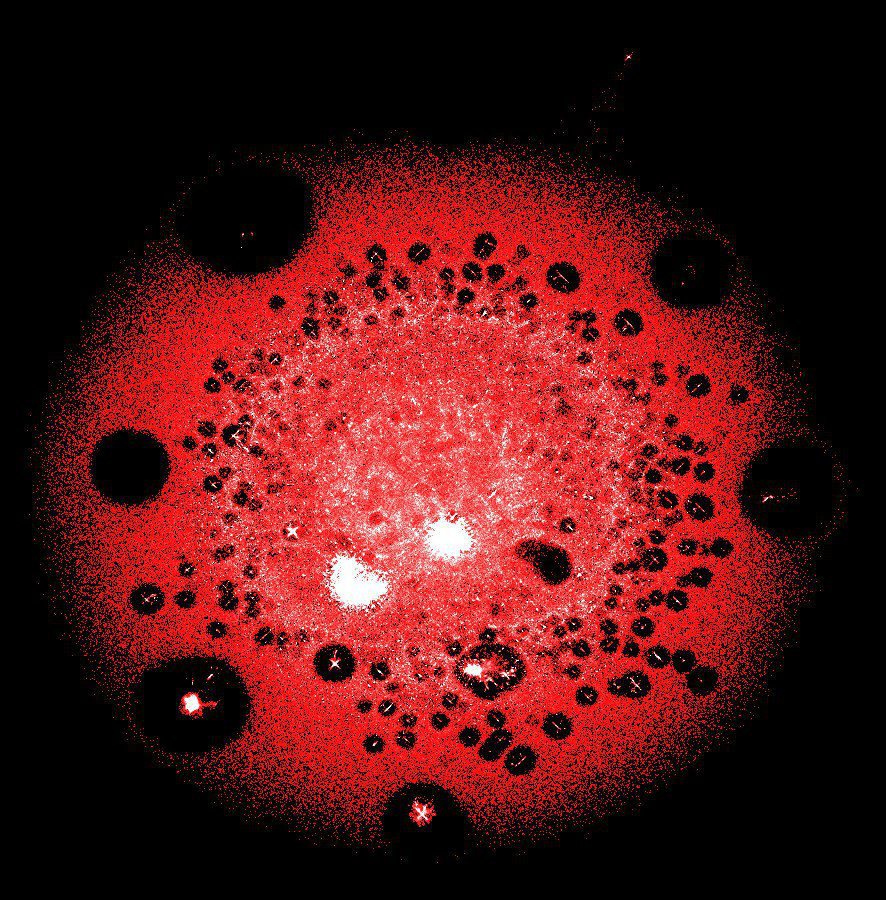
Beberapa puluh juta puncak (transaksi dan alamat) di salah satu kelompok terbesar dari blockchain Bitcoin
Keselamatan nyata saat Anda perlu menggambar grafik raksasa. LargeViz mengacu pada algoritma reduksi dimensi dan dapat digunakan tidak hanya untuk grafik, tetapi juga untuk data tabel acak. Ia bekerja dari baris perintah dan memiliki kinerja yang sangat baik. Sangat hemat dalam memori dan cepat.
Grafik

Alamat yang dapat diretas dalam seminggu, dan transaksinya

Antarmuka yang jelas, tetapi sangat terbatas, pengaturan standar yang masuk akal
Satu-satunya alat komersial dalam daftar ini. Graphistry adalah layanan yang mengambil data Anda dan melakukan perhitungan berat di sisinya. Klien hanya melihat gambar yang indah di browser. Sebenarnya, gephi tidak lebih baik dari opsi default yang wajar dan interaktivitas. Ini hanya menerapkan satu gaya: sesuatu yang mirip dengan ForceAtlas. Ada batas 800 ribu untuk jumlah simpul atau tepi maksimum.
Grafik Embeddings
Untuk ukuran gila, ada juga pendekatan. Sudah dimulai dengan sejuta simpul, ketika menggambar, masuk akal untuk melihat hanya kepadatan dari berbagai titik di ruang, hanya karena tidak ada yang bisa dilihat. Sebagian besar algoritma yang ditemukan secara khusus untuk rendering grafik akan bekerja selama puluhan juta simpul atau tepi selama berjam-jam, jika tidak berhari-hari. Anda dapat keluar dari situasi ini dengan menyelesaikan masalah yang sedikit berbeda. Ada banyak metode untuk mendapatkan representasi vektor dari dimensi yang diberikan, yang mencerminkan sifat-sifat simpul grafik. Setelah menerima representasi seperti itu, itu hanya mengurangi dimensi menjadi 2 untuk mendapatkan gambar sudah.
Node2Vec

Node2Vec + UMAP
Mengadaptasi word2vec biasa untuk grafik. Alih-alih urutan kata-kata, urutan simpul diambil untuk traversal acak grafik dan dikirim ke word2vec bukan kata-kata. Metode hanya memperhitungkan informasi tentang lingkungan simpul. Ini biasanya sudah cukup.
Ayat
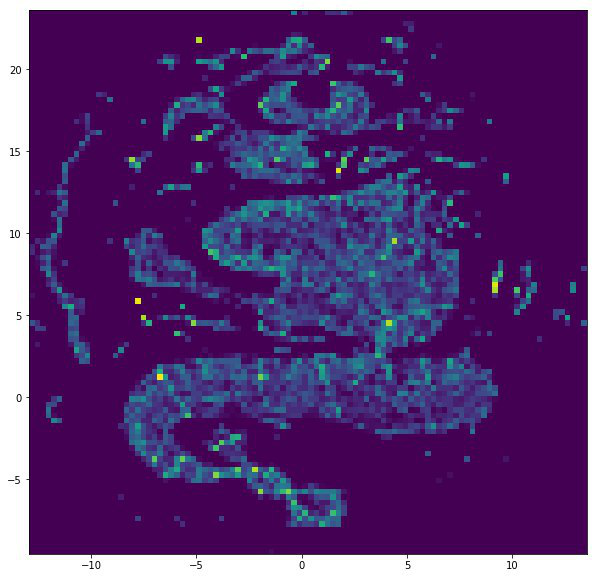
VERSE + UMAP
Algoritma canggih untuk mendapatkan embedding grafik, yang berupaya mendapatkan representasi serbaguna untuk simpul, yaitu, memperhitungkan semua peran yang dibutuhkan sebuah simpul dalam grafik. Lingkungan simpul dan topologi lokal grafik diperhitungkan.
Konvolusi grafik

Konvolusi Grafik + Autoencoder
Ada banyak cara untuk menentukan operasi konvolusi pada grafik, tetapi pada dasarnya ini adalah "pengolesan" informasi pada grafik, sehingga simpul menerima informasi tentang tanda-tanda tetangga mereka. Anda dapat menambahkan informasi topologi lokal ke atribut ini.
Bonus: lebih banyak tentang konvolusi grafik
Semua pendekatan yang dijelaskan didasarkan pada beberapa alat yang sudah jadi. Kasus terakhir adalah pengecualian. Untuk mengimplementasikan konvolusi grafik, Anda perlu berpikir sedikit dan menulis sedikit kode.
Analisis terperinci tentang konvolusi pada grafik dan data non-Euclidean lainnya adalah topik yang layak untuk artikel terpisah. Di sini saya akan menjelaskan pendekatan dasar paling sederhana, yang tidak memerlukan kerangka grafik khusus dan mudah diskalakan. Jadi, kami ingin tanda-tanda setiap simpul grafik berisi informasi tentang tanda-tanda tetangga.
Bagaimana kita melakukan ini?
Cara yang paling jelas adalah dengan mengambil rata-rata tetangga. Jika Anda berpikir lebih banyak tentang apa yang terjadi dan informasi apa yang rata-rata hilang, Anda dapat menambahkan statistik lain di sana, seperti standar deviasi, minimum, maksimum, dan sebagainya.
Bagaimana cara mengaturnya sekarang? Untuk memulainya, grafik pada dasarnya adalah banyak simpul dan banyak sisi. Kami hanya tertarik pada bagian-bagian yang terhubung dari lebih dari satu titik, sehingga daftar tepi dalam kasus kami sepenuhnya menentukan grafik. Ini ditulis dengan mudah dalam bentuk tabel: di kolom pertama, simpul-simpul dari mana ujung keluar, di kolom kedua, tempat tepi-tepi ini masuk. Selanjutnya kita perlu membaca statistik. Ini adalah tugas yang sangat umum dan karena itu Anda dapat menggunakan kerangka kerja di mana semuanya dioptimalkan hingga kami.
Kekuatan kerangka tabel dalam analisis grafik
Kami sampai pada kesimpulan bahwa kami memiliki piringan yang menentukan grafik dan kami perlu membaca statistik untuk beberapa jumlah. Tabel dan statistik - semua ini ada dalam panda, jadi berikut ini akan menjadi contoh implementasi di dalamnya.
Untuk memulai, mari kita atur grafik:
ara = np.arange(101).reshape(-1, 1) sample = np.vstack((np.hstack((ara[:-1], ara[1:])),
Ini hanya rantai 101 simpul yang terhubung satu sama lain, seperti pada gambar.

Kemudian kita mengatur tanda-tanda simpul secara acak:
feats = np.random.normal(size=(101, 10))
Dan kami akan membuat kerangka data panda dari ini semua:
edges = pd.DataFrame(sample, columns=['source', 'target']) cols = ['col{}'.format(i) for i in range(10)] feats = pd.DataFrame(feats, columns=cols) feats['target'] = ara
Sekarang kita mengatur fungsi konvolusi itu sendiri:
def make_conv(edges, feats, cols, by, on, size=1000000, agg_f='mean', prefix='mean_'): """ edges -- edgelist: pandas dataframe with two columns (arguments by and on) feats -- features dataframe with key column (argument on) and features columns (argument cols) by -- column in edges to be used as source nodes on -- column in edges to be used as neighbor nodes size -- number of unique source nodes to be used in one chunk agg_f -- can be interpreted as pooling function. Pandas has several optimised functions for basic statistics, that can be passed as string arg (see pandas docs), but you also can provide any function you like prefix -- prefix for new column names """ res_feats = []
Apa yang terjadi di sini
Pertama, kami memilih sepotong simpul yang akan kami buat konvolusi, mengambil semua tepinya, menyatukannya dengan tanda-tanda tetangga dan menulisnya ke kerangka data temp. Kemudian kita kelompokkan dengan simpul dari sumber, dan agregat menggunakan fungsi agg_f, yang secara sederhana rata-rata. Tambahkan hasil untuk bagian saat ini ke daftar, dan pada akhirnya hanya menyatukan hasilnya.

Untuk grafik ini, akan terlihat seperti ini
Kami menerapkan fungsi dan menggambar hasilnya:
conv1 = make_conv(edges, feats, cols, 'source', 'target') plt.figure(figsize=(3, 8)) plt.imshow(np.hstack((feats[cols].values, conv1.values[:, 1:])), cmap='jet');

Tanda-tanda awal, kemudian yang asli dan hasil dari konvolusi pertama, kemudian yang asli dan hasil dari dua konvolusi.
Misalnya, kasus sederhana semacam itu dipilih secara khusus sehingga mudah untuk melihat secara visual bagaimana tanda-tanda itu "dioleskan" pada tetangga jika Anda secara langsung menggambar matriks tanda-tanda. Dalam kasus yang lebih umum, prosesnya terlihat seperti ini:

Jika Anda ingin sedikit lebih banyak matematika
Jika Anda pernah mendengar tentang konvolusi grafik sebelumnya, maka kemungkinan besar itu berada dalam konteks jaringan konvolusi grafik (Graph Convolutional Networks - GCN). Bagi sebagian orang, trik dengan tablet yang dijelaskan di sini mungkin tampak "tidak sulit." Bahkan, satu artikel yang sangat menarik dikhususkan untuk penggunaan konvolusi grafik tanpa pembelajaran mendalam: "Penyederhanaan Grafik Jaringan Konvolusional". Ini memberikan definisi konvolusi
dimana
Merupakan matriks fitur, dan
Adalah Laplacian yang dinormalisasi dari grafik, yang didefinisikan seperti ini:
disini
Apakah matriks adjacency dari grafik disimpulkan dengan matriks identitas, dan
- matriks di diagonal di mana derajat simpul grafik direkam. Dan semua ini ditulis dalam beberapa baris dalam python menggunakan scipy dan numpy:
S = sparse.csgraph.laplacian(adj, normed=True) feats_conv = S @ feats
Di sini sparse adalah modul di dalam scipy untuk bekerja dengan matriks sparse, adj adalah matriks adjacency, dan feats dan feats_conv adalah tanda-tanda sebelum dan sesudah konvolusi. Pendekatan ini lebih teliti, tetapi skalanya sangat buruk. Selain itu, jika Anda berpikir sedikit tentang arti dari apa yang terjadi, maka ini setara dengan perbedaan antara nilai fitur pada titik dan rata-rata di tetangga titik, yaitu, itu dapat sepenuhnya diselesaikan dengan skema sebelumnya dengan tabel, jika Anda menambahkan satu operasi.
Referensi
Ulasan Visualisasi Grafikleonidzhukov.net/hse/2018/sna/papers/gibson2013arxiv.org/pdf/1710.04328.pdfPenyederhanaan Grafik Jaringan Konvolusionalarxiv.org/pdf/1902.07153.pdfGraphVizgraphviz.orgGephigephi.orgigraphigraph.orgLargeVizarxiv.org/abs/1602.00370github.com/lferry007/LargeVisGrafikwww.graphistry.comNode2Vecsnap.stanford.edu/node2vecgithub.com/xgfs/node2vec-cAyattsitsul.in/publications/versegithub.com/xgfs/verseNotebook dengan kode paket panda penuhgithub.com/iggisv9t/graph-stuff/blob/master/Universal%20Convolver%20Example.ipynbKonvolusi grafikBerikut adalah karya-karya yang dikumpulkan pada jaringan konvolusi grafik:
github.com/thunlp/GNNPapersInti dari keseluruhan artikel dalam satu tabel