Representasi batas (B-rep) adalah metode utama untuk mewakili objek yang dimodelkan di sebagian besar kernel geometris, termasuk kernel C3D Modeler kami. Algoritma inti yang mengedit model, seperti menerapkan operasi fillet, melakukan operasi pemotongan, dan mendapatkan proyeksi datar membutuhkan ketelitian representasi B-rep. Variasi data 3D yang berkembang pesat dalam format poligon membuat tugas transformasi model dari poligon menjadi representasi batas semakin relevan. Sebagai hasilnya, kami mengembangkan SDK baru, C3D B-Shaper, yang merupakan bagian dari C3D Toolkit kami.



Menggunakan algoritma triangulasi (dikenal sebagai tessellation) pada representasi batas model relatif mudah. Membangun representasi poligon (tessellated) berguna untuk tujuan visualisasi dan untuk melakukan perhitungan geometrik.

Namun transformasi terbalik - dari representasi poligon ke B-rep - menghadapi serangkaian masalah terkait dengan kompleksitas dalam mengenali berbagai jenis permukaan, termasuk yang berbentuk bebas. Juga, ada masalah kebisingan dalam model poligonal yang muncul secara khas sebagai hasil pemindaian 3D.

Proses umum dimana C3D B-Shaper mengubah model dari format poligonal ke B-rep terdiri dari tiga tahap: segmentasi, rekonstruksi permukaan, dan konstruksi model b-rep. Proses transformasi bersifat berulang: jika pengguna dengan alasan apa pun tidak senang dengan hasilnya, maka koreksi dapat dilakukan selama tahap segmentasi dan rekonstruksi permukaan.


Mengubah representasi poligon menjadi B-rep

Namun, sebelum memulai proses transformasi b-rep, kami meningkatkan kualitas mesh poligon sumber dengan menerapkan perbaikan berikut: mengoordinasikan arah normal dalam poligon yang berdekatan; menghilangkan lubang; dan menerapkan algoritma perataan ke sumber mesh yang bising, jika ada.

Segmentasi model poligonal

Tahap pertama transformasi adalah segmentasi model poligonal. Kami mengklasifikasikan poligon jala ke dalam himpunan bagian (segmen). Informasi tentang normals pada setiap vertex mesh memungkinkan untuk melakukan segmentasi orde pertama dan kemudian melakukan pemisahan mesh awal, serta mengklasifikasikan area sebagai datar atau sangat melengkung. Pemisahan mesh awal didasarkan pada mendefinisikan tepi "tajam". Ini adalah tepi antara dua poligon segitiga di mana sudut antara normalnya rata-rata melebihi nilai yang telah ditentukan.

Segmentasi orde kedua menganalisis mesh berdasarkan kelengkungan utamanya, yang cukup untuk mengklasifikasikan permukaan dasar. Ketika menghitung kelengkungan pada simpul jala, kami menggunakan hasil karya Meyer (Mark Meyer, Mathieu Desbrun, Peter Schroder, dan Alan H. Barr, "Operator Geometri Diferensial-Diskrit untuk Triangulasi 2-Manifold," Visualisasi dan Matematika III, 2003) dalam mendefinisikan operator diferensial diskrit untuk daerah triangulasi: satu set simpul yang berdekatan (terkait dengan simpul yang diberikan melalui tepi) dipertimbangkan untuk setiap simpul mesh awal. Selanjutnya, operator diskrit K dihitung untuk simpul tersebut. Berdasarkan pada operator, rata-rata kelengkungan normal, rata-rata K _H , dan Gaussian K _G ditentukan pada vertex mesh.


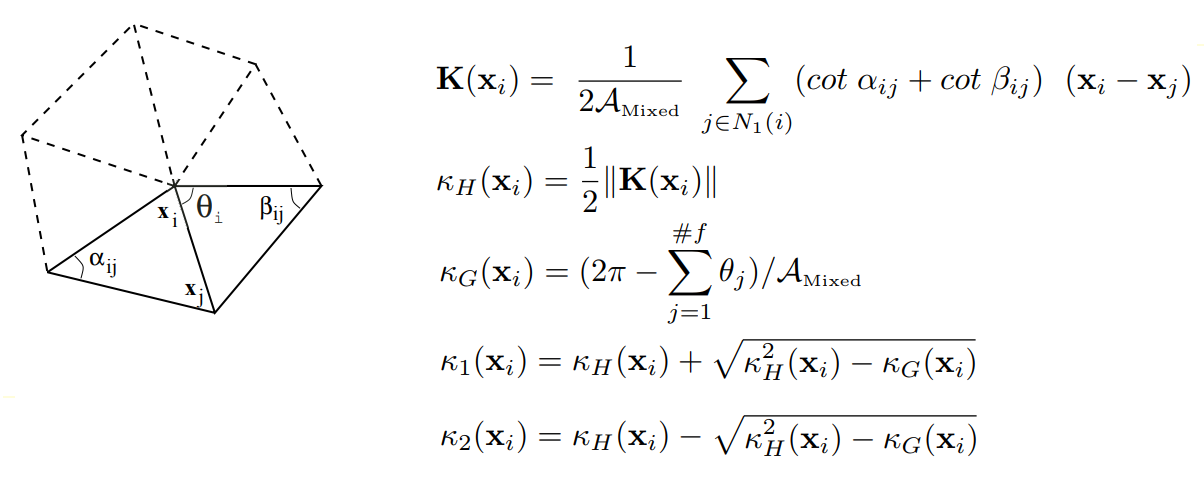Menentukan operator diferensial diskrit untuk wilayah triangulasi

Dengan cara ini tensor kelengkungan dihitung untuk setiap simpul mesh, dari mana nilai kelengkungan utama K ₁ dan K ₂ dan arah kelengkungan utama diekstraksi.

Verteks mesh diklasifikasikan berdasarkan nilai-nilai lengkungan utama mereka K ₁ dan K ₂ , dan kemudian dihitung untuk mereka. Algoritma klasifikasi vertex didasarkan pada k-means, yaitu, meminimalkan deviasi kuadrat total dari titik-titik cluster dari pusat-pusat cluster. Output yang dihasilkan dari algoritma berisi simpul jala terkait dengan sebuah cluster $$$Ci$dan sepasang kelengkungan (cluster-center - L. Guillaume, "Segitiga Berbasis Kelengkungan Tensor Berbasis Segitiga dengan Boundary Rectification," Prosiding Computer Graphics International (CGI), 2004).


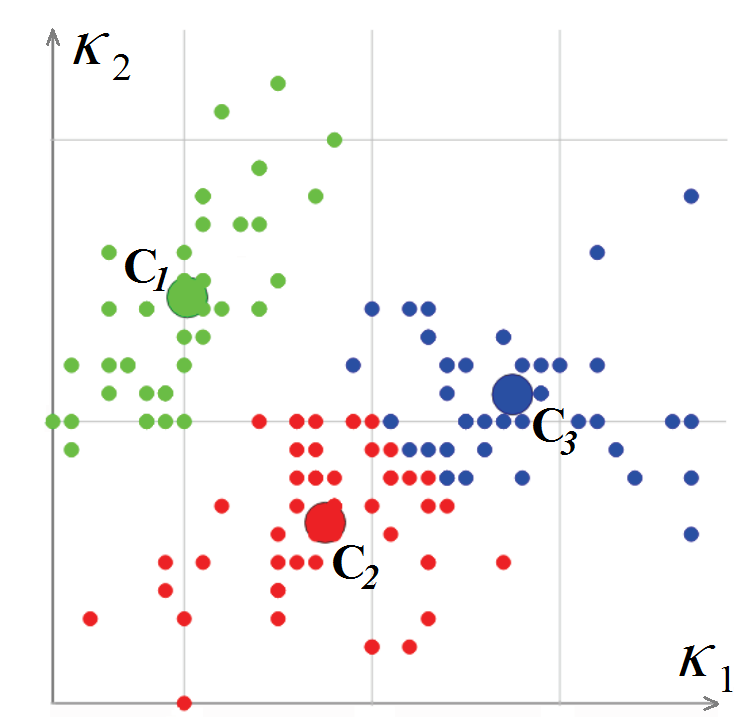Mengklasifikasikan simpul poligonal dalam ruang kelengkungan

Setelah kita selesai mengklasifikasikan simpul poligon, kita pergi ke mengklasifikasikan poligon. Untuk memulai prosedur ini, kami memilih poligon segitiga yang kelengkungannya dapat dipertimbangkan sepenuhnya. Ini adalah salah satu yang memiliki tiga simpul dalam satu cluster, atau memiliki dua simpul pada sisi yang tajam. Poligon dilabeli sebagai segmen baru dan menjadi titik awal untuk prosedur rekursif yang memperluas segmen: untuk setiap poligon segitiga, poligon yang berdekatan dianggap sepanjang tepi di antara keduanya tidak "tajam." Ketika simpul poligon yang berdekatan, yang berlawanan dengan tepi yang sama, berada di tepi yang tajam atau milik cluster yang sama, poligon ditambahkan ke segmen. Proses ini diulang sampai semua poligon yang membentuk mesh hilang.


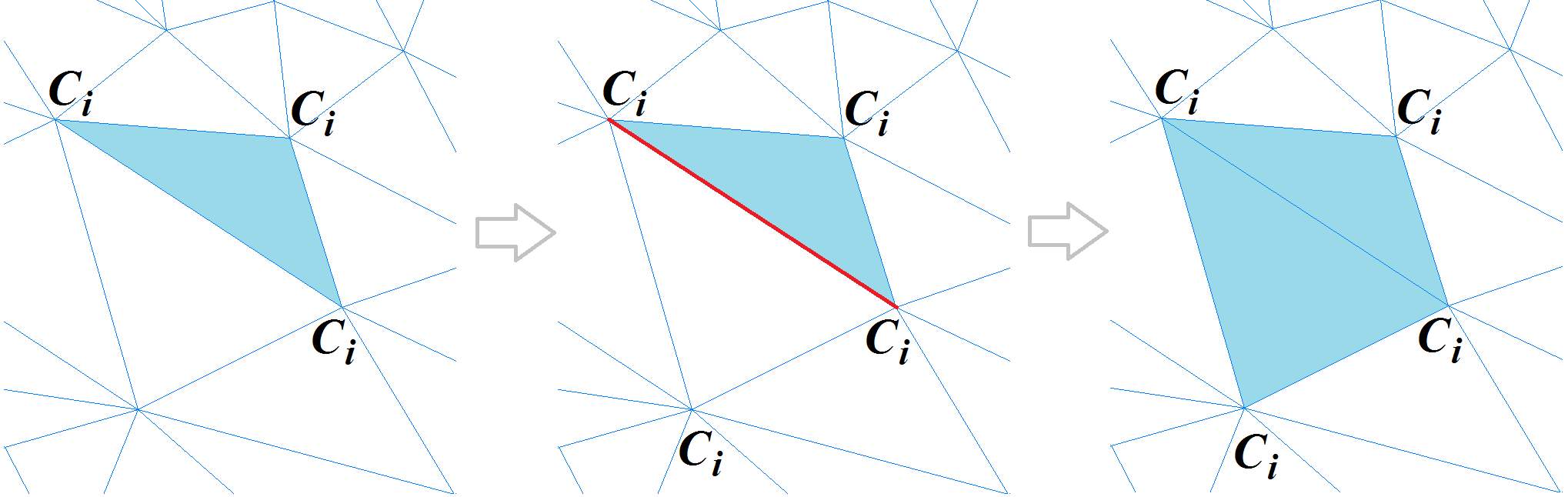Segmentasi mesh poligonal

Setelah prosedur pembuatan segmen selesai, algoritma lain menjahit segmen yang berdekatan bersama-sama untuk menghilangkan segmentasi berlebih dari mesh.

Pengenalan tipe permukaan

Tahap kedua adalah pengenalan permukaan. Setiap segmen harus didekati dengan permukaan dengan ketelitian yang ditentukan oleh sistem atau oleh pengguna.

Pertama, nilai-nilai kelengkungan utama dari segmen digunakan untuk menentukan apakah mungkin untuk menggambarkan bentuk segmen dengan salah satu permukaan dasar berikut:

• Pesawat: k ₁ = k ₂ = 0
• Sphere: k ₁ = k ₂ = K > 0
• Silinder: k ₁ = K > 0, k ₂ = 0
• Cone: k ₁ ∈ [ a , b ], k ₂ = 0
• Toroid: k ₁ = K , k ₂ ∈ [ a , b ]

Untuk membuat permukaan dasar, kita paskan objek geometris sederhana ke set titik menggunakan algoritma yang sesuai. Misalnya, agar sesuai dengan lingkaran dan bola ke satu set poin, metode kuadrat terkecil digunakan; agar sesuai dengan bidang, analisis komponen utama digunakan. Sistem ini memastikan bahwa setiap permukaan yang direkonstruksi terkait dengan segmen dalam ketepatan pengakuan yang telah ditentukan.

Gambar di bawah ini mengilustrasikan permukaan yang dikenali berdasarkan warna: bidang ditunjukkan dengan warna biru, silinder berwarna merah, bidang berwarna hijau, kerucut berwarna kuning, dan toroid violet.


Sumber mesh poligonal (kiri) dan mesh tersegmentasi (kanan) dengan segmen permukaan yang dikenal

Jika tidak ada permukaan dasar yang dapat menggambarkan segmen, maka sistem mencoba mengenali permukaan ekstrusi atau permukaan revolusi.

Ketika sistem pada akhirnya gagal menemukan permukaan analitis yang digunakan untuk menggambarkan bentuk segmen, permukaan NURBS dibuat untuk itu.

Pembuatan model B-rep

Tahap akhir dari transformasi adalah membuat model B-rep berdasarkan pada segmentasi dan data permukaan yang direkonstruksi. Grafik kedekatan dibuat dari daerah tersegmentasi untuk mewakili topologi model, dan membentuk dasar untuk membuat model B-rep yang dihasilkan. Model B-rep dirakit dalam mode otomatis penuh, berbeda dengan tahapan sebelumnya:

• Tepi B-rep dibuat dari kurva persimpangan dari permukaan yang direkonstruksi yang berdekatan
• Permukaan B-rep dikonstruksi oleh permukaan yang dikenali yang dibatasi dan tepi B-rep

Namun, tidak selalu memungkinkan untuk membuat shell dengan topologi yang benar. Misalnya, ambil dua permukaan seperti silinder dan bidang yang hampir bersinggungan satu sama lain di ruang angkasa. Karena toleransi yang ditentukan untuk permukaan yang direkonstruksi, mereka mungkin tidak berpotongan sama sekali. Akibatnya, shell yang dibuat mungkin memiliki cacat. Pengguna dapat menghilangkan cacat dengan memperbaiki parameter permukaan.

Jenis Model Poligon

Ada banyak sumber model poligonal yang tersedia online:

• Katalog dan basis data online menawarkan model 3D dalam format poligon seperti STL, VRML, dan OBJ dari 3D Warehouse, Cults 3D, dan sebagainya.
• File yang dihasilkan dari pemindaian 3D
• Output dari optimasi topologi model menggunakan algoritma CAE

Model-model poligonal dari sumber-sumber ini dapat dibagi menjadi dua kelompok: model-model yang triangulasi (disatukan) dari objek B-rep, dan semua model lainnya. Sepasang fitur khusus untuk kelompok pertama adalah tidak adanya kebisingan mesh poligonal dan dominasi permukaan analitis. Ini berarti bahwa model dari kelompok pertama dapat dengan mudah diubah menjadi b-repetisi dalam mode otomatis penuh atau dengan upaya pengguna yang minimal.

Jerat poligonal model dalam kelompok kedua memiliki kebisingan, mengandung permukaan organik, dan karenanya mereka cenderung membutuhkan partisipasi interaktif dari pengguna.

Jadi kami menyediakan dua mode untuk mengoperasikan C3D B-Shape, sepenuhnya otomatis dan interaktif. Pengguna dapat beralih di antara mode pengenalan, dan mengelola jenis permukaan selama proses rekonstruksi. Memilih mode dapat bergantung pada tujuan melakukan transformasi: pengguna kadang-kadang mungkin ingin mengabaikan konektivitas topologi dari shell yang dihasilkan, atau kebenaran keseluruhannya. Ini sering terjadi ketika mengoptimalkan tampilan dalam aplikasi BIM, di mana pengguna menambahkan elemen interior khusus ke model arsitektur.

Di sisi lain, tugas rekayasa balik memerlukan salinan yang paling akurat dari model sumber sehingga model yang dihasilkan memiliki topologi yang benar. Jadi, perlu untuk menentukan presisi, katakanlah, koaksialitas silinder atau singgung dua permukaan. Dalam kasus-kasus seperti ini, partisipasi pengguna dalam proses transformasi sangat penting.

Transformasi otomatis C3D B-Shaper menggunakan fungsi-fungsi berikut yang digunakan sebagai input data mesh pengaturan dan transformasi:

MbResultType ConvertMeshToShell( MbMesh & mesh, MbFaceShell *& shell, const MbMeshProcessorValues & params ); MbResultType ConvertCollectionToShell( MbCollection & collection, MbFaceShell *& shell, const MbMeshProcessorValues & params ); 

Salah satu pengaturan transformasi adalah nilai ketepatan pengakuan yang menetapkan toleransi maksimum untuk jarak antara simpul segmen dan permukaan yang dikenal. Ketepatannya bisa absolut atau relatif. Saat menggunakan presisi relatif, penyimpangan wajah dari badan mesh diukur relatif terhadap ukuran model.

Kelas antarmuka Prosesor MbMesh menawarkan opsi lanjutan untuk mengelola segmentasi dan pengenalan permukaan:

 class MbMeshProcessor { .. public: // Mesh rectification. void SetUseMeshSmoothing( bool useSmoothing ); // Mesh segmentation management. const MbCollection & GetSegmentedMesh(); MbResultType SegmentMesh( bool createSurfaces = true ); void ResetSegmentation(); void UniteSegments( size_t firstSegmentIdx, size_t secondSegmentIdx ); MbResultType SegmentMeshBySeparators( const std::vector<std::vector<uint>> & sep ); // Surface recognition management. void FitSurfaceToSegment( size_t idxSegment ); void FitSurfaceToSegment( size_t idxSegment, MbeSpaceType surfaceType ); const MbSurface * GetSegmentSurface( size_t idxSegment ) const; // B-rep shell construction. MbResultType CreateBRepShell( MbFaceShell *& pShell ); .. } 

Sebagai contoh, untuk mengoreksi hasil dari segmentasi otomatis, C3D B-Shaper menawarkan alat untuk menggabungkan dan membagi segmen, dan sebagainya. Pengguna dapat memasukkan permukaan jenis tertentu ke segmen yang dipilih, serta memodifikasi parameter permukaan yang dikenali.

Ringkasan

Hasil algoritma transformasi C3D B-Shaper diilustrasikan oleh gambar di bawah ini, di mana model 3D yang kompleks berhasil ditransformasikan dari representasi jala poligonal menjadi solid-representasi padatan.




Mesh poligonal (kiri) dan model B-rep (kanan) dikonversi dengan C3D B-Shaper

Tujuan kami adalah untuk membuat SDK yang kuat untuk mengubah model dari poligonal ke B-rep, dan pengembangan C3D B-Shaper terus berlanjut. Beberapa hal yang sedang kami kerjakan meliputi memajukan algoritma segmentasi otomatis, mengembangkan alat untuk mengedit segmentasi, meningkatkan konstruksi permukaan NURBS bentuk bebas, dan meningkatkan kualitas rakitan shell B-rep.

Pelanggan yang menggunakan kernel geometrik C3D juga merupakan faktor dalam mendorong pengembangan C3D B-Shaper.

Pengembang dipersilakan menguji C3D B-Shaper sebagai bagian dari C3D Toolkit atau sebagai komponen mandiri.

Oleh Andrey Tumanin, Pimpinan Pengembangan Perangkat Lunak di C3D Labs