Posit-arithmetic: mengalahkan floating point di bidangnya sendiri. Bagian 1

Bagian 2

Dari penerjemah: Topik format Posit sudah ada di hub di sini , tetapi tanpa detail teknis yang signifikan. Dalam publikasi ini, saya membawa kepada Anda terjemahan dari artikel oleh John Gustafson (penulis Posit) dan Isaac Yonemoto tentang format Posit.
Karena artikel itu memiliki volume yang besar, saya membaginya menjadi dua bagian. Daftar tautan ada di akhir bagian kedua.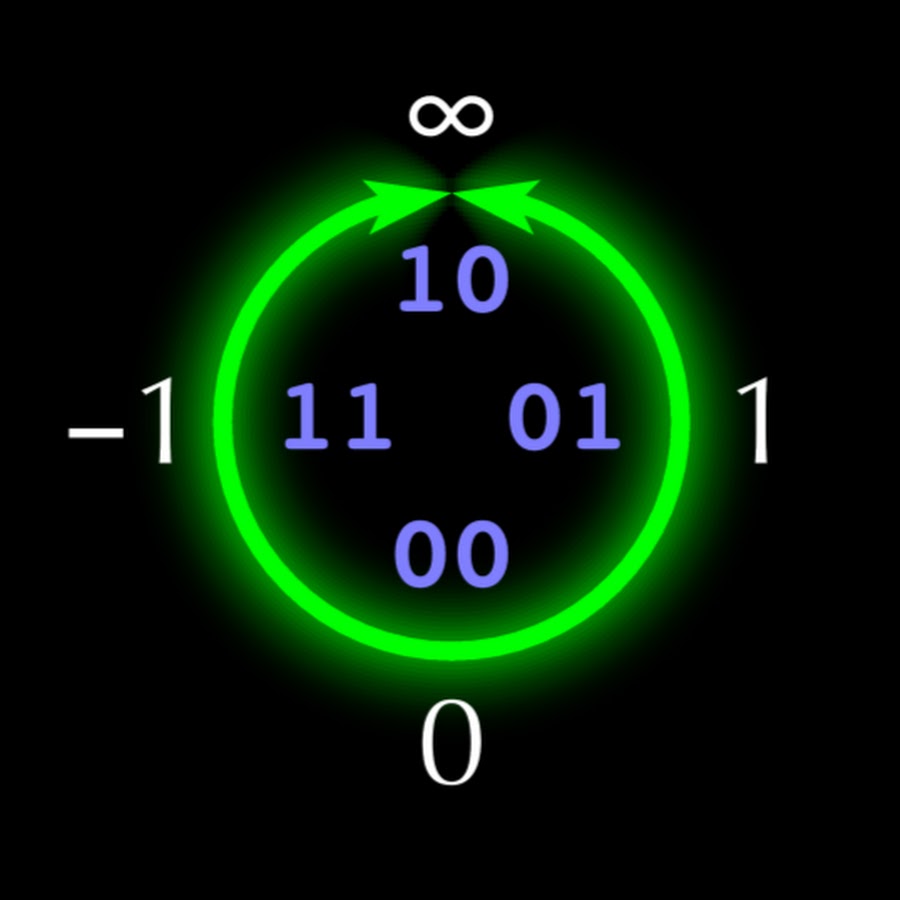



Tipe data baru, yang disebut posit, dirancang sebagai pengganti langsung untuk nomor floating point dari Standar IEEE 754. Berbeda dengan bentuk sebelumnya, unum aritmatika, standar posit tidak memerlukan penggunaan aritmatika interval atau operan berukuran variabel, dan, seperti float, nomor posit dibulatkan jika hasilnya tidak dapat direpresentasikan secara tepat. Mereka memiliki keunggulan yang tidak dapat disangkal atas format float, termasuk rentang dinamis yang lebih besar, akurasi yang lebih besar, kebetulan bitwise dari hasil perhitungan pada sistem yang berbeda, perangkat keras yang lebih sederhana dan dukungan yang lebih sederhana untuk pengecualian. Angka-angka posit tidak meluap baik hingga tak terbatas atau ke nol, dan "bukan angka" (Bukan angka, NaN) adalah tindakan, bukan kombinasi bit. Unit pengolah posit kurang kompleks daripada FPU IEEE. Ia mengkonsumsi lebih sedikit daya, dan lebih sedikit silikon, sehingga chip dapat melakukan lebih banyak operasi secara signifikan pada nomor posit per detik daripada FLOPS, dengan sumber daya perangkat keras yang sama. GPU dan prosesor pembelajaran dalam, khususnya, dapat melakukan lebih banyak operasi per watt konsumsi daya, yang akan meningkatkan kualitas pekerjaan mereka.

Tes komprehensif dilakukan membandingkan posisi dan float dalam hal akurasi perhitungan untuk berbagai akurasi posisi. Jumlah angka dengan presisi rendah adalah solusi terbaik untuk "perhitungan kasar" dalam kasus di mana akurasi rendah dapat diterima. Angka posisi presisi tinggi memberikan presisi lebih tinggi daripada pelampung dengan ukuran yang sama; dalam beberapa kasus, posisi 32-bit dapat dengan aman menggantikan pelampung 64-bit. Dengan kata lain, posit mengungguli float dalam gimnya sendiri.

Teori: Unums: Tipe I dan Tipe II

Kerangka aritmatika unum (angka universal, angka universal) memiliki beberapa bentuk untuk merepresentasikan angka. Bentuk aslinya adalah "Tipe I," sebuah superset dari IEEE 754; dia menggunakan ubit pada akhir bagian pecahan untuk menunjukkan bahwa bilangan real adalah tepat atau dalam kisaran antara bilangan real yang berdekatan. Terlepas dari kenyataan bahwa Unum, seperti float, memiliki tanda, bagian eksponen dan fraksional, panjang bagian eksponen dan fraksional bervariasi secara otomatis, dari satu bit ke nilai tertentu yang ditentukan oleh pengguna. Unum Tipe I adalah cara yang ringkas untuk merepresentasikan aritmatika interval tetapi panjang variabel membutuhkan usaha ekstra. Tipe ini dapat mengulangi perilaku float dengan menggunakan fungsi pembulatan khusus.

Bentuk angka universal “Tipe II” [4] tidak kompatibel dengan IEEE float, dan merupakan konsep yang bersih, matematis, keras berdasarkan pada bilangan real proyektif x. Gagasan utama di sini adalah bahwa bilangan bulat yang ditandatangani dalam kode add-on memetakan secara elegan ke bilangan real proyektif, dengan properti yang sama untuk beralih dari bilangan positif ke negatif, dan dengan urutan yang sama pada sumbu bilangan. Mengutip William Kahan [5]:
“Mereka menghemat ruang memori karena mereka tidak memanipulasi angka, tetapi menunjuk ke nilai. Dan ini memungkinkan untuk membuat aritmatika sangat, sangat cepat. "
Struktur unum 5-bit ditunjukkan pada Gambar. 1. Jika masing-masing unum memiliki n bit, maka "u-lattice" mengisi kuadran kanan atas lingkaran dengan seperangkat perintah $$$2 ^ {n-3} -1$ bilangan real $$$x_i$ (belum tentu rasional). Di kuadran kiri atas negatif $$$x_i$ tercermin relatif terhadap sumbu vertikal. Setengah bagian bawah lingkaran berisi angka-angka yang terbalik dengan angka - angka bagian atas, tercermin dari sumbu horizontal, yang membuat operasi perkalian dan pembagian sama simetrisnya seperti penjumlahan dan pengurangan. Seperti dengan Tipe I, nomor unum tipe II berakhir dengan 1 (ubit), mewakili interval terbuka antara titik-titik yang tepat berdekatan yang unum berakhir dengan 0 .


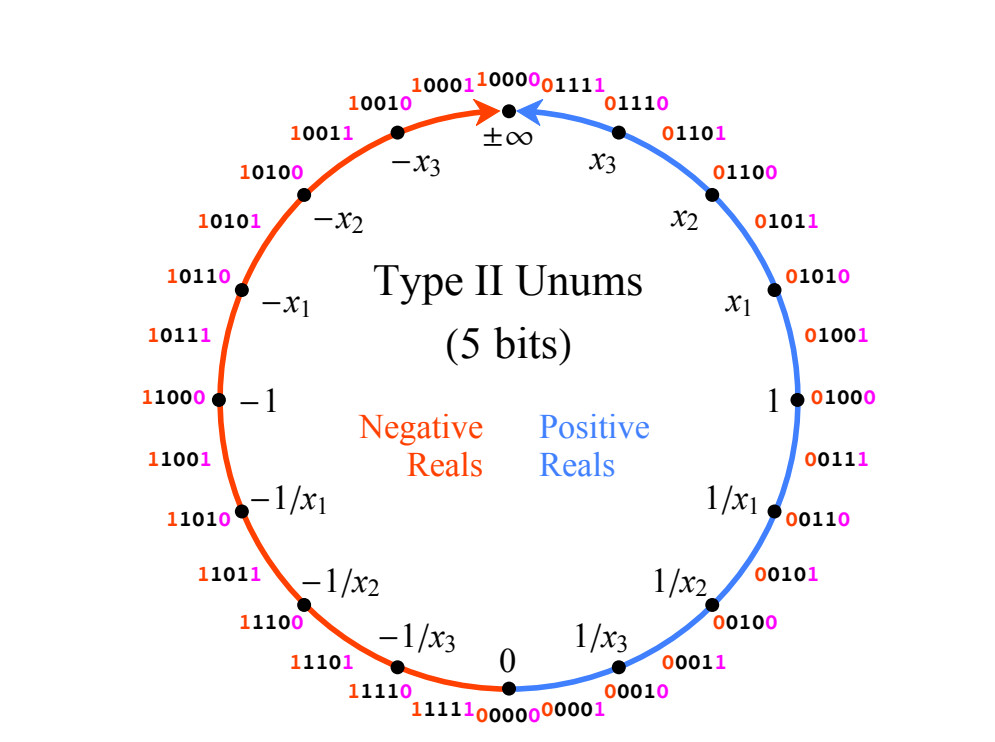Fig. 1. Garis bilangan real proyektif, dipetakan ke bilangan bulat dalam kode tambahan sepanjang 4 bit.

Angka unum tipe II memiliki banyak properti matematika yang ideal, tetapi sebagian besar operasi dengan mereka dilakukan menggunakan tabel pencarian . Jika n bit presisi diperlukan, maka tabel (dalam kasus terburuk) akan miliki $$$2 ^ {2n}$ nilai untuk fungsi dua argumen, tetapi dengan mempertimbangkan simetri akun dan trik lainnya, tabel dapat dikurangi menjadi ukuran yang lebih dapat diterima. Ukuran tabel membatasi skala format ultrafast ini hingga 20 bit atau kurang untuk teknologi saat ini. Tipe nomor unum tipe II juga tidak meminjamkan diri dengan baik untuk menggabungkan operasi. Kekurangan ini berfungsi sebagai motivasi untuk menemukan format yang mempertahankan banyak sifat nomor Unum Tipe II, tetapi lebih "ramah perangkat keras" dan dapat dihitung dengan sirkuit logika yang mirip dengan FPU yang ada.

2. Angka Posit dan Valid

Ada dua pendekatan yang berlawanan dengan perhitungan dalam bilangan real:

• Tidak ketat, tetapi murah, dan dapat diterima untuk sejumlah besar aplikasi praktis
• Matematis, bahkan dengan biaya waktu dan memori

Pernyataan pertama berkaitan dengan aritmatika nyata, di mana kesalahan pembulatan cukup kecil, pernyataan kedua berkaitan dengan aritmatika interval. Jumlah unum tipe I dan II juga dapat dipertimbangkan dalam nada yang sama, dan ini adalah salah satu alasan mengapa mereka adalah "bilangan universal." Namun, jika kita selalu akan menggunakan beberapa fungsi untuk pembulatan setelah setiap operasi, maka lebih baik kita tidak menggunakan bit terakhir sebagai bagian signifikan dari bagian pecahan dan bukan sebagai ubit. Angka unum dari jenis ini akan disebut nomor posit.

Kutipan dari New Oxford American Dictionary, edisi ke-3:

posit (kata benda): Sebuah pernyataan yang dibuat dengan asumsi bahwa itu ternyata benar.

Untuk menyederhanakan implementasi perangkat keras, nomor unum Tipe II melemahkan salah satu aturan: nilai invers yang tepat hanya ada untuk 0, $$$\ pm \ infty$ dan derajat dua. Ini memungkinkan kita untuk mengisi kisi-u sehingga bilangan akhir tetap sama dengan float, dan akan memiliki formulir $$$m \ cdot2 ^ k$ di mana k dan m adalah bilangan bulat. Tidak ada interval terbuka.

Valid adalah sepasang nomor posit dengan ukuran yang sama, masing-masing berakhir di ubit. Mereka dimaksudkan untuk digunakan dalam aplikasi-aplikasi tersebut di mana penting untuk secara ketat menentukan dalam interval berapa angka itu, misalnya, ketika men-debug algoritma numerik. Nilai-nilai yang valid lebih kuat daripada aritmatika interval biasa dan kurang rentan untuk dengan cepat memperluas batas interval yang terlalu pesimistis [2, 4]. Namun, mereka bukan subjek publikasi ini.

Gambar 2 menunjukkan struktur representasi posisi n-bit dengan bit eksponen.


Gambar 2. Format posit umum untuk mengikuti nilai bukan nol

Bit tanda mengandung 0 untuk angka positif, 1 untuk negatif. Untuk angka negatif, temukan Tambahan 2 sebelum mendekode mode, eksponen, dan bagian fraksional. Untuk memahami bit mode, pertimbangkan string biner yang ditunjukkan pada Tabel 1, di mana k berarti panjang urutan terdepan, dan x dalam bitstream berarti keadaan acuh tak acuh.

Tabel 1. Run-length artinya k dari bit rezim



Kami menyebut panjang urutan utama mode nomor. String biner dimulai dengan sejumlah nol atau satu dalam satu baris, diikuti oleh bit yang berlawanan, atau akhir dari string tercapai. Bit mode disorot dalam warna kuning, bit sebaliknya disorot dalam warna coklat. Misalkan m adalah jumlah bit identik dalam urutan, jika bit ini nol, maka k = -m, jika 1, maka k = m-1. Sebagian besar prosesor dapat menemukan unit pertama dalam sebuah kata atau nol pertama dalam sebuah kata dalam perangkat keras, yaitu, logika decoding sudah tersedia. Mode berarti faktor penskalaan sama dengan $$$useed ^ k$ dimana $$$useed = 2 ^ {2 ^ {es}}$ . Tabel 2 menunjukkan contoh nilai useed.

Tabel 2. digunakan sebagai fungsi es



Bit berikutnya (disorot dengan warna biru pada gambar) adalah eksponen e, yang merujuk ke bilangan bulat yang tidak ditandai. Itu tidak bergeser, seperti yang dilakukan di mengapung, itu merupakan penskalaan untuk $$$2 ^ e$ . Mungkin ada hingga bit eksponen, tergantung pada berapa banyak bit yang tersisa di sebelah kanan bit mode. Ini adalah cara ringkas untuk mengubah akurasi, angka yang mendekati 1 pada nilai absolut memiliki akurasi lebih besar daripada angka yang sangat besar atau sangat kecil, yang jauh lebih jarang terjadi dalam perhitungan.

Jika ada bit yang tersisa setelah mode dan bit eksponen, mereka mewakili bagian fraksional, f, sama seperti bagian fraksional 1.f dalam format float, tetapi bit tersembunyi selalu 1. Tidak ada angka denormalized dengan 0 tersembunyi, tidak seperti float.

Sistem yang kami jelaskan adalah konsekuensi alami dari pengisian u-grid. Mari kita mulai dengan posisi 3-bit sederhana, untuk kejelasan, dalam gambar. Gambar 3 menunjukkan hanya separuh kanan bilangan real proyektif. Jadi, angka dalam gambar. 3. Patuhi aturan Tipe II. Hanya ada dua nilai khusus: 0 (semua bit adalah 0) dan ± ∞ (unit diikuti oleh semua nol), urutan bitnya tidak mengikuti notasi posisi. Untuk nilai-nilai posit lain pada Gambar 3., bit-bitnya diberi warna seperti dijelaskan di atas. Perhatikan bahwa semua nilai positif pada Gambar 3 adalah nilai useed yang tepat dalam derajat k yang diwakili oleh bit mode.


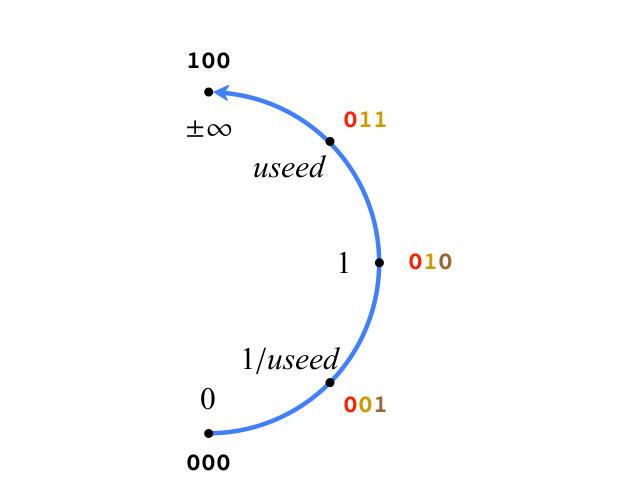Fig. 3. Nilai positif dari posisi 3-bit

Keakuratan angka Posit meningkat ketika bit ditambahkan, dan nilainya tetap di mana mereka berada di lingkaran ketika bit 0 ditambahkan. Ketika 1 ditambahkan, nilai baru dibuat antara dua nilai posit pada lingkaran. Nilai numerik apa yang harus kita berikan kepada mereka? Biarkan maxpos menjadi nilai positif terbesar dan minpos nilai positif terkecil pada lingkaran yang ditentukan oleh string bit. Dalam Gambar 3, maxpos adalah useed, dan minpos adalah 1 / useed. Aturan interpolasi adalah sebagai berikut:

Antara maxpos dan ± ∞, nilai baru adalah maxpos × useed; antara 0 dan minpos, nilai baru minpos / useed (dengan bit mode baru)
Antara Nilai Yang Ada $$$x = 2 ^ m$ dan $$$y = 2 ^ n$ , di mana m dan n berbeda lebih dari 1, nilai baru akan menjadi rata-rata geometriknya, $$$\ sqrt {x \ cdot y} = 2 ^ {(m + n) / 2}$ (dengan bit eksponen baru).
Dalam kasus lain, nilai baru terletak di tengah-tengah antara x dan y yang ada, yaitu, itu adalah rata-rata aritmatika, $$$(x + y) / 2$ (dengan bit fraksional baru)

Sebagai contoh, gbr. Gambar 4 memperlihatkan konstruksi angka posit dari 2 menjadi 5 bit dengan es = 2, dan dengan demikian menggunakan = 16.


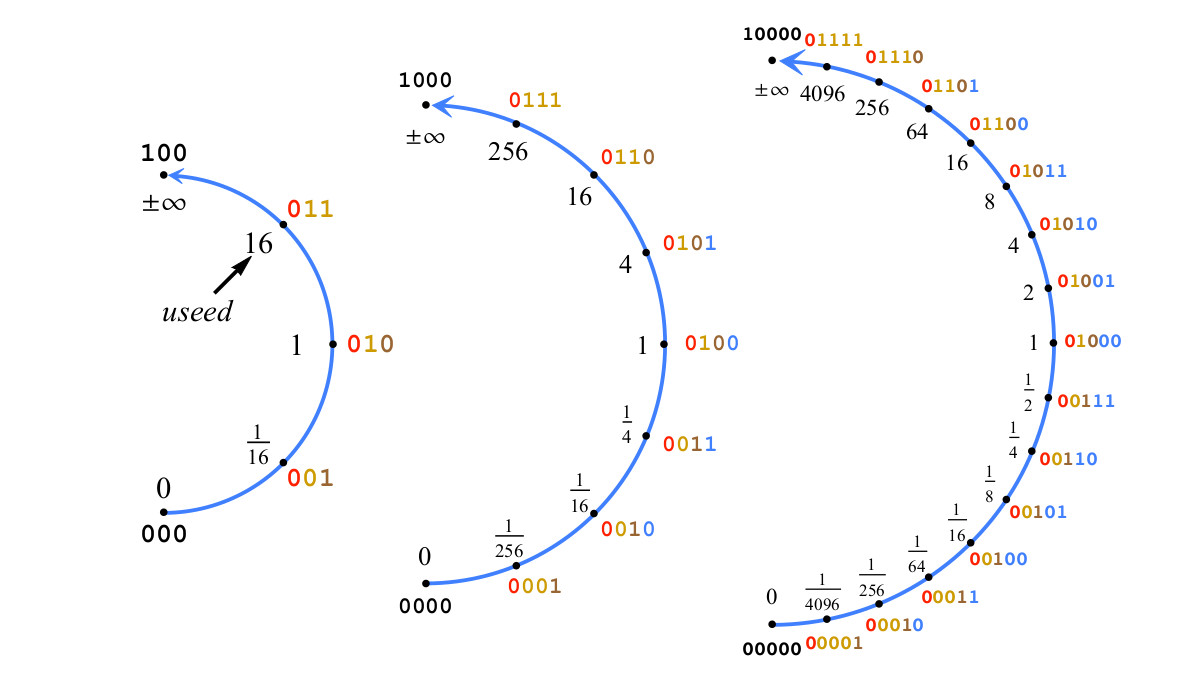Fig. 4. Membangun Posit dengan dua bit eksponen, $$$es = 2, useed = 2 ^ {2 ^ {es}} = $ 1$

Jika dalam gambar. 4 tambahkan satu bit lagi untuk mendapatkan posit 6-bit, ke angka posit yang mewakili rentang nilai antara 1/16 dan 16, bit bagian pecahan akan ditambahkan, bukan bit eksponen. Pertimbangkan string bit yang mewakili angka posit p sebagai bilangan bulat yang ditandatangani, mulai dari $$$-2 ^ {n-1}$ sebelumnya $$$2 ^ {n-1} -1$ . Biarkan k menjadi integer yang mewakili bit mode, e angka yang tidak ditandatangani mewakili bit eksponen, jika ada. Jika set bit adalah bagian fraksional $$$\ {f_1f_2 ... f_ {f_s} \}$ mungkin kosong lalu biarkan f menjadi nilai yang mewakili angka $$$1, f_1f_2 ... f_ {f_s}$ . Maka p mewakili

$$

$$x = \ begin {cases} 0, & p = 0, \\ \ pm \ infty, & p = -2 ^ {n-1}, tanda \\ (p) \ kali digunakan ^ k \ kali 2 ^ e \ times f \, & \ text {lainnya} p \ end {cases}$$

Mode dan es bit melakukan fungsi yang sama dengan bit eksponensial dalam float standar, bersama-sama mereka menentukan faktor penskalaan yang sama dengan kekuatan dua, dan setiap kenaikan menggunakan berarti pergeseran $$$2 ^ {es}$ sedikit. Jumlah maxpos adalah $$$useed ^ {n-2}$ dan minpos sama $$$useed ^ {2-n}$ . Contoh decoding nomor posit ditunjukkan pada Gambar. 5 (dengan nilai "non-standar" untuk es, untuk kesederhanaan).


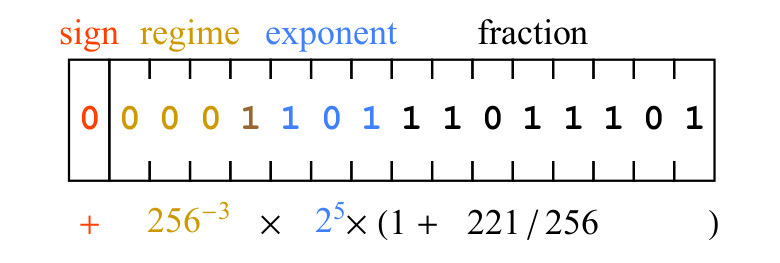Fig. 5. Contoh string bit posit dan makna matematikanya

Sedikit tanda 0 berarti nilainya positif. Bit mode 0001 memiliki urutan tiga nol, yang berarti bahwa k = -3, oleh karena itu, faktor penskalaan yang diperkenalkan oleh bit mode adalah $$$256 ^ {- 3}$ . Bit eksponen, 101, mewakili 5 sebagai bilangan bulat biner yang tidak ditandatangani, dan faktor penskalaan sisipan adalah $$$2 ^ 5$ . Akhirnya, bit dari bagian pecahan 11011101 mewakili angka 221, yaitu, bagian pecahan adalah 1 + 221/256. Ekspresi yang ditulis di bawah bitfield pada Gambar 5. menuntun kita pada hasilnya $$$477/134217728 \ approx3.55393 \ times10 ^ {- 6}$

2.2. Pelatihan jaringan saraf dan posisi 8-bit

Terlepas dari kenyataan bahwa standar IEEE tidak mendefinisikan float 8-bit, jumlah angka 8 bit dengan es = 0 telah membuktikan kegunaannya untuk beberapa tujuan, mereka sangat berguna untuk membangun jaringan saraf [3, 8]. Saat ini, nomor IEEE setengah presisi (16-bit) sering digunakan untuk tujuan ini, tetapi nomor posit 8-bit berpotensi diproses 2-4 kali lebih cepat. Fungsi penting dalam jaringan saraf adalah sigmoid, yang memiliki asimtot 0 untuk $$$x \ to- \ infty$ dan 1 untuk $$$x \ hingga \ infty$ . Pandangan umum tentang fungsi sigmoid $$$1 / (1 + e ^ {- x})$ , dan itu mahal untuk perhitungan, dan dapat dengan mudah memerlukan lebih dari seratus siklus prosesor untuk memanggil fungsi exp (x) dari perpustakaan, dan karena pembagian. Dengan angka posit, Anda bisa membalikkan bit pertama dari posit yang mewakili x, menggeser angka 2 bit ke kanan, mengisi bit di sebelah kiri dengan nol, dan fungsi posit yang dihasilkan, ditunjukkan pada Gambar 6. ungu, dekat dengan sigmoid (ditunjukkan dengan warna hijau), dan bahkan memiliki kemiringan yang sama saat melintasi sumbu y.


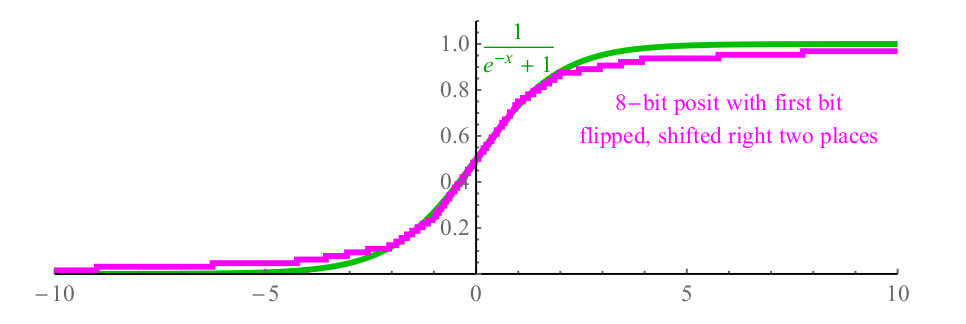Fig. 6. Fungsi sigmoid cepat menggunakan representasi posit

2.3. Diperlukan untuk mencapai dan melampaui rentang dinamis float

Kami mendefinisikan rentang dinamis sistem bilangan sebagai jumlah pesanan desimal dari yang terkecil ke nilai akhir positif terbesar, dari minpos ke maxpos. Artinya, rentang dinamis didefinisikan sebagai $$$log_ {10} (maxpos) −log_ {10} (minpos) = log_ {10} (maxpos / minpos)$ . Untuk posisi 8-bit dengan es = 0, minpos adalah 1/64 dan maxpos adalah 64, sehingga rentang dinamis adalah 3,6 desimal pesanan. Angka-angka posisi yang didefinisikan dengan es = 0 elegan dan sederhana, tetapi versi 16 dan 32-bit mereka memiliki rentang dinamis yang lebih kecil daripada pelampung IEEE dengan ukuran yang sama. Sebagai contoh, float IEEE 32-bit memiliki rentang dinamis 83 dekade, tetapi posisi 32-bit dengan es = 0 akan memiliki rentang dinamis hanya 18 dekade.

Di bawah ini adalah tabel nilai es yang memungkinkan angka posisi melebihi rentang dinamis float untuk ukuran 16-dan 32-bit, dan mendekati itu untuk ukuran 64-, 128- dan 256-bit.

Tabel 3. Rentang float dan posisi dinamis untuk jumlah bit yang sama



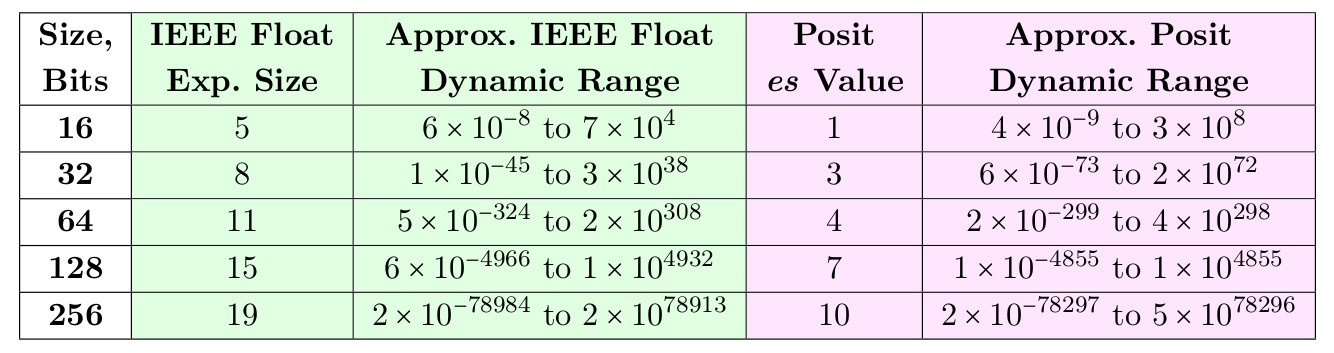
Salah satu alasan untuk memilih es = 3 untuk posit 32-bit adalah bahwa dalam hal ini mereka dapat berfungsi sebagai pengganti sederhana tidak hanya untuk float 32-bit, tetapi juga untuk 64-bit. Demikian pula, rentang dinamis 17 dekade untuk posisi 16-bit membuka jalan bagi mereka dalam aplikasi yang saat ini menggunakan pelampung 32-bit. Kami menunjukkan bahwa posit dapat mengungguli float dalam rentang dinamis dan akurasi pada ukuran bit yang sama.

2.4. Perbandingan kualitatif format Float dan Posit

Tidak ada "NaN" dalam format posit, sebagai gantinya, perhitungannya terputus, dan pengendali interupsi harus melaporkan kesalahan atau entah bagaimana memproses kesalahan dan melanjutkan perhitungan, tetapi angka posit tidak memungkinkan penetapan nilai tertentu yang menandakan kesalahan logis , yang, menurut definisi, adalah angka. Ini sangat menyederhanakan perangkat keras. Jika programmer melihat perlunya menggunakan nilai NaN, ini menunjukkan bahwa program belum selesai, dan angka yang valid harus digunakan dalam lingkungan debugging untuk menemukan dan menghilangkan kesalahan tersebut. Juga, posit tidak punya $$$+ \ infty$ dan $$$- \ infty$ , seperti float, angka yang valid mendukung interval terbuka $$$(maksimum, + \ infty)$ dan $$$(- \ infty, -maxpos)$ , yang memungkinkan untuk mewakili nilai tak terbatas dari tanda apa pun, dan kebutuhan untuk infinity yang ditandatangani hanya akan berarti bahwa alih-alih angka posit, Anda perlu menerapkan nilai yang valid.

Juga dalam tampilan posit tidak ada "nol negatif", nol negatif, ini adalah cacat logis lain yang ada dalam standar float IEEE. Dengan angka posit, jika a = b, maka f (a) = f (b). Standar IEEE 754 mengatakan bahwa angka terbalik ke -0 adalah $$$- \ infty$ , dan angka terbalik ke +0 adalah $$$+ \ infty$ , tetapi juga mengatakan bahwa -0 adalah +0. Karena itu, dipahami bahwa $$$- \ infty = + \ infty$ ?

Angka float memiliki algoritma perbandingan a = b yang canggih. Jika salah satu dari (a, b) adalah NaN, hasil perbandingan selalu negatif, bahkan jika representasi bit mereka sama. Jika representasi bit berbeda, maka masih ada kemungkinan bahwa a sama dengan b, karena nol negatif sama dengan nol positif! Dalam posix, pemeriksaan kesetaraan sama dengan untuk bilangan bulat: jika bit sama, angkanya sama. Jika ada bit yang berbeda, mereka tidak sama. Angka-angka posit memiliki hubungan yang sama (a <b) dengan bilangan bulat yang ditandatangani seperti dengan bilangan bulat yang ditandatangani, Anda harus memastikan bahwa tidak ada overflow dengan perubahan masuk, tetapi Anda tidak perlu instruksi mesin terpisah untuk membandingkan posit, jika Anda memiliki instruksi untuk membandingkan bilangan bulat yang ditandatangani.

Dalam format posit, tidak ada angka yang dinormalisasi, yaitu, tidak ada kombinasi bit khusus yang menunjukkan bahwa bit tersembunyi adalah 0 bukannya 1 . Posit tidak menggunakan anti-overflow, sebagai gantinya, penurunan akurasi secara bertahap digunakan, yang menyediakan fungsionalitas anti-overflow dan kasing simetrisnya, overflow (tidak seperti posit, float standar asimetris, dan menggunakan pola bit ini untuk mewakili sekumpulan nilai NaN yang besar dan tidak berguna).

Format float memiliki satu keunggulan dibandingkan posit, ketika mengembangkan perangkat keras, pengaturan tetap bit eksponen dan bagian fraksional memungkinkan mereka untuk diterjemahkan secara paralel.Dalam format posit, Anda harus mengikuti beberapa urutan, pertama decoding bit mode, dan kemudian bit yang tersisa. Ada cara sederhana untuk mengatasi batasan ini, mirip dengan trik yang digunakan untuk meningkatkan kecepatan penanganan pengecualian di float: beberapa bit tambahan melekat pada setiap nilai sehingga untuk menyimpan informasi ukuran di dalamnya ketika mendekode instruksi.

3. Kompatibilitas bitwise dan operasi gabungan

Salah satu alasan float IEEE tidak memberikan hasil yang identik pada sistem yang berbeda adalah karena untuk fungsi dasar, seperti $$$log(x)$ dan $$$cos(x)$IEEE tidak memerlukan ketelitian pada bit terakhir untuk setiap input yang memungkinkan. Lingkungan posisi harus benar menyelesaikan semua hasil operasi aritmatika yang didukung. (Beberapa pemrogram perpustakaan matematika khawatir tentang “dilema tabel dilema,” yaitu bahwa untuk beberapa nilai bisa sangat mahal untuk menentukan pembulatan yang benar, ini dapat dihilangkan dengan menggunakan tabel interpolasi alih-alih perkiraan polinomial.) Nilai yang tidak benar di bagian terakhir dari fungsi$$$e^x$, misalnya, pada akhirnya dapat menyebabkan sistem komputer memberi tahu kita bahwa 2 + 2 = 5.

Alasan yang lebih mendasar bahwa IEEE float tidak menghasilkan hasil duplikat pada sistem yang berbeda adalah bahwa standar memungkinkan penggunaan metode terselubung untuk menghindari overflow / anti-overflow, dan untuk meningkatkan akurasi operasi, seperti secara internal menyimpan bit carry tambahan untuk eksponensial dan fraksional. bagian. Aritmatika posisi melarang trik tersembunyi semacam itu.

Versi terbaru (2008) dari standar IEEE 754 [7] mencakup operasi penambahan-penggandaan gabungan dalam persyaratan. Ini adalah perubahan yang kontroversial, tidak disetujui oleh banyak anggota komite. Operasi gabungan menunda operasi pembulatan hingga operasi terakhir dalam perhitungan, yang mencakup lebih dari satu operasi, selesai setelah semua operasi, termasuk operasi integer yang tepat, selesai. Menggabungkan operasi tidak sama dengan operasi aritmatika presisi yang dapat diperluas, yang dapat meningkatkan panjang bilangan bulat hingga memori komputer menjadi penuh.

Lingkungan posit mensyaratkan adanya operasi gabungan berikut:

Gabungan-penambahan-perkalian$$$(a\times b)+c$
Gabungan Penambahan-Penggandaan $$$(a+b)\times c$
Penggandaan-Penggandaan-Penggandaan-Pengurangan $$$(a\times b)-(c\times d)$
Penjumlahan gabungan $$$\sum a_i$
Penggandaan skalar gabungan $$$\sum a_i b_i$

Perhatikan bahwa semua operasi dari daftar di atas adalah subset dari perkalian skalar gabungan [6] dalam hal persyaratan perangkat keras prosesor. Angka non-nol terkecil yang dapat diperoleh dengan menggunakan perkalian skalar adalah$$$minpos^2$ . Produk apa pun adalah bilangan bulat $$$minpos^2$ . Jika kita ingin mendapatkan produk skalar dari vektor $$$\{maxpos, minpos\}$ dan $$$\{maxpos, minpos\}$ sebagai operasi tepat di zona awal, kita perlu keseluruhan yang cukup besar untuk disimpan $$$maxpos^2/minpos^2$ . Ingat itu $$$maxpos=useed^{n-2}$ dan $$$minpos=1/maxpos$ . Dengan cara ini $$$maxpos^2/minpos^2=useed^{4n-8}$ .Dengan mempertimbangkan bit transfer dan pembulatan ke kekuatan dua, kami mendapatkan nilai yang direkomendasikan diberikan pada Tabel 4.

Tabel 4. Ukuran baterai yang tepat untuk setiap ukuran posisi



Dalam beberapa kasus, ukuran baterai sebanding dengan ukuran register, dalam kasus lain, diperlukan zona awal yang setara dengan cache L1 atau L2. Operasi gabungan dapat dilakukan perangkat lunak atau perangkat keras, tetapi harus tersedia untuk dieksekusi dalam lingkungan posit.