🤚🏿 👒 🕯️ Regresi linier dan metode untuk pemulihannya ✝️ 🕠 🏂🏽

Sumber: xkcd

Regresi linier adalah salah satu algoritma dasar untuk banyak bidang yang terkait dengan analisis data. Alasannya jelas. Ini adalah algoritma yang sangat sederhana dan dapat dipahami, yang telah berkontribusi pada penggunaannya yang luas selama puluhan, bahkan ratusan, tahun. Idenya adalah bahwa kita mengasumsikan ketergantungan linear dari satu variabel pada satu set variabel lain, dan kemudian mencoba untuk mengembalikan ketergantungan ini.

Tetapi artikel ini bukan tentang menerapkan regresi linier untuk menyelesaikan masalah praktis. Di sini kita akan membahas fitur menarik dari penerapan algoritma terdistribusi untuk pemulihannya yang kami temui saat menulis modul pembelajaran mesin di Apache Ignite . Sedikit matematika dasar, dasar-dasar pembelajaran mesin, dan komputasi terdistribusi akan membantu Anda mengetahui cara mengembalikan regresi linier, bahkan jika data didistribusikan di ribuan node.

Apa yang kamu bicarakan

Kita dihadapkan dengan tugas memulihkan ketergantungan linear. Sebagai masukan, banyak vektor dari variabel yang dianggap independen diberikan, yang masing-masing dikaitkan dengan nilai tertentu dari variabel dependen. Data-data ini dapat direpresentasikan dalam bentuk dua matriks:

\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}

$\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$

Sekarang, karena ketergantungan diasumsikan, dan selain itu linier, kami menuliskan asumsi kami dalam bentuk produk matriks (untuk menyederhanakan notasi di sini dan di bawah, diasumsikan bahwa istilah bebas persamaan tersembunyi di balik

x_{n}

$x_n$ , dan kolom terakhir dari matriks

A

$A$ berisi unit):

\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ kali \ mulai {pmatrix} x_ { 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \ end {pmatrix} = \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}

$\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ kali \ mulai {pmatrix} x_ { 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \ end {pmatrix} = \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$

Sangat mirip dengan sistem persamaan linear, bukan? Tampaknya, tetapi kemungkinan besar tidak akan ada solusi untuk sistem persamaan seperti itu. Alasan untuk ini adalah kebisingan yang ada di hampir semua data nyata. Selain itu, alasannya mungkin karena kurangnya hubungan linear, yang dapat Anda coba perjuangkan dengan memperkenalkan variabel tambahan yang secara nonlinier bergantung pada sumbernya. Perhatikan contoh berikut:
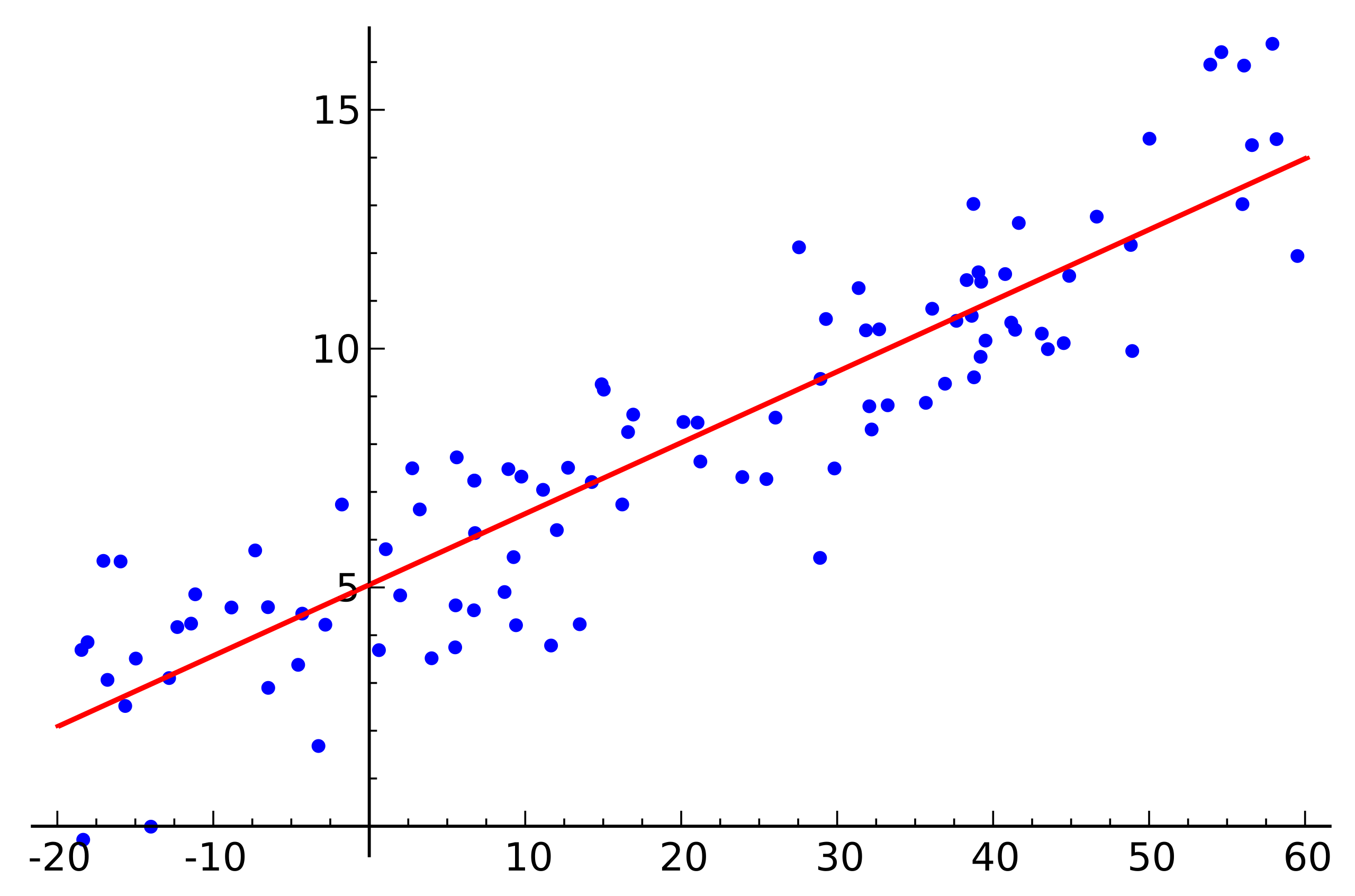gambar

Sumber: Wikipedia

Ini adalah contoh regresi linier sederhana yang menunjukkan ketergantungan satu variabel (di sepanjang sumbu

y

$y$ ) dari variabel lain (sepanjang sumbu

x

$x$ ) Agar sistem persamaan linear yang sesuai dengan contoh ini memiliki solusi, semua titik harus terletak tepat pada satu garis lurus. Tapi ini tidak benar. Tetapi mereka tidak terletak pada satu garis lurus justru karena kebisingan (atau karena asumsi adanya ketergantungan linier adalah keliru). Jadi, untuk mengembalikan ketergantungan linier dari data nyata, biasanya perlu untuk memperkenalkan satu asumsi lagi: data input mengandung noise dan noise ini memiliki distribusi normal . Seseorang dapat membuat asumsi tentang jenis-jenis lain dari distribusi kebisingan, tetapi dalam sebagian besar kasus itu adalah distribusi normal yang akan dibahas nanti.

Metode kemungkinan maksimum

Jadi, kami mengasumsikan adanya noise acak yang terdistribusi normal. Bagaimana bisa berada dalam situasi seperti itu? Untuk kasus ini, dalam matematika ada dan banyak digunakan metode kemungkinan maksimum . Singkatnya, esensinya terletak pada pilihan fungsi kemungkinan dan maksimalisasi selanjutnya.

Kami kembali ke pemulihan ketergantungan linier dari data dengan noise normal. Perhatikan bahwa hubungan linear yang diasumsikan adalah ekspektasi matematis

m u

$\ mu$ distribusi normal tersedia. Pada saat yang sama, probabilitas itu

m u

$\ mu$ mengasumsikan satu atau nilai lain, tergantung pada kehadiran yang dapat diamati

x

$x$ , terlihat sebagai berikut:

P (m u m i d X, s i g m a^{2}) = p r o d_{x i n X} f r a c 1 s i g m a s q r t 2 p i e^{- f r a c (x - m u)^{2} 2 s i g m a^{2}}

$P (\ mu \ mid X, \ sigma ^ 2) = \ prod_ {x \ in X} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}}$

Kami mengganti sekarang

m u

$\ mu$ dan

X

$X$ variabel yang kita butuhkan:

P (x m i d A, B, s i g m a^{2}) = p r o d_{i i n [1, m]} f r a c 1 s i g m a s q r t 2 p i e^{- f r a c (b_{i} - a_{i} x)^{2} 2 s i g m a^{2}}, a_{i} d i A, b_{i} d a l a m B

$P (x \ mid A, B, \ sigma ^ 2) = \ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}}}, a_i \ di A, b_i \ dalam B$

Tetap hanya untuk menemukan vektor

x

$x$ di mana probabilitas ini maksimum. Untuk memaksimalkan fungsi seperti itu, lebih mudah untuk prologaritma pertama (logaritma fungsi akan mencapai maksimum pada titik yang sama dengan fungsi itu sendiri):

f (x) = l n (p r o d_{i i n [1, m]} f r a c 1 s i g m a s q r t 2 p i e^{- f r a c (b_{i} - a_{i} x)^{2} 2 s i g m a^{2}}) = s u m_{i i n [1, m]} l n f r a c 1 s i g m a s q r t 2 p i - s u m_{i i n [1, m]} f r a c (b_{i} - a_{i} x)^{2} 2 s i g m a^{2}

$f (x) = ln (\ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix ) ^ 2} {2 \ sigma ^ 2}}}) = \ sum_ {i \ in [1, m]} ln \ frac {1} {\ sigma \ sqrt {2 \ pi}} \; - \ sum_ {i \ in [1, m]} \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}$

Yang, pada gilirannya, bermuara untuk meminimalkan fungsi berikut:

f (x) = s u m_{i i n [1, m]} (b_{i} - a_{i} x)^{2}

$f (x) = \ sum_ {i \ in [1, m]} (b_i-a_ix) ^ 2$

Omong-omong, ini disebut metode kuadrat terkecil . Seringkali, semua alasan di atas dihilangkan dan metode ini hanya digunakan.

Dekomposisi QR

Minimum fungsi di atas dapat ditemukan jika Anda menemukan titik di mana gradien fungsi ini sama dengan nol. Dan gradien akan ditulis sebagai berikut:

n a b l a f (x) = s u m_{i d a l a m [1, m]} 2 a_{i} (a_{i} x - b_{i}) = 0

$\ nabla f (x) = \ sum_ {i \ dalam [1, m]} 2a_i (a_ix - b_i) = 0$

Dekomposisi QR adalah metode matriks untuk memecahkan masalah minimisasi yang digunakan dalam metode kuadrat terkecil. Dalam hal ini, kami menulis ulang persamaan dalam bentuk matriks:

A^{T} A x = A^{T} b

$A ^ T A x = A ^ Tb$

Jadi, kami paparkan matriksnya

A

$A$ pada matriks

Q

$Q$ dan

R

$R$ dan melakukan serangkaian transformasi (algoritma dekomposisi QR itu sendiri tidak akan dipertimbangkan di sini, hanya penggunaannya dalam kaitannya dengan tugas):

\ begin {align} & (QR) ^ T (QR) x = (QR) ^ Tb; \\ & R ^ T Q ^ T Q R x = R ^ T Q ^ T b; \\ \ end {align}

$\ begin {align} & (QR) ^ T (QR) x = (QR) ^ Tb; \\ & R ^ T Q ^ T Q R x = R ^ T Q ^ T b; \\ \ end {align}$

Matriks

Q

$Q$ bersifat ortogonal. Ini memungkinkan kita untuk menyingkirkan pekerjaan.

Q Q^{T}

$Q Q ^ T$ :

\ begin {align} & R ^ T R x = R ^ T Q ^ T b; \\ & (R ^ T) ^ {- 1} R ^ T R x = (R ^ T) ^ {- 1} R ^ T Q ^ T b; \\ & R x = Q ^ T b. \ end {align}

$\ begin {align} & R ^ T R x = R ^ T Q ^ T b; \\ & (R ^ T) ^ {- 1} R ^ T R x = (R ^ T) ^ {- 1} R ^ T Q ^ T b; \\ & R x = Q ^ T b. \ end {align}$

Dan jika Anda ganti

Q^{T} b

$Q ^ T b$ pada

z

$z$ itu akan berubah

R x = z

$R x = z$ . Mengingat itu

R

$R$ adalah matriks segitiga atas, terlihat seperti ini:

\ begin {pmatrix} r_ {11} & r_ {12} & r_ {13} & r_ {14} & ... & r_ {1n} \\ 0 & r_ {22} & r_ {23} & r_ { 24} & ... & r_ {2n} \\ 0 & 0 & r_ {33} & r_ {34} & ... & r_ {3n} \\ 0 & 0 & 0 & 0 & 0 & r_ {44} & .. . & r_ {4n} \\ ... \\ 0 & 0 & 0 & 0 & ... & r_ {nn} \\ \ end {pmatrix} \ kali \ mulai {pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \ begin {pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ end {pmatrix}

$\ begin {pmatrix} r_ {11} & r_ {12} & r_ {13} & r_ {14} & ... & r_ {1n} \\ 0 & r_ {22} & r_ {23} & r_ { 24} & ... & r_ {2n} \\ 0 & 0 & r_ {33} & r_ {34} & ... & r_ {3n} \\ 0 & 0 & 0 & 0 & 0 & r_ {44} & .. . & r_ {4n} \\ ... \\ 0 & 0 & 0 & 0 & ... & r_ {nn} \\ \ end {pmatrix} \ kali \ mulai {pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \ begin {pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ end {pmatrix}$

Ini dapat diselesaikan dengan metode substitusi. Barang

x_{n}

$x_n$ seperti

z_{n} / r_{n n}

$z_n / r_ {nn}$ item sebelumnya

x_{n - 1}

$x_ {n-1}$ seperti

(z_{n - 1} - r_{n - 1, n} x_{n}) / r_{n - 1, n - 1}

$(z_ {n-1} - r_ {n-1, n} x_n) / r_ {n-1, n-1}$ dan sebagainya.

Perlu dicatat di sini bahwa kompleksitas algoritma yang dihasilkan melalui penggunaan dekomposisi QR adalah

O (2 j u t a^{2})

$O (2juta ^ 2)$ . Selain itu, meskipun fakta bahwa operasi perkalian matriks diparalelkan dengan baik, tidak mungkin untuk menulis versi terdistribusi yang efektif dari algoritma ini.

Keturunan gradien

Berbicara tentang meminimalkan fungsi tertentu, selalu layak untuk mengingat metode penurunan gradien (stokastik). Ini adalah metode minimisasi yang sederhana dan efektif berdasarkan iteratif menghitung gradien fungsi pada suatu titik dan kemudian menggesernya ke sisi yang berlawanan dengan gradien. Setiap langkah tersebut membuat solusi menjadi minimum. Gradien terlihat sama:

n a b l a f (x) = s u m_{i d a l a m [1, m]} 2 a_{i} (a_{i} x - b_{i})

$\ nabla f (x) = \ sum_ {i \ dalam [1, m]} 2a_i (a_ix - b_i)$

Metode ini juga paralel dan terdistribusi dengan baik karena sifat linier dari operator gradien. Perhatikan bahwa dalam rumus di atas, istilah independen berada di bawah tanda penjumlahan. Dengan kata lain, kita dapat menghitung gradien secara independen untuk semua indeks

i

$i$ dari pertama hingga

k

$k$ , bersamaan dengan ini, hitung gradien untuk indeks dengan

k + 1

$k + 1$ sebelumnya

m

$m$ . Kemudian tambahkan gradien yang dihasilkan. Hasil dari penambahan akan sama seperti jika kita segera menghitung gradien untuk indeks dari yang pertama sampai

m

$m$ . Dengan demikian, jika data didistribusikan antara beberapa bagian data, gradien dapat dihitung secara independen pada setiap bagian, dan kemudian hasil perhitungan ini dapat dijumlahkan untuk mendapatkan hasil akhir:

n a b l a f (x) = s u m_{i d i P_{1}} 2 a_{i} (a_{i} x - b_{i}) + s u m_{i d a l a m P_{2}} 2 a_{i} (a_{i} x - b_{i}) + . . . + s u m_{i d i P_{k}} 2 a_{i} (a_{i} x - b_{i})

$\ nabla f (x) = \ sum_ {i \ di P_1} 2a_i (a_ix - b_i) + \ sum_ {i \ dalam P_2} 2a_i (a_ix - b_i) + ... + \ sum_ {i \ di P_k} 2a_i (a_ix - b_i)$

Dalam hal implementasi, ini cocok dengan paradigma MapReduce . Pada setiap langkah penurunan gradien, tugas untuk menghitung gradien dikirim ke setiap node data, kemudian gradien yang dihitung dikumpulkan bersama-sama, dan hasil penjumlahannya digunakan untuk meningkatkan hasilnya.

Terlepas dari kesederhanaan implementasi dan kemampuan untuk mengeksekusi dalam paradigma MapReduce, gradient descent juga memiliki kekurangannya. Secara khusus, jumlah langkah yang diperlukan untuk mencapai konvergensi jauh lebih besar dibandingkan dengan metode lain yang lebih khusus.

LSQR

LSQR adalah metode lain untuk memecahkan masalah, yang cocok untuk merekonstruksi regresi linier dan untuk memecahkan sistem persamaan linear. Fitur utamanya adalah menggabungkan keunggulan metode matriks dan pendekatan berulang. Implementasi metode ini dapat ditemukan baik di perpustakaan SciPy dan di MATLAB . Deskripsi metode ini tidak akan diberikan di sini (dapat ditemukan di artikel LSQR: Algoritma untuk persamaan linear jarang dan kuadrat terkecil jarang ). Sebagai gantinya, suatu pendekatan akan didemonstrasikan untuk menyesuaikan LSQR dengan eksekusi di lingkungan terdistribusi.

Metode LSQR didasarkan pada prosedur bidiagonisasi. Ini adalah prosedur berulang, setiap iterasi terdiri dari langkah-langkah berikut:
gambar

Tetapi berdasarkan fakta bahwa matriks

A

$A$ dipartisi secara horizontal, maka setiap iterasi dapat direpresentasikan sebagai dua langkah MapReduce. Dengan demikian, dimungkinkan untuk meminimalkan transfer data selama setiap iterasi (hanya vektor dengan panjang yang sama dengan jumlah yang tidak diketahui):

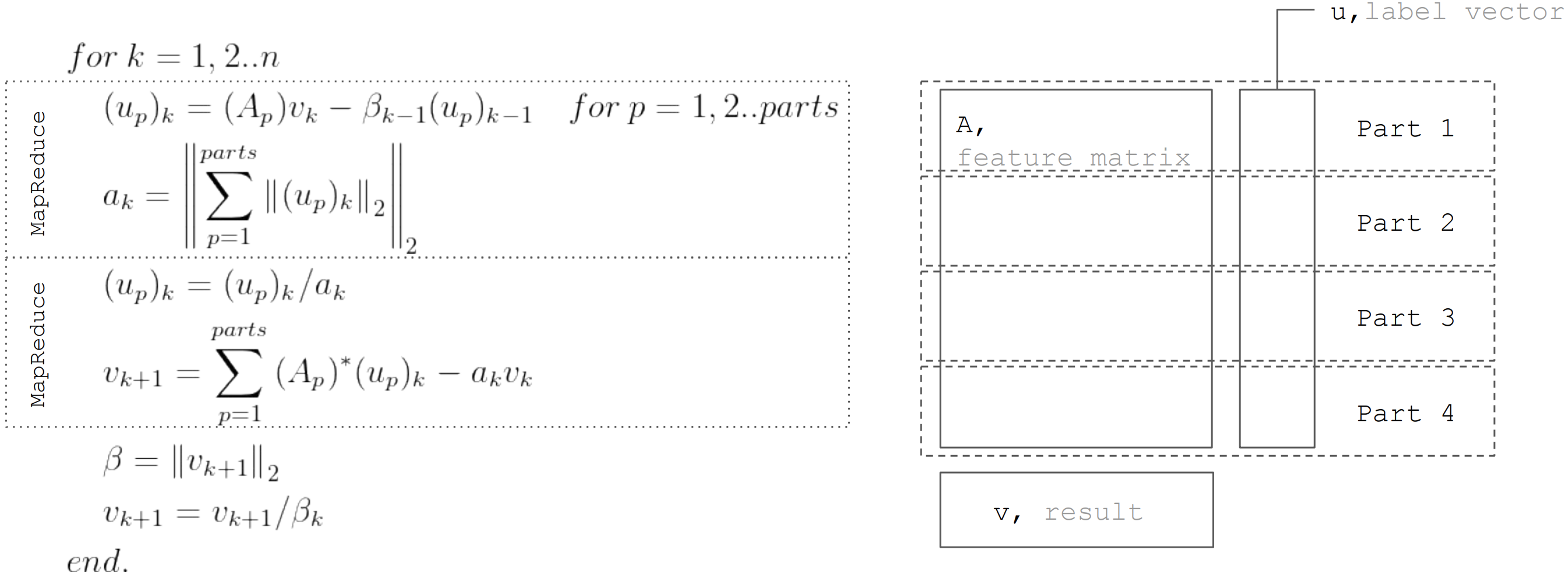
gambar

Pendekatan ini digunakan ketika menerapkan regresi linier di Apache Ignite ML .

Kesimpulan

Ada banyak algoritma pemulihan regresi linier, tetapi tidak semuanya dapat diterapkan dalam kondisi apa pun. Jadi dekomposisi QR sangat bagus untuk solusi akurat pada array data kecil. Gradient descent hanya diimplementasikan dan memungkinkan Anda untuk dengan cepat menemukan solusi perkiraan. Dan LSQR menggabungkan sifat-sifat terbaik dari dua algoritma sebelumnya, karena dapat didistribusikan, konvergen lebih cepat dibandingkan dengan gradient descent, dan juga memungkinkan penghentian awal algoritma, tidak seperti dekomposisi QR, untuk menemukan solusi perkiraan.