Di Habré sudah ada banyak artikel yang ditujukan untuk perhitungan cepat trigonometri ketika itu sangat diperlukan, tetapi saya ingin menambah mereka dengan satu catatan kecil dengan referensi ke trigonometri sekolah.
Terkadang mungkin tidak ada implementasi perangkat keras trigonometri, kadang-kadang ada alasan lain untuk menemukan metode untuk mempercepat perhitungan.
Matematika
Mari kita ingat beberapa rumus sederhana dari kursus sekolah.
Mari kita mulai dengan yang sederhana:
(1)
sin x = cos (90° - x)cos x = sin (90° - x)sin -x = -sin xcos -x = cos x- Dalam kasus umum,
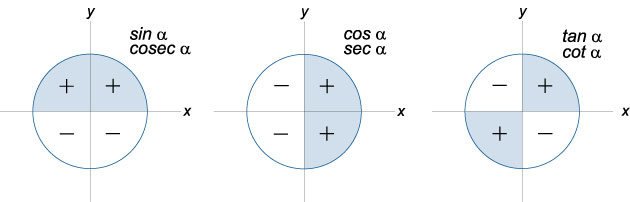
sin (90°N ± x) = ±cos x untuk N aneh dan ±sin x untuk genap. Tanda diambil berdasarkan tanda argumen di kuartal yang sesuai dari lingkaran.
Selanjutnya:
(2)
cos (x + y) = cos x cos y - sin x sin ysin (x + y) = sin x cos y + cos x sin y
Dan juga:
(3)
sin x = x - x^3/3! + x^5/5! - ...cos x = 1 - x^2/2! + x^4/4! - ...
Kosinus / sinus dari sudut mana pun dapat direduksi menjadi argumen dalam rentang dari 0 ° hingga 45 ° menggunakan rumus dari kelompok pertama.
Untuk sudut kecil, fungsi trigonometrik dapat direduksi menjadi ekspansi asimptotik jika istilah yang dibuang sengaja melampaui kisi debit.
Semua sudut menengah dapat diperoleh dengan menjumlahkan sudut besar dengan langkah tertentu (dan bagi mereka trigonometri dapat dianggap tabular), dan residu yang cepat atau lambat akan memberikan dekomposisi linier.
Aplikasi
Misalkan kita bekerja dengan nomor presisi tunggal IEEE-754, mereka memiliki nama float, single, dll. Ada 23 karakter dalam mantissa, yang berarti kita perlu mendapatkan kesalahan relatif 2^-23 .
Mari kita evaluasi seberapa dalam Anda perlu turun untuk membangun tabel argumen.
Untuk sinus, kita membuang istilah kubik, jadi kita perlu hubungannya dengan yang linear lebih kecil dari kesalahan yang diizinkan, yang berarti: 1 - (x - x^3/3!) / x = x^2/6 2/6 2 ^ -23, maka dari itu untuk argumen yang tidak lebih dari 0,000846 radian, keakuratan perhitungan perkiraan untuk sinus sudah cukup untuk kita. Untuk cosinus, jika Anda menjatuhkan istilah kuadratik, Anda memerlukan akurasi sekitar 2 kali lebih baik - 0,000488 radian.
Jadi, kita tidak perlu memiliki nilai tabular untuk argumen yang kurang dari 0,000488 radian.
Untuk membangun tabel, kita renormalisasi argumen input sehingga nilai 0 sesuai dengan sudut 0 °, dan untuk nilai 1 sesuai dengan sudut 45 °, atau pi/4=0.78539816 radian. Maka sudut minimum yang diperoleh di atas akan dikonversi menjadi 0,0006217 radian, atau sekitar 1/1600 - ini lebih dari 1/2048 = 2^-11 .
Selanjutnya, Anda harus memilih langkah dari tabel berdasarkan bagaimana kami ingin mendistribusikan perhitungan, kami akan membagi eksponen 11 menjadi beberapa bagian. Misalnya, Anda dapat membaginya menjadi dua bagian: 11 = 6 + 5, maka kita membutuhkan dua tabel ukuran 64 dan 32 catatan (total 96), atau tiga bagian: 11 = 4 + 4 + 3 (ukuran tabel 16 + 16 + 8 = 40 entri), tetapi akan ada lebih banyak operasi perkalian - pilihan spesifik akan tergantung pada tugas dan sumber daya yang tersedia.
Catatan: entri tabel adalah sepasang argumen sinus dan kosinus. Jika disimpan dengan presisi tunggal, maka ukuran rekaman adalah 8 byte.
Contoh
Mari kita ambil dekomposisi 4 + 4 + 3 sebagai contoh, dan kemudian menggeneralisasi.
Jadi, tugasnya: menghitung nilai sin x untuk x sewenang-wenang.
Langkah 1. Kami membawa argumen x ke skala kami, membaginya dengan pi/4 konstan pi/4 (sebut saja x' ).
Langkah 2. Bergantung pada nilai argumen x' menggunakan rumus (1), kami memilih fungsi yang diinginkan sehingga argumennya berada dalam rentang dari 0 hingga 1 (inklusif) (sebut saja x'' . Pada langkah ini, Anda juga harus menandai tanda hasil .
[misalkan misalnya bahwa sinus adalah]
Langkah 3. Kami akan menggunakan tabel (saya akan mengingatkan Anda bahwa ada 3 di antaranya), sedangkan indeks dalam tabel akan menjadi "bidang bit" dalam representasi biner dari argumen x'' - 4 bit pertama setelah titik desimal, kemudian 4 lagi, dan 3 lagi, dan sisanya untuk bisnis bit akan pergi ke sisanya.
Tabel sinus disebut S1, S2, S3, tabel cosinus adalah C1, C2, C3.
Karena kita membagi sudut dengan pi/4 , untuk mendapatkan sisanya dalam radian, itu harus dikalikan dengan jumlah yang sama. Sisa "bit" dikalikan dengan pi/4 dilambangkan dengan A. Kemudian sinusnya akan sama dengan A, dan cosinus - 1.
Langkah 4. Gabungkan semua yang terjadi:
C12 = C1 C2 - S1 S2 S12 = S1 C2 + C1 S2 C123 = C12 C3 - S12 S2 S123 = S12 C3 + C12 S3
|sin x| = S123 + C123 A |sin x| = S123 + C123 A (jika Anda mendapatkan sinus di langkah 2)
|sin x| = C123 - S123 A |sin x| = C123 - S123 A (jika Anda menerima kosinus pada langkah 2)
Langkah 5. Jika pada langkah 2 kami menganggap bahwa hasilnya harus negatif, maka minus ini harus dimasukkan ke dalam hasil.
Kesimpulan
Pendekatan serupa dapat digunakan baik untuk menghitung dalam bilangan real dari berbagai ukuran, dan, misalnya, untuk menerapkan aritmatika titik tetap khusus. Sebenarnya, pada suatu waktu itu hanya tugas terakhir yang membuat saya menggali lebih dalam ke arah ini, tapi itu sudah lama sekali.