Pertumbuhan. Berat Tiga tetangga

Dalam mencari DataSet yang menarik dan sederhana, saya menemukan pria tampan ini .

Tentang keindahan ini

Ini berisi data tentang pertumbuhan dan berat 10.000 pria dan wanita . Tidak ada deskripsi. Tidak ada yang "berlebihan." Hanya tinggi, berat dan tanda lantai. Saya menyukai kesederhanaan misterius ini.

Baiklah, mari kita mulai!

Apa yang menarik bagi saya?

• Berapa kisaran berat dan tinggi badan untuk kebanyakan pria dan wanita?
• Pria "rata-rata" seperti apa dan wanita "rata-rata" itu?
• Dapatkah model pembelajaran mesin KNN sederhana dari data ini memprediksi berat dengan tinggi ?

Ayo pergi!

Penampilan pertama

Pertama, muat modul yang diperlukan

#      import pandas as pd #     import matplotlib.pyplot as plt %matplotlib inline #    «  » from sklearn.neighbors import KNeighborsRegressor #         from sklearn.model_selection import train_test_split 

Ketika perpustakaan berdiri persis - sudah waktunya untuk memuat DataSet itu sendiri dan melihat 10 elemen pertama. Ini diperlukan agar usus kita tenang, bahwa kita telah memuat semuanya dengan benar.

Ngomong-ngomong, jangan khawatir bahwa tinggi dan berat badan berbeda dari yang biasa kita alami. Ini karena sistem pengukuran yang berbeda: inci dan pound , bukan sentimeter dan kilogram .

 data = pd.read_csv('weight-height.csv') data.head(10) 

Bagus! Kita melihat bahwa sepuluh entri pertama adalah "laki-laki". Kami melihat tinggi dan berat badan mereka . Data dimuat dengan baik.

Sekarang Anda dapat melihat jumlah baris di set.

 data.shape >> (10000, 3) 

Sepuluh ribu baris / catatan. Dan masing-masing memiliki tiga parameter . Apa yang kamu butuhkan!

Sudah waktunya untuk memperbaiki sistem pengukuran. Sekarang ada beberapa sentimeter dan kilogram.

 data['Height'] *= 2.54 data['Weight'] /= 2.205 #    data.head(10) 

Sekarang telah menjadi lebih akrab. Dan catatan pertama memberi tahu kita tentang seorang pria dengan tinggi ~ 190cm dan berat ~ 110kg. Pria besar Sebut saja dia Bob.

Tetapi bagaimana memahami: apakah banyak atau sedikit dibandingkan dengan yang lain? Apakah mungkin kita semua Kacang plus atau minus? Ini sedikit kemudian.

Sekarang mari kita cari tahu seberapa simetris kedua gender dalam dataset ini?

 data['Gender'].value_counts() >> Male 5000 Female 5000 Name: Gender, dtype: int64 

Idealnya dibagi rata. Dan ini bagus, karena jika ada: 9999 pria dan 1 wanita, maka tidak akan ada gunanya berpura-pura bahwa DataSet ini mengungkapkan kedua jenis kelamin dengan sama baiknya. Dalam kasus kami, semuanya baik-baik saja!

Bagi dan pelajari!

Sekarang intuisi menunjukkan bahwa akan benar untuk memisahkan kedua jenis kelamin dan mengeksplorasi secara terpisah. Memang, dalam kehidupan kita sering melihat bahwa pria dan wanita memiliki plus dan minus tinggi dan berat yang berbeda

 #  data_male = data[data['Gender'] == 'Male'].copy() #  data_female = data[data['Gender'] == 'Female'].copy() 

Mari kita lihat statistik deskriptif kecil yang ditawarkan modul panda kepada kita.

Pria :

 data_male.describe() 

Wanita :

 data_female.describe() 

Kita melihat bahwa pada pria rata - rata dan median adalah 175cm dan 85kg. Dan pada wanita : 162cm dan 62kg. Ini memberitahu kita bahwa tidak ada emisi yang kuat. Atau mereka simetris di kedua sisi median. Sangat jarang.

Tetapi kedua jenis kelamin memiliki sedikit penyimpangan dari rata-rata dari median. Tetapi mereka tidak signifikan dan mereka hanya terlihat pada seratus. Mari kita lanjutkan!

Histogram

Ini adalah grafik yang memplot nilai dari minimum ke maksimum dalam urutan pertumbuhan, dan menunjukkan jumlah instance individual.

 fig, axes = plt.subplots(2,2, figsize=(20,10)) plt.subplots_adjust(wspace=0, hspace=0) axes[0,0].hist(data_male['Height'], label='Male Height', bins=100, color='red') axes[0,1].hist(data_male['Weight'], label='Male Weight', bins=100, color='red', alpha=0.4) axes[1,0].hist(data_female['Height'], label='Female Height', bins=100, color='blue') axes[1,1].hist(data_female['Weight'], label='Female Weight', bins=100, color='blue', alpha=0.4) axes[0,0].legend(loc=2, fontsize=20) axes[0,1].legend(loc=2, fontsize=20) axes[1,0].legend(loc=2, fontsize=20) axes[1,1].legend(loc=2, fontsize=20) plt.savefig('plt_histogram.png') plt.show() 

Data didistribusikan berbentuk lonceng. Sangat mirip dengan distribusi normal .

Selain tes statistik untuk distribusi normal, ada tes visual. Jika distribusi berdasarkan jenis dan logika tampaknya normal - kita dapat mengasumsikan dengan beberapa asumsi bahwa kita sedang berhadapan dengannya.

Seseorang dapat melakukan uji normalitas statistik dan menentukan nilai-p, tetapi Saya tidak bisa ini di luar ruang lingkup artikel.

Belajar bekerja dengan pena

Panda dapat menghitung banyak untuk kita. Tetapi Anda perlu setidaknya sekali menghitung sendiri beberapa statistik. Sekarang saya akan menunjukkan cara menghitung standar deviasi .

Mari kita lakukan pada contoh pria dan karakteristik - pertumbuhan.

Rata-rata

Formula

$$

$$M = \ frac {1} {N} \ jumlah \ limit_ {i = 1} ^ N n_i$$

dimana

• M - nilai rata-rata
• N adalah jumlah instance
• ni - single instance

Kode:

 mean = data_male['Height'].mean() print('mean:\t{:.2f}'.format(mean)) >> mean: 175.33 

Tinggi rata-rata - 175cm

Deviasi kuadrat

$$

$$d_i = (n_i - M) ^ 2$$

dimana

• deviasi tunggal
• ni - single instance
• M - rata-rata

Kode:

 data_male['Height_d'] = (data_male['Height'] - mean) ** 2 data_male['Height_d'].head(10) >> 0 149.927893 1 0.385495 2 166.739089 3 47.193692 4 4.721246 5 20.288347 6 0.375539 7 2.964214 8 25.997623 9 200.149603 Name: Height_d, dtype: float64 

Dispersi

Formula

$$

$$D = \ frac {1} {N} \ jumlah \ limit_ {i = 1} ^ N d_i$$

dimana

• D adalah nilai dispersi
• deviasi tunggal
• N adalah jumlah instance

Kode:

 disp = data_male['Height_d'].mean() print('disp:\t{:.2f}'.format(disp)) >> disp: 52.89 

Dispersi - 53

Simpangan baku

Formula

$$

$$std = \ sqrt {D}$$

dimana

• std - nilai standar deviasi
• D adalah nilai dispersi

Kode:

 std = disp ** 0.5 print('std:\t{:.2f}'.format(std)) >> std: 7.27 

Standar Deviasi - 7

Interval Keyakinan

Sekarang kita akan menemukan kisaran pertumbuhan dan berat badan 68%, 95% dan 99,7% pria dan wanita .

Ini tidak begitu sulit - Anda perlu menambah dan mengurangi standar deviasi dari rata-rata. Ini terlihat seperti ini:

• 68% - plus atau minus satu standar deviasi
• 95% - plus atau minus dua standar deviasi
• 99,7% - plus atau minus tiga standar deviasi

Kami menulis fungsi bantu yang akan mempertimbangkan ini:

 def get_stats(series, title='noname'): #    print('= {} =\n'.format(title.upper())) #     pandas descr = series.describe() #   mean = descr['mean'] print('= Mean:\t{:.0f}'.format(mean)) #    std = descr['std'] print('= Std:\t{:.0f}'.format(std)) #    print('\n= = = =\n') #   ## 68% devi_1 = [mean - std, mean + std] ## 95% devi_2 = [mean - 2 * std, mean + 2 * std] ## 99.7% devi_3 = [mean - 3 * std, mean + 3 * std] #   print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1])) print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1])) print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1])) 

Nah, terapkan ke data:

Pria | Pertumbuhan

 get_stats(data_male['Height'], title='Male Height') >> = MALE HEIGHT = = Mean: 175 = Std: 7 = = = = = 68% is from 168 to 183 = 95% is from 161 to 190 = 99.7% is from 154 to 197 

Pria | Berat

 get_stats(data_male['Height'], title='Male Height') >> = MALE WEIGHT = = Mean: 85 = Std: 9 = = = = = 68% is from 76 to 94 = 95% is from 67 to 103 = 99.7% is from 58 to 112 

Wanita | Pertumbuhan

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE HEIGHT = = Mean: 162 = Std: 7 = = = = = 68% is from 155 to 169 = 95% is from 148 to 176 = 99.7% is from 141 to 182 

Wanita | Berat

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE WEIGHT = = Mean: 62 = Std: 9 = = = = = 68% is from 53 to 70 = 95% is from 44 to 79 = 99.7% is from 36 to 87 

Karena itu kesimpulannya:

• Kebanyakan pria: 154cm - 197cm dan 58kg - 112kg.
• Sebagian besar wanita: 141cm - 182cm dan 36kg - 87kg.

Sekarang tinggal menerapkan pembelajaran mesin pada perangkat ini dan mencoba memprediksi bobot berdasarkan tinggi.

Tetangga terdekat

Algoritma "Untuk tetangga terdekat" sederhana. Ada untuk tugas klasifikasi - untuk membedakan kucing dari anjing - dan untuk tugas-tugas regresi - untuk menebak berat dengan tinggi. Inilah yang kami butuhkan!

Untuk regresi, ia menggunakan algoritma berikut:

• Mengingat semua titik data
• Ketika sebuah titik baru muncul, ia mencari K tetangganya yang terdekat (angka K ditetapkan oleh pengguna)
• Rata-rata hasilnya
• Memberi jawaban

Pertama, Anda perlu membagi set data ke dalam bagian pelatihan dan tes dan menguji algoritma

Bereksperimen dengan pria

 X_train, X_test, y_train, y_test = train_test_split(data_male['Height'], data_male['Weight']) 

Terbagi, sekarang saatnya untuk mencoba.

 #   knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8298400793623182 #   knr5 = KNeighborsRegressor(n_neighbors=5) knr5.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr5.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7958051642678619 #   knr7 = KNeighborsRegressor(n_neighbors=7) knr7.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr7.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7769249318420969 

Kami tidak akan pergi jauh dan berhenti di tiga tetangga. Tetapi pertanyaannya adalah: bisakah model seperti itu menebak berat badan saya?

 knr3.predict([[180]])[0, 0] >> 88.67596236265881 

88kg sangat dekat. Yang kedua, berat badan saya 89,8kg

Grafik prediksi untuk pria

Waktu untuk membangun bagian favorit saya dalam sains adalah grafik.

 array_male = [] #   99.7% xaxis = range(154, 198) for h in xaxis: ans = knr3.predict([[h]]) array_male.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male, 'r-', linewidth=4) plt.title('Male heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_male.png') plt.show() 

Model dan grafik prediksi untuk wanita

 X_train, X_test, y_train, y_test = train_test_split(data_female['Height'], data_female['Weight']) knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8135681584074799 

 array_female = [] #   99.7% xaxis = range(141, 183) for h in xaxis: ans = knr3.predict([[h]]) array_female.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_female, 'b-', linewidth=4) plt.title('Female heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_female.png') plt.show() 

Dan tentu saja menarik bagaimana grafik ini terlihat bersama:

 #      xaxis = range(154, 183) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male[:-15], 'r-', linewidth=4) plt.plot(xaxis, array_female[13:], 'b-', linewidth=4) plt.title('Together heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_together.png') plt.show() 

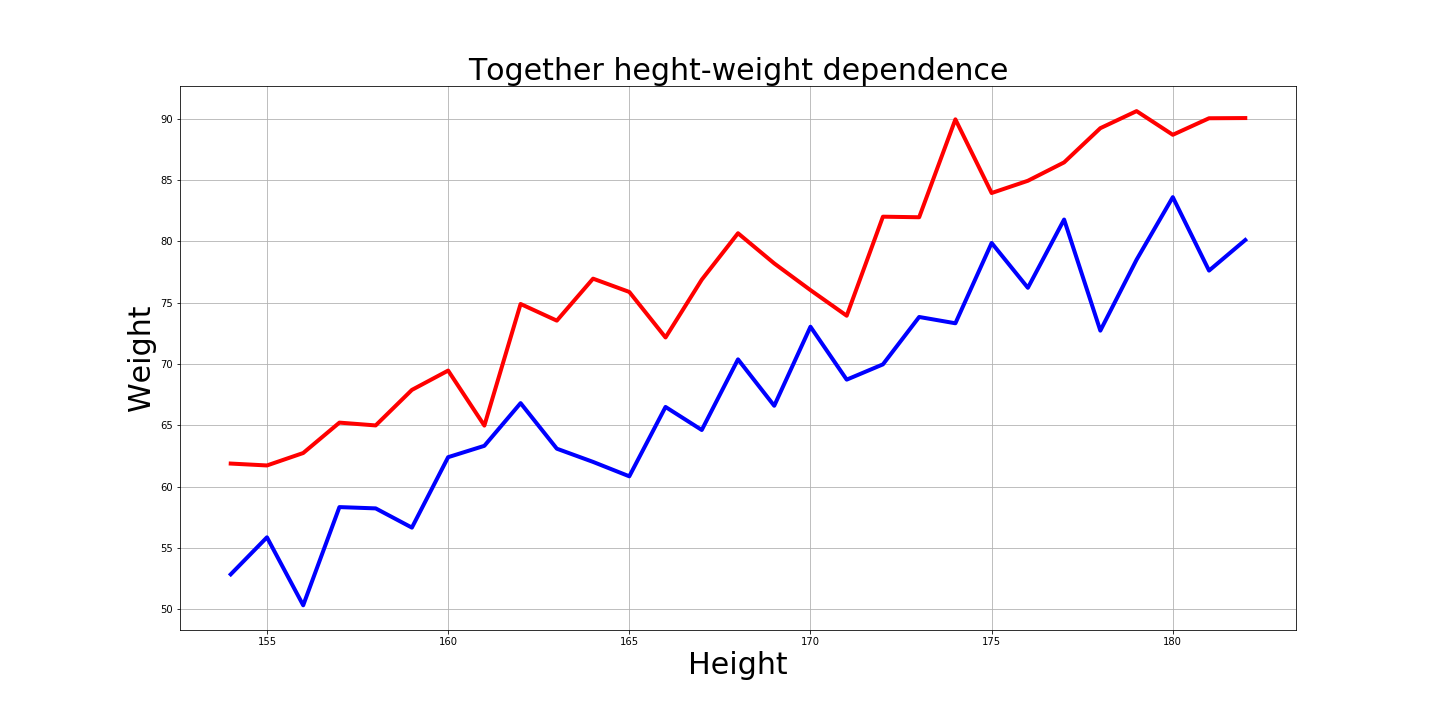
Jawaban atas pertanyaan

- Berapa kisaran berat dan tinggi badan untuk sebagian besar pria dan wanita?

99,7% pria: dari 154cm hingga 197cm dan dari 58kg ke 112kg.
Dan 99,7% wanita: dari 141cm ke 182cm dan dari 36kg ke 87kg.

- Pria "rata-rata" dan wanita "rata-rata" seperti apa mereka?

Pria rata-rata adalah 175cm dan 85kg.
Dan rata-rata wanita adalah 162cm dan 62kg.

- Akankah model pembelajaran mesin KNN sederhana dari data ini memprediksi bobot berdasarkan tinggi?

Ya, modelnya diprediksi 88kg, dan saya punya 89,8kg.

Semua yang saya lakukan, saya kumpulkan di sini

Kontra artikel

• Tidak ada deskripsi DataSet. Mungkin, usia dan faktor lain pada orang berbeda. Karena itu, seseorang tidak dapat menerimanya dengan iman, tetapi hanya demi percobaan - tolong.
• Dalam cara yang baik - perlu untuk melakukan uji normalitas distribusi

Epilog

Seperti jika Anda mencapai interval 99,7%