ClickHouse terus-menerus menghadapi tugas pemrosesan string. Misalnya, mencari, menghitung properti string UTF-8, atau sesuatu yang lebih eksotis, apakah itu pencarian case-sensitive atau pencarian data terkompresi.
Semuanya dimulai dengan fakta bahwa manajer pengembangan ClickHouse Lyosha Milovidov o6CuFl2Q datang kepada kami di Fakultas Ilmu Komputer di Sekolah Tinggi Ekonomi dan menawarkan sejumlah besar topik untuk makalah dan diploma. Ketika saya melihat "Algoritma Pemrosesan String Cerdas di ClickHouse" (Saya, seseorang yang tertarik pada berbagai algoritma, termasuk yang eksperimental), saya segera menyiapkan rencana untuk bagaimana membuat diploma paling keren. Kegembiraan dan ekspresi saya dapat digambarkan sebagai berikut:

Clickhouse
ClickHouse dengan hati-hati memikirkan organisasi penyimpanan data dalam memori - dalam kolom. Pada akhir setiap kolom ada padding 15 byte untuk membaca register 16-byte yang aman. Misalnya, ColumnString menyimpan string yang diakhiri null bersama dengan offset. Sangat mudah untuk bekerja dengan array seperti itu.

Ada juga ColumnFixedString, ColumnConst dan LowCardinality, tetapi kami tidak akan membicarakannya secara mendetail hari ini. Poin utama pada titik ini adalah bahwa desain pembacaan yang aman untuk ekornya baik-baik saja, dan lokasi data juga memainkan peran dalam pemrosesan.
Pencarian Substring
Kemungkinan besar, Anda tahu banyak algoritma berbeda untuk menemukan substring dalam string. Kami akan berbicara tentang yang digunakan di ClickHouse. Pertama, kami memperkenalkan beberapa definisi:
- tumpukan jerami - garis di mana kita melihat; panjang biasanya dilambangkan dengan n .
- jarum - string atau ekspresi reguler yang kita cari; panjangnya akan dilambangkan dengan m .
Setelah mempelajari sejumlah besar algoritma, saya dapat mengatakan bahwa ada 2 (maksimal 3) jenis algoritma pencarian substring. Yang pertama adalah penciptaan dalam satu bentuk atau lain dari struktur sufiks. Tipe kedua adalah algoritma berdasarkan perbandingan memori. Ada juga algoritma Rabin-Karp, yang menggunakan hash, tetapi cukup unik dalam jenisnya. Algoritma tercepat tidak ada, semuanya tergantung pada ukuran alfabet, panjang jarum, tumpukan jerami dan frekuensi kemunculannya.
Baca tentang berbagai algoritma di sini . Dan berikut ini adalah algoritma yang paling populer:
- Knut - Morris - Pratt,
- Boyer - Moore,
- Boyer - Moore - Horspool,
- Rabin - Carp,
- Dua sisi (digunakan dalam glibc yang disebut "memmem"),
- BNDM
Daftarnya berlanjut. Kami di ClickHouse dengan jujur mencoba segalanya, tetapi pada akhirnya kami memilih versi yang lebih luar biasa.
Algoritma Volnitsky
Algoritma ini diterbitkan di blog programmer Leonid Volnitsky pada akhir 2010. Ini agak mengingatkan pada algoritma Boyer-Moore-Horspool, hanya versi yang ditingkatkan.
Jika m <4 , maka algoritma pencarian standar digunakan. Simpan semua jarum bigrams (2 byte berturut-turut) dari ujung ke tabel hash dengan pengalamatan terbuka ukuran | Sigma | 2 elemen (dalam praktiknya, ini adalah 2 16 elemen), di mana offset bigram ini akan menjadi nilainya, dan bigram itu sendiri akan menjadi hash dan indeks pada saat yang sama. Posisi awal akan berada di posisi m - 2 dari awal tumpukan jerami. Kami mengikuti tumpukan jerami dengan langkah m - 1 , melihat bigram berikutnya dari posisi ini di tumpukan jerami dan mempertimbangkan semua nilai dari bigram di tabel hash. Kemudian kita akan membandingkan dua buah memori dengan algoritma perbandingan biasa. Ekor yang tersisa akan diproses oleh algoritma yang sama.
Langkah m - 1 dipilih sedemikian rupa sehingga jika ada jarum di tumpukan jerami, maka kami pasti akan mempertimbangkan bigram entri ini - dengan demikian memastikan bahwa kami mengembalikan posisi entri di tumpukan jerami. Kejadian pertama dijamin oleh fakta bahwa kami menambahkan indeks dari ujung ke tabel hash oleh bigram. Ini berarti bahwa ketika kita bergerak dari kiri ke kanan, pertama kita akan mempertimbangkan bigrams dari akhir baris (mungkin awalnya mempertimbangkan bigrams yang sama sekali tidak perlu), kemudian lebih dekat ke awal.
Pertimbangkan sebuah contoh. Biarkan tumpukan jerami tali menjadi abacabaac dan jarum sama dengan aaca . Tabel hash adalah {aa : 0, ac : 1, ca : 2} .
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Kami melihat ac bigram. Di jarum itu, kami menggantikan dalam kesetaraan:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
Tidak cocok Setelah ac tidak ada entri di tabel hash, kita langkah dengan langkah 3:
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Tidak ada bigrams ba di tabel hash, silakan:
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Ada jarum bigram di jarum, kita melihat offset dan menemukan entri:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
Algoritme memiliki banyak keunggulan. Pertama, Anda tidak perlu mengalokasikan memori di heap, dan 64 KB di stack bukan sesuatu yang transendental sekarang. Kedua, 2 16 adalah angka yang sangat baik untuk mengambil modulo untuk prosesor; ini hanya instruksi movzwl (atau, seperti yang kita bercanda, “movsvl”) dan keluarga.
Rata-rata, algoritma ini terbukti menjadi yang terbaik. Kami mengambil data dari Yandex.Metrica, permintaannya hampir nyata. Satu aliran kecepatan, lebih banyak lebih baik, KMP: Algoritma Knut - Morris - Pratt, BM: Boyer - Moore, BMH: Boyer - Moore - Horspool.
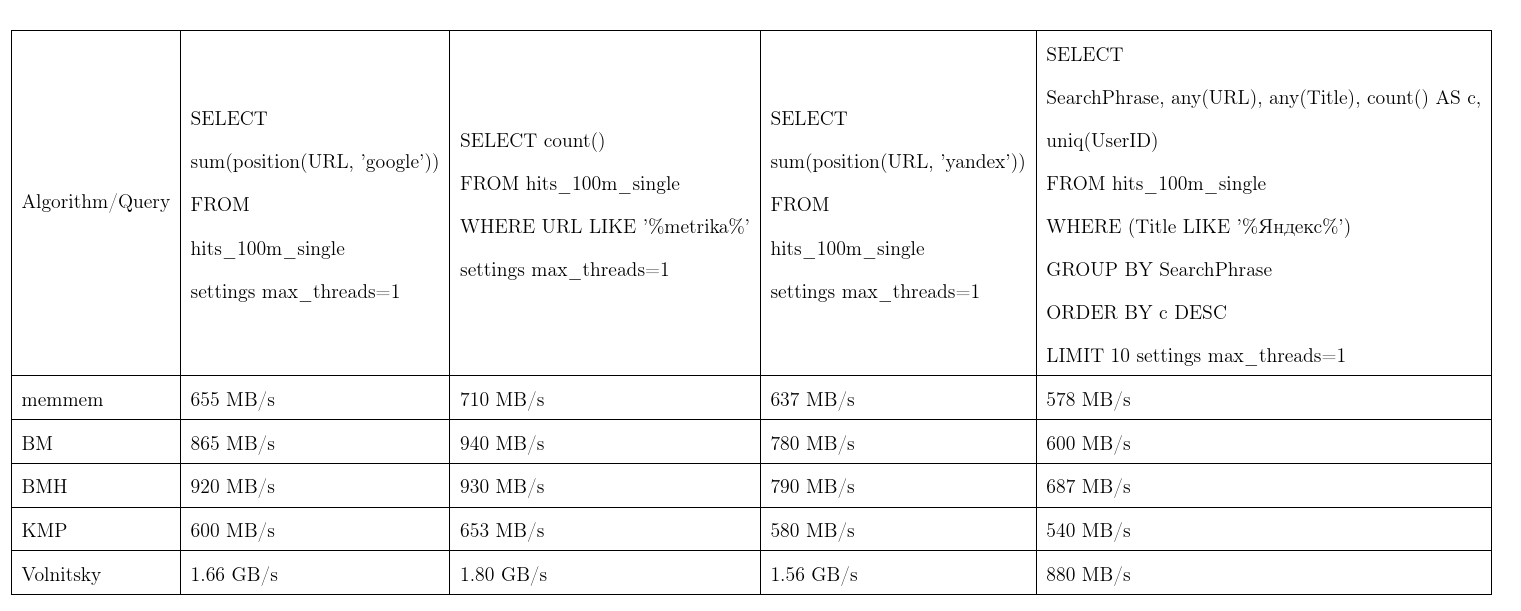
Agar tidak berdasar, algoritme dapat bekerja waktu kuadratik:

Ini digunakan dalam fungsi position(Column, ConstNeedle) , dan juga bertindak sebagai optimisasi untuk pencarian ekspresi reguler.
Pencarian Ekspresi Reguler
Kami akan memberi tahu Anda bagaimana ClickHouse mengoptimalkan pencarian ekspresi reguler. Banyak ekspresi reguler mengandung substring di dalam, yang harus di dalam tumpukan jerami. Agar tidak membangun mesin status terbatas dan mengeceknya, kami akan mengisolasi substring tersebut.
Untuk melakukan ini cukup sederhana: setiap tanda kurung buka menambah tingkat sarang, setiap tanda kurung tutup akan berkurang; ada juga karakter khusus untuk ekspresi reguler (mis. '.', '*', '?', '\ w', dll.). Kita perlu mendapatkan semua substring di level 0. Pertimbangkan sebuah contoh:
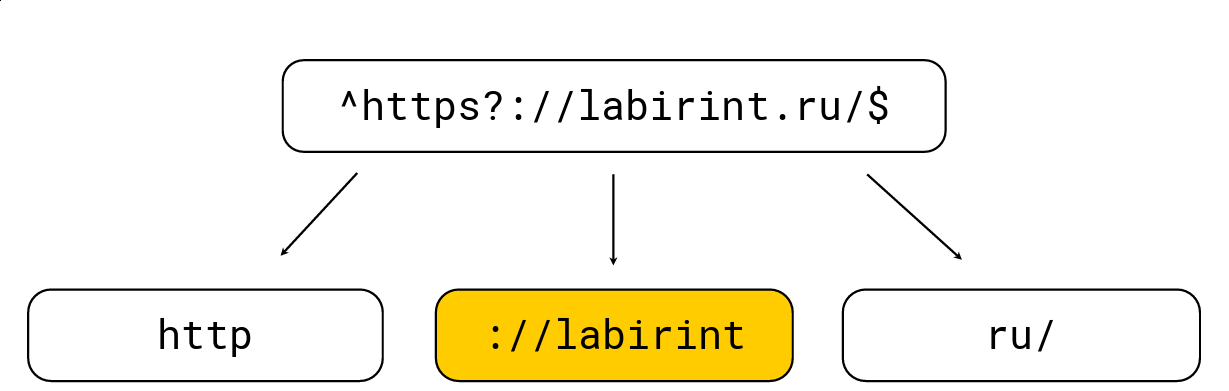
Kami memecahnya menjadi substring yang harus ada di tumpukan jerami dari ekspresi reguler, setelah itu kami memilih panjang maksimum, mencari kandidat di atasnya dan kemudian memeriksa dengan mesin ekspresi reguler biasa RE2. Pada gambar di atas terdapat ekspresi reguler, diproses oleh mesin RE2 biasa pada 736 MB / s, Hyperscan (sekitar beberapa saat kemudian) mengelola menjadi 1,6 GB / s, dan kami mengelola 1,69 GB / s per inti bersama dengan dekompresi LZ4. Secara umum, pengoptimalan seperti itu ada di permukaan dan sangat mempercepat pencarian untuk ekspresi reguler, tetapi seringkali tidak diimplementasikan dalam alat, yang sangat mengejutkan saya.
Kata kunci LIKE juga dioptimalkan menggunakan algoritma ini, hanya setelah LIKE dapat ekspresi reguler yang sangat disederhanakan melalui %%%%% (substring sewenang-wenang) dan _ (karakter sewenang-wenang).
Sayangnya, tidak semua ekspresi reguler mengalami optimasi seperti itu, misalnya, dari yandex|google tidak mungkin untuk secara eksplisit mengisolasi substring yang harus terjadi di tumpukan jerami. Oleh karena itu, kami datang dengan solusi yang sangat berbeda.
Cari banyak substring
Masalahnya adalah ada banyak jarum, dan saya ingin mengerti jika setidaknya satu dari mereka termasuk dalam tumpukan jerami. Ada metode yang cukup klasik untuk pencarian seperti itu, misalnya, algoritma Aho-Korasik. Tapi dia tidak terlalu cepat untuk tugas kami. Kami akan membicarakannya nanti.
Lesha ClickHouse menyukai solusi non-standar, jadi kami memutuskan untuk mencoba sesuatu yang berbeda dan, mungkin, membuat algoritma pencarian baru sendiri. Dan mereka melakukannya.
Kami melihat algoritma Volnitsky dan memodifikasinya sehingga mulai mencari banyak substring sekaligus. Untuk melakukan ini, Anda hanya perlu menambahkan bigrams dari semua baris dan menyimpan indeks baris di tabel hash. Langkah ini akan dipilih dari setidaknya semua panjang jarum minus 1 untuk menjamin properti lagi bahwa jika ada kejadian kita akan melihat bigram nya. Tabel hash akan tumbuh hingga 128 KB (garis lebih panjang dari 255 diproses oleh algoritma standar, kami akan mempertimbangkan tidak lebih dari 256 jarum). Saya sangat malas, jadi ini adalah contoh dari presentasi (baca dari kiri ke kanan dari atas ke bawah):


Kami mulai melihat bagaimana suatu algoritma berperilaku dibandingkan dengan yang lain (baris diambil dari data nyata). Dan untuk sejumlah kecil jalur, ia melakukan segalanya (kecepatan dan pembongkaran ditunjukkan - sekitar 2,5 GB / s).
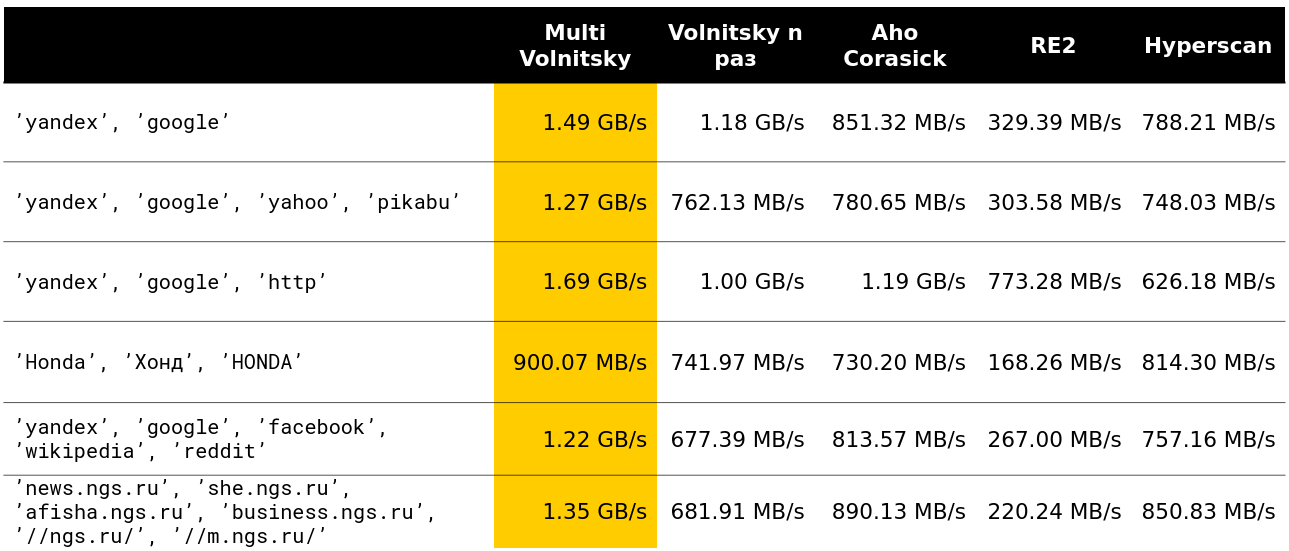
Kemudian menjadi menarik. Misalnya, dengan sejumlah besar bigrams serupa, kami kalah dari beberapa pesaing. Dapat dimengerti - kita mulai membandingkan banyak keping memori dan menurunkan.

Anda tidak dapat berakselerasi banyak jika panjang minimum jarum cukup besar. Jelas, kami memiliki lebih banyak peluang untuk melewatkan seluruh tumpukan jerami tanpa membayar apa pun untuk itu.

Titik kritis dimulai di suatu tempat pada baris 13-15. Sekitar 97% dari permintaan yang saya lihat di cluster kurang dari 15 baris:
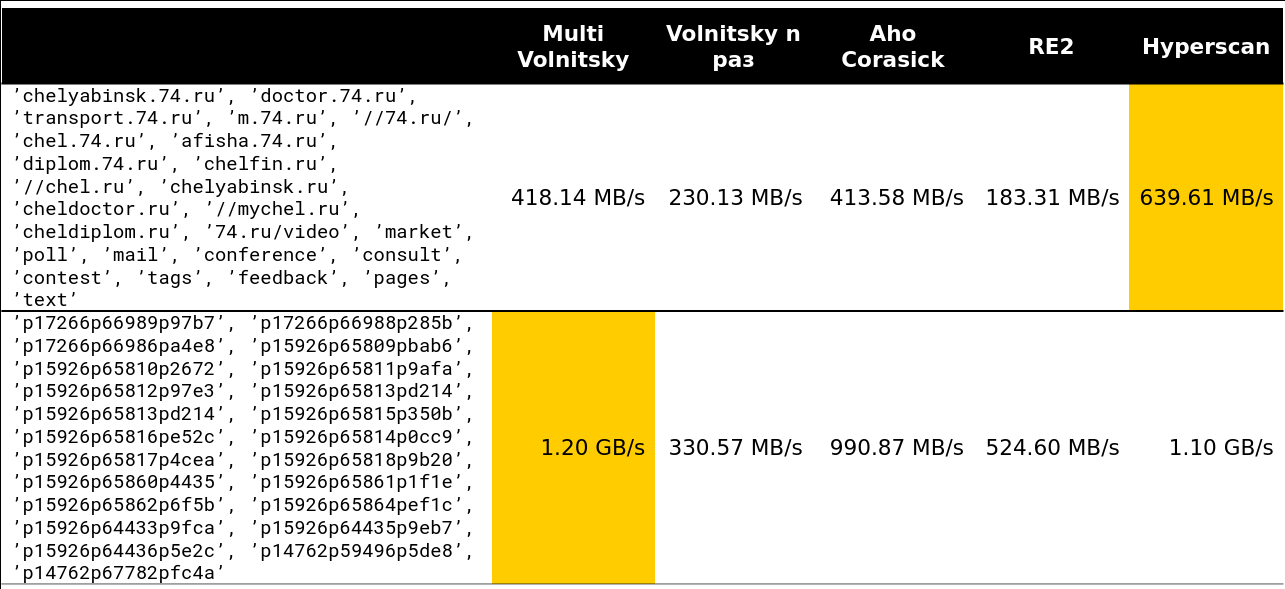
Nah, gambar yang sangat menyeramkan - 41 baris, banyak bigrams berulang:

Akibatnya, di ClickHouse (19.5) kami menerapkan fungsi berikut melalui algoritma ini:
- multiSearchAny(h, [n_1, ..., n_k]) - 1, jika setidaknya salah satu jarum ada di tumpukan jerami.
- multiSearchFirstPosition(h, [n_1, ..., n_k]) - posisi paling kiri dari entri ke tumpukan jerami (dari satu) atau 0 jika tidak ditemukan.
- multiSearchFirstIndex(h, [n_1, ..., n_k]) - indeks jarum paling kiri, yang ditemukan di tumpukan jerami; 0 jika tidak ditemukan.
- multiSearchAllPositions(h, [n_1, ..., n_k]) - semua posisi pertama dari semua jarum, mengembalikan sebuah array.
Sufiksnya adalah -UTF8 (kami tidak menormalkan), -CaseInsensitive (kami menambahkan 4 bigrams dengan case yang berbeda), -CaseInsensitiveUTF8 (ada kondisi bahwa huruf besar dan huruf kecil harus memiliki jumlah byte yang sama). Lihat implementasinya di sini .
Setelah itu, kami bertanya-tanya apakah kami bisa melakukan sesuatu yang mirip dengan banyak ekspresi reguler. Dan mereka menemukan solusi yang sudah rusak dalam tolok ukur.
Cari berdasarkan banyak ekspresi reguler
Hyperscan adalah perpustakaan dari Intel yang segera mencari banyak ekspresi reguler. Ia menggunakan heuristik untuk mengisolasi subword dari ekspresi reguler yang kami tulis, dan banyak SIMD untuk mencari automaton Glushkov (algoritmenya tampaknya disebut Teddy).
Secara umum, semuanya ada dalam tradisi terbaik untuk mendapatkan hasil maksimal dari pencarian ekspresi reguler. Perpustakaan benar-benar melakukan apa yang dideklarasikan dalam fungsinya.

Untungnya, dalam bulan pengembangan saya di ClickHouse, saya bisa menyalip pengembangan 12 tahun pada kelas pertanyaan yang layak dan saya sangat senang dengan ini.
Di Yandex, perpustakaan Hyperscan juga digunakan di antispam. Dilihat oleh ulasan, dia dengan tenang memproses ribuan ekspresi reguler dan dengan cepat mencari mereka.
Perpustakaan memiliki beberapa kelemahan. Yang pertama adalah jumlah memori yang tidak berdokumen yang dikonsumsi dan fitur aneh bahwa tumpukan jerami harus kurang dari 2 32 byte. Yang kedua - Anda tidak dapat mengembalikan posisi pertama secara gratis, indeks jarum paling kiri, dll. Dan minus ketiga - ada beberapa bug yang tiba-tiba. Oleh karena itu, di ClickHouse, kami menerapkan fungsi-fungsi berikut menggunakan Hyperscan:
- multiMatchAny(h, [n_1, ..., n_k]) - 1, jika setidaknya salah satu jarum muncul dengan tumpukan jerami.
- multiMatchAnyIndex(h, [n_1, ..., n_k]) - indeks apa pun dari jarum yang multiMatchAnyIndex(h, [n_1, ..., n_k]) tumpukan jerami.
Kami tertarik, tetapi bagaimana Anda bisa mencari tidak persis, tetapi kira-kira? Dan datang dengan beberapa solusi.
Perkiraan pencarian
Standar dalam pencarian perkiraan adalah jarak Levenshtein - jumlah minimum karakter yang dapat diganti, ditambahkan dan dihapus untuk mendapatkan string b panjang n dari string a panjang m. Sayangnya, algoritma pemrograman dinamis naif bekerja untuk O (mn) ; pikiran terbaik ShAD dapat melakukannya dalam O (mn / log max (n, m)) ; mudah untuk memikirkan O ((n + m) ⋅ alpha) , di mana alpha adalah jawabannya; sains dapat melakukannya untuk O ((alfa - | n - m |) min (m, n, alfa) + m + n) (algoritmanya sederhana, baca setidaknya di ShAD) atau, jika sedikit lebih jelas, untuk O (alfa ^ 2 + m + n) . Masih ada yang minus: kemungkinan besar tidak mungkin untuk membuang waktu kuadrat dalam kasus terburuk secara polinomi - Peter Indik menulis artikel yang sangat kuat tentang ini.
Ada latihan: bayangkan bahwa untuk mengganti karakter dalam jarak Levenshtein Anda membayar denda bukan dua, tetapi dua; kemudian muncul dengan algoritma untuk O ((n + m) log (n + m)) .
Masih tidak berfungsi, terlalu lama dan mahal. Tetapi dengan bantuan jarak seperti itu, kami melakukan deteksi kesalahan ketik di kueri.
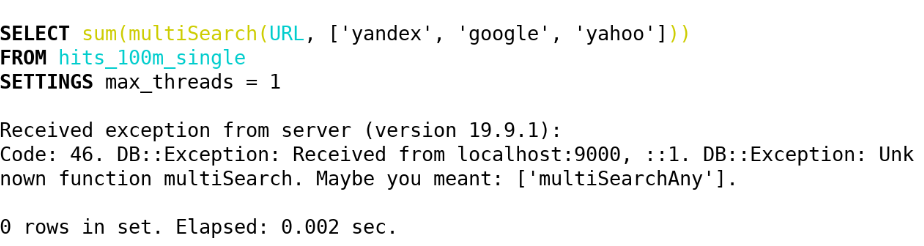
Selain jarak Levenshtein, ada jarak Hamming. Dengan dia juga, semuanya sangat buruk, tetapi sedikit lebih baik daripada dengan jarak Levenshtein. Itu tidak memperhitungkan penghapusan karakter, tetapi hanya mempertimbangkan untuk dua baris dengan panjang yang sama jumlah karakter di mana mereka berbeda. Oleh karena itu, jika kita menggunakan jarak untuk string dengan panjang m <n, maka hanya dalam mencari substring terdekat.
Bagaimana menghitung array perbedaan tersebut (array d dari n - m + 1 elemen, di mana d [i] adalah jumlah karakter yang berbeda di i-th dari awal overlay) untuk O (| Sigma | (n + m) log (n + m) ) ? Pertama, lakukan | Sigma | topeng bit yang menunjukkan apakah simbol ini sama dengan yang dianggap. Selanjutnya, kami menghitung jawaban untuk masing-masing topeng Sigma dan menambahkan - kami mendapatkan jawaban asli.
Pertimbangkan sebuah contoh. abba , substring ba , alfabet biner. Kami mendapatkan 2 topeng 1001, 01 dan 0110, 10 .
a 1001 01 - 0 01 - 0 01 - 1
b 0110 10 - 0 10 - 1 10 - 1
Kami mendapatkan array [0, 1, 2] - ini adalah jawaban yang hampir benar. Tetapi perhatikan bahwa untuk setiap huruf, jumlah korek api hanyalah produk skalar dari jarum biner tetap dan semua substring tumpukan jerami. Dan untuk ini, tentu saja, ada transformasi Fourier yang cepat!
Bagi mereka yang tidak tahu: FFT dapat melipatgandakan dua polinomial derajat m <n untuk waktu O (n log n) , dengan ketentuan bahwa pekerjaan dengan koefisien dilakukan per satuan waktu. Konvolusi sangat mirip dengan produk skalar. Cukup untuk menduplikasi koefisien dari polinomial pertama, dan memperluas dan menambah yang kedua dengan jumlah nol yang diperlukan, maka kita mendapatkan semua produk skalar dari satu string biner dan semua substring yang lain di O (n log n) - semacam sihir! Tapi percayalah, ini benar-benar nyata, dan terkadang orang melakukannya.
Tetapi tidak di ClickHouse. Bagi kami, bekerja dengan | Sigma | = 30 sudah besar, dan FFT bukan algoritma praktis yang paling menyenangkan untuk prosesor atau, seperti yang dikatakan orang awam, "konstanta besar."
Karena itu, kami memutuskan untuk melihat metrik lain. Kami sampai ke bioinformatika, di mana orang menggunakan jarak n-gram. Faktanya, kita mengambil semua n-gram tumpukan jerami dan jarum, pertimbangkan 2 multiset dengan n-gram ini. Kemudian kita mengambil perbedaan simetris dan membaginya dengan jumlah kardinalitas dua multiset dengan n-gram. Kami mendapatkan angka dari 0 hingga 1 - semakin dekat ke 0, semakin banyak garis yang serupa. Pertimbangkan contoh di mana n = 4 :
abcda → {abcd, bcda}; Size = 2 bcdab → {bcda, cdab}; Size = 2 . |{abcd, cdab}| / (2 + 2) = 0.5
Sebagai hasilnya, kami membuat jarak 4 gram dan menempel banyak ide dari SSE di sana, dan kami juga sedikit melemahkan implementasi untuk hash double-byte crc32.
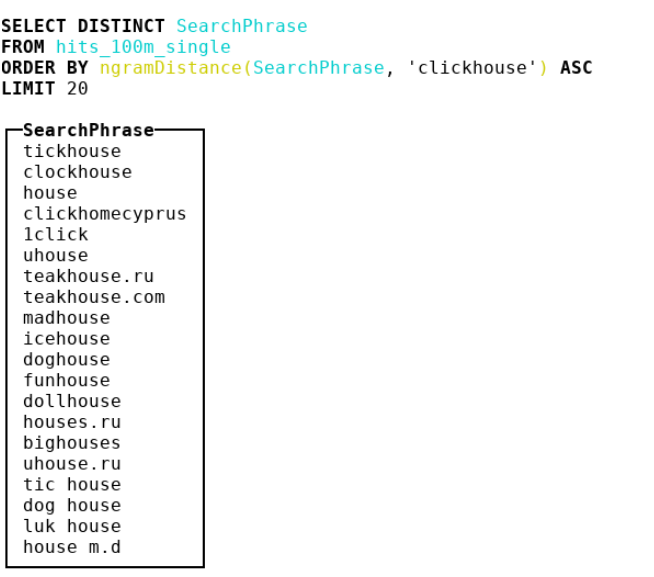
Lihat implementasinya . Perhatian: kode yang sangat menarik dan dioptimalkan untuk kompiler.
Saya terutama menyarankan Anda untuk memperhatikan hack kotor untuk casting huruf kecil untuk ASCII dan poin kode Rusia.
- ngramDistance(haystack, needle) - mengembalikan angka dari 0 hingga 1; semakin dekat ke 0, semakin banyak garis yang mirip satu sama lain.
- -UTF8, -CaseInsensitive, -CaseInsensitiveUTF8 (hack kotor untuk Rusia dan ASCII).
Hyperscan juga tidak berdiri diam - ini memiliki fungsi untuk pencarian perkiraan: Anda dapat mencari garis yang terlihat seperti ekspresi reguler dengan jarak konstan Levenshtein. Sebuah jarak + 1 otomat dibuat, yang saling berhubungan dengan menghapus, mengganti atau menyisipkan karakter, yang berarti "baik", setelah itu algoritma yang biasa untuk memeriksa apakah suatu otomat menerima suatu garis tertentu diterapkan. Di ClickHouse, kami menerapkannya dengan nama-nama berikut:
- multiFuzzyMatchAny(haystack, distance, [n_1, ..., n_k]) - mirip dengan multiMatchAny, hanya dengan jarak.
- multiFuzzyMatchAnyIndex(haystack, distance, [n_1, ..., n_k]) - mirip dengan multiMatchAnyIndex, hanya dengan jarak.
Dengan meningkatnya jarak, kecepatan mulai menurun drastis, tetapi masih tetap pada tingkat yang cukup baik.
Selesaikan pencarian dan mulai memproses string UTF-8. Ada juga banyak hal menarik.
Pemrosesan jalur UTF-8
Saya akui bahwa sulit untuk menerobos langit-langit implementasi naif dalam string yang dikodekan UTF-8. Terutama sulit untuk mengacaukan SIMD. Saya akan membagikan beberapa ide tentang bagaimana melakukan ini.
Ingat seperti apa urutan UTF-8 yang valid:
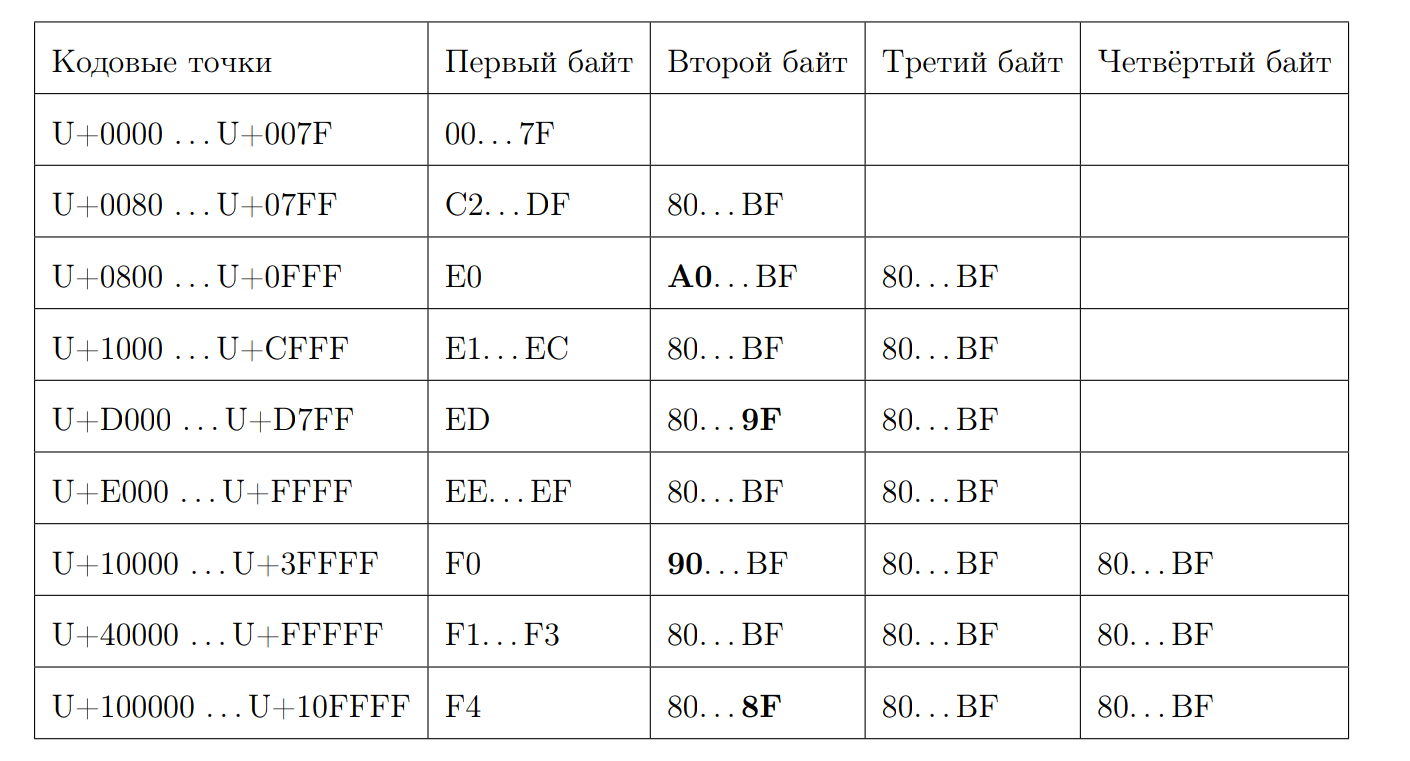
Mari kita coba menghitung panjang titik kode dengan byte pertama. Di sinilah bit bit dimulai. Sekali lagi kami menulis beberapa properti:
- Mulai dari 0xC dan pada 0xD memiliki 2 byte
- 0xC2 = 11 0 00010
- 0xDF = 11 0 11111
- 0xE0 = 111 0 0000
- 0xF4 = 1111 0 100, tidak ada yang lebih jauh dari 0xF4, tetapi jika ada 0xF8, akan ada cerita yang berbeda
- Jawab 7 dikurangi posisi nol pertama dari akhir, jika bukan karakter ASCII
Kami menghitung panjangnya:
inline size_t seqLength(const UInt8 first_octet) { if (first_octet < 0x80u) return 1; const auto first_zero = bitScanReverse(static_cast<UInt8>(~first_octet)); return 7 - first_zero; }
Untungnya, kami memiliki instruksi stok yang dapat menghitung jumlah nol bit, dimulai dengan yang paling signifikan.
f = __builtin_clz(val)
Hitung bitScanReverse:
unsigned int bitScanReverse(unsigned int x) { return 31 - __builtin_clz(x); }
Mari kita coba menghitung panjang string UTF-8 berdasarkan poin kode melalui SIMD. Untuk melakukan ini, lihat setiap byte sebagai nomor yang ditandatangani dan catat properti berikut:
- 0xBF = -65
- 0x80 = -128
- 0xC2 = -62
- 0x7F = 127
- semua byte pertama ada di [0xC2, 0x7F]
- semua byte non-pertama dalam [0x80, 0xBF]
Algoritma ini cukup sederhana. Bandingkan setiap byte dengan -65 dan, jika lebih besar dari angka ini, tambahkan satu. Jika kita ingin menggunakan SIMD, maka ini adalah beban biasa 16 byte dari aliran input. Lalu ada perbandingan byte, yang dalam kasus hasil positif akan memberikan byte 0xFF, dan dalam kasus negatif - 0x00. Kemudian instruksi pmovmskb , yang akan mengumpulkan bit tinggi dari setiap byte register. Kemudian jumlah garis bawah meningkat, kami menggunakan intrinsik untuk instruksi SSE4 popcnt. Skema algoritma ini dapat diilustrasikan dengan sebuah contoh:

Ternyata seiring dengan dekompresi, pemrosesan per inti akan menjadi sekitar 1,5 GB / s.
Fungsinya disebut:
- lengthUTF8(string) - mengembalikan panjang string UTF-8 yang dikodekan dengan benar, sesuatu dianggap tidak valid, pengecualian tidak dilemparkan.
Kami melangkah lebih jauh karena kami ingin lebih banyak fungsi dengan pemrosesan string UTF-8. Misalnya, memeriksa validitas dan casting ke ekspresi UTF-8 yang valid.
Untuk memeriksa validitas, saya mengambil https://github.com/cyb70289/utf8/ , diadaptasi untuk ClickHouse (sebenarnya hanya mengubah pemrosesan ekor) dan mendapatkan kecepatan 1,22 GB / s dibandingkan dengan 900 MB / s untuk algoritma naif . Saya tidak akan menjelaskan algoritma itu sendiri, cukup rumit untuk persepsi.
- isValidUTF8(string) - mengembalikan 1 jika string dikodekan dengan benar dengan UTF-8, jika tidak 0.
- toValidUTF8(string) - menggantikan karakter UTF-8 yang tidak valid dengan karakter (U + FFFD). Semua karakter yang tidak valid berturut-turut dikelompokkan menjadi satu karakter pengganti. Tidak ada ilmu roket.
Secara umum, di jalur UTF-8, karena skema statis yang tidak terlalu menyenangkan, selalu sulit untuk menemukan sesuatu yang dioptimalkan dengan baik.
Apa selanjutnya
Biarkan saya mengingatkan Anda bahwa ini adalah tesis saya. Tentu saja, saya membelanya untuk 10/10. Kami sudah pergi bersamanya ke Highload ++ Siberia (meskipun bagi saya sepertinya ia kurang menarik bagi siapa pun). Tonton presentasi . Saya suka bahwa bagian praktis dari tesis ini menghasilkan banyak penelitian yang menarik. Dan ini adalah ijazah itu sendiri. Ini memiliki banyak kesalahan ketik, karena tidak ada yang membacanya. :)
Sebagai bagian dari persiapan diploma, saya melakukan banyak pekerjaan serupa lainnya (tautan mengarah ke permintaan gabungan):
- Fungsi concat Dioptimalkan 2 kali ;
- Membuat format python paling sederhana untuk permintaan ;
- LZ4 yang Dipercepat sebesar 4% ;
- Saya melakukan pekerjaan yang baik pada SIMD untuk ARM dan PPC64LE ;
- Dan dia menyarankan beberapa siswa FCS dengan ijazah di ClickHouse.
Pada akhirnya, ternyata dalam pengalaman saya, setiap bulan Lesha mencoba mengucapkan mantra padaku ClickHouse adalah sistem yang paling menyenangkan untuk menulis kode berkinerja tinggi, di mana ada dokumentasi, komentar, pengembang luar biasa dan dukungan pengembang. ClickHouse mengagumkan, sungguh. Bosan dengan pemindahan format JSON? Datanglah ke Lesha dan minta tugas dari level mana pun - dia akan menyediakannya untuk Anda, dan selama akhir pekan Anda akan mendapatkan kesenangan besar dari menulis kode.
Tetapi dengan semua prestasi ClickHouse dan desainnya, itu mungkin bukan tentang mereka. Tidak terutama di dalamnya.
Saya menjalani studi sarjana selama 4 tahun di FCS, pada bulan Juni saya lulus dari HSE dengan ijazah merah, bekerja selama satu setengah tahun di tim yang luar biasa di Yandex, setelah dipompa dengan baik. Tanpa pengalaman total selama ini dan besi Tidak ada yang tertulis di pos akan berhasil. FCN sangat keren, jika Anda mengambil yang maksimal darinya. Terima kasih kepada Vana Puzyrevsky ivan_puzyrevskiy , Ignat Kolesnichenko, Gleb Evstropov, Max Babenko maxim_babenko untuk pertemuan dalam petualangan lucu saya di FCN. Dan juga terima kasih kepada semua guru yang mengajari saya sesuatu.