"Jika Anda membaca tulisan" kerbau "di kandang gajah, jangan percayai mata Anda" Kozma Prutkov

Dalam artikel sebelumnya tentang desain berorientasi model , ditunjukkan mengapa model objek diperlukan, dan terbukti bahwa tanpa model objek ini orang dapat berbicara tentang desain berbasis model hanya sebagai badai pemasaran, tanpa makna dan tanpa ampun. Tetapi ketika model objek muncul, insinyur yang kompeten selalu memiliki pertanyaan yang masuk akal: bukti apa yang ada bahwa model matematika dari suatu objek sesuai dengan objek nyata.

Salah satu contoh jawaban untuk pertanyaan ini diberikan dalam artikel tentang desain berorientasi model dari penggerak listrik. Pada artikel ini, kami akan mempertimbangkan contoh membuat model untuk sistem pendingin udara penerbangan, melemahkan praktik dengan beberapa pertimbangan umum teoritis.

Membuat model objek yang andal. Teori

Agar tidak menarik karet, saya akan segera memberi tahu Anda tentang algoritma untuk membuat model untuk desain berorientasi model. Ini hanya memiliki tiga langkah sederhana:

Langkah 1. Kembangkan sistem persamaan aljabar-diferensial yang menggambarkan perilaku dinamis dari sistem yang disimulasikan. Sederhana saja jika Anda mengetahui fisika prosesnya. Banyak ilmuwan telah mengembangkan bagi kita hukum fisika dasar dari nama Newton, Brenuli, Navier Stokes dan Shtangels of Compasses dan Rabinovich lainnya.

Langkah 2. Dalam sistem yang dihasilkan, pisahkan set koefisien empiris dan karakteristik objek simulasi yang dapat diperoleh dari pengujian.

Langkah 3. Lakukan tes objek dan sesuaikan model sesuai dengan hasil eksperimen lapangan, sehingga sesuai dengan kenyataan, dengan tingkat detail yang diperlukan.

Seperti yang Anda lihat, hanya dua tiga.

Contoh praktis

Sistem pendingin udara (SCR) di pesawat terhubung ke sistem pemeliharaan tekanan otomatis. Tekanan di pesawat harus selalu lebih besar dari tekanan eksternal, sedangkan laju perubahan tekanan harus sedemikian rupa sehingga pilot dan penumpang tidak berdarah hidung dan telinga. Oleh karena itu, sistem kontrol aliran masuk dan keluar udara penting untuk keselamatan, dan sistem uji mahal diletakkan di atas tanah untuk pengembangannya. Mereka menciptakan suhu dan tekanan ketinggian penerbangan, mereproduksi mode lepas landas dan mendarat di lapangan terbang dengan ketinggian berbeda. Dan pertanyaan tentang pengembangan dan debugging sistem kontrol untuk mata uang keras meningkat ke potensi penuhnya. Berapa lama kita akan menggerakkan bangku tes untuk mendapatkan sistem kontrol yang memuaskan? Jelas, jika kita menyetel model kontrol ke model objek, siklus kerja di bangku tes dapat dikurangi secara signifikan.

Sistem pendingin udara penerbangan terdiri dari penukar panas yang sama dengan sistem termal lainnya. Baterai - itu juga baterai di Afrika, hanya pendingin udara. Tetapi karena keterbatasan massa take-off dan dimensi pesawat, penukar panas dibuat sekompleks mungkin dan seefisien mungkin untuk mentransfer panas sebanyak mungkin dari massa yang lebih rendah. Akibatnya, geometri menjadi sangat aneh. Seperti misalnya dalam kasus yang sedang dipertimbangkan. Gambar 1 menunjukkan penukar panas piring, di mana membran digunakan antara pelat untuk meningkatkan perpindahan panas. Pendingin panas dan dingin bergantian di saluran, sementara arah aliran melintang. Satu pendingin disuplai ke potongan frontal, yang lain ke samping.

Untuk mengatasi masalah kontrol SCR, kita perlu tahu berapa banyak panas yang ditransfer dari satu media ke media lain dalam penukar panas per satuan waktu. Tingkat perubahan suhu tergantung pada ini, yang kami atur.

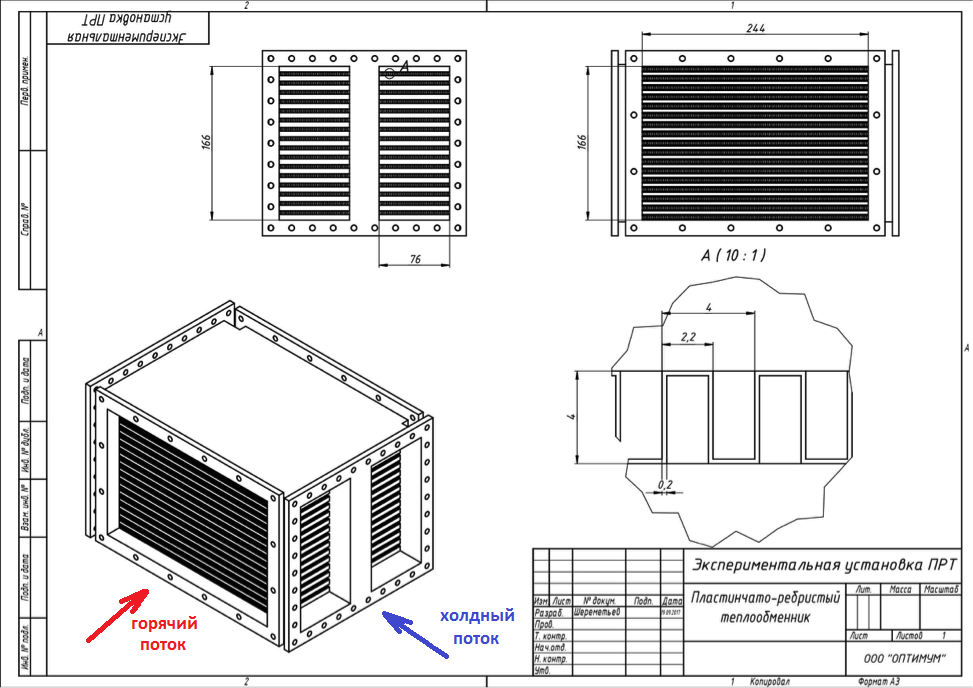
Gambar 1. Diagram penukar panas pesawat.

Masalah pemodelan. Bagian hidrolik

Sekilas, tugasnya cukup sederhana, perlu untuk menghitung aliran massa melalui saluran penukar panas dan aliran panas antara saluran.
Laju aliran massa cairan pendingin dalam saluran dihitung menggunakan rumus Bernoulli:

dimana:
ΔP adalah penurunan tekanan antara dua titik;
ξ adalah koefisien gesekan pendingin;
L adalah panjang saluran;
d adalah diameter hidrolik saluran;
ρ adalah densitas cairan pendingin;
ω adalah kecepatan cairan pendingin dalam saluran.

Untuk saluran dengan bentuk acak, diameter hidrolik dihitung dengan rumus:

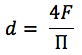
dimana:
F adalah luas lubang;
Perimeter saluran dibasahi P.

Koefisien gesekan dihitung sesuai dengan rumus empiris dan tergantung pada kecepatan aliran dan sifat-sifat pendingin. Untuk geometri yang berbeda, dependensi yang berbeda diperoleh, misalnya, rumus untuk aliran turbulen di pipa halus:

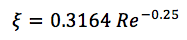
dimana:
Re adalah nomor Reynolds.

Untuk aliran di saluran datar, rumus berikut dapat digunakan:

Dari rumus Bernoulli, Anda dapat menghitung penurunan tekanan untuk kecepatan tertentu, atau sebaliknya, menghitung kecepatan cairan pendingin dalam saluran, berdasarkan penurunan tekanan yang diberikan.

Perpindahan panas

Aliran panas antara cairan pendingin dan dinding dihitung dengan rumus:

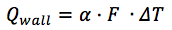
dimana:
α [W / (m2 × deg)] - koefisien perpindahan panas;
F adalah area bore.

Untuk masalah aliran cairan pendingin dalam pipa, sejumlah penelitian telah dilakukan dan ada banyak metode perhitungan, dan sebagai aturan, semuanya bermuara pada ketergantungan empiris, untuk koefisien perpindahan panas α [W / (m2 × deg)]

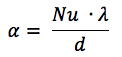
dimana:
Nu adalah nomor Nusselt,
λ adalah konduktivitas termal cairan [W / (m × deg)]
d adalah diameter hidrolik (setara).

Kriteria empiris dependensi digunakan untuk menghitung bilangan Nusselt (kriteria), misalnya, rumus untuk menghitung bilangan Nusselt dari pipa bundar terlihat seperti ini:

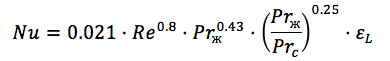
Di sini kita sudah melihat angka Reynolods, angka Prandtl pada suhu dinding dan suhu fluida, dan koefisien ketidakrataan. ( Sumber )

Untuk penukar panas pelat bergelombang, rumusnya mirip ( Sumber ):

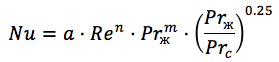
dimana:
n = 0,73 m = 0,43 untuk aliran turbulen,
koefisien a - bervariasi antara 0,065 dan 0,6 tergantung pada jumlah pelat dan rezim aliran.

Perhatikan bahwa koefisien ini dihitung hanya untuk satu titik di aliran. Untuk titik berikutnya, kami memiliki suhu cairan yang berbeda (telah memanas atau dingin), suhu dinding yang berbeda dan, karenanya, semua angka Reynolds dan angka Prandtl mengambang.

Pada titik ini, setiap ahli matematika akan mengatakan bahwa tidak mungkin untuk menghitung dengan tepat sistem di mana koefisien berubah 10 kali, dan ia akan benar.

Setiap insinyur yang berlatih akan mengatakan bahwa setiap penukar panas berbeda dalam pembuatan dan tidak mungkin untuk menghitung sistem, dan itu juga akan benar.

Tapi bagaimana dengan desain berorientasi model? Apakah semuanya hilang?

Penjual canggih perangkat lunak Barat di tempat ini akan memasangkan Anda dengan komputer super dan sistem perhitungan 3D, seperti "tanpa perangkat apa pun." Dan Anda perlu menjalankan perhitungan selama sehari untuk mendapatkan distribusi suhu selama 1 menit.

Jelas bahwa ini bukan pilihan kami, kami perlu men-debug sistem kontrol, jika tidak secara real time, maka setidaknya di masa mendatang.

Metode menyodok

Penukar panas diproduksi, serangkaian pengujian dilakukan, dan tabel efisiensi suhu kondisi-mapan ditetapkan pada laju aliran yang diberikan. Sederhana, cepat dan dapat diandalkan, karena data diperoleh dari tes.

Kerugian dari pendekatan ini adalah bahwa tidak ada karakteristik dinamis dari objek. Ya, kami tahu akan seperti apa fluks panas kondisi-mapan, tetapi kami tidak tahu berapa lama akan terjadi ketika beralih dari satu mode operasi ke mode operasi lainnya.

Oleh karena itu, setelah menghitung karakteristik yang diperlukan, kami membuat sistem kontrol secara langsung selama pengujian, yang ingin kami hindari sejak awal.

Pendekatan Model Berorientasi

Untuk membuat model penukar panas dinamis, perlu menggunakan data uji, untuk menghilangkan ketidakpastian dalam rumus perhitungan empiris - angka Nusselt dan tahanan hidrolik.

Keputusannya sederhana, seperti semua yang cerdik. Kami mengambil rumus empiris, melakukan percobaan dan menentukan nilai koefisien a, sehingga menghilangkan ketidakpastian dalam rumus.

Segera setelah kami memiliki nilai tertentu dari koefisien perpindahan panas, semua parameter lainnya ditentukan oleh hukum fisika dasar konservasi. Perbedaan suhu dan koefisien perpindahan panas menentukan jumlah energi yang ditransfer ke saluran per satuan waktu.

Mengetahui aliran energi, dimungkinkan untuk menyelesaikan persamaan konservasi massa energi dan momentum untuk pendingin di saluran hidrolik. Sebagai contoh, ini:

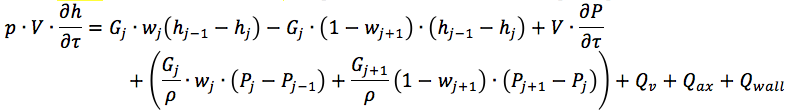
Untuk kasus kami, fluks panas antara dinding dan cairan pendingin - Qwall - tetap tidak ditentukan. Lebih detail dapat ditemukan di sini ...

Dan juga persamaan untuk turunan suhu untuk dinding saluran

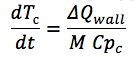
dimana:
ΔQ _wall - perbedaan antara aliran masuk dan keluar ke dinding saluran;
M adalah massa dinding saluran;
C _pc adalah kapasitas panas dari bahan dinding.

Akurasi model

Seperti disebutkan di atas, dalam penukar panas kami memiliki distribusi suhu di atas permukaan pelat. Untuk nilai steady-state, seseorang dapat mengambil rata-rata di atas pelat dan menggunakannya, menghadirkan seluruh penukar panas sebagai satu titik terkonsentrasi, di mana perpindahan panas terjadi di seluruh permukaan penukar panas pada perbedaan suhu yang sama. Namun untuk mode sementara, perkiraan ini mungkin tidak berfungsi. Ekstrem lainnya adalah membuat beberapa ratus ribu poin dan memuat Super Computer, yang juga tidak cocok untuk kita, karena tugasnya adalah mengkonfigurasi sistem kontrol secara real time, atau lebih baik, lebih cepat.

Muncul pertanyaan, berapa banyak bagian yang Anda butuhkan untuk memecahkan penukar panas untuk mendapatkan akurasi dan kecepatan perhitungan yang dapat diterima?

Seperti biasa, saya memiliki model penukar panas amina. Penukar panas adalah sebuah tabung, media pemanas mengalir di dalam pipa, dan dipanaskan di antara lubang-lubang. Untuk menyederhanakan tugas, seluruh tabung penukar panas dapat direpresentasikan sebagai satu pipa setara, dan pipa itu sendiri dapat direpresentasikan sebagai satu set sel desain diskrit, di mana masing-masing model titik perpindahan panas dihitung. Diagram model sel tunggal ditunjukkan pada Gambar 2. Saluran udara panas dan saluran udara dingin dihubungkan melalui dinding yang menyediakan perpindahan panas antar saluran.

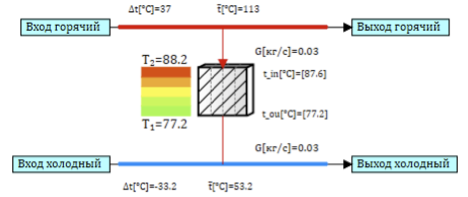
Gambar 2. Model sel penukar panas.

Model penukar panas tubular mudah disesuaikan. Anda hanya dapat mengubah satu parameter - jumlah bagian di sepanjang pipa dan lihat hasil perhitungan untuk partisi yang berbeda. Kami akan menghitung beberapa opsi, mulai dari membagi menjadi 5 titik panjang (Gbr. 3) dan panjang hingga 100 poin (Gbr. 4).

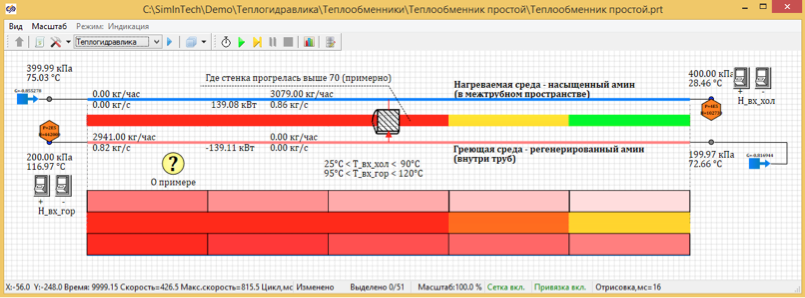
Gambar 3. Distribusi suhu stasioner dari 5 titik desain.

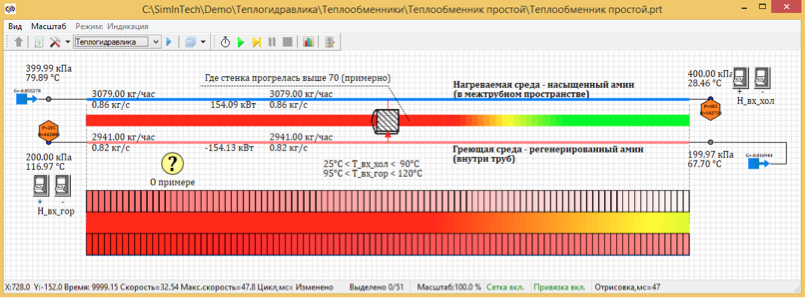
Gambar 4. Distribusi suhu stasioner 100 titik desain.

Sebagai hasil perhitungan, ternyata suhu tunak ketika dibagi 100 poin adalah 67,7 derajat. Dan ketika dibagi menjadi 5 titik terhitung, suhunya 72, 66 derajat C.

Juga, kecepatan perhitungan relatif terhadap waktu nyata ditampilkan di bagian bawah jendela.
Mari kita lihat bagaimana suhu kondisi-mapan dan kecepatan perhitungan berubah tergantung pada jumlah titik desain. Perbedaan suhu kondisi mapan dalam perhitungan dengan jumlah sel perhitungan yang berbeda dapat digunakan untuk menilai akurasi hasil.

Tabel 1. Ketergantungan suhu dan kecepatan perhitungan pada jumlah titik desain di sepanjang penukar panas.

Menganalisis tabel ini, kita bisa menarik kesimpulan berikut:

• Kecepatan perhitungan menurun secara proporsional dengan jumlah titik desain dalam model penukar panas.
• Perubahan dalam akurasi perhitungan terjadi secara eksponensial. Ketika jumlah poin meningkat, penyempurnaan pada setiap kenaikan berikutnya berkurang.

Dalam kasus penukar panas pelat dengan pembawa panas cross-flow, seperti pada Gambar 1, penciptaan model yang setara dari sel desain dasar sedikit rumit. Kita perlu menghubungkan sel-sel sedemikian rupa untuk mengatur aliran silang. Untuk 4 sel, rangkaian akan terlihat seperti yang ditunjukkan pada Gambar 5.

Aliran pendingin dibagi menjadi dua saluran di sepanjang cabang panas dan dingin, saluran akan dihubungkan melalui struktur termal, sehingga ketika melewati saluran, pendingin bertukar panas dengan saluran yang berbeda. Mensimulasikan aliran silang, pembawa panas mengalir dari kiri ke kanan (lihat Gambar. 5) di setiap saluran, secara berurutan bertukar panas dengan saluran pembawa panas dingin, yang bergerak dari bawah ke atas (lihat Gambar. 5). Titik terpanas adalah di sudut kiri atas, karena pembawa panas bertukar panas dengan pendingin yang sudah dipanaskan dari saluran dingin. Dan yang terdingin di kanan bawah, di mana pendingin dingin bertukar panas dengan pendingin panas yang sudah didinginkan di bagian pertama.

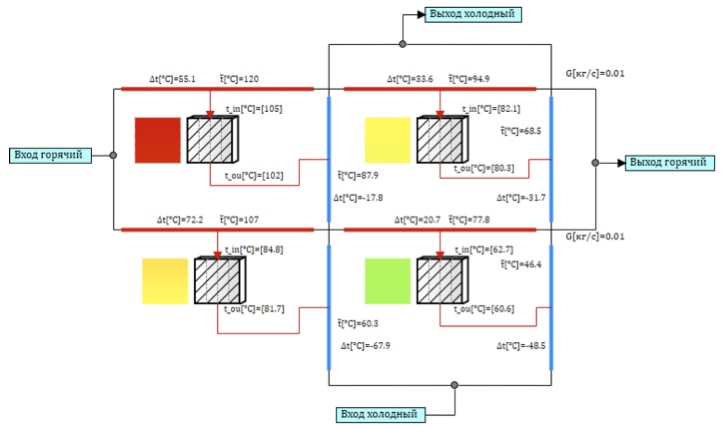
Gambar 5. Model cross-flow dari 4 sel desain.

Model seperti itu untuk penukar panas pelat tidak memperhitungkan perpindahan panas antar sel karena konduktivitas termal dan tidak memperhitungkan pencampuran pendingin, karena setiap saluran diisolasi.

Tetapi dalam kasus kami, batasan terakhir tidak mengurangi akurasi, karena dalam desain penukar panas, membran bergelombang membagi aliran menjadi banyak saluran terisolasi di sepanjang pendingin (lihat Gambar 1). Mari kita lihat apa yang terjadi dengan keakuratan perhitungan ketika memodelkan penukar panas piring dengan peningkatan jumlah sel desain.

Untuk analisis akurasi, kami menggunakan dua opsi untuk membagi penukar panas ke dalam sel desain:

1. Setiap sel persegi berisi dua hidrolik (aliran dingin dan panas) dan satu elemen termal. (lihat gambar 5)
2. Setiap sel persegi berisi enam elemen hidrolik (tiga bagian dalam aliran panas dan dingin) dan tiga elemen termal.

Dalam kasus terakhir, kami menggunakan dua jenis koneksi:

• arus balik aliran dingin dan panas;
• terkait aliran dingin dan panas.

Arus yang datang meningkatkan efisiensi dibandingkan dengan cross-flow, dan arus yang terkait berkurang. Dengan sejumlah besar sel, aliran rata-rata terjadi dan semuanya menjadi dekat dengan aliran transversal yang sebenarnya di sekitarnya (lihat Gambar 6).

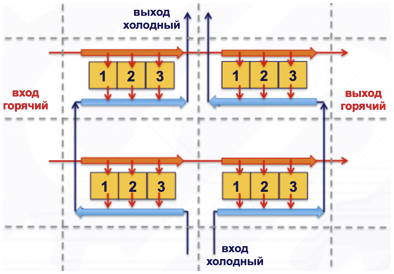
Gambar 6. Model cross-flow empat sel dengan 3 elemen.

Gambar 7 menunjukkan hasil distribusi suhu stasioner kondisi-mapan dalam penukar panas ketika memasok udara pada suhu 150 ° C di sepanjang jalur panas, dan 21 ° C di sepanjang garis dingin, untuk berbagai opsi untuk mempartisi model. Warna dan angka pada sel mencerminkan suhu rata-rata dinding dalam sel.

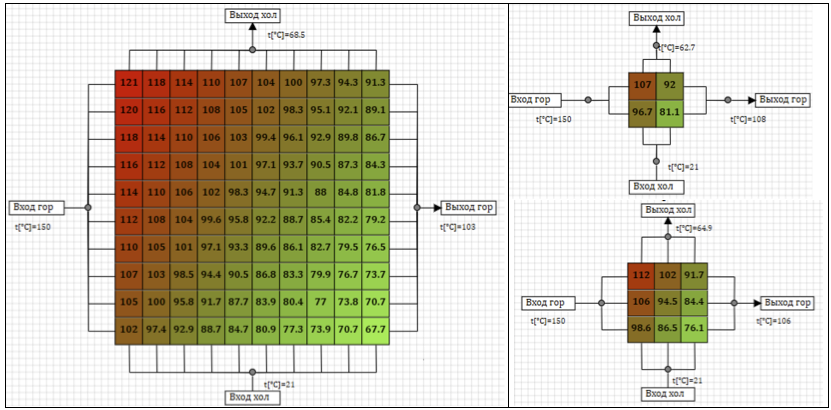
Gambar 7. Temperatur steady-state untuk berbagai skema perhitungan.

Tabel 2 menunjukkan suhu tunak udara panas setelah penukar panas, tergantung pada partisi model penukar panas ke dalam sel.

Tabel 2. Ketergantungan suhu pada jumlah sel desain dalam penukar panas.

Dengan peningkatan jumlah sel komputasi dalam model, suhu tunak akhir meningkat. Perbedaan antara suhu kondisi-mapan pada partisi yang berbeda dapat dianggap sebagai indikator akurasi perhitungan. Terlihat bahwa dengan peningkatan jumlah sel perhitungan, suhu cenderung ke batas, dan peningkatan keakuratan tidak sebanding dengan jumlah titik perhitungan.

Muncul pertanyaan, tetapi keakuratan model apa yang kita butuhkan?

Jawaban untuk pertanyaan ini tergantung pada tujuan model kami. Karena artikel ini adalah tentang desain berorientasi model, kami membuat model untuk menyetel sistem kontrol. Ini berarti bahwa keakuratan model harus sebanding dengan keakuratan sensor yang digunakan dalam sistem.

Dalam kasus kami, suhu diukur dengan termokopel, di mana akurasi adalah ± 2,5 ° C. Akurasi apa pun yang lebih tinggi untuk tujuan penyetelan sistem kontrol tidak berguna, sistem kontrol kami yang sesungguhnya hanya "tidak akan melihatnya." Jadi, jika kita mengasumsikan bahwa suhu batas dengan jumlah partisi yang tidak terbatas adalah 70 ° C, maka model yang memberi kita lebih dari 67,5 ° C akan memiliki akurasi yang cukup. Semua model dengan 3 poin dalam sel perhitungan dan model lebih besar dari 5x5 dengan satu poin di dalam sel. (Disorot hijau dalam tabel 2)

. (. . 8)


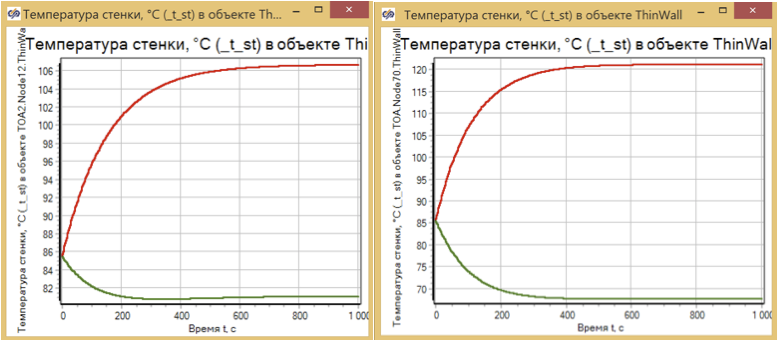
8. . 22 1010.

, , , .

, , 20 150 °, , , 10 – 20 .

, , , , , .

, , . 9 . , , , .

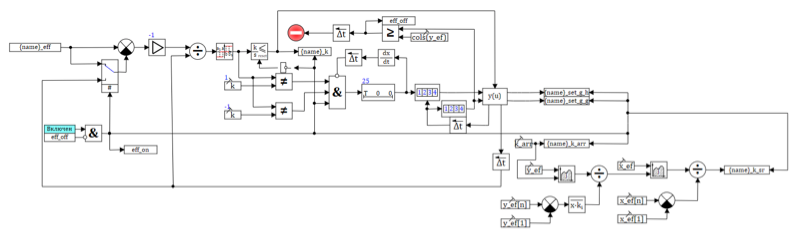
9. .

a . , ( ) . , 0.492 0.655

0.6, , , .

– :

:
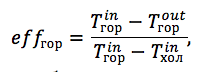
eff – ;
T ⁱⁿ – ;
T ^out – ;
T ⁱⁿ – .

3 .

3. %

. , , , , .

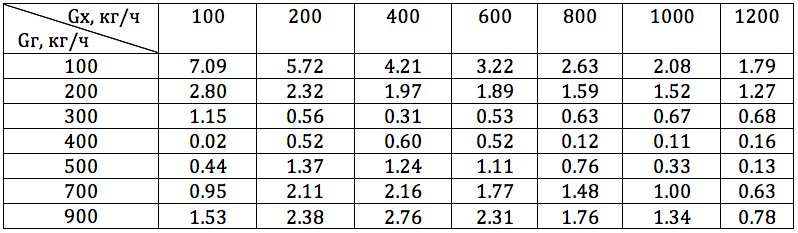
, 10 .

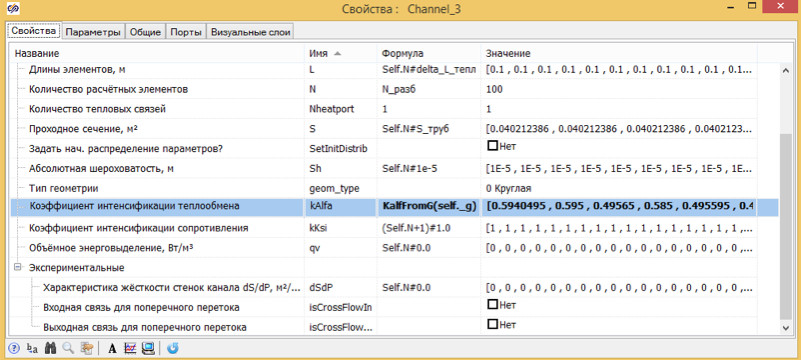
10. .

Kesimpulan

• - .
  
• .
  
• .
  
• - !

. .